Entrelazamiento cuántico

Parte de una serie de artículos sobre
Mecánica cuántica
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Ecuación de Schrödinger
Introducción Glosario Historia
Fondo Mecánica clásica Antigua teoría cuántica Notación de corchetes Hamiltoniano Interferencia
Fundamentos Complementariedad Decoherencia Enredo Nivel de energía Medición No localidad Número cuántico Estado Superposición Simetría Túnel Incertidumbre Función de onda Colapsar
Experimentos Desigualdad de Bell Desigualdad de CHSH Davisson-Germer Doble rendija Elitzur–Vaidman Franck-Hertz Desigualdad de Leggett Desigualdad de Leggett-Garg Mach–Zehnder Corchete Borrador cuántico Elección retrasada El gato de Schrödinger Stern–Gerlach La elección retrasada de Wheeler
Formulaciones Descripción general Heisenberg Interacción Matriz Espacio de fases Schrödinger Suma de historias (integral de trayectoria)
Ecuaciones Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Superdeterminism Many-worlds Objective-collapse Quantum logic Relational Transactional Von Neumann–Wigner
Advanced topics Relativistic quantum mechanics Quantum field theory Quantum information science Quantum computing Quantum chaos EPR paradox Density matrix Scattering theory Quantum statistical mechanics Quantum machine learning
Scientists Aharonov Bell Bethe Blackett Bloch Bohm Bohr Born Bose de Broglie Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Lamb Landau Laue Moseley Millikan Onnes Pauli Planck Rabi Raman Rydberg Schrödinger Simmons Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

El entrelazamiento cuántico es el fenómeno por el cual un grupo de partículas se genera, interactúa o comparte proximidad espacial de tal manera que el estado cuántico de cada partícula del grupo no puede describirse independientemente del estado de las demás, incluso cuando las partículas están separadas por una gran distancia. El tema del entrelazamiento cuántico está en el centro de la disparidad entre la física clásica y la cuántica : el entrelazamiento es una característica primaria de la mecánica cuántica que no está presente en la mecánica clásica. ^[1]

En algunos casos, se puede comprobar que las mediciones de propiedades físicas como la posición , el momento , el espín y la polarización realizadas en partículas entrelazadas están perfectamente correlacionadas . Por ejemplo, si se genera un par de partículas entrelazadas de modo que se sepa que su espín total es cero, y se descubre que una partícula tiene un espín en el sentido de las agujas del reloj en un primer eje, se descubre que el espín de la otra partícula, medido en el mismo eje, es en sentido contrario a las agujas del reloj. Sin embargo, este comportamiento da lugar a efectos aparentemente paradójicos : cualquier medición de las propiedades de una partícula da como resultado un colapso aparente e irreversible de la función de onda de esa partícula y cambia el estado cuántico original. Con partículas entrelazadas, dichas mediciones afectan al sistema entrelazado en su conjunto.

Tales fenómenos fueron el tema de un artículo de 1935 de Albert Einstein , Boris Podolsky y Nathan Rosen , ^[2] y varios artículos de Erwin Schrödinger poco después, ^{[3] [4]} describiendo lo que llegó a conocerse como la paradoja EPR . Einstein y otros consideraron que tal comportamiento era imposible, ya que violaba la visión del realismo local de la causalidad (Einstein se refirió a él como " acción fantasmal a distancia ") ^[5] y argumentaron que la formulación aceptada de la mecánica cuántica debe, por lo tanto, ser incompleta.

Sin embargo, más tarde, las predicciones contraintuitivas de la mecánica cuántica se verificaron ^{[6] [7] [8]} en pruebas en las que se midieron la polarización o el giro de partículas entrelazadas en lugares separados, violando estadísticamente la desigualdad de Bell . En pruebas anteriores, no se podía descartar que el resultado en un punto pudiera haberse transmitido sutilmente al punto remoto, afectando el resultado en el segundo lugar. ^[8] Sin embargo, desde entonces se han realizado las llamadas pruebas de Bell "sin lagunas" en las que los lugares estaban lo suficientemente separados como para que las comunicaciones a la velocidad de la luz hubieran tardado más (en un caso, 10.000 veces más) que el intervalo entre las mediciones. ^{[7] [6]}

Según algunas interpretaciones de la mecánica cuántica , el efecto de una medición se produce instantáneamente. Otras interpretaciones que no reconocen el colapso de la función de onda cuestionan que exista algún "efecto". Sin embargo, todas las interpretaciones coinciden en que el entrelazamiento produce correlación entre las mediciones y que la información mutua entre las partículas entrelazadas puede aprovecharse, pero que cualquier transmisión de información a velocidades superiores a la de la luz es imposible. ^{[9] [10]} Por lo tanto, a pesar del pensamiento popular en sentido contrario, el entrelazamiento cuántico no puede utilizarse para la comunicación a velocidades superiores a la de la luz . ^[11]

El entrelazamiento cuántico se ha demostrado experimentalmente con fotones , ^{[12] [13]} electrones , ^{[14] [15]} quarks top, ^[16] moléculas ^[17] e incluso pequeños diamantes. ^[18] El uso del entrelazamiento en la comunicación , la computación y el radar cuántico es un área activa de investigación y desarrollo.

En 1935, Albert Einstein , Boris Podolsky y Nathan Rosen publicaron un artículo sobre las predicciones contraintuitivas que la mecánica cuántica hace para pares de objetos preparados juntos de una manera particular. ^[2] En este estudio, los tres formularon la paradoja de Einstein-Podolsky-Rosen (paradoja EPR), un experimento mental que intentó demostrar que "la descripción mecánico-cuántica de la realidad física dada por las funciones de onda no es completa". ^[2] Sin embargo, los tres científicos no acuñaron la palabra entrelazamiento , ni generalizaron las propiedades especiales del estado cuántico que consideraron. Después del artículo EPR, Erwin Schrödinger escribió una carta a Einstein en alemán en la que usó la palabra Verschränkung (traducida por él mismo como entrelazamiento ) "para describir las correlaciones entre dos partículas que interactúan y luego se separan, como en el experimento EPR". ^[19] Sin embargo, Schrödinger había discutido el fenómeno ya en 1932. ^[20]

Schrödinger publicó poco después un artículo seminal que definía y discutía la noción de "entrelazamiento". En el artículo, reconoció la importancia del concepto y afirmó: ^[3] "No llamaría [entrelazamiento] uno sino más bien el rasgo característico de la mecánica cuántica, el que impone su total desviación de las líneas clásicas de pensamiento". Al igual que Einstein, Schrödinger no estaba satisfecho con el concepto de entrelazamiento, porque parecía violar el límite de velocidad en la transmisión de información implícito en la teoría de la relatividad . ^[21] Einstein más tarde ridiculizó el entrelazamiento como " spukhafte Fernwirkung " ^[22] o " acción fantasmal a distancia ".

El artículo de EPR generó un interés significativo entre los físicos, lo que inspiró mucho debate sobre los fundamentos de la mecánica cuántica y la interpretación de Bohm en particular, pero produjo relativamente pocos trabajos publicados. A pesar del interés, el punto débil del argumento de EPR no se descubrió hasta 1964, cuando John Stewart Bell demostró que uno de sus supuestos clave, el principio de localidad , aplicado al tipo de interpretación de variables ocultas que esperaba EPR, era matemáticamente incompatible con las predicciones de la teoría cuántica.

En concreto, Bell demostró un límite superior, visto en la desigualdad de Bell , con respecto a la fuerza de las correlaciones que se pueden producir en cualquier teoría que obedezca al realismo local , y mostró que la teoría cuántica predice violaciones de este límite para ciertos sistemas entrelazados. ^[23] Su desigualdad es experimentalmente comprobable, y ha habido numerosos experimentos relevantes , empezando por el trabajo pionero de Stuart Freedman y John Clauser en 1972 ^[24] y los experimentos de Alain Aspect en 1982. ^[25]

Un avance experimental temprano se debió a Carl Kocher, ^{[12] [13]} quien ya en 1967 presentó un aparato en el que se demostró que dos fotones emitidos sucesivamente desde un átomo de calcio estaban entrelazados: el primer caso de luz visible entrelazada. Los dos fotones pasaron por polarizadores paralelos colocados diametralmente con mayor probabilidad que la predicha clásicamente, pero con correlaciones que concordaban cuantitativamente con los cálculos de la mecánica cuántica. También demostró que la correlación variaba como el coseno al cuadrado del ángulo entre los ajustes del polarizador ^[13] y disminuía exponencialmente con el desfase temporal entre los fotones emitidos. ^[26] El aparato de Kocher, equipado con mejores polarizadores, fue utilizado por Freedman y Clauser, quienes pudieron confirmar la dependencia del coseno al cuadrado y usarla para demostrar una violación de la desigualdad de Bell para un conjunto de ángulos fijos. ^[24] Todos estos experimentos han demostrado concordancia con la mecánica cuántica en lugar del principio de realismo local.

Durante décadas, cada uno de ellos había dejado abierta al menos una laguna por la que era posible cuestionar la validez de los resultados. Sin embargo, en 2015 se realizó un experimento que simultáneamente cerró las lagunas de detección y de localidad, y fue anunciado como "libre de lagunas"; este experimento descartó con certeza una gran clase de teorías de realismo local. ^[27] Aspect escribe que "... no se puede decir que ningún experimento... esté totalmente libre de lagunas", pero dice que los experimentos "eliminan las últimas dudas de que deberíamos renunciar" a las variables ocultas locales, y se refiere a ejemplos de lagunas restantes como "inverosímiles" y "ajenos a la forma habitual de razonamiento en física". ^[28]

El trabajo de Bell planteó la posibilidad de utilizar estas correlaciones superfuertes como recurso para la comunicación. Esto condujo al descubrimiento en 1984 de los protocolos de distribución de claves cuánticas , los más famosos BB84 de Charles H. Bennett y Gilles Brassard ^[29] y E91 de Artur Ekert ^[30] . Aunque BB84 no utiliza el entrelazamiento, el protocolo de Ekert utiliza la violación de una desigualdad de Bell como prueba de seguridad.

En 2022, el Premio Nobel de Física fue otorgado a Alain Aspect , John Clauser y Anton Zeilinger "por experimentos con fotones entrelazados, estableciendo la violación de las desigualdades de Bell y siendo pioneros en la ciencia de la información cuántica". ^[31]

Un sistema entrelazado puede definirse como aquel cuyo estado cuántico no puede factorizarse como un producto de los estados de sus constituyentes locales; es decir, no son partículas individuales sino un todo inseparable. En el entrelazamiento, un constituyente no puede describirse completamente sin considerar el otro u otros. El estado de un sistema compuesto siempre se puede expresar como una suma o superposición de productos de estados de constituyentes locales; está entrelazado si esta suma no puede escribirse como un único término de producto.

Los sistemas cuánticos pueden enredarse mediante diversos tipos de interacciones. Para conocer algunas formas en las que se puede lograr el entrelazamiento con fines experimentales, consulte la sección sobre métodos que aparece a continuación. El entrelazamiento se rompe cuando las partículas entrelazadas pierden su coherencia mediante la interacción con el entorno; por ejemplo, cuando se realiza una medición. ^[32]

Como ejemplo de entrelazamiento: una partícula subatómica se desintegra en un par entrelazado de otras partículas. Los eventos de desintegración obedecen a las diversas leyes de conservación y, como resultado, los resultados de la medición de una partícula hija deben estar altamente correlacionados con los resultados de la medición de la otra partícula hija (de modo que los momentos totales, los momentos angulares, la energía, etc. permanezcan aproximadamente iguales antes y después de este proceso). Por ejemplo, una partícula de espín cero podría desintegrarse en un par de partículas de espín 1/2. Dado que el espín total antes y después de esta desintegración debe ser cero (conservación del momento angular), siempre que se mida que la primera partícula tiene espín hacia arriba en algún eje, la otra, cuando se mide en el mismo eje, siempre tiene espín hacia abajo . (Esto se llama el caso de espín anticorrelacionado; y si las probabilidades previas para medir cada espín son iguales, se dice que el par está en el estado singlete ).

El resultado anterior puede o no ser percibido como sorprendente. Un sistema clásico mostraría la misma propiedad, y ciertamente se requeriría una teoría de variable oculta para hacerlo, basada en la conservación del momento angular tanto en la mecánica clásica como en la cuántica. La diferencia es que un sistema clásico tiene valores definidos para todos los observables a lo largo del tiempo, mientras que el sistema cuántico no los tiene. En un sentido que se discutirá más adelante, el sistema cuántico considerado aquí parece adquirir una distribución de probabilidad para el resultado de una medición del espín a lo largo de cualquier eje de la otra partícula al medir la primera partícula. Esta distribución de probabilidad es en general diferente de lo que sería sin la medición de la primera partícula. Esto ciertamente puede percibirse como sorprendente en el caso de partículas entrelazadas separadas espacialmente.

La paradoja es que una medición realizada en cualquiera de las partículas aparentemente colapsa el estado de todo el sistema entrelazado, y lo hace instantáneamente, antes de que cualquier información sobre el resultado de la medición pudiera haber sido comunicada a la otra partícula (suponiendo que la información no puede viajar más rápido que la luz ) y, por lo tanto, aseguró el resultado "adecuado" de la medición de la otra parte del par entrelazado. En la interpretación de Copenhague , el resultado de una medición de espín en una de las partículas es un colapso (de la función de onda) en un estado en el que cada partícula tiene un espín definido (hacia arriba o hacia abajo) a lo largo del eje de medición. El resultado se considera aleatorio, y cada posibilidad tiene una probabilidad del 50%. Sin embargo, si ambos espines se miden a lo largo del mismo eje, se descubre que están anticorrelacionados. Esto significa que el resultado aleatorio de la medición realizada en una partícula parece haber sido transmitido a la otra, de modo que puede hacer la "elección correcta" cuando también se mide. ^[33]

La distancia y el momento de las mediciones se pueden elegir de modo que el intervalo entre las dos mediciones sea espacial , por lo tanto, cualquier efecto causal que conecte los eventos tendría que viajar más rápido que la luz. De acuerdo con los principios de la relatividad especial , no es posible que ninguna información viaje entre dos eventos de medición de este tipo. Ni siquiera es posible decir cuál de las mediciones se produjo primero. Para dos eventos separados espacialmente x ₁ y x ₂ hay marcos inerciales en los que x ₁ es primero y otros en los que x ₂ es primero. Por lo tanto, la correlación entre las dos mediciones no se puede explicar como una medición que determina a la otra: diferentes observadores estarían en desacuerdo sobre el papel de la causa y el efecto.

(De hecho, pueden surgir paradojas similares incluso sin entrelazamiento: la posición de una sola partícula está dispersa en el espacio, y dos detectores muy separados que intentan detectar la partícula en dos lugares diferentes deben alcanzar instantáneamente una correlación apropiada, de modo que no puedan detectar ambos la partícula).

Una posible solución a la paradoja es suponer que la teoría cuántica es incompleta y que el resultado de las mediciones depende de "variables ocultas" predeterminadas. ^[34] El estado de las partículas que se miden contiene algunas variables ocultas , cuyos valores determinan efectivamente, desde el momento de la separación, cuáles serán los resultados de las mediciones de espín. Esto significaría que cada partícula lleva consigo toda la información necesaria y no es necesario transmitir nada de una partícula a la otra en el momento de la medición. Einstein y otros (véase la sección anterior) creyeron originalmente que esta era la única forma de salir de la paradoja y que la descripción mecánica cuántica aceptada (con un resultado de medición aleatorio) debe ser incompleta.

Sin embargo, las teorías de variables ocultas locales fallan cuando se consideran mediciones del espín de partículas entrelazadas a lo largo de diferentes ejes. Si se realiza una gran cantidad de pares de tales mediciones (en una gran cantidad de pares de partículas entrelazadas), entonces estadísticamente, si la visión realista local o de variables ocultas fuera correcta, los resultados siempre satisfarían la desigualdad de Bell . Una serie de experimentos han demostrado en la práctica que la desigualdad de Bell no se satisface. Sin embargo, antes de 2015, todos estos experimentos tenían problemas de lagunas que fueron considerados los más importantes por la comunidad de físicos. ^{[35] [36]} Cuando las mediciones de las partículas entrelazadas se realizan en marcos de referencia relativistas móviles , en los que cada medición (en su propio marco de tiempo relativista) ocurre antes que la otra, los resultados de la medición permanecen correlacionados. ^{[37] [38]}

La cuestión fundamental sobre la medición del espín a lo largo de diferentes ejes es que estas mediciones no pueden tener valores definidos al mismo tiempo: son incompatibles en el sentido de que la precisión simultánea máxima de estas mediciones está limitada por el principio de incertidumbre . Esto es contrario a lo que se encuentra en la física clásica, donde cualquier número de propiedades se puede medir simultáneamente con una precisión arbitraria. Se ha demostrado matemáticamente que las mediciones compatibles no pueden mostrar correlaciones que violen la desigualdad de Bell ^[39] y, por lo tanto, el entrelazamiento es un fenómeno fundamentalmente no clásico.

El primer experimento que verificó la acción fantasmal de Einstein a distancia (entrelazamiento) fue corroborado con éxito en un laboratorio por Chien-Shiung Wu y su colega I. Shaknov en 1949, y fue publicado el día de Año Nuevo de 1950. El resultado demostró específicamente las correlaciones cuánticas de un par de fotones. ^[40] En experimentos de 2012 y 2013, se creó una correlación de polarización entre fotones que nunca coexistieron en el tiempo. ^{[41] [42]} Los autores afirmaron que este resultado se logró mediante el intercambio de entrelazamiento entre dos pares de fotones entrelazados después de medir la polarización de un fotón del par inicial, y que demuestra que la no localidad cuántica se aplica no solo al espacio sino también al tiempo.

En tres experimentos independientes realizados en 2013, se demostró que los estados cuánticos separables comunicados clásicamente pueden utilizarse para transportar estados entrelazados. ^[43] La primera prueba de Bell sin lagunas fue realizada por Ronald Hanson de la Universidad Tecnológica de Delft en 2015, confirmando la violación de la desigualdad de Bell. ^[44]

En agosto de 2014, la investigadora brasileña Gabriela Barreto Lemos y su equipo lograron "tomar fotografías" de objetos utilizando fotones que no habían interactuado con los sujetos, pero que estaban entrelazados con fotones que sí interactuaban con dichos objetos. Lemos, de la Universidad de Viena, confía en que esta nueva técnica de obtención de imágenes cuánticas pueda encontrar aplicación allí donde la obtención de imágenes con poca luz sea imprescindible, en campos como la obtención de imágenes biológicas o médicas. ^[45]

Desde 2016, varias empresas, por ejemplo IBM y Microsoft, han creado computadoras cuánticas que permitieron a los desarrolladores y entusiastas de la tecnología experimentar libremente con conceptos de la mecánica cuántica, incluido el entrelazamiento cuántico. ^[46]

Existe un conflicto fundamental, conocido como el problema del tiempo , entre la forma en que se utiliza el concepto de tiempo en la mecánica cuántica y el papel que desempeña en la relatividad general . En las teorías cuánticas estándar, el tiempo actúa como un fondo independiente a través del cual evolucionan los estados, y el operador hamiltoniano actúa como generador de traducciones infinitesimales de estados cuánticos a través del tiempo. ^[47]

En cambio, la relatividad general trata el tiempo como una variable dinámica que se relaciona directamente con la materia y, además, requiere que la restricción hamiltoniana desaparezca. En la relatividad general cuantizada , la versión cuántica de la restricción hamiltoniana que utiliza variables métricas, conduce a la ecuación de Wheeler-DeWitt :

donde es la restricción hamiltoniana y representa la función de onda del universo . El operador actúa sobre el espacio de Hilbert de funciones de onda, pero no es el mismo espacio de Hilbert que en el caso no relativista. Este hamiltoniano ya no determina la evolución del sistema porque la ecuación de Schrödinger : , deja de ser válida. Esta propiedad se conoce como atemporalidad. Se han realizado varios intentos de incorporar el tiempo en un marco completamente cuántico, comenzando con el mecanismo de Page y Wootters y otras propuestas posteriores. ^{[48] [49]}${\displaystyle {\hat {H}}(x)}$${\displaystyle |\psi \rangle }$${\displaystyle {\hat {H}}}$${\displaystyle {\hat {H}}|\psi \rangle =i\hbar {\partial \over {\partial t}}|\psi \rangle }$

También se propuso que el surgimiento del tiempo surge de correlaciones cuánticas entre un sistema en evolución y un sistema de reloj cuántico de referencia; se introduce el concepto de entrelazamiento sistema-tiempo como cuantificador de la evolución distinguible real sufrida por el sistema. ^{[50] [51] [52] [53]}

Basándose en la correspondencia AdS/CFT , Mark Van Raamsdonk sugirió que el espacio-tiempo surge como un fenómeno emergente de los grados cuánticos de libertad que están entrelazados y viven en el límite del espacio-tiempo. ^[54] La gravedad inducida puede surgir de la primera ley del entrelazamiento. ^{[55] [56]}

En los medios de comunicación y en la ciencia popular, la no localidad cuántica se presenta a menudo como equivalente al entrelazamiento. Si bien esto es cierto para los estados cuánticos bipartitos puros, en general el entrelazamiento solo es necesario para correlaciones no locales, pero existen estados entrelazados mixtos que no producen tales correlaciones. ^[57] Un ejemplo bien conocido son los estados de Werner que están entrelazados para ciertos valores de , pero siempre se pueden describir utilizando variables ocultas locales. ^[58] Además, se demostró que, para un número arbitrario de partículas, existen estados que están genuinamente entrelazados pero admiten un modelo local. ^[59]${\displaystyle p_{sym}}$

Las pruebas mencionadas sobre la existencia de modelos locales suponen que sólo hay una copia del estado cuántico disponible a la vez. Si se permite que las partículas realicen mediciones locales en muchas copias de dichos estados, muchos estados aparentemente locales (por ejemplo, los estados de Werner de los cúbits) ya no pueden describirse mediante un modelo local. Esto es, en particular, cierto para todos los estados destilables . Sin embargo, sigue siendo una pregunta abierta si todos los estados entrelazados se vuelven no locales dada una cantidad suficiente de copias. ^[60]

El entrelazamiento de un estado compartido por dos partículas es necesario, pero no suficiente, para que ese estado sea no local. El entrelazamiento se considera más comúnmente como un concepto algebraico, conocido por ser un prerrequisito para la no localidad, así como para la teletransportación cuántica y la codificación superdensa , mientras que la no localidad se define de acuerdo con las estadísticas experimentales y está mucho más relacionada con los fundamentos e interpretaciones de la mecánica cuántica . ^[61]

Las siguientes subsecciones están dirigidas a aquellos con un buen conocimiento práctico de la descripción matemática formal de la mecánica cuántica, incluida la familiaridad con el formalismo y el marco teórico desarrollado en los artículos: notación bra-ket y formulación matemática de la mecánica cuántica .

Consideremos dos sistemas cuánticos arbitrarios A y B , con respectivos espacios de Hilbert H _A y H _B . El espacio de Hilbert del sistema compuesto es el producto tensorial

${\displaystyle H_{A}\otimes H_{B}.}$

Si el primer sistema está en estado y el segundo en estado , el estado del sistema compuesto es${\displaystyle |\psi \rangle _{A}}$${\displaystyle |\phi \rangle _{B}}$

${\displaystyle |\psi \rangle _{A}\otimes |\phi \rangle _{B}.}$

Los estados del sistema compuesto que pueden representarse de esta forma se denominan estados separables o estados producto .

No todos los estados son separables (y por lo tanto, estados producto). Fije una base para H _A y una base para H _B . El estado más general en H _A ⊗ H _B es de la forma${\displaystyle \{|i\rangle _{A}\}}$${\displaystyle \{|j\rangle _{B}\}}$

${\displaystyle |\psi \rangle _{AB}=\sum _{i,j}c_{ij}|i\rangle _{A}\otimes |j\rangle _{B}}$.

Este estado es separable si existen vectores tales que se obtiene y Es inseparable si para cualquier vector al menos para un par de coordenadas tenemos Si un estado es inseparable, se denomina "estado entrelazado".${\displaystyle [c_{i}^{A}],[c_{j}^{B}]}$${\displaystyle c_{ij}=c_{i}^{A}c_{j}^{B},}$${\textstyle |\psi \rangle _{A}=\sum _{i}c_{i}^{A}|i\rangle _{A}}$${\textstyle |\phi \rangle _{B}=\sum _{j}c_{j}^{B}|j\rangle _{B}.}$${\displaystyle [c_{i}^{A}],[c_{j}^{B}]}$${\displaystyle c_{i}^{A},c_{j}^{B}}$${\displaystyle c_{ij}\neq c_{i}^{A}c_{j}^{B}.}$

Por ejemplo, dados dos vectores base de H _A y dos vectores base de H _B , el siguiente es un estado entrelazado:${\displaystyle \{|0\rangle _{A},|1\rangle _{A}\}}$${\displaystyle \{|0\rangle _{B},|1\rangle _{B}\}}$

${\displaystyle {\tfrac {1}{\sqrt {2}}}\left(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}\right).}$

Si el sistema compuesto está en este estado, es imposible atribuir al sistema A o al sistema B un estado puro definido . Otra forma de decir esto es que mientras que la entropía de von Neumann de todo el estado es cero (como lo es para cualquier estado puro), la entropía de los subsistemas es mayor que cero. En este sentido, los sistemas están "entrelazados". Esto tiene ramificaciones empíricas específicas para la interferometría. ^[62] El ejemplo anterior es uno de los cuatro estados de Bell , que son estados puros (máximamente) entrelazados (estados puros del espacio H _A ⊗ H _B , pero que no se pueden separar en estados puros de cada H _A y H _B ).

Ahora supongamos que Alice es un observador del sistema A y Bob es un observador del sistema B. Si en el estado entrelazado dado anteriormente Alice realiza una medición en la base propia de A , hay dos resultados posibles, que ocurren con igual probabilidad: ^[63]${\displaystyle \{|0\rangle ,|1\rangle \}}$

1. Alice mide 0 y el estado del sistema colapsa a .${\displaystyle |0\rangle _{A}|1\rangle _{B}}$
2. Alice mide 1 y el estado del sistema colapsa a .${\displaystyle |1\rangle _{A}|0\rangle _{B}}$

Si ocurre lo primero, entonces cualquier medición posterior realizada por Bob, sobre la misma base, siempre devolverá 1. Si ocurre lo segundo (Alice mide 1), entonces la medición de Bob devolverá 0 con certeza. Por lo tanto, el sistema B ha sido alterado por Alice al realizar una medición local en el sistema A. Esto sigue siendo cierto incluso si los sistemas A y B están separados espacialmente. Esta es la base de la paradoja EPR.

El resultado de la medición de Alice es aleatorio. Alice no puede decidir en qué estado colapsar el sistema compuesto y, por lo tanto, no puede transmitir información a Bob actuando sobre su sistema. Por lo tanto, en este esquema particular se preserva la causalidad. Para el argumento general, véase el teorema de no comunicación .

Como se mencionó anteriormente, el estado de un sistema cuántico se da mediante un vector unitario en un espacio de Hilbert. De manera más general, si se tiene menos información sobre el sistema, se lo llama "conjunto" y se lo describe mediante una matriz de densidad , que es una matriz semidefinida positiva , o una clase de traza cuando el espacio de estados es de dimensión infinita y tiene traza 1. Nuevamente, por el teorema espectral , dicha matriz toma la forma general:

${\displaystyle \rho =\sum _{i}w_{i}|\alpha _{i}\rangle \langle \alpha _{i}|,}$

donde w _i son probabilidades de valor positivo (suman 1), los vectores α _i son vectores unitarios y, en el caso de dimensión infinita, tomaríamos la clausura de tales estados en la norma de traza. Podemos interpretar ρ como la representación de un conjunto donde es la proporción del conjunto cuyos estados son . Cuando un estado mixto tiene rango 1, describe por tanto un "conjunto puro". Cuando hay menos que información total sobre el estado de un sistema cuántico, necesitamos matrices de densidad para representar el estado.${\displaystyle w_{i}}$${\displaystyle |\alpha _{i}\rangle }$

Experimentalmente, un conjunto mixto podría realizarse de la siguiente manera. Consideremos un aparato de "caja negra" que lanza electrones hacia un observador. Los espacios de Hilbert de los electrones son idénticos . El aparato podría producir electrones que estén todos en el mismo estado; en este caso, los electrones recibidos por el observador son entonces un conjunto puro. Sin embargo, el aparato podría producir electrones en diferentes estados. Por ejemplo, podría producir dos poblaciones de electrones: una con un estado con espines alineados en la dirección z positiva , y la otra con un estado con espines alineados en la dirección y negativa . Generalmente, este es un conjunto mixto, ya que puede haber cualquier número de poblaciones, cada una correspondiente a un estado diferente.${\displaystyle |\mathbf {z} +\rangle }$${\displaystyle |\mathbf {y} -\rangle }$

Siguiendo la definición anterior, para un sistema compuesto bipartito, los estados mixtos son simplemente matrices de densidad en H _A ⊗ H _B . Es decir, tiene la forma general

${\displaystyle \rho =\sum _{i}w_{i}\left[\sum _{j}{\bar {c}}_{ij}(|\alpha _{ij}\rangle \otimes |\beta _{ij}\rangle )\right]\left[\sum _{k}c_{ik}(\langle \alpha _{ik}|\otimes \langle \beta _{ik}|)\right]}$

donde w _i son probabilidades con valores positivos, y los vectores son vectores unitarios. Esto es autoadjunto y positivo y tiene traza 1.${\textstyle \sum _{j}|c_{ij}|^{2}=1}$

Extendiendo la definición de separabilidad del caso puro, decimos que un estado mixto es separable si puede escribirse como ^{[64] : 131–132}

${\displaystyle \rho =\sum _{i}w_{i}\rho _{i}^{A}\otimes \rho _{i}^{B},}$

donde w _i son probabilidades con valores positivos y los ' y ' son en sí mismos estados mixtos (operadores de densidad) en los subsistemas A y B respectivamente. En otras palabras, un estado es separable si es una distribución de probabilidad sobre estados no correlacionados, o estados producto. Al escribir las matrices de densidad como sumas de conjuntos puros y expandir, podemos suponer sin pérdida de generalidad que y son en sí mismos conjuntos puros. Entonces se dice que un estado está entrelazado si no es separable.${\displaystyle \rho _{i}^{A}}$${\displaystyle \rho _{i}^{B}}$${\displaystyle \rho _{i}^{A}}$${\displaystyle \rho _{i}^{B}}$

En general, se considera difícil determinar si un estado mixto está entrelazado o no. Se ha demostrado que el caso bipartito general es NP-hard . ^[65] Para los casos 2 × 2 y 2 × 3 , un criterio necesario y suficiente para la separabilidad lo proporciona la famosa condición de transposición parcial positiva (PPT) . ^[66]

La idea de una matriz de densidad reducida fue introducida por Paul Dirac en 1930. ^[67] Considérese como arriba los sistemas A y B cada uno con un espacio de Hilbert H _A , H _B . Sea el estado del sistema compuesto

${\displaystyle |\Psi \rangle \in H_{A}\otimes H_{B}.}$

Como se indicó anteriormente, en general no hay forma de asociar un estado puro al sistema componente A. Sin embargo, aún es posible asociar una matriz de densidad. Sea

${\displaystyle \rho _{T}=|\Psi \rangle \;\langle \Psi |}$.

que es el operador de proyección sobre este estado. El estado de A es la traza parcial de ρ _T sobre la base del sistema B :

${\displaystyle \rho _{A}\ {\stackrel {\mathrm {def} }{=}}\ \sum _{j}^{N_{B}}\left(I_{A}\otimes \langle j|_{B}\right)\left(|\Psi \rangle \langle \Psi |\right)\left(I_{A}\otimes |j\rangle _{B}\right)={\hbox{Tr}}_{B}\;\rho _{T}.}$

La suma se produce sobre y el operador identidad en . ρ _A a veces se denomina matriz de densidad reducida de ρ en el subsistema A . Coloquialmente, "trazamos" el sistema B para obtener la matriz de densidad reducida en A .${\displaystyle N_{B}:=\dim(H_{B})}$${\displaystyle I_{A}}$${\displaystyle H_{A}}$

Por ejemplo, la matriz de densidad reducida de A para el estado entrelazado

${\displaystyle {\tfrac {1}{\sqrt {2}}}\left(|0\rangle _{A}\otimes |1\rangle _{B}-|1\rangle _{A}\otimes |0\rangle _{B}\right),}$

Lo discutido anteriormente es

${\displaystyle \rho _{A}={\tfrac {1}{2}}\left(|0\rangle _{A}\langle 0|_{A}+|1\rangle _{A}\langle 1|_{A}\right).}$

Esto demuestra que, como se esperaba, la matriz de densidad reducida para un conjunto puro entrelazado es un conjunto mixto. Tampoco es sorprendente que la matriz de densidad de A para el estado de producto puro discutido anteriormente sea${\displaystyle |\psi \rangle _{A}\otimes |\phi \rangle _{B}}$

${\displaystyle \rho _{A}=|\psi \rangle _{A}\langle \psi |_{A}}$.

En general, un estado puro bipartito ρ está enredado si y solo si sus estados reducidos son mixtos en lugar de puros.

Las matrices de densidad reducida se calcularon explícitamente en diferentes cadenas de espín con un estado fundamental único. Un ejemplo es la cadena de espín unidimensional AKLT : ^[68] el estado fundamental se puede dividir en un bloque y un entorno. La matriz de densidad reducida del bloque es proporcional a un proyector a un estado fundamental degenerado de otro hamiltoniano.

La matriz de densidad reducida también se evaluó para cadenas de espines XY , donde tiene rango completo. Se demostró que en el límite termodinámico, el espectro de la matriz de densidad reducida de un gran bloque de espines es una secuencia geométrica exacta ^[69] en este caso.

En la teoría de la información cuántica, los estados entrelazados se consideran un 'recurso', es decir, algo costoso de producir y que permite implementar transformaciones valiosas. ^{[70] [71]} El escenario en el que esta perspectiva es más evidente es el de los "laboratorios distantes", es decir, dos sistemas cuánticos etiquetados como "A" y "B" sobre cada uno de los cuales se pueden realizar operaciones cuánticas arbitrarias , pero que no interactúan entre sí cuánticamente. La única interacción permitida es el intercambio de información clásica, que combinado con las operaciones cuánticas locales más generales da lugar a la clase de operaciones llamadas LOCC (operaciones locales y comunicación clásica). Estas operaciones no permiten la producción de estados entrelazados entre los sistemas A y B. Pero si a A y B se les proporciona un suministro de estados entrelazados, entonces estos, junto con las operaciones LOCC pueden permitir una clase más grande de transformaciones. Por ejemplo, una interacción entre un qubit de A y un qubit de B se puede realizar teletransportando primero el qubit de A a B, luego dejándolo interactuar con el qubit de B (que ahora es una operación LOCC, ya que ambos qubits están en el laboratorio de B) y luego teletransportando el qubit de regreso a A. Dos estados entrelazados al máximo de dos qubits se utilizan en este proceso. Por lo tanto, los estados entrelazados son un recurso que permite la realización de interacciones cuánticas (o de canales cuánticos) en un entorno donde solo están disponibles los LOCC, pero se consumen en el proceso. Hay otras aplicaciones en las que el entrelazamiento puede verse como un recurso, por ejemplo, la comunicación privada o la distinción de estados cuánticos. ^[72]

No todos los estados cuánticos tienen el mismo valor como recurso. Para cuantificar este valor, se pueden utilizar diferentes medidas de entrelazamiento (ver más abajo), que asignan un valor numérico a cada estado cuántico. Sin embargo, a menudo es interesante conformarse con una forma más burda de comparar los estados cuánticos. Esto da lugar a diferentes esquemas de clasificación. La mayoría de las clases de entrelazamiento se definen en función de si los estados se pueden convertir a otros estados utilizando LOCC o una subclase de estas operaciones. Cuanto menor sea el conjunto de operaciones permitidas, más precisa será la clasificación. Algunos ejemplos importantes son:

• Si dos estados pueden transformarse entre sí mediante una operación unitaria local, se dice que están en la misma clase LU . Esta es la mejor de las clases consideradas habitualmente. Dos estados en la misma clase LU tienen el mismo valor para las medidas de entrelazamiento y el mismo valor como recurso en el entorno de laboratorios distantes. Hay un número infinito de clases LU diferentes (incluso en el caso más simple de dos cúbits en un estado puro). ^{[73] [74]}
• Si dos estados pueden transformarse entre sí mediante operaciones locales que incluyen mediciones con probabilidad mayor que 0, se dice que están en la misma 'clase SLOCC' ("LOCC estocástico"). Cualitativamente, dos estados y en la misma clase SLOCC son igualmente poderosos (ya que puedo transformar uno en el otro y luego hacer lo que me permita hacer), pero dado que las transformaciones y pueden tener éxito con diferente probabilidad, ya no son igualmente valiosas. Por ejemplo, para dos qubits puros solo hay dos clases SLOCC: los estados entrelazados (que contienen tanto los estados de Bell (máximamente entrelazados) como los estados débilmente entrelazados como ) y los separables (es decir, estados producto como ). ^{[75] [76]}${\displaystyle \rho _{1}}$${\displaystyle \rho _{2}}$${\displaystyle \rho _{1}\to \rho _{2}}$${\displaystyle \rho _{2}\to \rho _{1}}$${\displaystyle |00\rangle +0.01|11\rangle }$${\displaystyle |00\rangle }$
• En lugar de considerar transformaciones de copias individuales de un estado (como ), se pueden definir clases basadas en la posibilidad de transformaciones de múltiples copias. Por ejemplo, hay ejemplos en los que es imposible por LOCC, pero es posible. Una clasificación muy importante (y muy burda) se basa en la propiedad de si es posible transformar un número arbitrario de copias de un estado en al menos un estado entrelazado puro. Los estados que tienen esta propiedad se denominan destilables. Estos estados son los estados cuánticos más útiles ya que, dada la cantidad suficiente de ellos, se pueden transformar (con operaciones locales) en cualquier estado entrelazado y, por lo tanto, permiten todos los usos posibles. Inicialmente, fue una sorpresa que no todos los estados entrelazados sean destilables, los que no lo son se denominan " enredados ligados ". ^{[77] [72]}${\displaystyle \rho _{1}\to \rho _{2}}$${\displaystyle \rho _{1}\to \rho _{2}}$${\displaystyle \rho _{1}\otimes \rho _{1}\to \rho _{2}}$${\displaystyle \rho }$

Una clasificación diferente del entrelazamiento se basa en lo que las correlaciones cuánticas presentes en un estado permiten que A y B hagan: se distinguen tres subconjuntos de estados entrelazados: (1) los estados no locales , que producen correlaciones que no pueden explicarse mediante un modelo de variable oculta local y, por lo tanto, violan una desigualdad de Bell, (2) los estados controlables que contienen correlaciones suficientes para que A modifique ("controle") mediante mediciones locales el estado reducido condicional de B de tal manera que A pueda demostrar a B que el estado que poseen está efectivamente entrelazado, y finalmente (3) aquellos estados entrelazados que no son ni no locales ni controlables. Los tres conjuntos no están vacíos. ^[78]

En esta sección, se analiza la entropía de un estado mixto y cómo puede verse como una medida del entrelazamiento cuántico.

En la teoría clásica de la información, H , la entropía de Shannon , está asociada a una distribución de probabilidad, , de la siguiente manera: ^[79]${\displaystyle p_{1},\cdots ,p_{n}}$

${\displaystyle H(p_{1},\cdots ,p_{n})=-\sum _{i}p_{i}\log _{2}p_{i}.}$

Dado que un estado mixto ρ es una distribución de probabilidad sobre un conjunto, esto conduce naturalmente a la definición de la entropía de von Neumann :

${\displaystyle S(\rho )=-{\hbox{Tr}}\left(\rho \log _{2}{\rho }\right).}$

En general, se utiliza el cálculo funcional de Borel para calcular una función no polinómica como log ₂ ( ρ ) . Si el operador no negativo ρ actúa sobre un espacio de Hilbert de dimensión finita y tiene valores propios , log ₂ ( ρ ) resulta ser nada más que el operador con los mismos vectores propios, pero los valores propios . La entropía de Shannon es entonces:${\displaystyle \lambda _{1},\cdots ,\lambda _{n}}$${\displaystyle \log _{2}(\lambda _{1}),\cdots ,\log _{2}(\lambda _{n})}$

${\displaystyle S(\rho )=-{\hbox{Tr}}\left(\rho \log _{2}{\rho }\right)=-\sum _{i}\lambda _{i}\log _{2}\lambda _{i}}$.

Dado que un evento de probabilidad 0 no debería contribuir a la entropía, y dado que

${\displaystyle \lim _{p\to 0}p\log p=0,}$

Se adopta la convención 0 log(0) = 0. Esto se extiende también al caso de dimensión infinita: si ρ tiene resolución espectral

${\displaystyle \rho =\int \lambda dP_{\lambda },}$

asumir la misma convención al calcular

${\displaystyle \rho \log _{2}\rho =\int \lambda \log _{2}\lambda dP_{\lambda }.}$

Al igual que en la mecánica estadística , cuanto mayor sea la incertidumbre (número de microestados) que posea el sistema, mayor será la entropía. Por ejemplo, la entropía de cualquier estado puro es cero, lo que no sorprende, ya que no hay incertidumbre sobre un sistema en estado puro. La entropía de cualquiera de los dos subsistemas del estado entrelazado analizados anteriormente es log(2) (que puede demostrarse que es la entropía máxima para estados mixtos 2 × 2 ).

La entropía proporciona una herramienta que puede utilizarse para cuantificar el entrelazamiento, aunque existen otras medidas de entrelazamiento. ^{[80] [81]} Si el sistema general es puro, la entropía de un subsistema puede utilizarse para medir su grado de entrelazamiento con los demás subsistemas. Para los estados puros bipartitos, la entropía de von Neumann de los estados reducidos es la única medida de entrelazamiento en el sentido de que es la única función en la familia de estados que satisface ciertos axiomas requeridos para una medida de entrelazamiento. ^[82]

Es un resultado clásico que la entropía de Shannon alcanza su máximo en, y solo en, la distribución de probabilidad uniforme {1/ n ,...,1/ n }. Por lo tanto, se dice que un estado puro bipartito ρ ∈ H _A ⊗ H _B es un estado máximamente entrelazado si el estado reducido de cada subsistema de ρ es la matriz diagonal

${\displaystyle {\begin{bmatrix}{\frac {1}{n}}&&\\&\ddots &\\&&{\frac {1}{n}}\end{bmatrix}}.}$

Para estados mixtos, la entropía de von Neumann reducida no es la única medida de entrelazamiento razonable.

Por otra parte, la definición de teoría de la información está estrechamente relacionada con la entropía en el sentido de la mecánica estadística ^[83] (al comparar las dos definiciones en el presente contexto, se acostumbra establecer la constante de Boltzmann k = 1 ). Por ejemplo, por propiedades del cálculo funcional de Borel , vemos que para cualquier operador unitario U ,

${\displaystyle S(\rho )=S\left(U\rho U^{*}\right).}$

De hecho, sin esta propiedad, la entropía de von Neumann no estaría bien definida.

En particular, U podría ser el operador de evolución temporal del sistema, es decir,

${\displaystyle U(t)=\exp \left({\frac {-iHt}{\hbar }}\right),}$

donde H es el hamiltoniano del sistema. Aquí la entropía no varía.

La entropía de Rényi también se puede utilizar como medida de entrelazamiento. ^[84]

Las medidas de entrelazamiento cuantifican la cantidad de entrelazamiento en un estado cuántico (a menudo visto como bipartito). Como se mencionó anteriormente, la entropía de entrelazamiento es la medida estándar de entrelazamiento para estados puros (pero ya no es una medida de entrelazamiento para estados mixtos). Para los estados mixtos, existen algunas medidas de entrelazamiento en la literatura ^[80] y ninguna es estándar.

• Costo de enredo
• Enredo destilable
• Enredo de formación
• Concurrencia
• Entropía relativa del entrelazamiento
• Enredo aplastado
• Negatividad logarítmica

La mayoría (pero no todas) de estas medidas de entrelazamiento se reducen para estados puros a entropía de entrelazamiento, y son difíciles ( NP-duras ) de calcular para estados mixtos a medida que la dimensión del sistema entrelazado crece. ^[85]

El teorema de Reeh-Schlieder de la teoría cuántica de campos se considera a veces como un análogo del entrelazamiento cuántico.

El entrelazamiento tiene muchas aplicaciones en la teoría de la información cuántica . Con su ayuda se pueden lograr tareas que de otro modo serían imposibles.

Entre las aplicaciones más conocidas del entrelazamiento se encuentran la codificación superdensa y la teletransportación cuántica. ^[86]

La mayoría de los investigadores creen que el entrelazamiento es necesario para lograr la computación cuántica (aunque algunos lo discuten). ^[87]

El entrelazamiento se utiliza en algunos protocolos de criptografía cuántica , ^{[88] [89]} pero para demostrar la seguridad de la distribución de clave cuántica (QKD) bajo supuestos estándar no se requiere entrelazamiento. ^[90] Sin embargo, la seguridad independiente del dispositivo de QKD se muestra explotando el entrelazamiento entre los socios de comunicación. ^[91]

Hay varios estados entrelazados canónicos que aparecen a menudo en la teoría y en los experimentos.

Para dos qubits , los estados de Bell son

${\displaystyle |\Phi ^{\pm }\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |0\rangle _{B}\pm |1\rangle _{A}\otimes |1\rangle _{B})}$

${\displaystyle |\Psi ^{\pm }\rangle ={\frac {1}{\sqrt {2}}}(|0\rangle _{A}\otimes |1\rangle _{B}\pm |1\rangle _{A}\otimes |0\rangle _{B}).}$

Estos cuatro estados puros están entrelazados al máximo (según la entropía de entrelazamiento ) y forman una base ortonormal (álgebra lineal) del espacio de Hilbert de los dos cúbits. Desempeñan un papel fundamental en el teorema de Bell .

Para M>2 qubits, el estado GHZ es

${\displaystyle |\mathrm {GHZ} \rangle ={\frac {|0\rangle ^{\otimes M}+|1\rangle ^{\otimes M}}{\sqrt {2}}},}$

que se reduce al estado de Bell para . El estado GHZ tradicional se definió para . Los estados GHz se extienden ocasionalmente a qudits , es decir, sistemas de d en lugar de 2 dimensiones.${\displaystyle |\Phi ^{+}\rangle }$${\displaystyle M=2}$${\displaystyle M=3}$

También para M>2 qubits, existen estados de espín comprimido , una clase de estados coherentes comprimidos que satisfacen ciertas restricciones sobre la incertidumbre de las mediciones de espín, que están necesariamente entrelazados. ^[92] Los estados de espín comprimido son buenos candidatos para mejorar las mediciones de precisión utilizando entrelazamiento cuántico. ^[93]

Para dos modos bosónicos , un estado NOON es

${\displaystyle |\psi _{\text{NOON}}\rangle ={\frac {|N\rangle _{a}|0\rangle _{b}+|{0}\rangle _{a}|{N}\rangle _{b}}{\sqrt {2}}},\,}$

Esto es como el estado de Bell, excepto que los kets base 0 y 1 han sido reemplazados por "los N fotones están en un modo" y "los N fotones están en el otro modo".${\displaystyle |\Psi ^{+}\rangle }$

Por último, también existen estados Fock gemelos para modos bosónicos, que pueden crearse alimentando un estado Fock a dos brazos que conducen a un divisor de haz. Son la suma de múltiplos de estados NOON y pueden utilizarse para alcanzar el límite de Heisenberg. ^[94]

En el caso de las medidas de entrelazamiento elegidas adecuadamente, los estados Bell, GHZ y NOON están entrelazados al máximo, mientras que los estados de espín comprimido y los estados gemelos de Fock están entrelazados solo parcialmente. Los estados parcialmente entrelazados son, en general, más fáciles de preparar experimentalmente.

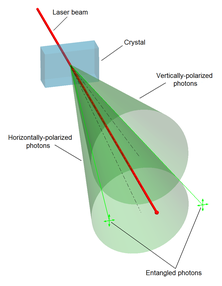
El entrelazamiento se crea generalmente por interacciones directas entre partículas subatómicas. Estas interacciones pueden tomar numerosas formas. Uno de los métodos más comúnmente utilizados es la conversión descendente paramétrica espontánea para generar un par de fotones entrelazados en polarización. ^{[72] [95]} Otros métodos incluyen el uso de un acoplador de fibra para confinar y mezclar fotones, fotones emitidos por la cascada de desintegración del biexcitón en un punto cuántico , ^[96] el uso del efecto Hong-Ou-Mandel , etc. El entrelazamiento cuántico de una partícula y su antipartícula , como un electrón y un positrón , se puede crear por superposición parcial de las funciones de onda cuánticas correspondientes en el interferómetro de Hardy . ^{[97] [98]} En las primeras pruebas del teorema de Bell, las partículas entrelazadas se generaron utilizando cascadas atómicas . ^[24]

También es posible crear entrelazamientos entre sistemas cuánticos que nunca interactuaron directamente, mediante el uso del intercambio de entrelazamientos . Dos partículas idénticas preparadas independientemente también pueden estar entrelazadas si sus funciones de onda simplemente se superponen espacialmente, al menos parcialmente. ^[99]

Una matriz de densidad ρ se denomina separable si se puede escribir como una suma convexa de estados producto, es decir, con probabilidades. Por definición, un estado está entrelazado si no es separable.$${\displaystyle {\rho =\sum _{j}p_{j}\rho _{j}^{(A)}\otimes \rho _{j}^{(B)}}}$$${\displaystyle 0\leq p_{j}\leq 1}$

Para los sistemas 2-Qubit y Qubit-Qutrit (2 × 2 y 2 × 3 respectivamente) el criterio simple de Peres-Horodecki proporciona un criterio necesario y suficiente para la separabilidad y, por lo tanto, inadvertidamente, para detectar el entrelazamiento. Sin embargo, para el caso general, el criterio es simplemente necesario para la separabilidad, ya que el problema se vuelve NP-hard cuando se generaliza. ^{[100] [101]} Otros criterios de separabilidad incluyen (pero no se limitan a) el criterio de rango , el criterio de reducción y aquellos basados ​​en relaciones de incertidumbre. ^{[102] [103] [104] [105]} Consulte la Ref. ^[106] para una revisión de los criterios de separabilidad en sistemas de variables discretas y la Ref. ^[107] para una revisión de las técnicas y los desafíos en la certificación experimental de entrelazamiento en sistemas de variables discretas.

Jon Magne Leinaas , Jan Myrheim y Eirik Ovrum sugieren un enfoque numérico para el problema en su artículo "Aspectos geométricos del entrelazamiento". ^{[108] Leinaas et al. ofrecen un enfoque numérico, refinando iterativamente un estado separable estimado hacia el estado objetivo que se va a probar y verificando si el estado objetivo puede alcanzarse de hecho. Una implementación del algoritmo (que incluye una prueba} de criterio de Peres-Horodecki incorporada ) es la aplicación web "StateSeparator".

En sistemas de variables continuas, también se aplica el criterio de Peres-Horodecki. En concreto, Simon ^[109] formuló una versión particular del criterio de Peres-Horodecki en términos de los momentos de segundo orden de los operadores canónicos y demostró que es necesario y suficiente para los estados gaussianos de modo - (véase la referencia ^[110] para un enfoque aparentemente diferente pero esencialmente equivalente). Más tarde se descubrió ^[111] que la condición de Simon también es necesaria y suficiente para los estados gaussianos de modo -, pero ya no es suficiente para los estados gaussianos de modo -. La condición de Simon se puede generalizar teniendo en cuenta los momentos de orden superior de los operadores canónicos ^{[112] [113]} o utilizando medidas entrópicas. ^{[114] [115]}${\displaystyle 1\oplus 1}$${\displaystyle 1\oplus n}$${\displaystyle 2\oplus 2}$

El 16 de agosto de 2016, desde el Centro de Lanzamiento de Satélites de Jiuquan (China) se lanzó el primer satélite de comunicaciones cuánticas del mundo : la misión de Experimentos Cuánticos a Escala Espacial (QUESS), apodada " Micius " en honor al antiguo filósofo chino. El satélite tenía como objetivo demostrar la viabilidad de la comunicación cuántica entre la Tierra y el espacio y probar el entrelazamiento cuántico a distancias sin precedentes. ^[116]

En la edición del 16 de junio de 2017 de Science , Yin et al. informan que establecieron un nuevo récord de distancia de entrelazamiento cuántico de 1203 km, lo que demuestra la supervivencia de un par de dos fotones y una violación de una desigualdad de Bell, alcanzando una valoración CHSH de 2,37 ± 0,09, bajo estrictas condiciones de localidad de Einstein, desde el satélite Micius a bases en Lijian, Yunnan y Delingha, Quinhai, aumentando la eficiencia de transmisión sobre experimentos de fibra óptica anteriores en un orden de magnitud. ^{[117] [118]}

Las capas electrónicas de los átomos multielectrónicos siempre están formadas por electrones entrelazados. La energía de ionización correcta solo se puede calcular teniendo en cuenta el entrelazamiento de electrones. ^[119]

En 2023, el LHC, utilizando técnicas de tomografía cuántica, midió el entrelazamiento a la energía más alta hasta el momento, ^{[120] [121] [122]} una rara intersección entre la información cuántica y la física de alta energía basada en el trabajo teórico propuesto por primera vez en 2021. ^[123] El experimento fue llevado a cabo por el detector ATLAS midiendo el espín de la producción del par de quarks top y el efecto se observó con más de 5 σ de nivel de significancia, el quark top es la partícula más pesada conocida y por lo tanto tiene una vida útil muy corta ( ) siendo el único quark que se desintegra antes de sufrir hadronización ( ) y decorrelación de espín ( ), por lo que la información de espín se transfiere sin mucha pérdida a los productos de desintegración leptónica que serán capturados por el detector. ^[124] La polarización y correlación de espín de las partículas se midió y probó para el entrelazamiento con concurrencia , así como el criterio de Peres-Horodecki y posteriormente el efecto también se confirmó en el detector CMS . ^{[125] [126]}${\displaystyle \tau \sim 10^{-25}s}$${\displaystyle \sim 10^{-23}s}$${\displaystyle \sim 10^{-21}s}$

En 2020, los investigadores informaron sobre el entrelazamiento cuántico entre el movimiento de un oscilador mecánico de tamaño milimétrico y un sistema de espín distante y dispar de una nube de átomos. ^{[127] [128]} Trabajos posteriores complementaron este trabajo al entrelazar cuánticamente dos osciladores mecánicos. ^{[129] [130] [131]}

En octubre de 2018, los físicos informaron haber producido un entrelazamiento cuántico utilizando organismos vivos , particularmente entre moléculas fotosintéticas dentro de bacterias vivas y luz cuantificada . ^{[132] [133]}

Se han estudiado organismos vivos (bacterias verdes del azufre) como mediadores para crear un entrelazamiento cuántico entre modos de luz que de otro modo no interactuarían, mostrando un alto entrelazamiento entre la luz y los modos bacterianos y, hasta cierto punto, incluso un entrelazamiento dentro de las bacterias. ^[134]