No localidad cuántica

Parte de una serie de artículos sobre
Mecánica cuántica
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Ecuación de Schrödinger
Introducción Glosario Historia
Fondo Mecánica clásica Antigua teoría cuántica Notación de corchetes Hamiltoniano Interferencia
Fundamentos Complementariedad Decoherencia Enredo Nivel de energía Medición No localidad Número cuántico Estado Superposición Simetría Túnel Incertidumbre Función de onda Colapsar
Experimentos Desigualdad de Bell Desigualdad de CHSH Davisson–Germer Double-slit Elitzur–Vaidman Franck–Hertz Leggett inequality Leggett–Garg inequality Mach–Zehnder Popper Quantum eraser Delayed-choice Schrödinger's cat Stern–Gerlach Wheeler's delayed-choice
Formulations Overview Heisenberg Interaction Matrix Phase-space Schrödinger Sum-over-histories (path integral)
Equations Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Superdeterminism Many-worlds Objective-collapse Quantum logic Relational Transactional Von Neumann–Wigner
Advanced topics Relativistic quantum mechanics Quantum field theory Quantum information science Quantum computing Quantum chaos EPR paradox Density matrix Scattering theory Quantum statistical mechanics Quantum machine learning
Scientists Aharonov Bell Bethe Blackett Bloch Bohm Bohr Born Bose de Broglie Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Lamb Landau Laue Moseley Millikan Onnes Pauli Planck Rabi Raman Rydberg Schrödinger Simmons Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

En física teórica , la no localidad cuántica se refiere al fenómeno por el cual las estadísticas de medición de un sistema cuántico multipartito no permiten una interpretación con realismo local . La no localidad cuántica se ha verificado experimentalmente bajo una variedad de supuestos físicos. ^{[1] [2] [3] [4] [5]}

La no localidad cuántica no permite una comunicación más rápida que la luz [ ^6] y, por lo tanto, es compatible con la relatividad especial y su límite de velocidad universal de los objetos. Por lo tanto, la teoría cuántica es local en el sentido estricto definido por la relatividad especial y, como tal, el término "no localidad cuántica" a veces se considera un nombre inapropiado. ^[7] Aun así, da lugar a muchas de las discusiones fundamentales sobre la teoría cuántica. ^[7]

En el artículo EPR de 1935 , ^[8] Albert Einstein , Boris Podolsky y Nathan Rosen describieron "dos partículas separadas espacialmente que tienen posiciones y momentos perfectamente correlacionados" ^[9] como una consecuencia directa de la teoría cuántica. Pretendían utilizar el principio clásico de localidad para desafiar la idea de que la función de onda cuántica era una descripción completa de la realidad, pero en cambio provocaron un debate sobre la naturaleza de la realidad. ^[10] Posteriormente, Einstein presentó una variante de estas ideas en una carta a Erwin Schrödinger , ^[11] que es la versión que se presenta aquí. El estado y la notación utilizados aquí son más modernos y similares a la interpretación de David Bohm sobre EPR. ^[12] El estado cuántico de las dos partículas antes de la medición se puede escribir como donde . ^[13]$${\displaystyle \left|\psi _{AB}\right\rangle ={\frac {1}{\sqrt {2}}}\left(\left|0\right\rangle _{A}\left|1\right\rangle _{B}-\left|1\right\rangle _{A}\left|0\right\rangle _{B}\right)={\frac {1}{\sqrt {2}}}\left(\left|-\right\rangle _{A}\left|+\right\rangle _{B}-\left|+\right\rangle _{A}\left|-\right\rangle _{B}\right)}$$${\textstyle \left|\pm \right\rangle ={\frac {1}{\sqrt {2}}}\left(\left|0\right\rangle \pm \left|1\right\rangle \right)}$

Aquí, los subíndices "A" y "B" distinguen las dos partículas, aunque es más conveniente y habitual referirse a estas partículas como en posesión de dos experimentalistas llamados Alice y Bob . Las reglas de la teoría cuántica dan predicciones para los resultados de las mediciones realizadas por los experimentalistas. Alice, por ejemplo, medirá que su partícula tiene espín hacia arriba en un promedio del cincuenta por ciento de las mediciones. Sin embargo, según la interpretación de Copenhague, la medición de Alice hace que el estado de las dos partículas colapse , de modo que si Alice realiza una medición de espín en la dirección z, es decir, con respecto a la base , entonces el sistema de Bob quedará en uno de los estados . Del mismo modo, si Alice realiza una medición de espín en la dirección x, es decir, con respecto a la base , entonces el sistema de Bob quedará en uno de los estados . Schrödinger se refirió a este fenómeno como " dirección ". ^[14] Esta dirección ocurre de tal manera que no se puede enviar ninguna señal al realizar dicha actualización de estado; La no localidad cuántica no se puede utilizar para enviar mensajes instantáneamente y, por lo tanto, no está en conflicto directo con las preocupaciones de causalidad en la relatividad especial . ^[13]${\displaystyle \{\left|0\right\rangle _{A},\left|1\right\rangle _{A}\}}$${\displaystyle \{\left|0\right\rangle _{B},\left|1\right\rangle _{B}\}}$${\displaystyle \{\left|+\right\rangle _{A},\left|-\right\rangle _{A}\}}$${\displaystyle \{\left|+\right\rangle _{B},\left|-\right\rangle _{B}\}}$

En la perspectiva de Copenhague de este experimento, la medición de Alice (y en particular su elección de medición) tiene un efecto directo en el estado de Bob. Sin embargo, bajo el supuesto de localidad, las acciones sobre el sistema de Alice no afectan el estado "verdadero" u "óntico" del sistema de Bob. Vemos que el estado óntico del sistema de Bob debe ser compatible con uno de los estados cuánticos o , ya que Alice puede hacer una medición que concluya con uno de esos estados siendo la descripción cuántica de su sistema. Al mismo tiempo, también debe ser compatible con uno de los estados cuánticos o por la misma razón. Por lo tanto, el estado óntico del sistema de Bob debe ser compatible con al menos dos estados cuánticos; el estado cuántico no es, por lo tanto, un descriptor completo de su sistema. Einstein, Podolsky y Rosen vieron esto como evidencia de lo incompleto de la interpretación de Copenhague de la teoría cuántica, ya que la función de onda explícitamente no es una descripción completa de un sistema cuántico bajo este supuesto de localidad. Su artículo concluye: ^[8]${\displaystyle \left|\uparrow \right\rangle _{B}}$${\displaystyle \left|\downarrow \right\rangle _{B}}$${\displaystyle \left|\leftarrow \right\rangle _{B}}$${\displaystyle \left|\rightarrow \right\rangle _{B}}$

Si bien hemos demostrado que la función de onda no proporciona una descripción completa de la realidad física, dejamos abierta la cuestión de si tal descripción existe o no. Creemos, sin embargo, que tal teoría es posible.

Aunque varios autores (entre los que destacaba Niels Bohr ) criticaron la terminología ambigua del artículo de EPR, ^{[15] [16]} el experimento mental generó, no obstante, un gran interés. Su noción de una "descripción completa" se formalizó posteriormente mediante la sugerencia de variables ocultas que determinan las estadísticas de los resultados de las mediciones, pero a las que un observador no tiene acceso. ^[17] La ​​mecánica de Bohm proporciona una forma de completar la mecánica cuántica, con la introducción de variables ocultas; sin embargo, la teoría es explícitamente no local. ^[18] Por lo tanto, la interpretación no da una respuesta a la pregunta de Einstein, que era si se podía dar o no una descripción completa de la mecánica cuántica en términos de variables ocultas locales de acuerdo con el "Principio de acción local". ^[19]

En 1964, John Bell respondió a la pregunta de Einstein demostrando que dichas variables ocultas locales nunca pueden reproducir la gama completa de resultados estadísticos predichos por la teoría cuántica. ^[20] Bell demostró que una hipótesis de variable oculta local conduce a restricciones en la fuerza de las correlaciones de los resultados de las mediciones. Si las desigualdades de Bell se violan experimentalmente como predice la mecánica cuántica, entonces la realidad no puede ser descrita por variables ocultas locales y el misterio de la causalidad cuántica no local permanece. Sin embargo, Bell señala que el modelo de variable oculta no local de Bohm es diferente: ^[20]

Esta [estructura groseramente no local] es característica... de cualquier teoría que reproduzca exactamente las predicciones de la mecánica cuántica.

Clauser , Horne, Shimony y Holt (CHSH) reformularon estas desigualdades de una manera que fuera más propicia para la prueba experimental (véase desigualdad CHSH ). ^[21]

En el escenario propuesto por Bell (un escenario de Bell), dos experimentadores, Alice y Bob, realizan experimentos en laboratorios separados. En cada ejecución, Alice (Bob) realiza un experimento en su (su) laboratorio, obteniendo el resultado . Si Alice y Bob repiten sus experimentos varias veces, entonces pueden estimar las probabilidades , es decir, la probabilidad de que Alice y Bob observen respectivamente los resultados cuando realizan respectivamente los experimentos x, y. En lo sucesivo, cada uno de esos conjuntos de probabilidades se denotará simplemente por . En la jerga de la no localidad cuántica, se denomina caja. ^[22]${\displaystyle x}$ ${\displaystyle (y)}$${\displaystyle a}$ ${\displaystyle (b)}$${\displaystyle P(a,b|x,y)}$${\displaystyle a,b}$${\displaystyle \{P(a,b|x,y):a,b,x,y\}}$${\displaystyle P(a,b|x,y)}$${\displaystyle P(a,b|x,y)}$

Bell formalizó la idea de una variable oculta al introducir el parámetro para caracterizar localmente los resultados de las mediciones en cada sistema: ^[20] "Es indiferente... si λ denota una sola variable o un conjunto... y si las variables son discretas o continuas". Sin embargo, es equivalente (y más intuitivo) pensar en ella como una "estrategia" o "mensaje" local que ocurre con cierta probabilidad cuando Alice y Bob reinician su configuración experimental. La suposición de causalidad local de Bell estipula entonces que cada estrategia local define las distribuciones de resultados independientes si Alice lleva a cabo el experimento x y Bob lleva a cabo el experimento :${\displaystyle \lambda }$${\displaystyle \lambda }$${\displaystyle \rho (\lambda )}$${\displaystyle y}$

$${\displaystyle P(a,b|x,y,\lambda _{A},\lambda _{B})=P_{A}(a|x,\lambda _{A})P_{B}(b|y,\lambda _{B})}$$

Aquí ( ) denota la probabilidad de que Alice (Bob) obtenga el resultado cuando realiza el experimento y la variable local que describe su experimento tiene valor ( ).${\displaystyle P_{A}(a|x,\lambda _{A})}$${\displaystyle P_{B}(b|y,\lambda _{B})}$${\displaystyle a}$ ${\displaystyle (b)}$${\displaystyle x}$ ${\displaystyle (y)}$${\displaystyle \lambda _{A}}$${\displaystyle \lambda _{B}}$

Supongamos que se pueden tomar valores de un conjunto determinado . Si cada par de valores tiene una probabilidad asociada de ser seleccionado (se permite la aleatoriedad compartida, es decir, se pueden correlacionar), entonces se puede promediar esta distribución para obtener una fórmula para la probabilidad conjunta de cada resultado de medición:${\displaystyle \lambda _{A},\lambda _{B}}$${\displaystyle \Lambda }$${\displaystyle \lambda _{A},\lambda _{B}\in \Lambda }$${\displaystyle \rho (\lambda _{A},\lambda _{B})}$${\displaystyle \lambda _{A},\lambda _{B}}$

$${\displaystyle P(a,b|x,y)=\sum _{\lambda _{A},\lambda _{B}\in \Lambda }\rho (\lambda _{A},\lambda _{B})P_{A}(a|x,\lambda _{A})P_{B}(b|y,\lambda _{B})}$$

Una caja que admite tal descomposición se denomina caja local de Bell o caja clásica. Fijando el número de valores posibles que puede tomar cada una, se puede representar cada caja como un vector finito con entradas . En esa representación, el conjunto de todas las cajas clásicas forma un politopo convexo . En el escenario de Bell estudiado por CHSH, donde puede tomar valores dentro de , cualquier caja local de Bell debe satisfacer la desigualdad de CHSH:${\displaystyle a,b,x,y}$${\displaystyle P(a,b|x,y)}$${\displaystyle \left(P(a,b|x,y)\right)_{a,b,x,y}}$${\displaystyle a,b,x,y}$${\displaystyle {0,1}}$${\displaystyle P(a,b|x,y)}$

$${\displaystyle S_{\rm {CHSH}}\equiv E(0,0)+E(1,0)+E(0,1)-E(1,1)\leq 2,}$$

dónde$${\displaystyle E(x,y)\equiv \sum _{a,b=0,1}(-1)^{a+b}P(a,b|x,y).}$$

Las consideraciones anteriores se aplican para modelar un experimento cuántico. Consideremos dos partes que realizan mediciones de polarización local en un estado fotónico bipartito. El resultado de la medición para la polarización de un fotón puede tomar uno de dos valores (informalmente, si el fotón está polarizado en esa dirección o en la dirección ortogonal). Si a cada parte se le permite elegir entre solo dos direcciones de polarización diferentes, el experimento encaja dentro del escenario CHSH. Como señaló CHSH, existe un estado cuántico y direcciones de polarización que generan una caja con igual a . Esto demuestra una forma explícita en la que una teoría con estados ontológicos que son locales, con mediciones locales y solo acciones locales no puede coincidir con las predicciones probabilísticas de la teoría cuántica, refutando la hipótesis de Einstein. Experimentalistas como Alain Aspect han verificado la violación cuántica de la desigualdad CHSH ^[1] así como otras formulaciones de la desigualdad de Bell, para invalidar la hipótesis de las variables ocultas locales y confirmar que la realidad es de hecho no local en el sentido EPR.${\displaystyle P(a,b|x,y)}$${\displaystyle S_{\rm {CHSH}}}$${\displaystyle 2{\sqrt {2}}\approx 2.828}$

La demostración de Bell es probabilística en el sentido de que muestra que las probabilidades precisas predichas por la mecánica cuántica para algunos escenarios entrelazados no pueden cumplirse mediante una teoría de variables ocultas locales. (Para abreviar, aquí y en adelante "teoría local" significa "teoría de variables ocultas locales"). Sin embargo, la mecánica cuántica permite una violación aún más fuerte de las teorías locales: una posibilista, en la que las teorías locales ni siquiera pueden estar de acuerdo con la mecánica cuántica sobre qué eventos son posibles o imposibles en un escenario entrelazado. La primera prueba de este tipo se debió a Daniel Greenberger , Michael Horne y Anton Zeilinger en 1993 ^[23]. El estado involucrado a menudo se llama estado GHZ .

En 1993, Lucien Hardy demostró una prueba lógica de no localidad cuántica que, como la prueba GHZ, es una prueba posibilista. ^{[24] [25] [26]} Comienza con la observación de que el estado definido a continuación se puede escribir de algunas maneras sugerentes: donde, como arriba, .${\displaystyle \left|\psi \right\rangle }$$${\displaystyle \left|\psi \right\rangle ={\frac {1}{\sqrt {3}}}\left(\left|00\right\rangle +\left|01\right\rangle +\left|10\right\rangle \right)={\frac {1}{\sqrt {3}}}\left({\sqrt {2}}\left|+0\right\rangle +{\frac {1}{\sqrt {2}}}\left(\left|+1\right\rangle +\left|-1\right\rangle \right)\right)={\frac {1}{\sqrt {3}}}\left({\sqrt {2}}\left|0+\right\rangle +{\frac {1}{\sqrt {2}}}\left(\left|1+\right\rangle +\left|1-\right\rangle \right)\right)}$$${\displaystyle |\pm \rangle ={\tfrac {1}{\sqrt {2}}}(\left|0\right\rangle \pm \left|1\right\rangle )}$

El experimento consiste en que este estado entrelazado se comparte entre dos experimentadores, cada uno de los cuales tiene la capacidad de medir con respecto a la base o . Vemos que si cada uno mide con respecto a , entonces nunca ven el resultado . Si uno mide con respecto a y el otro , nunca ven los resultados . Sin embargo, a veces ven el resultado cuando miden con respecto a , ya que${\displaystyle \{\left|0\right\rangle ,\left|1\right\rangle \}}$${\displaystyle \{\left|+\right\rangle ,\left|-\right\rangle \}}$${\displaystyle \{\left|0\right\rangle ,\left|1\right\rangle \}}$${\displaystyle \left|11\right\rangle }$${\displaystyle \{\left|0\right\rangle ,\left|1\right\rangle \}}$${\displaystyle \{\left|+\right\rangle ,\left|-\right\rangle \}}$${\displaystyle \left|-0\right\rangle ,}$ ${\displaystyle \left|0-\right\rangle .}$${\displaystyle \left|--\right\rangle }$${\displaystyle \{\left|+\right\rangle ,\left|-\right\rangle \}}$${\displaystyle \langle --|\psi \rangle =-{\tfrac {1}{2{\sqrt {3}}}}\neq 0.}$

Esto nos lleva a la paradoja: si tenemos el resultado , concluimos que si uno de los experimentadores hubiera medido con respecto a la base, el resultado debería haber sido o , ya que y son imposibles. Pero entonces, si ambos hubieran medido con respecto a la base, por localidad el resultado debería haber sido , lo cual también es imposible.${\displaystyle |--\rangle }$${\displaystyle \{\left|0\right\rangle ,\left|1\right\rangle \}}$${\displaystyle |{-}1\rangle }$${\displaystyle |1-\rangle }$${\displaystyle |{-}0\rangle }$${\displaystyle |0-\rangle }$${\displaystyle \{\left|0\right\rangle ,\left|1\right\rangle \}}$${\displaystyle \left|11\right\rangle }$

El trabajo de Bancal et al. ^[27] generaliza el resultado de Bell al demostrar que las correlaciones alcanzables en la teoría cuántica también son incompatibles con una gran clase de modelos de variables ocultas superlumínicas. En este marco, se excluye la señalización más rápida que la luz. Sin embargo, la elección de la configuración de una de las partes puede influir en las variables ocultas en la ubicación distante de otra parte, si hay tiempo suficiente para que una influencia superlumínica (de velocidad finita, pero por lo demás desconocida) se propague de un punto al otro. En este escenario, cualquier experimento bipartito que revele la no localidad de Bell puede simplemente proporcionar límites inferiores a la velocidad de propagación de la influencia oculta. Los experimentos cuánticos con tres o más partes pueden, no obstante, refutar todos esos modelos de variables ocultas no locales. ^[27]

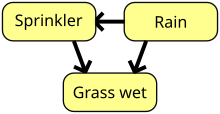
Las variables aleatorias medidas en un experimento general pueden depender entre sí de maneras complicadas. En el campo de la inferencia causal, tales dependencias se representan a través de redes bayesianas : gráficos acíclicos dirigidos donde cada nodo representa una variable y un borde de una variable a otra significa que la primera influye en la segunda y no de otra manera, vea la figura. En un experimento de Bell bipartito estándar, la configuración de Alice (Bob) ( ), junto con su variable local ( ), influyen en su resultado local ( ). El teorema de Bell puede entonces interpretarse como una separación entre las predicciones cuánticas y clásicas en un tipo de estructuras causales con solo un nodo oculto . Se han establecido separaciones similares en otros tipos de estructuras causales. ^[28] La caracterización de los límites para las correlaciones clásicas en tales escenarios de Bell extendidos es un desafío, pero existen métodos computacionales prácticos completos para lograrlo. ^{[29] [30]}${\displaystyle x}$${\displaystyle y}$${\displaystyle \lambda _{A}}$${\displaystyle \lambda _{B}}$${\displaystyle a}$${\displaystyle b}$${\displaystyle (\lambda _{A},\lambda _{B})}$

A veces se entiende que la no localidad cuántica es equivalente al entrelazamiento. Sin embargo, no es así. El entrelazamiento cuántico solo se puede definir dentro del formalismo de la mecánica cuántica, es decir, es una propiedad que depende del modelo. Por el contrario, la no localidad se refiere a la imposibilidad de una descripción de las estadísticas observadas en términos de un modelo de variable oculta local, por lo que es independiente del modelo físico utilizado para describir el experimento.

Es cierto que para cualquier estado entrelazado puro existe una selección de mediciones que producen correlaciones no locales de Bell, pero la situación es más compleja para los estados mixtos. Mientras que cualquier estado no local de Bell debe estar entrelazado, existen estados entrelazados (mixtos) que no producen correlaciones no locales de Bell ^[31] (aunque, operando sobre varias copias de algunos de esos estados, ^[32] o llevando a cabo post-selecciones locales, ^[33] es posible observar efectos no locales). Además, mientras que existen catalizadores para el entrelazamiento, ^[34] no los hay para la no localidad. ^[35] Finalmente, se han encontrado ejemplos razonablemente simples de desigualdades de Bell para las cuales el estado cuántico que da la violación más grande nunca es un estado entrelazado al máximo, lo que demuestra que el entrelazamiento, en cierto sentido, ni siquiera es proporcional a la no localidad. ^{[36] [37] [38]}

Como se muestra, las estadísticas alcanzables por dos o más partes que realizan experimentos en un sistema clásico están restringidas de una manera no trivial. Análogamente, las estadísticas alcanzables por observadores separados en una teoría cuántica también resultan estar restringidas. La primera derivación de un límite estadístico no trivial en el conjunto de correlaciones cuánticas, debido a B. Tsirelson , ^[39] se conoce como límite de Tsirelson . Considere el escenario de Bell CHSH detallado anteriormente, pero esta vez suponga que, en sus experimentos, Alice y Bob están preparando y midiendo sistemas cuánticos. En ese caso, se puede demostrar que el parámetro CHSH está acotado por

${\displaystyle -2{\sqrt {2}}\leq \mathrm {CHSH} \leq 2{\sqrt {2}}.}$

Matemáticamente, una caja admite una realización cuántica si y sólo si existen un par de espacios de Hilbert , un vector normalizado y operadores de proyección tales que${\displaystyle P(a,b|x,y)}$${\displaystyle H_{A},H_{B}}$${\displaystyle \left|\psi \right\rangle \in H_{A}\otimes H_{B}}$${\displaystyle E_{a}^{x}:H_{A}\to H_{A},F_{b}^{y}:H_{B}\to H_{B}}$

1. Para todos los , los conjuntos representan mediciones completas. Es decir, .${\displaystyle x,y}$${\displaystyle \{E_{a}^{x}\}_{a},\{F_{b}^{y}\}_{b}}$${\displaystyle \sum _{a}E_{a}^{x}={\mathbb {I} }_{A},\sum _{b}F_{b}^{y}={\mathbb {I} }_{B}}$
2. ${\displaystyle P(a,b|x,y)=\left\langle \psi \right|E_{a}^{x}\otimes F_{b}^{y}\left|\psi \right\rangle }$, para todos .${\displaystyle a,b,x,y}$

En lo sucesivo, el conjunto de tales cajas se llamará . A diferencia del conjunto clásico de correlaciones, cuando se ve en el espacio de probabilidad, no es un politopo. Por el contrario, contiene límites tanto rectos como curvos. ^[40] Además, no es cerrado: ^[41] esto significa que existen cajas que pueden ser arbitrariamente bien aproximadas por sistemas cuánticos pero que en sí mismas no son cuánticas.${\displaystyle Q}$${\displaystyle Q}$${\displaystyle Q}$${\displaystyle P(a,b|x,y)}$

En la definición anterior, la separación espacial de las dos partes que llevan a cabo el experimento de Bell se modeló imponiendo que sus álgebras de operadores asociadas actúan sobre diferentes factores del espacio de Hilbert general que describe el experimento. Alternativamente, se podría modelar la separación espacial imponiendo que estas dos álgebras conmutan. Esto conduce a una definición diferente:${\displaystyle H_{A},H_{B}}$${\displaystyle H=H_{A}\otimes H_{B}}$

${\displaystyle P(a,b|x,y)}$admite una realización cuántica de campo si y sólo si existe un espacio de Hilbert , un vector normalizado y operadores de proyección tales que${\displaystyle H}$${\displaystyle \left|\psi \right\rangle \in H}$${\displaystyle E_{a}^{x}:H\to H,F_{b}^{y}:H\to H}$

1. Para todos los , los conjuntos representan mediciones completas. Es decir, .${\displaystyle x,y}$${\displaystyle \{E_{a}^{x}\}_{a},\{F_{b}^{y}\}_{b}}$${\displaystyle \sum _{a}E_{a}^{x}={\mathbb {I} },\sum _{b}F_{b}^{y}={\mathbb {I} }}$
2. ${\displaystyle P(a,b|x,y)=\left\langle \psi \right|E_{a}^{x}F_{b}^{y}\left|\psi \right\rangle }$, para todos .${\displaystyle a,b,x,y}$
3. ${\displaystyle [E_{a}^{x},F_{b}^{y}]=0}$, para todos .${\displaystyle a,b,x,y}$

Llamemos al conjunto de todas estas correlaciones .${\displaystyle Q_{c}}$${\displaystyle P(a,b|x,y)}$

¿Cómo se relaciona este nuevo conjunto con el más convencional definido anteriormente? Se puede demostrar que es cerrado. Además, , donde denota el cierre de . El problema de Tsirelson ^[42] consiste en decidir si la relación de inclusión es estricta, es decir, si . Este problema solo aparece en dimensiones infinitas: cuando el espacio de Hilbert en la definición de está restringido a ser de dimensión finita, el cierre del conjunto correspondiente es igual a . ^[42]${\displaystyle Q}$${\displaystyle Q_{c}}$${\displaystyle {\bar {Q}}\subseteq Q_{c}}$${\displaystyle {\bar {Q}}}$${\displaystyle Q}$${\displaystyle {\bar {Q}}\subseteq Q_{c}}$${\displaystyle {\bar {Q}}=Q_{c}}$${\displaystyle H}$${\displaystyle Q_{c}}$${\displaystyle {\bar {Q}}}$

En enero de 2020, Ji, Natarajan, Vidick, Wright y Yuen afirmaron un resultado en la teoría de la complejidad cuántica ^[43] que implicaría que , resolviendo así el problema de Tsirelson. ^{[44] [45] [46] [47] [48] [49] [50]}${\displaystyle {\bar {Q}}\neq Q_{c}}$

El problema de Tsirelson puede demostrarse como equivalente al problema de incrustación de Connes , ^{[51] [52] [53]} una famosa conjetura en la teoría de las álgebras de operadores.

Dado que las dimensiones de y son, en principio, ilimitadas, determinar si una caja dada admite una realización cuántica es un problema complicado. De hecho, se sabe que el doble problema de establecer si una caja cuántica puede tener una puntuación perfecta en un juego no local es indecidible. ^[41] Además, el problema de decidir si puede ser aproximada por un sistema cuántico con precisión es NP-hard. ^[54] Caracterizar cajas cuánticas es equivalente a caracterizar el cono de matrices semidefinidas completamente positivas bajo un conjunto de restricciones lineales. ^[55]${\displaystyle H_{A}}$${\displaystyle H_{B}}$${\displaystyle P(a,b|x,y)}$${\displaystyle P(a,b|x,y)}$${\displaystyle 1/\operatorname {poly} (|X||Y|)}$

Para dimensiones fijas pequeñas , se puede explorar, utilizando métodos variacionales, si se puede realizar en un sistema cuántico bipartito , con , . Sin embargo, ese método solo se puede utilizar para demostrar la realizabilidad de , y no su irrealizabilidad con sistemas cuánticos.${\displaystyle d_{A},d_{B}}$${\displaystyle P(a,b|x,y)}$${\displaystyle H_{A}\otimes H_{B}}$${\displaystyle \dim(H_{A})=d_{A}}$${\displaystyle \dim(H_{B})=d_{B}}$${\displaystyle P(a,b|x,y)}$

Para demostrar la irrealizabilidad, el método más conocido es la jerarquía de Navascués–Pironio–Acín (NPA). ^[56] Esta es una secuencia infinita decreciente de conjuntos de correlaciones con las propiedades:${\displaystyle Q^{1}\supset Q^{2}\supset Q^{3}\supset ...}$

1. Si , entonces para todos .${\displaystyle P(a,b|x,y)\in Q_{c}}$${\displaystyle P(a,b|x,y)\in Q^{k}}$${\displaystyle k}$
2. Si , entonces existe tal que .${\displaystyle P(a,b|x,y)\not \in Q_{c}}$${\displaystyle k}$${\displaystyle P(a,b|x,y)\not \in Q^{k}}$
3. Para cualquier , decidir si se puede formular como un programa semidefinido .${\displaystyle k}$${\displaystyle P(a,b|x,y)\in Q^{k}}$

La jerarquía NPA proporciona, por tanto, una caracterización computacional, no de , sino de . Si , (como afirman Ji, Natarajan, Vidick, Wright y Yuen), entonces se necesita un nuevo método para detectar la no realizabilidad de las correlaciones en . Si el problema de Tsirelson se resolviera afirmativamente, es decir, , entonces los dos métodos anteriores proporcionarían una caracterización práctica de .${\displaystyle Q}$${\displaystyle Q_{c}}$${\displaystyle {\bar {Q}}\not =Q_{c}}$${\displaystyle Q_{c}-{\bar {Q}}}$${\displaystyle {\bar {Q}}=Q_{c}}$${\displaystyle {\bar {Q}}}$

Los trabajos mencionados anteriormente describen cómo es el conjunto cuántico de correlaciones, pero no explican por qué. ¿Son inevitables las correlaciones cuánticas, incluso en las teorías físicas postcuánticas, o, por el contrario, podrían existir correlaciones fuera de ellas que, sin embargo, no conduzcan a ningún comportamiento operativo no físico?${\displaystyle {\bar {Q}}}$

En su influyente artículo de 1994, Popescu y Rohrlich exploran si las correlaciones cuánticas pueden explicarse apelando únicamente a la causalidad relativista. ^[57] Es decir, si cualquier caja hipotética permitiría construir un dispositivo capaz de transmitir información a una velocidad superior a la de la luz. En el nivel de correlaciones entre dos partes, la causalidad de Einstein se traduce en el requisito de que la elección de medición de Alice no debería afectar las estadísticas de Bob, y viceversa. De lo contrario, Alice (Bob) podría enviarle una señal a Bob (Alice) instantáneamente al elegir su configuración de medición apropiadamente. Matemáticamente, las condiciones de no señalización de Popescu y Rohrlich son:${\displaystyle P(a,b|x,y)\not \in {\bar {Q}}}$${\displaystyle x}$ ${\displaystyle (y)}$$${\displaystyle \sum _{a}P(a,b|x,y)=\sum _{a}P(a,b|x^{\prime },y)=:P_{B}(b|y),}$$$${\displaystyle \sum _{b}P(a,b|x,y)=\sum _{b}P(a,b|x,y^{\prime })=:P_{A}(a|x).}$$

Al igual que el conjunto de cajas clásicas, cuando se representa en el espacio de probabilidad, el conjunto de cajas sin señalización forma un politopo . Popescu y Rohrlich identificaron una caja que, si bien cumple con las condiciones de no señalización, viola el límite de Tsirelson y, por lo tanto, es irrealizable en física cuántica. Denominada caja PR, se puede escribir como:${\displaystyle P(a,b|x,y)}$$${\displaystyle P(a,b|x,y)={\frac {1}{2}}\delta _{xy,a\oplus b}.}$$

Aquí se toman valores en , y denota la suma módulo dos. Se puede verificar que el valor CHSH de esta caja es 4 (en oposición al límite de Tsirelson de ). Esta caja había sido identificada anteriormente por Rastall ^[58] y Khalfin y Tsirelson . ^[59]${\displaystyle a,b,x,y}$${\displaystyle {0,1}}$${\displaystyle a\oplus b}$${\displaystyle 2{\sqrt {2}}\approx 2.828}$

En vista de este desajuste, Popescu y Rohrlich plantean el problema de identificar un principio físico, más fuerte que las condiciones de ausencia de señalización, que permita derivar el conjunto de correlaciones cuánticas. A continuación se formularon varias propuestas:

1. Complejidad de comunicación no trivial (NTCC). ^[60] Este principio estipula que las correlaciones no locales no deben ser tan fuertes como para permitir que dos partes resuelvan todos los problemas de comunicación unidireccional con cierta probabilidad utilizando solo un bit de comunicación. Se puede demostrar que cualquier caja que viole el límite de Tsirelson en más de es incompatible con NTCC.${\displaystyle p>1/2}$${\displaystyle 2{\sqrt {2}}\left({\frac {2}{\sqrt {3}}}-1\right)\approx 0.4377}$
2. Sin ventaja para el cálculo no local (NANLC). ^[61] Se considera el siguiente escenario: dada una función , se distribuyen las cadenas de bits a dos partes y se les pide que generen los bits de manera que sea una buena estimación para . El principio de NANLC establece que las cajas no locales no deberían dar a las dos partes ninguna ventaja para jugar este juego. Se ha demostrado que cualquier caja que viole el límite de Tsirelson proporcionaría dicha ventaja.${\displaystyle f_{0,1}^{n}\to 1}$${\displaystyle n}$${\displaystyle x,y}$${\displaystyle a,b}$${\displaystyle a\oplus b}$${\displaystyle f(x\oplus y)}$
3. Causalidad de la información (CI). ^[62] El punto de partida es un escenario de comunicación bipartita donde una de las partes (Alice) recibe una cadena aleatoria de bits. La segunda parte, Bob, recibe un número aleatorio . Su objetivo es transmitir a Bob el bit , para lo cual se permite a Alice transmitir bits a Bob. El principio de CI establece que la suma de la información mutua entre el bit de Alice y la estimación de Bob no puede exceder el número de bits transmitidos por Alice. Se muestra que cualquier caja que viole el límite de Tsirelson permitiría a dos partes violar la CI.${\displaystyle x}$${\displaystyle n}$${\displaystyle k\in \{1,...,n\}}$${\displaystyle x_{k}}$${\displaystyle s}$${\displaystyle k}$${\displaystyle s}$
4. Localidad macroscópica (ML). ^[63] En la configuración considerada, dos partes separadas realizan extensas mediciones de baja resolución sobre una gran cantidad de pares de partículas correlacionadas preparados independientemente. ML establece que cualquier experimento “macroscópico” de este tipo debe admitir un modelo de variable oculta local. Está demostrado que cualquier experimento microscópico capaz de violar el límite de Tsirelson también violaría la no localidad estándar de Bell cuando se lo lleva a la escala macroscópica. Además del límite de Tsirelson, el principio de ML recupera por completo el conjunto de todos los correladores cuánticos de dos puntos.
5. Ortogonalidad local (LO). ^[64] Este principio se aplica a escenarios de Bell multipartitos, donde las partes realizan respectivamente experimentos en sus laboratorios locales. Obtienen respectivamente los resultados . El par de vectores se denomina evento. Se dice que dos eventos , son localmente ortogonales si existe tal que y . El principio de LO establece que, para cualquier caja multipartita, la suma de las probabilidades de cualquier conjunto de eventos localmente ortogonales por pares no puede exceder 1. Está demostrado que cualquier caja bipartita que viole el límite de Tsirelson por una cantidad de viola LO.${\displaystyle n}$${\displaystyle x_{1},...,x_{n}}$${\displaystyle a_{1},...,a_{n}}$${\displaystyle ({\bar {a}}|{\bar {x}})}$${\displaystyle ({\bar {a}}|{\bar {x}})}$${\displaystyle ({\bar {a}}^{\prime }|{\bar {x}}^{\prime })}$${\displaystyle k}$${\displaystyle x_{k}=x_{k}^{\prime }}$${\displaystyle a_{k}\not =a_{k}^{\prime }}$${\displaystyle 0.052}$

Todos estos principios pueden ser refutados experimentalmente bajo el supuesto de que podemos decidir si dos o más eventos están separados por una distancia espacial. Esto distingue a este programa de investigación de la reconstrucción axiomática de la mecánica cuántica a través de las teorías probabilísticas generalizadas .

Los trabajos anteriores se basan en el supuesto implícito de que cualquier conjunto físico de correlaciones debe estar cerrado bajo conexiones. ^[65] Esto significa que cualquier caja efectiva construida mediante la combinación de las entradas y salidas de una serie de cajas dentro del conjunto considerado también debe pertenecer al conjunto. El cierre bajo conexiones no parece imponer ningún límite al valor máximo de CHSH. Sin embargo, no es un principio de vacío: por el contrario, en ^[65] se muestra que muchas familias simples e intuitivas de conjuntos de correlaciones en el espacio de probabilidad lo violan.

Originalmente, se desconocía si alguno de estos principios (o un subconjunto de ellos) era lo suficientemente fuerte como para derivar todas las restricciones que definen . Esta situación continuó durante algunos años hasta la construcción del conjunto casi cuántico . ^[66] es un conjunto de correlaciones que está cerrado bajo cableados y puede caracterizarse mediante programación semidefinida. Contiene todas las correlaciones en , pero también algunas cajas no cuánticas . Sorprendentemente, se ha demostrado que todas las cajas dentro del conjunto casi cuántico son compatibles con los principios de NTCC, NANLC, ML y LO. También hay evidencia numérica de que las cajas casi cuánticas también cumplen con IC. Parece, por lo tanto, que, incluso cuando se toman en conjunto los principios anteriores, no son suficientes para distinguir el conjunto cuántico en el escenario de Bell más simple de dos partes, dos entradas y dos salidas. ^[66]${\displaystyle {\bar {Q}}}$${\displaystyle {\tilde {Q}}}$ ${\displaystyle {\tilde {Q}}}$${\displaystyle Q_{c}\supset {\bar {Q}}}$${\displaystyle P(a,b|x,y)\not \in Q_{c}}$

La no localidad se puede aprovechar para llevar a cabo tareas de información cuántica que no dependen del conocimiento del funcionamiento interno de los aparatos de preparación y medición que intervienen en el experimento. La seguridad o fiabilidad de cualquier protocolo de este tipo depende únicamente de la solidez de las correlaciones medidas experimentalmente . Estos protocolos se denominan independientes del dispositivo.${\displaystyle P(a,b|x,y)}$

El primer protocolo independiente del dispositivo propuesto fue la distribución de clave cuántica independiente del dispositivo (QKD). ^[67] En esta primitiva, a dos partes distantes, Alice y Bob, se les distribuye un estado cuántico entrelazado, que sondean, obteniendo así las estadísticas . Basándose en lo no local que resulta ser la caja, Alice y Bob estiman cuánto conocimiento podría poseer un adversario cuántico externo, Eve (el espía), sobre el valor de las salidas de Alice y Bob. Esta estimación les permite idear un protocolo de reconciliación al final del cual Alice y Bob comparten un bloc de notas de un solo uso perfectamente correlacionado del que Eve no tiene información alguna. El bloc de notas de un solo uso puede entonces usarse para transmitir un mensaje secreto a través de un canal público. Aunque los primeros análisis de seguridad sobre QKD independiente del dispositivo se basaban en que Eve llevara a cabo una familia específica de ataques, ^[68] todos estos protocolos han demostrado recientemente ser incondicionalmente seguros. ^[69]${\displaystyle P(a,b|x,y)}$${\displaystyle P(a,b|x,y)}$

La no localidad se puede utilizar para certificar que los resultados de una de las partes en un experimento de Bell son parcialmente desconocidos para un adversario externo. Al introducir una semilla parcialmente aleatoria en varias cajas no locales y, después de procesar los resultados, se puede terminar con una cadena más larga (potencialmente ilimitada) de aleatoriedad comparable ^{[70] o con una cadena más corta pero más aleatoria [71]} . Esta última primitiva se puede demostrar imposible en un contexto clásico ^{[72] .}

La certificación, expansión y amplificación de la aleatoriedad independiente del dispositivo (DI) son técnicas que se utilizan para generar números aleatorios de alta calidad que sean seguros contra posibles ataques a los dispositivos subyacentes utilizados para generar números aleatorios. Estas técnicas tienen aplicaciones críticas en criptografía, donde los números aleatorios de alta calidad son esenciales para garantizar la seguridad de los protocolos criptográficos. La certificación de aleatoriedad es el proceso de verificar que la salida de un generador de números aleatorios es verdaderamente aleatoria y no ha sido alterada por un adversario. La certificación de aleatoriedad DI realiza esta verificación sin hacer suposiciones sobre los dispositivos subyacentes que generan números aleatorios. En cambio, la aleatoriedad se certifica observando correlaciones entre las salidas de diferentes dispositivos que se generan utilizando el mismo proceso físico. Investigaciones recientes han demostrado la viabilidad de la certificación de aleatoriedad DI utilizando sistemas cuánticos entrelazados, como fotones o electrones. La expansión de la aleatoriedad consiste en tomar una pequeña cantidad de semilla aleatoria inicial y expandirla en una secuencia mucho más grande de números aleatorios. En la expansión de aleatoriedad DI, la expansión se realiza utilizando mediciones de sistemas cuánticos que se preparan en un estado altamente entrelazado. La seguridad de la expansión está garantizada por las leyes de la mecánica cuántica, que hacen imposible que un adversario prediga el resultado de la expansión. Investigaciones recientes han demostrado que la expansión de aleatoriedad DI se puede lograr utilizando pares de fotones entrelazados y dispositivos de medición que violan una desigualdad de Bell. ^[73] La amplificación de aleatoriedad es el proceso de tomar una pequeña cantidad de semilla aleatoria inicial y aumentar su aleatoriedad utilizando un algoritmo criptográfico. En la amplificación de aleatoriedad DI, este proceso se realiza utilizando propiedades de entrelazamiento y mecánica cuántica. La seguridad de la amplificación está garantizada por el hecho de que cualquier intento por parte de un adversario de manipular el resultado del algoritmo inevitablemente introducirá errores que pueden detectarse y corregirse. Investigaciones recientes han demostrado la viabilidad de la amplificación de aleatoriedad DI utilizando entrelazamiento cuántico y la violación de una desigualdad de Bell. ^[74]

La certificación, expansión y amplificación de la aleatoriedad DI son técnicas poderosas para generar números aleatorios de alta calidad que son seguros contra cualquier ataque potencial a los dispositivos subyacentes utilizados para generar números aleatorios. Estas técnicas tienen aplicaciones críticas en criptografía y es probable que se vuelvan cada vez más cruciales a medida que avanza la tecnología de computación cuántica. Además, existe un enfoque más suave llamado semi-DI donde los números aleatorios se pueden generar con algunas suposiciones sobre el principio de funcionamiento de los dispositivos, el entorno, la dimensión, la energía, etc., en el que se beneficia de la facilidad de implementación y la alta tasa de generación. ^[75]

A veces, la caja compartida por Alice y Bob es tal que solo admite una única realización cuántica. Esto significa que existen operadores de medición y un estado cuántico que da lugar a tal que cualquier otra realización física de está conectada a través de transformaciones unitarias locales. Este fenómeno, que puede interpretarse como un ejemplo de tomografía cuántica independiente del dispositivo, fue señalado por primera vez por Tsirelson ^[40] y denominado autoprueba por Mayers y Yao. ^[67] Se sabe que la autoprueba es robusta frente al ruido sistemático, es decir, si las estadísticas medidas experimentalmente son lo suficientemente cercanas a , aún se pueden determinar el estado subyacente y los operadores de medición hasta las barras de error. ^[67]${\displaystyle P(a,b|x,y)}$${\displaystyle E_{a}^{x},F_{b}^{y}}$${\displaystyle \left|\psi \right\rangle }$${\displaystyle P(a,b|x,y)}$${\displaystyle {\tilde {E}}_{a}^{x},{\tilde {F}}_{b}^{y},\left|{\tilde {\psi }}\right\rangle }$${\displaystyle P(a,b|x,y)}$${\displaystyle E_{a}^{x},F_{b}^{y},\left|\psi \right\rangle }$${\displaystyle P(a,b|x,y)}$

El grado de no localidad de una caja cuántica también puede proporcionar límites inferiores en la dimensión del espacio de Hilbert de los sistemas locales accesibles a Alice y Bob. ^[76] Este problema es equivalente a decidir la existencia de una matriz con un rango semidefinido completamente positivo bajo. ^[77] Encontrar límites inferiores en la dimensión del espacio de Hilbert basándose en estadísticas resulta ser una tarea difícil, y los métodos generales actuales solo proporcionan estimaciones muy bajas. ^[78] Sin embargo, un escenario de Bell con cinco entradas y tres salidas es suficiente para proporcionar límites inferiores arbitrariamente altos en la dimensión del espacio de Hilbert subyacente. ^[79] Los protocolos de comunicación cuántica que suponen un conocimiento de la dimensión local de los sistemas de Alice y Bob, pero que por lo demás no hacen afirmaciones sobre la descripción matemática de los dispositivos de preparación y medición involucrados se denominan protocolos semiindependientes del dispositivo. Actualmente, existen protocolos semiindependientes del dispositivo para la distribución de claves cuánticas ^[80] y la expansión de aleatoriedad. ^[81]${\displaystyle P(a,b|x,y)}$

• Acción a distancia
• El experimento de Popper
• Pseudotelepatía cuántica
• Contextualidad cuántica
• Fundamentos cuánticos

• Grib, AA; Rodrigues, WA (1999). No localidad en física cuántica . Springer Verlag. ISBN 978-0-306-46182-8.
• Cramer, JG (2015). El apretón de manos cuántico: entrelazamiento, no localidad y transacciones . Springer Verlag. ISBN 978-3-319-24642-0.
• Duarte, FJ (2019). Fundamentos del entrelazamiento cuántico . Instituto de Física (Reino Unido). ISBN 978-0-7503-2226-3.