Principio de localidad

En física , el principio de localidad establece que un objeto se ve influido directamente solo por su entorno inmediato. Una teoría que incluye el principio de localidad se denomina "teoría local". Esta es una alternativa al concepto de acción instantánea o "no local" a distancia . La localidad evolucionó a partir de las teorías de campo de la física clásica . La idea es que para que una causa en un punto tenga un efecto en otro punto, algo en el espacio entre esos puntos debe mediar la acción. Para ejercer una influencia, algo, como una onda o una partícula, debe viajar a través del espacio entre los dos puntos, llevando la influencia.

La teoría especial de la relatividad limita la velocidad máxima a la que puede viajar la influencia causal a la velocidad de la luz , . Por lo tanto, el principio de localidad implica que un evento en un punto no puede causar un resultado verdaderamente simultáneo en otro punto. Un evento en el punto no puede causar un resultado en el punto en un tiempo menor que , donde es la distancia entre los puntos y es la velocidad de la luz en el vacío.${\estilo de visualización c}$${\estilo de visualización A}$${\estilo de visualización B}$${\displaystyle T=D/c}$${\estilo de visualización D}$${\estilo de visualización c}$

El principio de localidad desempeña un papel fundamental en uno de los resultados centrales de la mecánica cuántica. En 1935, Albert Einstein , Boris Podolsky y Nathan Rosen , con su experimento mental de la paradoja EPR , plantearon la posibilidad de que la mecánica cuántica no fuera una teoría completa. Describieron dos sistemas separados físicamente después de interactuar; este par se llamaría entrelazado en la terminología moderna. Razonaron que sin adiciones, ahora llamadas variables ocultas , la mecánica cuántica predeciría relaciones ilógicas entre las mediciones separadas físicamente.

En 1964, John Stewart Bell formuló el teorema de Bell , una desigualdad que, si se viola en experimentos reales, implica que la mecánica cuántica viola la causalidad local (denominada realismo local en trabajos posteriores), un resultado que ahora se considera equivalente a excluir las variables ocultas locales . Las variaciones progresivas de esos experimentos de prueba de Bell han demostrado desde entonces que la mecánica cuántica viola ampliamente las desigualdades de Bell. Según algunas interpretaciones de la mecánica cuántica , este resultado implica que algunos efectos cuánticos violan el principio de localidad.

Durante el siglo XVII, el principio de gravitación universal de Newton se formuló en términos de "acción a distancia", violando así el principio de localidad. El propio Newton consideró que esta violación era absurda:

Es inconcebible que la materia inanimada pueda, sin la mediación de algo más que no sea material, operar sobre otra materia y afectarla sin contacto mutuo… Que la gravedad sea innata, inherente y esencial a la materia, de modo que un cuerpo pueda actuar sobre otro a distancia a través del vacío, sin la mediación de ninguna otra cosa, por medio de la cual su acción y fuerza puedan transmitirse de uno a otro, es para mí un absurdo tan grande que creo que ningún hombre que tenga una facultad competente de pensamiento en materia filosófica puede caer jamás en él. La gravedad debe ser causada por un agente que actúe constantemente de acuerdo con ciertas leyes; pero el que este agente sea material o inmaterial, lo he dejado a la consideración de mis lectores. ^[1]

—  Isaac Newton, Cartas a Bentley , 1692/3

La ley de Coulomb de las fuerzas eléctricas fue inicialmente formulada también como una acción instantánea a distancia, pero en 1880, James Clerk Maxwell demostró que las ecuaciones de campo , que obedecen a la localidad, predicen todos los fenómenos del electromagnetismo. ^{[ cita requerida ]} Estas ecuaciones muestran que las fuerzas electromagnéticas se propagan a la velocidad de la luz.

En 1905, la teoría especial de la relatividad de Albert Einstein postuló que ninguna materia o energía puede viajar más rápido que la velocidad de la luz, y con ello Einstein buscó reformular la física de una manera que obedeciera al principio de localidad. Más tarde logró producir una teoría alternativa de la gravitación, la relatividad general , que obedece al principio de localidad.

Sin embargo, un desafío diferente al principio de localidad se desarrolló posteriormente a partir de la teoría de la mecánica cuántica , que el propio Einstein había ayudado a crear.

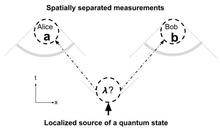
Los diagramas de espacio-tiempo simples pueden ayudar a aclarar las cuestiones relacionadas con la localidad. ^[2] Una forma de describir las cuestiones de localidad adecuadas para la discusión de la mecánica cuántica se ilustra en el diagrama. Una partícula se crea en una ubicación, luego se divide y se mide en otras dos ubicaciones separadas espacialmente. Las dos mediciones se nombran para Alice y Bob. Alice realiza mediciones (A) y obtiene un resultado ); Bob realiza ( ) y obtiene el resultado . El experimento se repite muchas veces y se comparan los resultados.${\displaystyle \mathbf {a}}$${\estilo de visualización B}$${\displaystyle \mathbf {b}}$

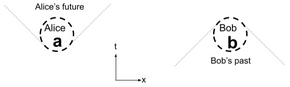
Un diagrama de espacio-tiempo tiene una coordenada de tiempo que va vertical y una coordenada de espacio que va horizontal. Alice, en una región local a la izquierda, puede afectar eventos solo en un cono que se extiende en el futuro como se muestra; la velocidad finita de la luz le impide afectar otras áreas, incluida la ubicación de Bob en este caso. De manera similar, podemos usar el diagrama para razonar que las circunstancias locales de Bob no pueden ser alteradas por Alice al mismo tiempo: todos los eventos que causan un efecto en Bob están en el cono debajo de su ubicación en el diagrama. Las líneas discontinuas alrededor de Alice muestran sus ubicaciones futuras válidas; las líneas discontinuas alrededor de Bob muestran eventos que podrían haber causado su circunstancia actual. Cuando Alice mide estados cuánticos en su ubicación, obtiene los resultados etiquetados ; de manera similar, Bob obtiene . Los modelos de localidad intentan explicar la relación estadística entre estos valores medidos. ${\displaystyle \mathbf {a}}$${\displaystyle \mathbf {b}}$

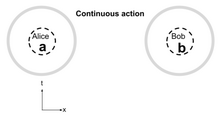
El modelo de localidad más simple es el de no localidad: acción instantánea a distancia sin límites para la relatividad. El modelo de localidad para la acción a distancia se llama acción continua . ^[2] El área gris (un círculo aquí) es un concepto matemático llamado "pantalla". Cualquier camino desde una ubicación a través de la pantalla se convierte en parte del modelo físico en esa ubicación. El anillo gris indica que los eventos de todas las partes del espacio y el tiempo pueden afectar la probabilidad medida por Alice o Bob. Entonces, en el caso de la acción continua, los eventos en todos los tiempos y lugares afectan el modelo de Alice y Bob. Este modelo simple es muy exitoso para la dinámica planetaria solar con gravedad newtoniana y en electrostática, casos donde los efectos relativistas son insignificantes.

Muchos modelos de localidad ignoran explícita o implícitamente el posible efecto de los eventos futuros. El diagrama de espacio-tiempo de la derecha muestra el efecto de dicha restricción cuando se combina con una acción continua. Las entradas provenientes del futuro (por encima de la línea discontinua) ya no se consideran parte del modelo de Alice o Bob. Al comparar este diagrama con el de la acción continua, queda claro que no se trata del mismo modelo de localidad. ^[2] Los argumentos de sentido común sobre que el futuro no afecta al presente son criterios razonables, pero tales suposiciones alteran el carácter matemático de los modelos.

John Stewart Bell, al analizar su teorema de Bell, utiliza el modelo de cribado que se muestra a la derecha. Los eventos en el pasado común de Alice y Bob son parte del modelo utilizado para calcular las probabilidades de Alice y Bob, como lo indica la forma en que la pantalla absorbe esos eventos. Sin embargo, se excluyen los eventos en la ubicación de Bob durante la medición de Alice y los eventos en el futuro. Bell llamó a esta suposición causalidad local , pero con el diagrama podemos razonar sobre el significado de la suposición sin confundirnos con otros significados de local combinados con otros significados de causal. ^[2] Las líneas discontinuas muestran regiones relativísticamente válidas en el pasado de Alice o Bob. El arco gris es la supuesta "pantalla" de Bell.

Las posiciones relativas de nuestros pocos planetas, fácilmente distinguibles (por ejemplo) se pueden ver directamente: comprender y medir su ubicación relativa solo plantea problemas técnicos. El mundo submicroscópico, por otro lado, se conoce solo mediante mediciones que promedian muchos eventos aparentemente aleatorios ("estadísticos" o "probabilísticos") y las mediciones pueden mostrar resultados similares a partículas o a ondas según su diseño. Este mundo está gobernado por la mecánica cuántica . ^[3] Los conceptos de localidad son más complejos y se describen en el lenguaje de la probabilidad y la correlación .

En el artículo de 1935 sobre la paradoja de Einstein-Podolsky-Rosen (artículo EPR), ^[4] Albert Einstein , Boris Podolsky y Nathan Rosen imaginaron un experimento de este tipo. Observaron que la mecánica cuántica predice lo que ahora se conoce como entrelazamiento cuántico y examinaron sus consecuencias. ^[5] En su opinión, el principio clásico de localidad implicaba que "no puede producirse ningún cambio real" en el sitio de Bob como resultado de las mediciones que Alice estaba realizando. Dado que la mecánica cuántica predice un colapso de la función de onda que depende de la elección de la medición de Bob, concluyeron que se trataba de una forma de acción a distancia y que la función de onda no podía ser una descripción completa de la realidad. Otros físicos no estuvieron de acuerdo: aceptaron la función de onda cuántica como completa y cuestionaron la naturaleza de la localidad y la realidad asumidas en el artículo EPR. ^[6]

En 1964, John Stewart Bell investigó si sería posible cumplir el objetivo de Einstein (completar la teoría cuántica) con variables ocultas locales para explicar las correlaciones entre partículas separadas espacialmente, tal como predice la teoría cuántica. Bell estableció un criterio para distinguir entre la teoría de variables ocultas locales y la teoría cuántica midiendo valores específicos de correlaciones entre partículas entrelazadas. Pruebas experimentales posteriores han demostrado que algunos efectos cuánticos violan las desigualdades de Bell y no pueden ser reproducidos por una teoría de variables ocultas locales. ^[5] El teorema de Bell depende de modelos de localidad cuidadosamente definidos.

Bell describió la causalidad local en términos de probabilidad necesaria para el análisis de la mecánica cuántica. Utilizando la notación que para la probabilidad de un resultado con un estado dado , Bell investigó la distribución de probabilidad donde representa variables de estado ocultas establecidas (localmente) cuando las dos partículas están inicialmente co-ubicadas. Si la causalidad local se cumple, entonces las probabilidades observadas por Alice y por Bob deberían estar acopladas únicamente por las variables ocultas, y podemos demostrar que Bell demostró que una consecuencia de esta factorización son límites en las correlaciones observadas por Alice y Bob conocidas como desigualdades de Bell. Dado que la mecánica cuántica predice correlaciones más fuertes que este límite, no se pueden agregar variables ocultas establecidas localmente para "completar" la teoría cuántica como lo desea el artículo de EPR. ^[7]${\displaystyle P(\mathbf {r} |g)}$${\displaystyle \mathbf {r}}$${\estilo de visualización g}$$${\displaystyle P(\mathbf {ab} |AB,\lambda )}$$${\estilo de visualización \lambda}$$${\displaystyle P(\mathbf {ab} |AB,\lambda )=P(\mathbf {a} |A,\lambda )P(\mathbf {b} |B,\lambda ),}$$

Numerosos experimentos diseñados específicamente para investigar las cuestiones de localidad confirman las predicciones de la mecánica cuántica; estos incluyen experimentos en los que las dos ubicaciones de medición están separadas por más de un kilómetro. ^{[7] [8]} El Premio Nobel de Física de 2022 fue otorgado a Alain Aspect , John Clauser y Anton Zeilinger , en parte "por experimentos con fotones entrelazados, que establecieron la violación de las desigualdades de Bell". ^[9] El aspecto específico de la teoría cuántica que conduce a estas correlaciones se denomina entrelazamiento cuántico y ahora se utilizan versiones del escenario de Bell para verificar el entrelazamiento experimentalmente. ^[7]

Los resultados matemáticos de Bell, cuando se comparan con los datos experimentales, eliminan las teorías matemáticas cuánticas de variable oculta local. Pero la interpretación de las matemáticas con respecto al mundo físico sigue siendo objeto de debate. Bell describió las suposiciones en las que se basa su trabajo como "causalidad local", abreviada como "localidad"; autores posteriores se refirieron a las suposiciones como realismo local . ^[10] Estos nombres diferentes no alteran las suposiciones matemáticas.

Una revisión de artículos ^[11] que utilizan esta frase sugiere que una definición común (clásica) de física del realismo es

la suposición de que los resultados de las mediciones están bien definidos antes de las mediciones y son independientes de ellas. ^[12]

Esta definición incluye conceptos clásicos como "bien definido", que entra en conflicto con la superposición cuántica , y "antes de... las mediciones", que implica la preexistencia (metafísica) de propiedades. En concreto, el término realismo local en el contexto del teorema de Bell no puede verse como un tipo de "realismo" que implique localidad distinta del tipo implicado por el supuesto de cribado de Bell. Este conflicto entre las ideas comunes del realismo y la mecánica cuántica requiere un análisis cuidadoso siempre que se discuta el realismo local. ^{[11] : 98} Añadir un modificador de "localidad", que los resultados de dos mediciones bien separadas espacialmente no pueden afectarse causalmente entre sí, ^[5] no hace que la combinación se relacione con la prueba de Bell; la única interpretación que Bell asumió fue la que llamó causalidad local. ^{[11] : 98} En consecuencia, el teorema de Bell no restringe la posibilidad de variables no locales, así como las teorías basadas en la retrocausalidad o el superdeterminismo . ^[2]

Debido a la naturaleza probabilística del colapso de la función de onda, esta aparente violación de la localidad en la mecánica cuántica no puede usarse para transmitir información más rápido que la luz, de acuerdo con el teorema de no comunicación . ^[13] Asher Peres distingue entre no localidad débil y fuerte , esta última refiriéndose a las teorías que permiten la comunicación más rápida que la luz. Bajo estos términos, la mecánica cuántica permitiría correlaciones débilmente no locales pero no fuertes no localidades. ^[14]

Uno de los principios fundamentales de la teoría cuántica de campos es el principio de localidad. ^[15] Los operadores de campo y la densidad lagrangiana que describe la dinámica de los campos son locales, en el sentido de que las interacciones no se describen mediante acciones a distancia. Esto se puede lograr evitando términos en el lagrangiano que sean productos de dos campos que dependen de coordenadas distantes. ^{[15] [16]} Específicamente, en la teoría cuántica de campos relativista, para hacer cumplir los principios de localidad y causalidad se requiere la siguiente condición: si hay dos observables , cada uno localizado dentro de dos regiones espacio-temporales distintas que se encuentran a una separación espacial entre sí, los observables deben conmutar . Esta condición a veces se impone como uno de los axiomas de la teoría cuántica de campos relativista. ^{[15] [17]}

Wikiquote tiene citas relacionadas con Principio de localidad .

• No localidad cuántica frente a localidad de Einstein por H. Dieter Zeh