5 celdas truncadas

5 celdas	5 celdas truncadas	Bittruncadas de 5 celdas
Diagramas de Schlegel centrados en [3,3] (celdas opuestas en [3,3])

En geometría , un politopo truncado de 5 celdas es un politopo uniforme de 4 dimensiones ( politopo uniforme de 4 dimensiones ) formado como el truncamiento del politopo regular de 5 celdas .

Hay dos grados de truncamiento, incluido un truncamiento de bits .

5 celdas truncadas

5 celdas truncadas
Diagrama de Schlegel ( células tetraédricas visibles)
Tipo	Politopo 4 uniforme
Símbolo de Schläfli	t0,1 {3,3,3} t _{ 3,3,3}
Diagrama de Coxeter
Células	10	5 ( 3.3.3 ) 5 ( 3.6.6 )
Caras	30	20 {3} 10 {6}
Bordes	40
Vértices	20
Figura de vértice	Pirámide triangular equilátera
Grupo de simetría	A ₄ , [3,3,3], orden 120
Propiedades	convexo , isogonal
Índice uniforme	2 3 4

El pentacoron truncado de cinco celdas , pentacoron truncado o 4-símplex truncado está limitado por diez celdas : cinco tetraedros y cinco tetraedros truncados . Cada vértice está rodeado por tres tetraedros truncados y un tetraedro; la figura del vértice es un tetraedro alargado.

Construcción

La celda truncada de 5 elementos se puede construir a partir de la celda 5 truncando sus vértices en 1/3 de la longitud de su arista. Esto transforma las 5 celdas tetraédricas en tetraedros truncados e introduce 5 nuevas celdas tetraédricas ubicadas cerca de los vértices originales.

Estructura

Los tetraedros truncados están unidos entre sí por sus caras hexagonales y a los tetraedros por sus caras triangulares.

Visto en una matriz de configuración , se muestran todos los recuentos de incidencia entre elementos. Los números del vector f diagonal se derivan a través de la construcción de Wythoff , dividiendo el orden de grupo completo de un orden de subgrupo eliminando un espejo a la vez. ^[1]

Un ₄	k -cara	_por favor	o0	el ₁		el ₂		F3		k -figura	Notas
Un ₂	( )	o0	20	1	3	3	3	3	1	{3}v( )	Un ₄ /Un ₂ = 5!/3! = 20
Un ₂ Un ₁	{ }	el ₁	2	10	*	3	0	3	0	{3}	Un ₄ /Un ₂ Un ₁ = 5!/3!/2 = 10
Un ₁ Un ₁	{ }	el ₁	2	*	30	1	2	2	1	{ }v( )	Un ₄ / Un ₁ Un ₁ = 5!/2/2 = 30
Un ₂ Un ₁	el{3}	el ₂	6	3	3	10	*	2	0	{ }	Un ₄ /Un ₂ Un ₁ = 5!/3!/2 = 10
Un ₂	{3}	el ₂	3	0	3	*	20	1	1	{ }	Un ₄ /Un ₂ = 5!/3! = 20
Un ₃	t{3,3}	F3	12	6	12	4	4	5	*	( )	Un ₄ /Un ₃ = 5!/4! = 5
Un ₃	{3,3}	F3	4	0	6	0	4	*	5	( )	Un ₄ /Un ₃ = 5!/4! = 5

Proyecciones

La proyección del diagrama de Schlegel del tetraedro truncado primero de la celda 5 truncada en el espacio tridimensional tiene la siguiente estructura:

La envolvente de proyección es un tetraedro truncado .
Una de las celdas tetraédricas truncadas se proyecta sobre toda la envoltura.
Una de las celdas tetraédricas se proyecta sobre un tetraedro situado en el centro de la envoltura.
Cuatro tetraedros aplanados están unidos a las caras triangulares de la envoltura y conectados al tetraedro central a través de cuatro aristas radiales. Éstas son las imágenes de las cuatro celdas tetraédricas restantes.
Entre el tetraedro central y las 4 caras hexagonales de la envoltura hay 4 volúmenes tetraédricos truncados irregulares, que son las imágenes de las 4 celdas tetraédricas truncadas restantes.

Esta disposición de celdas en la proyección es análoga a la disposición de las caras en la proyección de caras primero del tetraedro truncado en el espacio bidimensional. La celda truncada de cinco elementos es el análogo en cuatro dimensiones del tetraedro truncado.

Imágenes

proyecciones ortográficas
Un _avión de Coxeter	Un ₄	Un ₃	Un ₂
Gráfico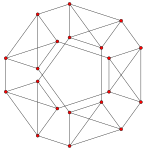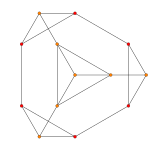
Simetría diedral	[5]	[4]	[3]

neto
proyección estereográfica
(centrada en el tetraedro truncado )

Nombres alternativos

Pentatopo truncado
4-símplex truncado
Pentacoron truncado (Acrónimo: tip) (Jonathan Bowers)

Coordenadas

Las coordenadas cartesianas para los vértices de un sistema truncado de 5 celdas centrado en el origen que tiene una longitud de arista de 2 son:

\left({\frac {3}{\sqrt {10}}},\ {\sqrt {3 \sobre 2}},\ \pm {\sqrt {3}},\ \pm 1\right)

\left({\frac {3}{\sqrt {10}}},\ {\sqrt {3 \sobre 2}},\ 0,\ ​​\pm 2\right)

\left({\frac {3}{\sqrt {10}}},\ {\frac {-1}{\sqrt {6}}},\ {\frac {2}{\sqrt {3}}},\ \pm 2\right)

\left({\frac {3}{\sqrt {10}}},\ {\frac {-1}{\sqrt {6}}},\ {\frac {-4}{\sqrt {3}}},\ 0\right)

\left({\frac {3}{\sqrt {10}}},\ {\frac {-5}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)

\left({\frac {3}{\sqrt {10}}},\ {\frac {-5}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)

\left(-{\sqrt {2 \sobre 5}},\ {\sqrt {2 \sobre 3}},\ {\frac {2}{\sqrt {3}}},\ \pm 2\right)

\left(-{\sqrt {2 \sobre 5}},\ {\sqrt {2 \sobre 3}},\ {\frac {-4}{\sqrt {3}}},\ 0\right)

\left(-{\sqrt {2 \sobre 5}},\ -{\sqrt {6}},\ 0,\ ​​0\right)

\left({\frac {-7}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)

\left({\frac {-7}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)

\left({\frac {-7}{\sqrt {10}}},\ -{\sqrt {3 \sobre 2}},\ 0,\ ​​0\right)

En términos más simples, los vértices de la celda truncada de 5 elementos se pueden construir en un hiperplano en el espacio de 5 elementos como permutaciones de (0,0,0,1,2) o de (0,1,2,2,2). Estas coordenadas provienen de facetas ortantes positivas del pentacruz truncado y del penteracto bitruncado respectivamente.

Politopos relacionados

La envoltura convexa del quinquenio truncado y su dual (asumiendo que son congruentes) es un policoron no uniforme compuesto por 60 celdas: 10 tetraedros , 20 octaedros (como antiprismas triangulares), 30 tetraedros (como difenoides tetragonales) y 40 vértices. Su figura de vértice es una cúpula hexaquistriangular .

Figura de vértice

Bittruncadas de 5 celdas

Bittruncadas de 5 celdas
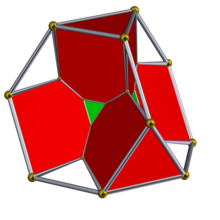Diagrama de Schlegel con celdas alternas ocultas.
Tipo	Politopo 4 uniforme
Símbolo de Schläfli	t1,2 {3,3,3} _2t {3,3,3}
Diagrama de Coxeter	oo
Células	10 ( 3.6.6 )
Caras	40	20 {3} 20 {6}
Bordes	60
Vértices	30
Figura de vértice	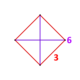( { }v{ } )
politopo dual	Disfenoidal de 30 células
Grupo de simetría	Aut (A ₄ ), [[3,3,3]], orden 240
Propiedades	convexo , isogonal , isotoxal , isocórico
Índice uniforme	5 6 7

El bitruncado de 5 celdas (también llamado pentacoronte bitruncado , decacoronte y de 10 celdas ) es un politopo de 4 dimensiones , o 4-politopo , compuesto por 10 celdas en forma de tetraedros truncados .

Topológicamente, bajo su simetría más alta, [[3,3,3]], existe una única forma geométrica, que contiene 10 tetraedros truncados uniformes. Los hexágonos son siempre regulares debido a la simetría de inversión del policoronte, de la cual el hexágono regular es el único caso entre los ditrígonos (un hexágono isogonal con simetría triple).

EL Elte lo identificó en 1912 como un politopo semirregular.

Cada cara hexagonal del tetraedro truncado está unida en orientación complementaria al tetraedro truncado vecino. Cada arista es compartida por dos hexágonos y un triángulo. Cada vértice está rodeado por 4 celdas tetraédricas truncadas en una figura de vértice difenoide tetragonal .

El 5-cell bitruncado es la intersección de dos pentágonos en configuración dual. Como tal, es también la intersección de un penteracto con el hiperplano que biseca la diagonal larga del penteracto ortogonalmente. En este sentido es un análogo de 4 dimensiones del octaedro regular (intersección de tetraedros regulares en configuración dual / bisección de teseracto en la diagonal larga) y el hexágono regular (triángulos equiláteros / cubo). El análogo de 5 dimensiones es el 5-símplex birectificado , y el análogo de - dimensiones es el politopo cuyo diagrama de Coxeter-Dynkin es lineal con anillos en el nodo o los dos nodos del medio. ${\estilo de visualización n}$

El bitruncado de 5 celdas es uno de los dos politopos de 4 celdas uniformes convexos no regulares que son transitivos entre celdas . El otro es el bitruncado de 24 celdas , que está compuesto por 48 cubos truncados.

Simetría

Este 4-politopo tiene una simetría pentacórica extendida superior (2×A ₄ , [[3,3,3]]), duplicada hasta el orden 240, porque el elemento correspondiente a cualquier elemento de la 5-celda subyacente puede intercambiarse con uno de los correspondientes a un elemento de su dual.

Nombres alternativos

Bitruncado de 5 celdas ( Norman W. Johnson )
10 células como un 4-politopo transitivo celular
Pentacoron bitruncado
Pentatopo bitruncado
4-símplex bitruncado
Decachoron (Acrónimo: deca) (Jonathan Bowers)

Imágenes

proyecciones ortográficas
Un _avión de Coxeter	Un ₄	Un ₃	Un ₂
Gráfico
Simetría diedral	[[5]] = [10]	[4]	[[3]] = [6]

Proyección estereográfica de un politopo esférico de 4 caras (centrado en una cara hexagonal)	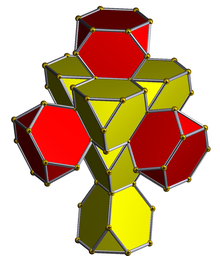Red (politopo)

Coordenadas

Las coordenadas cartesianas de un sistema bitruncado de 5 celdas centrado en el origen que tiene una longitud de arista de 2 son:

Coordenadas
$\pm \left({\sqrt {\frac {5}{2}}},\ {\frac {5}{\sqrt {6}}},\ {\frac {2}{\sqrt {3}}},\ 0\right)$ $\pm \left({\sqrt {\frac {5}{2}}},\ {\frac {5}{\sqrt {6}}},\ {\frac {-1}{\sqrt {3}}},\ \pm 1\right)$ $\pm \left({\sqrt {\frac {5}{2}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {4}{\sqrt {3}}},\ 0\right)$ $\pm \left({\sqrt {\frac {5}{2}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ \pm 2\right)$	$\pm \left({\sqrt {\frac {5}{2}}},\ -{\sqrt {\frac {3}{2}}},\ \pm {\sqrt {3}},\ \pm 1\right)$ $\pm \left({\sqrt {\frac {5}{2}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ \pm 2\right)$ $\pm \left(0,\ 2{\sqrt {\frac {2}{3}}},\ {\frac {4}{\sqrt {3}}},\ 0\right)$ $\pm \left(0,\ 2{\sqrt {\frac {2}{3}}},\ {\frac {-2}{\sqrt {3}}},\ \pm 2\right)$

De manera más simple, los vértices de la celda de 5 bits truncados se pueden construir en un hiperplano en el espacio de 5 bits como permutaciones de (0,0,1,2,2). Estas representan facetas ortantes positivas del pentacruz de bits truncado . Otra construcción en el espacio de 5 bits, centrada en el origen, son las 20 permutaciones de (-1,-1,0,1,1).

Politopos relacionados

La celda 5 bitruncada se puede ver como la intersección de dos celdas 5 regulares en posiciones duales.=∩.

Símplices truncados uniformes isotópicos
Oscuro.	2	3	4	5	6	7	8
Nombre Coxeter	Hexágono = t{3} = {6}	Octaedro = r{3,3} = {3 ^1,1 } = {3,4} $\left\{{\begin{array}{l}3\\3\end{array}}\right\}$	Decachoron 2t{3 ³ }	Dodecaterón 2r{3 ⁴ } = {3 ^2,2 } $\left\{{\begin{array}{l}3,3\\3,3\end{array}}\right\}$	Tetradecapetona 3t{3 ⁵ }	Hexadecaexón 3r{3 ⁶ } = {3 ^3,3 } $\left\{{\begin{array}{l}3,3,3\\3,3,3\end{array}}\right\}$	Octadecazetona 4t{3 ⁷ }
Imágenes
Figura de vértice	( )∨( )	{ }×{ }	{ }∨{ }	{3}×{3}	{3}∨{3}	{3,3}×{3,3}	{3,3}∨{3,3}
Facetas		{3}	t{3,3}	r{3,3,3}	2t{3,3,3,3}	2r{3,3,3,3,3}	3t{3,3,3,3,3,3}
Como simplex duales que se intersectan	∩	∩	∩	∩	∩	∩	∩

Configuración

Visto en una matriz de configuración , se muestran todos los recuentos de incidencia entre elementos. Los números del vector f diagonal se derivan a través de la construcción de Wythoff , dividiendo el orden de grupo completo de un orden de subgrupo eliminando un espejo a la vez. ^[2]

_por favor	o0	el ₁		el ₂			F3
o0	30	2	2	1	4	1	2	2
el ₁	2	30	*	1	2	0	2	1
el ₁	2	*	30	0	2	1	1	2
el ₂	3	3	0	10	*	*	2	0
	6	3	3	*	20	*	1	1
	3	0	3	*	*	10	0	2
F3	12	12	6	4	4	0	5	*
F3	12	6	12	0	4	4	*	5

Poliedro oblicuo regular relacionado

El poliedro oblicuo regular , {6,4|3}, existe en el espacio 4 con 4 hexágonos alrededor de cada vértice, en una figura de vértices no plana en zigzag. Estas caras hexagonales se pueden ver en la celda de 5 bitruncada, utilizando las 60 aristas y los 30 vértices. Las 20 caras triangulares de la celda de 5 bitruncada se pueden ver eliminadas. El poliedro oblicuo regular dual, {4,6|3}, está relacionado de manera similar con las caras cuadradas de la celda de 5 bitruncada .

Disfenoidal de 30 células

Disfenoidal de 30 células
Tipo	policoron perfecto ^[3]
Símbolo	1,2 _A₄^[3 ]
Coxeter
Células	30 difénoides tetragonales congruentes
Caras	60 triángulos isósceles congruentes (2 aristas cortas)
Bordes	40	20 de longitud 20 de longitud $\scriptstyle 1$ $\scriptstyle {\sqrt {3/5}}$
Vértices	10
Figura de vértice	( Triakis tetraedro )
Dual	Bittruncadas de 5 celdas
Grupo Coxeter	Aut (A ₄ ), [[3,3,3]], orden 240
Vector de órbita	(1, 2, 1, 1)
Propiedades	convexo , isocórico

El difenoide de 30 celdas es el dual del bitruncado de 5 celdas. Es un politopo de 4 dimensiones (o policoron ) derivado del de 5 celdas . Es la envoltura convexa de dos de 5 celdas en orientaciones opuestas.

Al ser el dual de un policoron uniforme, es transitivo a nivel celular y está formado por 30 difenoides tetragonales congruentes . Además, es transitivo a nivel de vértice bajo el grupo Aut(A ₄ ).

Politopos relacionados

Estos politopos pertenecen a un conjunto de 9 4-politopos uniformes construidos a partir del grupo de Coxeter [3,3,3] .

Nombre	5 celdas	5 celdas truncadas	5 celdas rectificadas	cantelado de 5 celdas	bitruncado de 5 celdas	cantitruncado de 5 celdas	Runcinated de 5 celdas	Runcitruncado de 5 celdas	omnitruncado de 5 celdas
Símbolo de Schläfli	{3,3,3} 3r{3,3,3}	t{3,3,3} 2t{3,3,3}	r{3,3,3} 2r{3,3,3}	rr{3,3,3} r2r{3,3,3}	2t{3,3,3}	tr{3,3,3} t2r{3,3,3}	t0,3 { _3,3,3 }	t0,1,3 {3,3,3} _t0,2,3 { _3,3,3 }	t0,1,2,3 { _3,3,3 }
Diagrama de Coxeter
Diagrama de Schlegel
Gráfico de ₄ planos de Coxeter
Gráfico de ₃ planos de Coxeter
Gráfico de ₂ planos de Coxeter

Referencias

HSM Coxeter :
- HSM Coxeter, Politopos regulares , 3.ª edición, Dover, Nueva York, 1973
- Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
  - (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
Coxeter , La belleza de la geometría: doce ensayos , Dover Publications, 1999, ISBN 0-486-40919-8 pág. 88 (Capítulo 5: Poliedros regulares sesgados en tres y cuatro dimensiones y sus análogos topológicos, Actas de la London Mathematics Society, Ser. 2, Vol 43, 1937.)
- Coxeter, HSM Poliedros oblicuos regulares en tres y cuatro dimensiones. Proc. London Math. Soc. 43, 33-62, 1937.
Manuscrito de politopos uniformes de Norman Johnson (1991)
- NW Johnson: La teoría de los politopos uniformes y los panales de abejas , Ph.D. (1966)
1. Polícora uniforme convexa basada en el pentacorono - Modelo 3, George Olshevsky.
Klitzing, Richard. "Polítopos uniformes 4D (policora)".x3x3o3o - propina, o3x3x3o - deca

Específico

^ Klitzing, Richard. "x3x4o3o - punta".
^ Klitzing, Richard. "x3o4x3o - desgarro".
^ ab Sobre 4-politopos perfectos Gabor Gévay Contribuciones al álgebra y la geometría Volumen 43 (2002), No. 1, 243-259 ] Tabla 2, página 252

en a mi Politopos fundamentales convexos regulares y uniformes en dimensiones 2–10
Familia	Un	Bn	Yo ₂ (p) / D _n	Mi ₆ / Mi ₇ / Mi ₈ / Fa ₄ / Sol ₂	H- _n
Polígono regular	Triángulo	Cuadrado	p-gon	Hexágono	Pentágono
Poliedro uniforme	Tetraedro	Octaedro • Cubo	Semicubo		Dodecaedro • Icosaedro
Policoron uniforme	Pentachoron	16 celdas • Tesseract	Acto de Demitesseract	24 celdas	120 celdas • 600 celdas
Politopo 5 uniforme	5-símplex	5-ortoplex • 5-cubo	5-demicubes
Politopo uniforme de 6 elementos	6-símplex	6-ortoplex • 6-cubo	6-demicubes	1 ₂₂ • 2 ₂₁
Politopo 7 uniforme	7-símplex	7-ortoplex • 7-cubo	7-demicube	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Politopo 8 uniforme	8-símplex	8-ortoplex • 8-cubo	8-demicubes	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Politopo uniforme de 9 elementos	9-símplex	9-ortoplex • 9-cubo	9-demicubes
Politopo uniforme de 10	10-símplex	10-ortoplex • 10-cubo	10-demicubes
Politopo uniforme n	n - símplex	n - ortoplex • n - cubo	n - demicubo	1 _k2 • 2 _k1 • k21	n - politopo pentagonal
Temas: Familias de politopos • Politopo regular • Lista de politopos regulares y compuestos

[1] Klitzing, Richard. "x3x4o3o - punta".

[2] Klitzing, Richard. "x3o4x3o - desgarro".

[Gevay-3] Sobre 4-politopos perfectos Gabor Gévay Contribuciones al álgebra y la geometría Volumen 43 (2002), No. 1, 243-259 ] Tabla 2, página 252