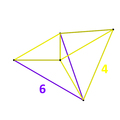
Runcinado de 5 células

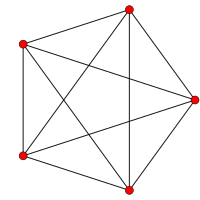5 celdas	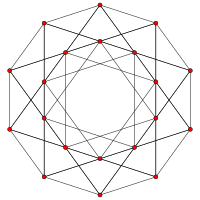Runcinado de 5 células
Runcitruncado de 5 celdas	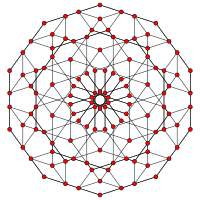Omnitruncado de 5 células (runcicantitruncado de 5 células)
Proyecciones ortogonales en el plano A 4 de Coxeter

En geometría de cuatro dimensiones , una 5-celda runcinada es un 4-politopo uniforme convexo , que es una runcinación (un truncamiento de tercer orden, hasta el planeamiento de las caras ) de la 5-celda regular .

Hay 3 grados únicos de runcinaciones de las 5 celdas, incluidas permutaciones, truncamientos y cantelaciones.

Runcinado de 5 células
Diagrama de Schlegel con la mitad de las celdas tetraédricas visibles.
Tipo	Politopo 4 uniforme
Símbolo de Schläfli	t0,3 { 3,3,3 }
Diagrama de Coxeter
Células	30	10 ( 3.3.3 ) 20 ( 3.4.4 )
Caras	70	40 {3} 30 {4}
Bordes	60
Vértices	20
Figura de vértice	(Antiprisma triangular equilátero alargado)
Grupo de simetría	Aut (A 4 ), [[3,3,3]], orden 240
Propiedades	convexo , isogonal , isotoxal
Índice uniforme	4 5 6

El prismatodecacoron runcinado de 5 celdas o pequeño prismatodecacoron se construye expandiendo radialmente las celdas de un 5-cell y rellenando los huecos con prismas triangulares (que son los prismas de las caras y las figuras de las aristas) y tetraedros (celdas del 5-cell dual). Está formado por 10 tetraedros y 20 prismas triangulares. Los 10 tetraedros corresponden a las celdas de un 5-cell y su dual.

Topológicamente, bajo su máxima simetría, [[3,3,3]], sólo hay una forma geométrica, que contiene 10 tetraedros y 20 prismas triangulares uniformes. Los rectángulos son siempre cuadrados porque los dos pares de aristas corresponden a las aristas de los dos conjuntos de 5 tetraedros regulares cada uno en orientación dual, que se hacen iguales bajo simetría extendida.

EL Elte lo identificó en 1912 como un politopo semirregular.

• Runcinated de 5 celdas ( Norman Johnson )
• Pentacoron runcinado
• 4-símplex runcinado
• Pentacoron expandido de 5 celdas/4 símplex
• Prismatodecacoron pequeño (acrónimo: Spid) (Jonathan Bowers)

Dos de las diez celdas tetraédricas se encuentran en cada vértice. Los prismas triangulares se encuentran entre ellas, unidos a ellas por sus caras triangulares y entre sí por sus caras cuadradas. Cada prisma triangular está unido a sus prismas triangulares vecinos en orientación anti (es decir, si las aristas A y B en la cara cuadrada compartida están unidas a las caras triangulares de un prisma, entonces son las otras dos aristas las que están unidas a las caras triangulares del otro prisma); por lo tanto, cada par de prismas adyacentes, si se rota en el mismo hiperplano , formaría un girobifastigio .

Visto en una matriz de configuración , se muestran todos los recuentos de incidencia entre elementos. Los números del vector f diagonal se derivan a través de la construcción de Wythoff , dividiendo el orden de grupo completo de un orden de subgrupo eliminando un espejo a la vez. ^[1]

	por favor	o0​	el 1		el 2			F3​
	o0​	20	3	3	3	6	3	1	3	3	1
	el 1	2	30	*	2	2	0	1	2	1	0
		2	*	30	0	2	2	0	1	2	1
	el 2	3	3	0	20	*	*	1	1	0	0
		4	2	2	*	30	*	0	1	1	0
		3	0	3	*	*	20	0	0	1	1
	F3​	4	6	0	4	0	0	5	*	*	*
		6	6	3	2	3	0	*	10	*	*
		6	3	6	0	3	2	*	*	10	*
		4	0	6	0	0	4	*	*	*	5

El cuboctaedro central de 5 celdas puede ser diseccionado en dos cúpulas tetraédricas . Esta disección es análoga a la del cuboctaedro 3D diseccionado por un hexágono central en dos cúpulas triangulares .

proyecciones ortográficas

Un avión de Coxeter	Un 4	Un 3	Un 2
Gráfico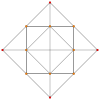
Simetría diedral	[[5]] = [10]	[4]	[[3]] = [6]

Vista del interior de un diagrama de Schlegel de proyección de 3 esferas con sus 10 celdas tetraédricas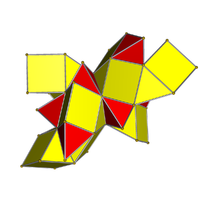

Neto

Las coordenadas cartesianas de los vértices de un triángulo rectángulo de 5 celdas centrado en el origen con una longitud de arista de 2 son:

Se puede crear un conjunto alternativo más simple de coordenadas en el espacio 5, como 20 permutaciones de:

(0,1,1,1,2)

Esta construcción existe como una de las 32 facetas ortantes del 5-ortoplex runcinado .

Una segunda construcción en el espacio 5, desde el centro de un ortoplex 5 rectificado, se da mediante permutaciones de coordenadas de:

(1,-1,0,0,0)

Sus 20 vértices representan los vectores raíz del grupo de Lie simple A ₄ . También es la figura de vértice para el panal de 5 celdas en el espacio 4.

La sección transversal máxima de la celda de 5 cuerpos runcinados con un hiperplano tridimensional es un cuboctaedro . Esta sección transversal divide la celda de 5 cuerpos runcinados en dos hipercúpulas tetraédricas que constan de 5 tetraedros y 10 prismas triangulares cada una.

La proyección ortográfica tetraédrica de la quinta celda runcinada en el espacio tridimensional tiene una envoltura cuboctaédrica . La estructura de esta proyección es la siguiente:

• La envoltura cuboctaédrica se divide internamente de la siguiente manera:

• Cuatro tetraedros aplanados unen 4 de las caras triangulares del cuboctaedro a un tetraedro central. Estas son las imágenes de 5 de las celdas tetraédricas.
• Las 6 caras cuadradas del cuboctaedro están unidas a las aristas del tetraedro central mediante prismas triangulares deformados. Éstas son las imágenes de 6 de las celdas del prisma triangular.
• Las otras 4 caras triangulares están unidas al tetraedro central mediante 4 prismas triangulares (distorsionados por proyección). Éstas son las imágenes de otras 4 celdas del prisma triangular.
• Esto representa la mitad del sistema runcinado de cinco celdas (cinco tetraedros y diez prismas triangulares), que puede considerarse como el «hemisferio norte».

• La otra mitad, el 'hemisferio sur', corresponde a una división isomorfa del cuboctaedro en orientación dual, en la que el tetraedro central es dual al de la primera mitad. Las caras triangulares del cuboctaedro unen los prismas triangulares de un hemisferio con los tetraedros aplanados del otro hemisferio, y viceversa. Así, el hemisferio sur contiene otros 5 tetraedros y otros 10 prismas triangulares, lo que hace un total de 10 tetraedros y 20 prismas triangulares.

El poliedro oblicuo regular {4,6|3} existe en el espacio 4 con 6 cuadrados alrededor de cada vértice, en una figura de vértice no plana en zigzag. Estas caras cuadradas se pueden ver en la celda de 5 celdas ahusadas, utilizando las 60 aristas y los 20 vértices. Las 40 caras triangulares de la celda de 5 celdas ahusadas se pueden ver eliminadas. El poliedro oblicuo regular dual {6,4|3} está relacionado de manera similar con las caras hexagonales de la celda de 5 celdas ahusadas .

Runcitruncado de 5 celdas
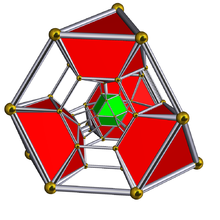Diagrama de Schlegel con células cuboctaédricas mostradas
Tipo	Politopo 4 uniforme
Símbolo de Schläfli	t0,1,3 { 3,3,3}
Diagrama de Coxeter
Células	30	5(3.6.6) 10(4.4.6) 10(3.4.4) 5(3.4.3.4)
Caras	120	40 {3} 60 {4} 20 {6}
Bordes	150
Vértices	60
Figura de vértice	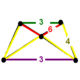(Pirámide rectangular)
Grupo Coxeter	A 4 , [3,3,3], orden 120
Propiedades	convexo , isogonal
Índice uniforme	7 8 9

El pentacorone prismatorombado o runcitruncado de cinco celdas está compuesto por 60 vértices, 150 aristas, 120 caras y 30 celdas. Las celdas son: 5 tetraedros truncados , 10 prismas hexagonales , 10 prismas triangulares y 5 cuboctaedros . Cada vértice está rodeado por cinco celdas: un tetraedro truncado, dos prismas hexagonales, un prisma triangular y un cuboctaedro; la figura del vértice es una pirámide rectangular.

• Pentacorone runcitruncado
• 4-símplex runcitruncado
• Diprismatodispentachoron
• Pentacoron prismatorombated (acrónimo: prip) (Jonathan Bowers)

Visto en una matriz de configuración , se muestran todos los recuentos de incidencia entre elementos. Los números del vector f diagonal se derivan a través de la construcción de Wythoff , dividiendo el orden de grupo completo de un orden de subgrupo eliminando un espejo a la vez. ^[2]

	por favor	o0​	el 1			el 2					F3​
	o0​	60	1	2	2	2	2	1	2	1	1	2	1	1
	el 1	2	30	*	*	2	2	0	0	0	1	2	1	0
		2	*	60	*	1	0	1	1	0	1	1	0	1
		2	*	*	60	0	1	0	1	1	0	1	1	1
	el 2	6	3	3	0	20	*	*	*	*	1	1	0	0
		4	2	0	2	*	30	*	*	*	0	1	1	0
		3	0	3	0	*	*	20	*	*	1	0	0	1
		4	0	2	2	*	*	*	30	*	0	1	0	1
		3	0	0	3	*	*	*	*	20	0	0	1	1
	F3​	12	6	12	0	4	0	4	0	0	5	*	*	*
		12	6	6	6	2	3	0	3	0	*	10	*	*
		6	3	0	6	0	3	0	0	2	*	*	10	*
		12	0	12	12	0	0	4	6	4	*	*	*	5

proyecciones ortográficas

Un avión de Coxeter	Un 4	Un 3	Un 2
Gráfico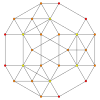
Simetría diedral	[5]	[4]	[3]

Diagrama de Schlegel con sus 40 caras triangulares azules y sus 60 caras cuadrangulares verdes.

Parte central del diagrama de Schlegel.

Las coordenadas cartesianas de un sistema de 5 celdas truncadas y centrado en el origen que tiene una longitud de arista de 2 son:

Los vértices se pueden construir de forma más sencilla en un hiperplano en el espacio de 5, como las permutaciones de:

(0,1,1,2,3)

Esta construcción proviene de la faceta ortante positiva del 5-ortoplex runcitruncado .

Omnitruncado de 5 celdas
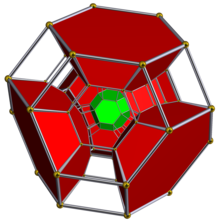Diagrama de Schlegel con la mitad de las celdas octaédricas truncadas mostradas.
Tipo	Politopo 4 uniforme
Símbolo de Schläfli	t0,1,2,3 { 3,3,3 }
Diagrama de Coxeter
Células	30	10(4.6.6) 20(4.4.6)
Caras	150	90{4} 60{6}
Bordes	240
Vértices	120
Figura de vértice	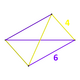Disfenoide fílico
Grupo Coxeter	Aut (A 4 ), [[3,3,3]], orden 240
Propiedades	convexo , isogonal , zonotopo
Índice uniforme	8 9 10

El prismatodecacoron omnitruncado de 5 celdas o gran prismatodecacoron está compuesto por 120 vértices, 240 aristas, 150 caras (90 cuadrados y 60 hexágonos ) y 30 celdas. Las celdas son: 10 octaedros truncados y 20 prismas hexagonales . Cada vértice está rodeado por cuatro celdas: dos octaedros truncados y dos prismas hexagonales, dispuestos en dos figuras de vértice diesfenoidales fílicas .

Coxeter llama a esto el politopo de Hinton en honor a C. H. Hinton , quien lo describió en su libro La cuarta dimensión en 1906. Forma un panal uniforme que Coxeter llama panal de Hinton . ^[3]

• Omnitruncado de 5 celdas
• Pentacoron omnitruncado
• 4-símplex omnitruncado
• Gran prismatodecacoron (acrónimo: gippid) (Jonathan Bowers)
• Politopo de Hinton ( Coxeter )

Visto en una matriz de configuración , se muestran todos los recuentos de incidencia entre elementos. Los números del vector f diagonal se derivan a través de la construcción de Wythoff , dividiendo el orden de grupo completo de un orden de subgrupo eliminando un espejo a la vez. ^[4]

	por favor	o0​	el 1				el 2						F3​
	o0​	120	1	1	1	1	1	1	1	1	1	1	1	1	1	1
	el 1	2	60	*	*	*	1	1	1	0	0	0	1	1	1	0
		2	*	60	*	*	1	0	0	1	1	0	1	1	0	1
		2	*	*	60	*	0	1	0	1	0	1	1	0	1	1
		2	*	*	*	60	0	0	1	0	1	1	0	1	1	1
	el 2	6	3	3	0	0	20	*	*	*	*	*	1	1	0	0
		4	2	0	2	0	*	30	*	*	*	*	1	0	1	0
		4	2	0	0	2	*	*	30	*	*	*	0	1	1	0
		6	0	3	3	0	*	*	*	20	*	*	1	0	0	1
		4	0	2	0	2	*	*	*	*	30	*	0	1	0	1
		6	0	0	3	3	*	*	*	*	*	20	0	0	1	1
	F3​	24	12	12	12	0	4	6	0	4	0	0	5	*	*	*
		12	6	6	0	6	2	0	3	0	3	0	*	10	*	*
		12	6	0	6	6	0	3	3	0	0	2	*	*	10	*
		24	0	12	12	12	0	0	0	4	6	4	*	*	*	5

proyecciones ortográficas

Un avión de Coxeter	Un 4	Un 3	Un 2
Gráfico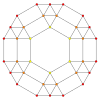
Simetría diedral	[[5]] = [10]	[4]	[[3]] = [6]

Neto

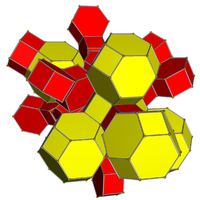Omnitruncado de 5 celdas

Doble a omnitruncado de 5 celdas

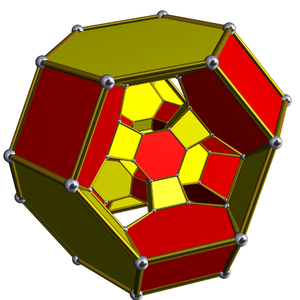Diagrama de Schlegel en perspectiva centrado en el octaedro truncado

Proyección estereográfica

Así como el octaedro truncado es el permutoedro de orden 4, la celda de 5 omnitruncada es el permutoedro de orden 5. ^[5] La celda de 5 omnitruncada es un zonotopo , la suma de Minkowski de cinco segmentos de línea paralelos a las cinco líneas que pasan por el origen y los cinco vértices de la celda de 5.

El panal omnitruncado de 5 celdas puede teselar el espacio de 4 dimensiones mediante copias traslacionales de esta celda, cada una con 3 hiperceldas alrededor de cada cara. El diagrama de Coxeter de este panal es. ^[6] A diferencia del panal análogo en tres dimensiones, el panal cúbico bitruncado que tiene tres construcciones Wythoff de grupo Coxeter diferentes , este panal tiene solo una de esas construcciones. ^[3]

La celda 5 omnitruncada tiene simetría pentacórica extendida, [[3,3,3]], orden 240. La figura del vértice de la celda 5 omnitruncada representa el tetraedro de Goursat del grupo de Coxeter [3,3,3] . La simetría extendida proviene de una rotación doble a través de la rama de orden 3 media, y se representa de manera más explícita como [2 ⁺ [3,3,3]].

Las coordenadas cartesianas de los vértices de un sistema omnitruncado de 5 celdas centrado en el origen que tiene una longitud de arista de 2 son:

Estos vértices se pueden obtener de forma más sencilla en el espacio 5 como las 120 permutaciones de (0,1,2,3,4). Esta construcción se basa en la faceta ortante positiva del 5-ortoplex runcicantitruncado , t _0,1,2,3 {3,3,3,4},.

Las variantes no uniformes con simetría [3,3,3] y dos tipos de octaedros truncados se pueden duplicar colocando los dos tipos de octaedros truncados uno sobre el otro para producir un policoronte no uniforme con 10 octaedros truncados , dos tipos de 40 prismas hexagonales (20 prismas ditrigonales y 20 trapezoprismas ditrigonales), dos tipos de 90 trapezoprismas rectangulares (30 con simetría D _2d y 60 con simetría C _2v ) y 240 vértices. Su figura de vértice es una bipirámide triangular irregular .

Figura de vértice

Este policoron puede entonces alternarse para producir otro policoron no uniforme con 10 icosaedros , dos tipos de 40 octaedros (20 con simetría S ₆ y 20 con simetría D ₃ ), tres tipos de 210 tetraedros (30 difenoides tetragonales, 60 difenoides fílicos y 120 tetraedros irregulares) y 120 vértices. Tiene una simetría de [[3,3,3] ⁺ ], orden 120.

Figura de vértice

El snub completo de 5 celdas o el omnisnub de 5 celdas , definido como una alternancia del snub omnitruncado de 5 celdas, no se puede hacer uniforme, pero se puede dar un diagrama de Coxeter., y simetría [[3,3,3]] ⁺ , orden 120, y construido a partir de 90 celdas: 10 icosaedros , 20 octaedros y 60 tetraedros que llenan los huecos en los vértices eliminados. Tiene 300 caras (triángulos), 270 aristas y 60 vértices.

Topológicamente, bajo su simetría más alta, [[3,3,3]] ⁺ , los 10 icosaedros tienen simetría T (tetraédrica quiral), mientras que los 20 octaedros tienen simetría D ₃ y los 60 tetraedros tienen simetría C ₂ . ^[7]

Estos politopos son parte de una familia de 9 politopos uniformes 4 construidos a partir del grupo de Coxeter [3,3,3] .

Nombre	5 celdas	5 celdas truncadas	5 celdas rectificadas	cantelado de 5 celdas	bitruncado de 5 celdas	cantitruncado de 5 celdas	Runcinated de 5 celdas	Runcitruncado de 5 celdas	omnitruncado de 5 celdas
Símbolo de Schläfli	{3,3,3} 3r{3,3,3}	t{3,3,3} 2t{3,3,3}	r{3,3,3} 2r{3,3,3}	rr{3,3,3} r2r{3,3,3}	2t{3,3,3}	tr{3,3,3} t2r{3,3,3}	t0,3 { 3,3,3 }	t0,1,3 {3,3,3} t0,2,3 { 3,3,3 }	t0,1,2,3 { 3,3,3 }
Diagrama de Coxeter
Diagrama de Schlegel
Gráfico de 4 planos de Coxeter
Gráfico de 3 planos de Coxeter
Gráfico de 2 planos de Coxeter

• HSM Coxeter :
  • HSM Coxeter, Politopos regulares , 3.ª edición, Dover, Nueva York, 1973
  • Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
    • (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
    • (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
• Manuscrito de politopos uniformes de Norman Johnson (1991)
  • NW Johnson: La teoría de politopos uniformes y panales , Ph.D.
• 1. Polícora uniforme convexa basada en el pentacorono – Modelos 5, 8 y 9, George Olshevsky.
• Klitzing, Richard. "Polítopos uniformes 4D (policora)".o3x3x3o - spid, x3x3o3x - prip, x3x3x3x - gippid