6-ortoplex
Hexacross de 6 ortoplex | |
|---|---|
 Proyección ortogonal dentro del polígono de Petrie | |
| Tipo | Politopo 6 regular |
| Familia | ortoplex |
| Símbolos de Schläfli | {3,3,3,3,4} {3,3,3,3 1,1 } |
| Diagramas de Coxeter-Dynkin |                     = =     |
| 5 caras | 64 {3 4 } |
| 4 caras | 192 {3 3 } |
| Células | 240 {3,3} |
| Caras | 160 {3} |
| Bordes | 60 |
| Vértices | 12 |
| Figura de vértice | 5-ortoplex |
| Polígono de Petrie | dodecágono |
| Grupos de Coxeter | B 6 , [4,3 4 ] D 6 , [3 3,1,1 ] |
| Dual | 6 cubos |
| Propiedades | convexo , politopo de Hanner |
En geometría , un 6-ortoplex , o politopo de 6 cruces , es un 6-politopo regular con 12 vértices , 60 aristas , 160 caras triangulares , 240 celdas de tetraedro , 192 5 celdas de 4 caras y 64 5 caras .
Tiene dos formas construidas, la primera regular con el símbolo de Schläfli {3 4 ,4}, y la segunda con facetas etiquetadas alternativamente (en tablero de ajedrez), con el símbolo de Schläfli {3,3,3,3 1,1 } o el símbolo de Coxeter 3 11 .
Forma parte de una familia infinita de politopos, llamados politopos cruzados u ortoplexos . El politopo dual es el hipercubo de 6 , o hexeracto .
Nombres alternativos
- Hexacross , derivado de la combinación del nombre de familia cross polytope con hex para seis (dimensiones) en griego .
- Hexacontitetrapeton como un 6-politopo de 64 facetas .
Como configuración
Esta matriz de configuración representa el 6-ortoplex. Las filas y columnas corresponden a vértices, aristas, caras, celdas, 4-caras y 5-caras. Los números diagonales indican cuántos elementos de cada uno se encuentran en todo el 6-ortoplex. Los números no diagonales indican cuántos elementos de la columna se encuentran en el elemento de la fila o en él. [1] [2]
Construcción
Hay tres grupos de Coxeter asociados con el 6-ortoplex, uno regular , dual del hexeracto con el grupo de Coxeter C 6 o [4,3,3,3,3] , y una semisimetría con dos copias de facetas 5-símplex, alternadas, con el grupo de Coxeter D 6 o [3 3,1,1 ]. Una construcción de simetría mínima se basa en un dual de un 6- ortotopo , llamado 6-fusil .
| Nombre | Coxeter | Colapso | Simetría | Orden |
|---|---|---|---|---|
| Ortoplex 6 regular |            | {3,3,3,3,4} | [4,3,3,3,3] | 46080 |
| Ortoplex 6 cuasirregular |          | {3,3,3,3 1,1 } | [3,3,3,3 1,1 ] | 23040 |
| 6 fusiles |            | {3,3,3,4}+{} | [4,3,3,3,3] | 7680 |
           | {3,3,4}+{4} | [4,3,3,2,4] | 3072 | |
           | 2{3,4} | [4,3,2,4,3] | 2304 | |
           | {3,3,4}+2{} | [4,3,3,2,2] | 1536 | |
           | {3,4}+{4}+{} | [4,3,2,4,2] | 768 | |
           | 3{4} | [4,2,4,2,4] | 512 | |
           | {3,4}+3{} | [4,3,2,2,2] | 384 | |
           | 2{4}+2{} | [4,2,4,2,2] | 256 | |
           | {4}+4{} | [4,2,2,2,2] | 128 | |
           | 6{} | [2,2,2,2,2] | 64 |
Coordenadas cartesianas
Las coordenadas cartesianas para los vértices de un 6-ortoplex, centrado en el origen son
- (±1,0,0,0,0,0), (0,±1,0,0,0,0), (0,0,±1,0,0,0), (0,0, 0,±1,0,0), (0,0,0,0,±1,0), (0,0,0,0,0,±1)
Cada par de vértices está conectado por una arista , excepto los opuestos.
Imágenes
| Avión Coxeter | B6 | B 5 | B4 |
|---|---|---|---|
| Gráfico |  |  |  |
| Simetría diedral | [12] | [10] | [8] |
| Avión Coxeter | B3 | B2 | |
| Gráfico |  |  | |
| Simetría diedral | [6] | [4] | |
| Avión Coxeter | Un 5 | Un 3 | |
| Gráfico | 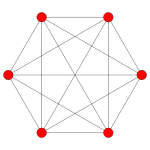 |  | |
| Simetría diedral | [6] | [4] |
Politopos relacionados
El 6-ortoplex se puede proyectar en 3 dimensiones en los vértices de un icosaedro regular . [3]
| 2D | 3D | ||
|---|---|---|---|
 Icosaedro {3,5} =      Avión H 3 Coxeter | 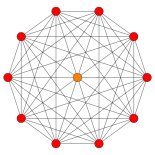 6-ortoplex {3,3,3,3 1,1 } =          Avión D 6 Coxeter |  Icosaedro |  6-ortoplex |
Esta construcción puede verse geométricamente como los 12 vértices del 6-ortoplex proyectados a 3 dimensiones como los vértices de un icosaedro regular . Esto representa un plegado geométrico de los grupos de Coxeter de D 6 a H 3 : :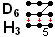      a a     A la izquierda, vistos mediante estas proyecciones ortogonales del plano de Coxeter 2D , los dos vértices centrales superpuestos definen el tercer eje en esta proyección. Todos los pares de vértices del 6-ortoplex están conectados, excepto los opuestos: 30 aristas se comparten con el icosaedro, mientras que 30 aristas más del 6-ortoplex se proyectan hacia el interior del icosaedro. A la izquierda, vistos mediante estas proyecciones ortogonales del plano de Coxeter 2D , los dos vértices centrales superpuestos definen el tercer eje en esta proyección. Todos los pares de vértices del 6-ortoplex están conectados, excepto los opuestos: 30 aristas se comparten con el icosaedro, mientras que 30 aristas más del 6-ortoplex se proyectan hacia el interior del icosaedro. | |||
Se trata de una serie dimensional de politopos y panales uniformes, expresada por Coxeter como una serie 3 k1 . (Existe un caso degenerado de 4 dimensiones como teselación de 3 esferas, un hosoedro tetraédrico ).
| Espacio | Finito | Euclidiano | Hiperbólico | |||
|---|---|---|---|---|---|---|
| norte | 4 | 5 | 6 | 7 | 8 | 9 |
Grupo Coxeter | Un 3 Un 1 | Un 5 | D6 | E7 | =E 7 + | = E7 ++ |
Diagrama de Coxeter |        |        |          |            |              |                |
| Simetría | [3 −1,3,1 ] | [3 0,3,1 ] | [[3 1,3,1 ]] = [4,3,3,3,3] | [3 2,3,1 ] | [3 3,3,1 ] | [3 4,3,1 ] |
| Orden | 48 | 720 | 46.080 | 2.903.040 | ∞ | |
| Gráfico |  |  |  | - | - | |
| Nombre | 3 1,-1 | 3 10 | 311 | 3 21 | 3 31 | 341 |
Este politopo es uno de los 63 politopos 6 uniformes generados a partir del plano de Coxeter B 6 , incluido el 6-cubo o 6-ortoplex regular.
Referencias
- HSM Coxeter :
- HSM Coxeter, Politopos regulares , 3.ª edición, Dover, Nueva York, 1973
- Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
- (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
- Manuscrito de politopos uniformes de Norman Johnson (1991)
- NW Johnson: La teoría de los politopos uniformes y los panales de abejas , Ph.D. 1966
- Klitzing, Richard. "Polipetas (politopos) uniformes 6D x3o3o3o3o4o - gee".
- Específico
- ^ Coxeter, Politopos regulares, sección 1.8 Configuraciones
- ^ Coxeter, Politopos regulares complejos, p.117
- ^ Cuasicristales y geometría , Marjorie Senechal, 1996, Cambridge University Press, pág. 64. 2.7.1 El cristal I 6
Enlaces externos
- Olshevsky, George. «Politopo cruzado». Glosario de hiperespacio . Archivado desde el original el 4 de febrero de 2007.
- Politopos de varias dimensiones
- Glosario multidimensional

































































