Número cuántico

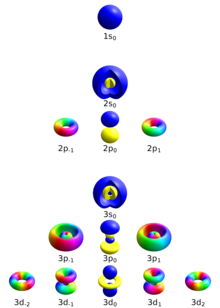
Parte de una serie de artículos sobre
Mecánica cuántica
${\displaystyle i\hbar {\frac {d}{dt}}|\Psi \rangle ={\hat {H}}|\Psi \rangle }$ Ecuación de Schrödinger
Introducción Glosario Historia
Fondo Mecánica clásica Antigua teoría cuántica Notación de corchetes Hamiltoniano Interferencia
Fundamentos Complementariedad Decoherencia Enredo Nivel de energía Medición No localidad Número cuántico Estado Superposición Simetría Túnel Incertidumbre Función de onda Colapsar
Experimentos Desigualdad de Bell Desigualdad de CHSH Davisson-Germer Doble rendija Elitzur–Vaidman Franck-Hertz Desigualdad de Leggett Desigualdad de Leggett-Garg Mach–Zehnder Corchete Borrador cuántico Elección retrasada El gato de Schrödinger Stern–Gerlach La elección retrasada de Wheeler
Formulaciones Descripción general Heisenberg Interacción Matriz Espacio de fases Schrödinger Suma de historias (integral de trayectoria)
Ecuaciones Dirac Klein-Gordon Pablo Rydberg Schrödinger
Interpretaciones Bayesiano Historias consistentes Copenhague de Broglie–Bohm Conjunto Variable oculta Local Superdeterminismo Muchos mundos Colapso objetivo Lógica cuántica Relacional Transaccional De von Neumann-Wigner
Temas avanzados Mecánica cuántica relativista Teoría cuántica de campos Quantum information science Quantum computing Quantum chaos EPR paradox Density matrix Scattering theory Quantum statistical mechanics Quantum machine learning
Scientists Aharonov Bell Bethe Blackett Bloch Bohm Bohr Born Bose de Broglie Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordan Kramers Lamb Landau Laue Moseley Millikan Onnes Pauli Planck Rabi Raman Rydberg Schrödinger Simmons Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

En física y química cuántica , los números cuánticos son magnitudes que caracterizan los posibles estados del sistema. Para especificar completamente el estado del electrón en un átomo de hidrógeno, se necesitan cuatro números cuánticos. El conjunto tradicional de números cuánticos incluye los números cuánticos principal , azimutal , magnético y de espín . Para describir otros sistemas, se requieren números cuánticos diferentes. Para las partículas subatómicas, es necesario introducir nuevos números cuánticos, como el sabor de los quarks , que no tienen correspondencia clásica.

Los números cuánticos están estrechamente relacionados con los valores propios de los observables . Cuando el observable correspondiente conmuta con el hamiltoniano del sistema, se dice que el número cuántico es " bueno " y actúa como una constante de movimiento en la dinámica cuántica.

En la era de la antigua teoría cuántica , a partir de la propuesta de Max Planck de cuantos en su modelo de radiación de cuerpo negro (1900) y la adaptación del concepto de Albert Einstein para explicar el efecto fotoeléctrico (1905), y hasta que Erwin Schrödinger publicó su ecuación de función propia en 1926, ^[1] el concepto detrás de los números cuánticos desarrollados con base en la espectroscopia atómica y teorías de la mecánica clásica con restricciones ad hoc adicionales. ^{[2] : 106} Muchos resultados de la espectroscopia atómica se habían resumido en la fórmula de Rydberg que involucra diferencias entre dos series de energías relacionadas por pasos enteros. El modelo del átomo , propuesto por primera vez por Niels Bohr en 1913, se basó en un solo número cuántico. Junto con la restricción de Bohr de que la absorción de radiación no es clásica, fue capaz de explicar la porción de la serie de Balmer de la fórmula del espectro atómico de Rydberg. ^[3]

Como Bohr señala en su posterior conferencia Nobel, el siguiente paso lo dio Arnold Sommerfeld en 1915. ^[4] El modelo atómico de Sommerfeld añadió un segundo número cuántico y el concepto de integrales de fase cuantificadas para justificarlos. ^{[5] : 207} El modelo de Sommerfeld todavía era esencialmente bidimensional, modelando al electrón como orbitando en un plano; en 1919 extendió su trabajo a tres dimensiones utilizando la "cuantización espacial" en lugar de las integrales de fase cuantificadas. ^{[6] : 152} Karl Schwarzschild y el estudiante de Sommerfeld, Paul Epstein , demostraron independientemente que agregar un tercer número cuántico daba una explicación completa de los resultados del efecto Stark .

Una consecuencia de la cuantificación espacial fue que la interacción orbital del electrón con un campo magnético externo se cuantizó. Esto pareció confirmarse cuando los resultados del experimento de Stern-Gerlach informaron resultados cuantizados para átomos de plata en un campo magnético no homogéneo. La confirmación resultó ser prematura: se necesitarían más números cuánticos. ^[7]

El cuarto y quinto número cuántico de la era atómica surgieron de los intentos de comprender el efecto Zeeman . Al igual que el experimento de Stern-Gerlach, el efecto Zeeman refleja la interacción de los átomos con un campo magnético; en un campo débil, los resultados experimentales se denominaron "anómalos" y divergían de cualquier teoría de la época. La solución de Wolfgang Pauli a este problema fue introducir otro número cuántico que solo tomaba dos valores posibles, . ^[8] Esto finalmente se convertiría en los valores cuantizados de la proyección de espín , un cuanto de momento angular intrínseco del electrón. En 1927, Ronald Fraser demostró que la cuantización en el experimento de Stern-Gerlach se debía al momento magnético asociado con el espín del electrón en lugar de su momento angular orbital. ^[7] El éxito de Pauli en el desarrollo de los argumentos para un número cuántico de espín sin depender de los modelos clásicos preparó el terreno para el desarrollo de números cuánticos para partículas elementales en el resto del siglo XX. ^[8]${\displaystyle \pm \hbar /2}$

Bohr, con su principio de Aufbau o "construcción", y Pauli, con su principio de exclusión, conectaron los números cuánticos electrónicos del átomo en un marco para predecir las propiedades de los átomos. ^[9] Cuando Schrödinger publicó su ecuación de onda y calculó los niveles de energía del hidrógeno, estos dos principios pasaron a convertirse en la base de la física atómica.

Con el éxito de los modelos del átomo, la atención de la física se dirigió a los modelos del núcleo. A partir del modelo inicial de Heisenberg sobre la unión entre protones y neutrones en 1932, Eugene Wigner introdujo el isospín en 1937, el primer número cuántico "interno" no relacionado con una simetría en el espacio-tiempo real. ^{[10] : 45}

A medida que se desarrolló la mecánica cuántica, la abstracción aumentó y los modelos basados ​​en la simetría y la invariancia desempeñaron papeles cada vez más importantes. Dos años antes de su trabajo sobre la ecuación de onda cuántica, Schrödinger aplicó las ideas de simetría originadas por Emmy Noether y Hermann Weyl al campo electromagnético. ^{[11] : 198} A medida que la electrodinámica cuántica se desarrolló en los años 1930 y 1940, la teoría de grupos se convirtió en una herramienta importante. En 1953, Chen Ning Yang se había obsesionado con la idea de que la teoría de grupos podía aplicarse para conectar los números cuánticos conservados de las colisiones nucleares con las simetrías en una teoría de campo de los nucleones. ^{[11] : 202} Con Robert Mills , Yang desarrolló una teoría de calibre no abeliana basada en la conservación de los números cuánticos del isospín nuclear .

Los buenos números cuánticos corresponden a valores propios de operadores que conmutan con el hamiltoniano , cantidades que pueden conocerse con precisión al mismo tiempo que la energía del sistema. Específicamente, los observables que conmutan con el hamiltoniano son diagonalizables simultáneamente con él y, por lo tanto, los valores propios y la energía (valores propios del hamiltoniano) no están limitados por una relación de incertidumbre que surge de la no conmutatividad. En conjunto, una especificación de todos los números cuánticos de un sistema cuántico caracteriza completamente un estado base del sistema y, en principio, se pueden medir juntos. Muchos observables tienen espectros discretos (conjuntos de valores propios) en mecánica cuántica, por lo que las cantidades solo se pueden medir en valores discretos. En particular, esto conduce a números cuánticos que toman valores en conjuntos discretos de números enteros o semienteros ; aunque podrían acercarse al infinito en algunos casos.${\displaystyle a}$

El recuento de números cuánticos varía de un sistema a otro y no tiene una respuesta universal. Por lo tanto, estos parámetros deben encontrarse para cada sistema que se va a analizar. Un sistema cuantizado requiere al menos un número cuántico. La dinámica (es decir, la evolución temporal) de cualquier sistema cuántico se describe mediante un operador cuántico en forma de un hamiltoniano , H. Hay un número cuántico del sistema que corresponde a la energía del sistema; es decir, uno de los valores propios del hamiltoniano. También hay un número cuántico para cada operador linealmente independiente O que conmuta con el hamiltoniano. Un conjunto completo de observables conmutativos (CSCO) que conmutan con el hamiltoniano caracteriza al sistema con todos sus números cuánticos. Existe una relación uno a uno entre los números cuánticos y los operadores del CSCO, y cada número cuántico toma uno de los valores propios de su operador correspondiente. Como resultado de las diferentes bases que pueden elegirse arbitrariamente para formar un conjunto completo de operadores conmutativos, se pueden utilizar diferentes conjuntos de números cuánticos para la descripción del mismo sistema en diferentes situaciones.

Cuatro números cuánticos pueden describir completamente el nivel de energía de un electrón en un átomo similar al hidrógeno :

• Número cuántico principal ( n )
• Número cuántico azimutal ( ℓ )
• Número cuántico magnético ( mℓ ₎
• Número cuántico de espín ( ms ₎

Estos números cuánticos también se utilizan en la descripción clásica de los estados de las partículas nucleares (por ejemplo, protones y neutrones). ^{[ cita requerida ]} Una descripción cuántica de los orbitales moleculares requiere otros números cuánticos, porque las simetrías del sistema molecular son diferentes.

El número cuántico principal describe la capa electrónica de un electrón. El valor de n varía desde 1 hasta la capa que contiene el electrón más externo de ese átomo, es decir ^[12]

n = 1, 2, ...

Por ejemplo, en el cesio (Cs), el electrón de valencia más externo está en la capa con nivel de energía 6, por lo que un electrón en el cesio puede tener un valor n de 1 a 6. La distancia promedio entre el electrón y el núcleo aumenta con n .

El número cuántico azimutal , también conocido como número cuántico del momento angular orbital , describe la subcapa y da la magnitud del momento angular orbital a través de la relación

L ² = ħ ² ℓ ( ℓ + 1).

En química y espectroscopia, ℓ = 0 se denomina orbital s, ℓ = 1 , orbital p, ℓ = 2 , orbital d, y ℓ = 3 , orbital f.

El valor de ℓ varía de 0 a n − 1 , por lo que el primer orbital p ( ℓ = 1 ) aparece en la segunda capa electrónica ( n = 2 ), el primer orbital d ( ℓ = 2 ) aparece en la tercera capa ( n = 3 ), y así sucesivamente: ^[13]

ℓ = 0, 1, 2,..., n − 1

Un número cuántico que comienza en n = 3, ℓ = 0, describe un electrón en el orbital s de la tercera capa electrónica de un átomo. En química, este número cuántico es muy importante, ya que especifica la forma de un orbital atómico e influye fuertemente en los enlaces químicos y los ángulos de enlace . El número cuántico azimutal también puede indicar el número de nodos angulares presentes en un orbital. Por ejemplo, para los orbitales p, ℓ = 1 y, por lo tanto, la cantidad de nodos angulares en un orbital p es 1.

El número cuántico magnético describe el orbital específico dentro de la subcapa y produce la proyección del momento angular orbital a lo largo de un eje específico :

L _z = m _ℓ ħ

Los valores de m _ℓ varían de − ℓ a ℓ , con intervalos enteros. ^{[14] [ página necesaria ]}

La subcapa s ( ℓ = 0 ) contiene solo un orbital y, por lo tanto, el mℓ de un electrón en un orbital s siempre será 0. La subcapa p ( ℓ = 1 ) contiene tres orbitales, por lo que el _mℓ de _un electrón en un orbital p será −1, 0 o 1. La subcapa d ( ℓ = 2 ) contiene cinco orbitales, con _valores mℓ de −2, −1, 0, 1 y 2.

El número cuántico magnético de espín describe el momento angular de espín intrínseco del electrón dentro de cada orbital y da la proyección del momento angular de espín S a lo largo del eje especificado:

S _z = m _s ħ .

En general, los valores de m _s varían de − s a s , donde s es el número cuántico de espín, asociado con la magnitud del momento angular de espín intrínseco de la partícula: ^[15]

m _s = − s , − s + 1, − s + 2, ..., s − 2, s − 1, s .

Un estado electrónico tiene número de espín s = ⁠1/2⁠ , en consecuencia m _s será + ⁠1/2⁠ ("girar hacia arriba") o - ⁠1/2⁠ Estados de "espín descendente". Como los electrones son fermiones, obedecen al principio de exclusión de Pauli : cada estado electrónico debe tener números cuánticos diferentes. Por lo tanto, cada orbital estará ocupado por dos electrones como máximo, uno por cada estado de espín.

Un átomo multielectrónico puede modelarse cualitativamente como un átomo similar al hidrógeno con una carga nuclear más alta y, en consecuencia, más electrones. La ocupación de los estados electrónicos en un átomo de este tipo puede predecirse mediante el principio de Aufbau y las reglas empíricas de Hund para los números cuánticos. El principio de Aufbau llena los orbitales en función de sus números cuánticos principales y azimutales (el más bajo primero, con los más bajos en los extremos; la regla de Hund favorece a los electrones desapareados en el orbital más externo). Estas reglas son empíricas, pero pueden relacionarse con la física electrónica. ^{[16] : 10  [17] : 260}${\displaystyle n+l}$${\displaystyle n}$

Si se tiene en cuenta la interacción espín-órbita , los operadores L y S ya no conmutan con el hamiltoniano y los estados propios del sistema ya no tienen un momento angular orbital y un espín bien definidos. Por lo tanto, se debería utilizar otro conjunto de números cuánticos. Este conjunto incluye ^{[18] [19]}

Por ejemplo, consideremos los siguientes 8 estados, definidos por sus números cuánticos:

	norte	ℓ	metro​	EM​		ℓ + s	ℓ − s	mℓ + ms​​
(1)	2	1	1	+ ⁠1/2⁠		⁠3/2⁠	⁠1/2⁠	⁠3/2⁠
(2)	2	1	1	− ⁠1/2⁠		⁠3/2⁠	⁠1/2⁠	⁠1/2⁠
(3)	2	1	0	+ ⁠1/2⁠		⁠3/2⁠	⁠1/2⁠	⁠1/2⁠
(4)	2	1	0	− ⁠1/2⁠		⁠3/2⁠	⁠1/2⁠	− ⁠1/2⁠
(5)	2	1	-1	+ ⁠1/2⁠		⁠3/2⁠	⁠1/2⁠	− ⁠1/2⁠
(6)	2	1	-1	− ⁠1/2⁠		⁠3/2⁠	⁠1/2⁠	− ⁠3/2⁠
(7)	2	0	0	+ ⁠1/2⁠		⁠1/2⁠	− ⁠1/2⁠	⁠1/2⁠
(8)	2	0	0	− ⁠1/2⁠		⁠1/2⁠	− ⁠1/2⁠	− ⁠1/2⁠

Los estados cuánticos del sistema pueden describirse como una combinación lineal de estos 8 estados. Sin embargo, en presencia de interacción espín-órbita , si se desea describir el mismo sistema mediante 8 estados que son vectores propios del hamiltoniano (es decir, cada uno representa un estado que no se mezcla con otros a lo largo del tiempo), se deben considerar los siguientes 8 estados:

yo	mj​	paridad
⁠3/2⁠	⁠3/2⁠	extraño	procedente del estado (1) anterior
⁠3/2⁠	⁠1/2⁠	extraño	procedentes de los estados (2) y (3) anteriores
⁠3/2⁠	− ⁠1/2⁠	extraño	procedentes de los estados (4) y (5) anteriores
⁠3/2⁠	− ⁠3/2⁠	extraño	procedente del estado (6) anterior
⁠1/2⁠	⁠1/2⁠	extraño	procedentes de los estados (2) y (3) anteriores
⁠1/2⁠	− ⁠1/2⁠	extraño	procedentes de los estados (4) y (5) anteriores
⁠1/2⁠	⁠1/2⁠	incluso	procedente del estado (7) anterior
⁠1/2⁠	− ⁠1/2⁠	incluso	procedente del estado (8) anterior

En los núcleos , todo el conjunto de protones y neutrones ( nucleones ) tiene un momento angular resultante debido a los momentos angulares de cada nucleón, generalmente denotado I. Si el momento angular total de un neutrón es j _n = ℓ + s y para un protón es j _p = ℓ + s (donde s para protones y neutrones resulta ser ⁠1/2⁠ de nuevo ( ver nota )), entonces los números cuánticos del momento angular nuclear I vienen dados por:

yo = | j _n − j _p |, | j _n − j _p | + 1, | j _n − j _p | + 2, ..., ( j _n + j _p ) − 2, ( j _n + j _p ) − 1, ( j _n + j _p )

Nota: Los momentos angulares orbitales de los estados nucleares (y atómicos) son todos múltiplos enteros de ħ, mientras que los momentos angulares intrínsecos del neutrón y el protón son múltiplos semienteros. Debería ser evidente de inmediato que la combinación de los espines intrínsecos de los nucleones con su movimiento orbital siempre dará valores semienteros para el espín total, I , de cualquier núcleo A impar y valores enteros para cualquier núcleo A par.

La paridad con el número I se utiliza para etiquetar los estados del momento angular nuclear; algunos ejemplos de isótopos de hidrógeno (H), carbono (C) y sodio (Na) son: ^[20]

1 1yo	Yo = ( ⁠1/2⁠ ) ​​+		9 6do	Yo = ( ⁠3/2⁠ ) ​​−		20 11N / A	Yo = 2 +
2 1yo	Yo = 1 +		10 6do	Yo = 0 +		21 11N / A	Yo = ( ⁠3/2⁠ ) ​​+
3 1yo	Yo = ( ⁠1/2⁠ ) ​​+		11 6do	Yo = ( ⁠3/2⁠ ) ​​−		22 11N / A	Yo = 3 +
			12 6do	Yo = 0 +		23 11N / A	Yo = ( ⁠3/2⁠ ) ​​+
			13 6do	Yo = ( ⁠1/2⁠ ) ​​−		24 11N / A	Yo = 4 +
			14 6do	Yo = 0 +		25 11N / A	Yo = ( ⁠5/2⁠ ) ​​+
			15 6do	Yo = ( ⁠1/2⁠ ) ​​+		26 11N / A	Yo = 3 +

La razón de las fluctuaciones inusuales en I , incluso por diferencias de solo un nucleón, se deben a los números pares e impares de protones y neutrones: los pares de nucleones tienen un momento angular total de cero (al igual que los electrones en orbitales), dejando un número par o impar de nucleones desapareados. La propiedad del espín nuclear es un factor importante para el funcionamiento de la espectroscopia de RMN en química orgánica , ^[19] y la RMN en medicina nuclear , ^[20] debido al momento magnético nuclear que interactúa con un campo magnético externo .

Las partículas elementales contienen muchos números cuánticos que, por lo general, se dice que les son intrínsecos. Sin embargo, debe entenderse que las partículas elementales son estados cuánticos del modelo estándar de física de partículas y, por lo tanto, los números cuánticos de estas partículas guardan la misma relación con el hamiltoniano de este modelo que los números cuánticos del átomo de Bohr con su hamiltoniano . En otras palabras, cada número cuántico denota una simetría del problema. En la teoría cuántica de campos es más útil distinguir entre el espacio-tiempo y las simetrías internas.

Los números cuánticos típicos relacionados con las simetrías del espacio-tiempo son el espín (relacionado con la simetría rotacional), la paridad , la paridad C y la paridad T (relacionadas con la simetría de Poincaré del espacio-tiempo ). Las simetrías internas típicas ^{[ aclaración necesaria ]} son ​​el número leptónico y el número bariónico o la carga eléctrica . (Para una lista completa de números cuánticos de este tipo, consulte el artículo sobre el sabor ).

La mayoría de los números cuánticos conservados son aditivos, por lo que en una reacción de partículas elementales, la suma de los números cuánticos debería ser la misma antes y después de la reacción. Sin embargo, algunos, generalmente llamados paridad , son multiplicativos; es decir, su producto se conserva. Todos los números cuánticos multiplicativos pertenecen a una simetría (como la paridad) en la que aplicar la transformación de simetría dos veces es equivalente a no hacer nada ( involución ).

• Configuración electrónica

• Dirac, Paul AM (1982). Principios de mecánica cuántica . Oxford University Press. ISBN 0-19-852011-5.
• Griffiths, David J. (2004). Introducción a la mecánica cuántica (2.ª ed.). Prentice Hall. ISBN 0-13-805326-X.
• Halzen, Francis y Martin, Alan D. (1984). Quarks y leptones: un curso introductorio a la física de partículas moderna . John Wiley & Sons. ISBN 0-471-88741-2.
• Eisberg, Robert Martin; Resnick, Robert (1985). Física cuántica de átomos, moléculas, sólidos, núcleos y partículas (2.ª ed.). John Wiley & Sons. ISBN 978-0-471-87373-0– vía Internet Archive .