Metamaterial

Un metamaterial (de la palabra griega μετά meta , que significa "más allá" o "después", y la palabra latina materia , que significa "materia" o "material") es un tipo de material diseñado para tener una propiedad, típicamente observada raramente en materiales naturales, que se deriva no de las propiedades de los materiales base sino de sus estructuras recientemente diseñadas. Los metamateriales generalmente se forman a partir de múltiples materiales, como metales y plásticos, y generalmente se organizan en patrones repetitivos , a escalas que son más pequeñas que las longitudes de onda de los fenómenos en los que influyen. Su forma precisa , geometría , tamaño , orientación y disposición les otorgan sus propiedades "inteligentes" de manipulación de ondas electromagnéticas , acústicas o incluso sísmicas: bloqueando, absorbiendo, mejorando o doblando las ondas, para lograr beneficios que van más allá de lo que es posible con los materiales convencionales.

Los metamateriales diseñados apropiadamente pueden afectar las ondas de radiación electromagnética o sonido de una manera no observada en materiales a granel. ^{[3] [4] [5]} Aquellos que exhiben un índice de refracción negativo para longitudes de onda particulares han sido el foco de una gran cantidad de investigación. ^{[6] [7] [8]} Estos materiales se conocen como metamateriales de índice negativo .

Las aplicaciones potenciales de los metamateriales son diversas e incluyen equipos deportivos ^{[9] [10]} filtros ópticos , dispositivos médicos , aplicaciones aeroespaciales remotas, detección de sensores y monitoreo de infraestructura , administración inteligente de energía solar , láseres, ^[11] control de multitudes , radomos , comunicación de campo de batalla de alta frecuencia y lentes para antenas de alta ganancia, mejora de sensores ultrasónicos e incluso blindaje de estructuras contra terremotos . ^{[12] [13] [14] [15]} Los metamateriales ofrecen el potencial de crear superlentes . ^[16] Una lente de este tipo puede permitir la obtención de imágenes por debajo del límite de difracción , que es la resolución mínima d = λ/(2NA) que se puede lograr con lentes convencionales que tienen una apertura numérica NA y con una longitud de onda de iluminación λ. Los metamateriales ópticos de sublongitud de onda, cuando se integran con medios de grabación óptica, se pueden utilizar para lograr una densidad de datos ópticos superior a la limitada por la difracción. ^[17] Se demostró una forma de "invisibilidad" utilizando materiales de índice de gradiente . Los metamateriales acústicos y sísmicos también son áreas de investigación. ^{[12] [18]}

La investigación sobre metamateriales es interdisciplinaria e involucra campos como la ingeniería eléctrica , el electromagnetismo , la óptica clásica , la física del estado sólido , la ingeniería de microondas y antenas , la optoelectrónica , las ciencias de los materiales , la nanociencia y la ingeniería de semiconductores . ^[4]

Las exploraciones de materiales artificiales para manipular ondas electromagnéticas comenzaron a fines del siglo XIX. Algunas de las primeras estructuras que pueden considerarse metamateriales fueron estudiadas por Jagadish Chandra Bose , quien en 1898 investigó sustancias con propiedades quirales . Karl Ferdinand Lindman estudió la interacción de las ondas con hélices metálicas como medios quirales artificiales a principios del siglo XX.

A finales de la década de 1940, Winston E. Kock de AT&T Bell Laboratories desarrolló materiales que tenían características similares a los metamateriales. En las décadas de 1950 y 1960, se estudiaron dieléctricos artificiales para antenas de microondas ligeras. En las décadas de 1980 y 1990, se investigaron los absorbedores de radar de microondas como aplicaciones para medios quirales artificiales. ^{[4] [19] [20]}

Los materiales de índice negativo fueron descritos teóricamente por primera vez por Victor Veselago en 1967. ^[21] Demostró que dichos materiales podían transmitir luz . Demostró que la velocidad de fase podía hacerse antiparalela a la dirección del vector de Poynting . Esto es contrario a la propagación de ondas en materiales naturales. ^[8]

En 1995, John M. Guerra fabricó una rejilla transparente de longitud de onda inferior (posteriormente llamada metamaterial fotónico) con líneas y espacios de 50 nm, y luego la acopló con un objetivo de microscopio de inmersión en aceite estándar (la combinación posteriormente llamada superlente) para resolver una rejilla en una oblea de silicio que también tenía líneas y espacios de 50 nm. Esta imagen superresuelta se logró con una iluminación con una longitud de onda de 650 nm en el aire. ^[16]

En 2000, John Pendry fue el primero en identificar una forma práctica de hacer un metamaterial zurdo, un material en el que no se sigue la regla de la mano derecha . ^[21] Un material de este tipo permite que una onda electromagnética transmita energía (tenga una velocidad de grupo ) en contra de su velocidad de fase . La idea de Pendry era que los cables metálicos alineados a lo largo de la dirección de una onda podrían proporcionar permitividad negativa ( función dieléctrica ε < 0). Los materiales naturales (como los ferroeléctricos ) muestran permitividad negativa; el desafío era lograr permeabilidad negativa (μ < 0). En 1999, Pendry demostró que un anillo partido (forma de C) con su eje colocado a lo largo de la dirección de propagación de la onda podía hacerlo. En el mismo artículo, demostró que una matriz periódica de cables y anillos podía dar lugar a un índice de refracción negativo. Pendry también propuso un diseño relacionado con la permeabilidad negativa, el rollo suizo .

En 2000, David R. Smith et al. informaron sobre la demostración experimental del funcionamiento de metamateriales electromagnéticos mediante el apilamiento horizontal, periódico , de resonadores de anillo dividido y estructuras de alambre delgado. En 2002 se proporcionó un método para realizar metamateriales de índice negativo utilizando líneas de transmisión cargadas con elementos concentrados artificiales en tecnología de microbanda . En 2003, se demostró el índice de refracción negativo complejo (tanto las partes reales como imaginarias de) ^[22] y la formación de imágenes mediante lentes planas ^[23] utilizando metamateriales zurdos. En 2007, muchos grupos habían realizado experimentos que involucraban un índice de refracción negativo . ^{[3] [15]} En frecuencias de microondas, en 2006 se realizó la primera capa de invisibilidad imperfecta. ^{[24] [25] [26] [27] [28]}

Desde el punto de vista de las ecuaciones que gobiernan, los investigadores contemporáneos pueden clasificar el reino de los metamateriales en tres ramas principales: ^[29] metamateriales de ondas electromagnéticas/ópticas, otros metamateriales de ondas y metamateriales de difusión . Estas ramas se caracterizan por sus respectivas ecuaciones de gobierno, que incluyen las ecuaciones de Maxwell (una ecuación de ondas que describe ondas transversales), otras ecuaciones de ondas (para ondas longitudinales y transversales) y ecuaciones de difusión (relativas a los procesos de difusión). ^[30] Diseñados para gobernar una gama de actividades de difusión, los metamateriales de difusión priorizan la longitud de difusión como su métrica central. Este parámetro crucial experimenta fluctuaciones temporales mientras permanece inmune a las variaciones de frecuencia. Por el contrario, los metamateriales de ondas, diseñados para ajustar varias trayectorias de propagación de ondas, consideran la longitud de onda de las ondas entrantes como su métrica esencial. Esta longitud de onda permanece constante a lo largo del tiempo, aunque se ajusta con alteraciones de frecuencia. Fundamentalmente, las métricas clave para la difusión y los metamateriales de ondas presentan una marcada divergencia, lo que subraya una clara relación complementaria entre ellos. Para obtener información completa, consulte la Sección IB, "Evolución de la física de metamateriales", en la Ref. ^{[29] .}

Artículos sobre
Electromagnetismo
Electricidad Magnetismo Óptica Historia Computacional Libros de texto Fenómenos
Electrostática Densidad de carga Conductor Ley de Coulomb Electreto Carga eléctrica Dipolo eléctrico Campo eléctrico Flujo eléctrico Potencial eléctrico Descarga electrostática Inducción electrostática Ley de Gauss Aislante Permitividad Polarización Energía potencial Electricidad estática Triboelectricidad
Magnetostática Ley de Ampère Ley de Biot-Savart Ley magnética de Gauss Dipolo magnético Campo magnético Flujo magnético Potencial escalar magnético Potencial vectorial magnético Magnetización Permeabilidad Regla de la mano derecha
Electrodinámica Radiación de frenado Radiación ciclotrónica Corriente de desplazamiento Corriente de Foucault Campo electromagnético Inducción electromagnética Pulso electromagnético Radiación electromagnética Ley de Faraday Ecuaciones de Jefimenko Fórmula de Larmor Ley de Lenz Potencial de Liénard-Wiechert Ecuaciones de Londres Fuerza de Lorentz Ecuaciones de Maxwell Tensor de Maxwell Vector de Poynting Radiación de sincrotrón
Red eléctrica Corriente alterna Capacidad Densidad de corriente Corriente continua Corriente eléctrica Energía eléctrica Electrólisis Fuerza electromotriz Impedancia Inductancia Calentamiento Joule Leyes de Kirchhoff Análisis de red Ley de Ohm Circuito paralelo Resistencia Cavidades resonantes Circuito en serie Voltaje Vatio Guías de ondas
Circuito magnético Motor de corriente alterna Motor de corriente continua Maquina electrica Motor eléctrico Condensador giratorio Motor de inducción Motor lineal Fuerza magnetomotriz Permeancia Renuencia (compleja) Renuencia (real) Rotor Estator Transformador
Formulación covariante Tensor electromagnético Electromagnetismo y relatividad especial Cuatro corrientes Cuatro potenciales Descripciones matemáticas Ecuaciones de Maxwell en el espacio-tiempo curvo Electromagnetismo relativista Tensor de estrés-energía
Científicos Amperio Biot Culombio David Einstein Faraday Fizeau Gauss Lado pesado Helmholtz Enrique Hertz Hopkinson Jefimenko Joule Kelvin Kirchhoff Larmor Lenz Liénard Lorentz Maxwell Neumann Ohm Ørsted Pescado Poynting Ritchie Sabor Cantante Piedras preciosas Tesla Thomson Vuelta Weber Wiechert
en a mi

Un metamaterial electromagnético se ve afectado por las ondas electromagnéticas que inciden o interactúan con sus características estructurales, que son más pequeñas que la longitud de onda. Para comportarse como un material homogéneo descrito con precisión por un índice de refracción efectivo , sus características deben ser mucho más pequeñas que la longitud de onda. ^{[ cita requerida ]}

Las propiedades inusuales de los metamateriales surgen de la respuesta resonante de cada elemento constituyente en lugar de su disposición espacial en una red. Permite considerar los parámetros materiales efectivos locales (permitividad y permeabilidad ). El efecto de resonancia relacionado con la disposición mutua de los elementos es responsable de la dispersión de Bragg , que subyace a la física de los cristales fotónicos , otra clase de materiales electromagnéticos. A diferencia de las resonancias locales, la dispersión de Bragg y la banda de detención de Bragg correspondiente tienen un límite de baja frecuencia determinado por el espaciado de la red. La aproximación de sublongitud de onda asegura que las bandas de detención de Bragg con los fuertes efectos de dispersión espacial estén en frecuencias más altas y puedan ignorarse. El criterio para desplazar la resonancia local por debajo de la banda de detención de Bragg inferior permite construir un diagrama de transición de fase fotónica en un espacio de parámetros, por ejemplo, tamaño y permitividad del elemento constituyente. Dicho diagrama muestra el dominio de los parámetros de estructura que permiten la observación de las propiedades del metamaterial en el material electromagnético. ^[31]

En el caso de la radiación de microondas , las características son del orden de milímetros . Los metamateriales de frecuencia de microondas suelen construirse como conjuntos de elementos conductores de electricidad (como bucles de alambre) que tienen características inductivas y capacitivas adecuadas . Muchos metamateriales de microondas utilizan resonadores de anillo dividido . ^{[5] [6]}

Los metamateriales fotónicos están estructurados a escala nanométrica y manipulan la luz a frecuencias ópticas. Los cristales fotónicos y las superficies selectivas de frecuencia, como las rejillas de difracción , los espejos dieléctricos y los revestimientos ópticos , presentan similitudes con los metamateriales estructurados a sublongitudes de onda . Sin embargo, estos suelen considerarse distintos de los metamateriales, ya que su función surge de la difracción o la interferencia y, por lo tanto, no pueden aproximarse como un material homogéneo. ^{[ cita requerida ]} Sin embargo, las estructuras de materiales como los cristales fotónicos son eficaces en el espectro de luz visible . La mitad del espectro visible tiene una longitud de onda de aproximadamente 560 nm (para la luz solar). Las estructuras de cristales fotónicos generalmente tienen la mitad de este tamaño o menos, es decir, < 280 nm. ^{[ cita requerida ]}

Los metamateriales plasmónicos utilizan plasmones de superficie , que son paquetes de carga eléctrica que oscilan colectivamente en las superficies de los metales a frecuencias ópticas.

Las superficies selectivas de frecuencia (FSS) pueden exhibir características de sublongitud de onda y se conocen como conductores magnéticos artificiales (AMC) o superficies de alta impedancia (HIS). Las FSS muestran características inductivas y capacitivas que están directamente relacionadas con su estructura de sublongitud de onda. ^[32]

Los metamateriales electromagnéticos se pueden dividir en diferentes clases, como sigue: ^{[3] [21] [4] [33]}

Los metamateriales de índice negativo (NIM) se caracterizan por un índice de refracción negativo. Otros términos para los NIM incluyen "medios levógiros", "medios con un índice de refracción negativo" y "medios de onda inversa". ^[3] Los NIM en los que el índice de refracción negativo surge de una permitividad y permeabilidad negativas simultáneas también se conocen como metamateriales doblemente negativos o materiales doblemente negativos (DNG). ^[21]

Suponiendo un material bien aproximado por una permitividad y permeabilidad reales, la relación entre permitividad , permeabilidad e índice de refracción n viene dada por . Todos los materiales transparentes no metamateriales conocidos (vidrio, agua, ...) poseen valores positivos y . Por convención, se utiliza la raíz cuadrada positiva para n . Sin embargo, algunos metamateriales diseñados tienen y . Debido a que el producto es positivo, n es real . En tales circunstancias, es necesario tomar la raíz cuadrada negativa para n . Cuando ambos y son positivos (negativos), las ondas viajan en dirección hacia adelante ( hacia atrás ). Las ondas electromagnéticas no pueden propagarse en materiales con y de signo opuesto ya que el índice de refracción se vuelve imaginario . Dichos materiales son opacos para la radiación electromagnética y los ejemplos incluyen materiales plasmónicos como metales ( oro , plata , ...).${\displaystyle \varepsilon _{r}}$ ${\displaystyle \mu _{r}}$ ${\textstyle n=\pm {\sqrt {\varepsilon _{\mathrm {r} }\mu _{\mathrm {r} }}}}$${\displaystyle \varepsilon _{r}}$${\displaystyle \mu _{r}}$${\displaystyle \varepsilon _{r}}$${\displaystyle \mu _{r}<0}$${\displaystyle \varepsilon _{r}\mu _{r}}$${\displaystyle \varepsilon _{r}}$${\displaystyle \mu _{r}}$${\displaystyle \varepsilon _{r}}$${\displaystyle \mu _{r}}$

Las consideraciones anteriores son simplistas para los materiales reales, que deben tener valores complejos de n y . Las partes reales de ambos y no tienen que ser negativas para que un material pasivo muestre refracción negativa. ^{[34] [35]} De hecho, un índice de refracción negativo para ondas polarizadas circularmente también puede surgir de la quiralidad. ^{[36] [37] Los metamateriales con} n negativo tienen numerosas propiedades interesantes: ^{[4] [38]}${\displaystyle \varepsilon _{r}}$${\displaystyle \mu _{r}}$${\displaystyle \varepsilon _{r}}$${\displaystyle \mu _{r}}$

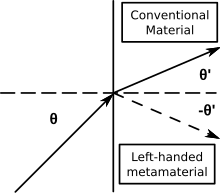
• La ley de Snell ( n ₁ sen θ ₁ = n ₂ sen θ ₂ ) todavía describe la refracción, pero como n ₂ es negativo, los rayos incidentes y refractados están en el mismo lado de la normal de la superficie en una interfaz de materiales de índice positivo y negativo.
• La radiación de Cherenkov apunta en la dirección opuesta. ^{[ Se necesita más explicación ]}
• El vector de Poynting promediado en el tiempo es antiparalelo a la velocidad de fase. Sin embargo, para que las ondas (energía) se propaguen, a – μ debe estar emparejado con a – ε para satisfacer la dependencia del número de onda de los parámetros del material .${\displaystyle kc=\omega {\sqrt {\mu \varepsilon }}}$

El índice de refracción negativo se deriva matemáticamente del triplete vectorial E , H y k . ^[4]

Para las ondas planas que se propagan en metamateriales electromagnéticos, el campo eléctrico, el campo magnético y el vector de onda siguen una regla de la mano izquierda , lo inverso del comportamiento de los materiales ópticos convencionales.

Hasta la fecha, sólo los metamateriales presentan un índice de refracción negativo. ^{[3] [38] [39]}

Los metamateriales negativos simples (SNG) tienen permitividad relativa negativa (ε r ) o permeabilidad relativa negativa (μ r ), pero no ambas. ^[21] Actúan como metamateriales cuando se combinan con un SNG complementario diferente, actuando conjuntamente como un DNG.

Los medios épsilon negativos (ENG) muestran un ε r negativo mientras que μ r es positivo. ^{[3] [38] [21]} Muchos plasmas exhiben esta característica. Por ejemplo, los metales nobles como el oro o la plata son ENG en los espectros infrarrojo y visible .

Los medios Mu-negativos (MNG) muestran un ε r positivo y un μ r negativo . ^{[3] [38] [21]} Los materiales girotrópicos o giromagnéticos exhiben esta característica. Un material girotrópico es uno que ha sido alterado por la presencia de un campo magnético cuasiestático , lo que permite un efecto magnetoóptico . ^{[ cita requerida ]} Un efecto magnetoóptico es un fenómeno en el que una onda electromagnética se propaga a través de dicho medio. En dicho material, las polarizaciones elípticas rotatorias hacia la izquierda y hacia la derecha pueden propagarse a diferentes velocidades. Cuando la luz se transmite a través de una capa de material magnetoóptico, el resultado se denomina efecto Faraday : el plano de polarización se puede rotar, formando un rotador de Faraday . Los resultados de dicha reflexión se conocen como efecto Kerr magnetoóptico (que no debe confundirse con el efecto Kerr no lineal ). Dos materiales girotrópicos con direcciones de rotación invertidas de las dos polarizaciones principales se denominan isómeros ópticos .

La unión de una placa de material ENG y una placa de material MNG dio como resultado propiedades como resonancias, efecto túnel anómalo, transparencia y reflexión cero. Al igual que los materiales de índice negativo, los SNG son dispersivos por naturaleza, por lo que sus ε r , μ r e índice de refracción n son una función de la frecuencia. ^[38]

Los metamateriales hiperbólicos (HMM) se comportan como un metal para cierta polarización o dirección de propagación de la luz y se comportan como un dieléctrico para el otro debido a los componentes tensoriales de permitividad negativos y positivos, lo que da lugar a una anisotropía extrema. La relación de dispersión del material en el espacio de vector de onda forma un hiperboloide y, por lo tanto, se denomina metamaterial hiperbólico. La anisotropía extrema de los HMM conduce a la propagación direccional de la luz dentro y sobre la superficie. ^[40] Los HMM han mostrado varias aplicaciones potenciales, como detección, modulación de reflexión, ^[41] formación de imágenes, dirección de señales ópticas y efectos mejorados de resonancia de plasmón. ^[42]

Los metamateriales con banda prohibida electromagnética (EBG o EBM) controlan la propagación de la luz. Esto se logra con cristales fotónicos (PC) o materiales zurdos (LHM). Los PC pueden prohibir la propagación de la luz por completo. Ambas clases pueden permitir que la luz se propague en direcciones específicas diseñadas y ambas pueden diseñarse con bandas prohibidas en las frecuencias deseadas. ^{[43] [44]} El tamaño del período de los EBG es una fracción apreciable de la longitud de onda, lo que crea interferencias constructivas y destructivas.

Los PC se distinguen de las estructuras de sublongitud de onda, como los metamateriales sintonizables , porque el PC deriva sus propiedades de sus características de banda prohibida. Los PC tienen un tamaño que coincide con la longitud de onda de la luz, a diferencia de otros metamateriales que exponen una estructura de sublongitud de onda. Además, los PC funcionan difractando la luz. Por el contrario, el metamaterial no utiliza la difracción. ^[45]

Los PC tienen inclusiones periódicas que inhiben la propagación de ondas debido a la interferencia destructiva de las inclusiones por dispersión. La propiedad de banda prohibida fotónica de los PC los convierte en el análogo electromagnético de los cristales semiconductores electrónicos. ^[46]

Los EBG tienen como objetivo crear estructuras dieléctricas periódicas, de baja pérdida y alta calidad. Un EBG afecta a los fotones de la misma manera que los materiales semiconductores afectan a los electrones. Los PC son el material de banda prohibida perfecto, porque no permiten la propagación de la luz. ^[47] Cada unidad de la estructura periódica prescrita actúa como un átomo, aunque de un tamaño mucho mayor. ^{[3] [47]}

Los EBG están diseñados para evitar la propagación de un ancho de banda asignado de frecuencias, para ciertos ángulos de llegada y polarizaciones . Se han propuesto varias geometrías y estructuras para fabricar las propiedades especiales de los EBG. En la práctica, es imposible construir un dispositivo EBG perfecto. ^{[3] [4]}

Los EBG se han fabricado para frecuencias que van desde unos pocos gigahercios (GHz) hasta unos pocos terahercios (THz), radio, microondas y regiones de frecuencias del infrarrojo medio. Los desarrollos de aplicaciones de EBG incluyen una línea de transmisión , pilas de leña hechas de barras dieléctricas cuadradas y varios tipos diferentes de antenas de baja ganancia . ^{[3] [4]}

Los medios doblemente positivos (DPS) existen en la naturaleza, como los dieléctricos naturales . La permitividad y la permeabilidad magnética son positivas y la propagación de las ondas se produce en dirección hacia adelante. Se han fabricado materiales artificiales que combinan las propiedades de los DPS, ENG y MNG. ^{[3] [21]}

La clasificación de los metamateriales en doble negativo o simple negativo, o doble positivo, normalmente supone que el metamaterial tiene respuestas eléctricas y magnéticas independientes descritas por ε y μ. Sin embargo, en muchos casos, el campo eléctrico causa polarización magnética , mientras que el campo magnético induce polarización eléctrica, conocida como acoplamiento magnetoeléctrico. Dichos medios se denominan bi-isotrópicos . Los medios que exhiben acoplamiento magnetoeléctrico y que son anisotrópicos (que es el caso de muchas estructuras de metamateriales ^[48] ), se denominan bianisótropos. ^{[49] [50]}

Cuatro parámetros materiales son intrínsecos al acoplamiento magnetoeléctrico de medios biisotrópicos. Son las intensidades de campo eléctrico ( E ) y magnético ( H ) , y las densidades de flujo eléctrico ( D ) y magnético ( B ) . Estos parámetros son ε, μ, κ y χ o permitividad, permeabilidad, fuerza de quiralidad y el parámetro Tellegen, respectivamente. En este tipo de medios, los parámetros materiales no varían con los cambios a lo largo de un sistema de coordenadas rotado de mediciones. En este sentido son invariantes o escalares . ^[4]

Los parámetros magnetoeléctricos intrínsecos, κ y χ , afectan la fase de la onda. El efecto del parámetro de quiralidad es dividir el índice de refracción. En medios isotrópicos, esto da como resultado la propagación de la onda solo si ε y μ tienen el mismo signo. En medios biisotrópicos con χ asumiendo que es cero y κ un valor distinto de cero, aparecen diferentes resultados. Puede ocurrir una onda hacia atrás o una onda hacia adelante. Alternativamente, pueden ocurrir dos ondas hacia adelante o dos ondas hacia atrás, dependiendo de la fuerza del parámetro de quiralidad.

En el caso general, las relaciones constitutivas para materiales bianisotrópicos se leen donde y son los tensores de permitividad y permeabilidad, respectivamente, mientras que y son los dos tensores magnetoeléctricos. Si el medio es recíproco, la permitividad y la permeabilidad son tensores simétricos, y , donde es el tensor quiral que describe la respuesta electromagnética quiral y magnetoeléctrica recíproca. El tensor quiral se puede expresar como , donde es la traza de , I es la matriz identidad, N es un tensor simétrico sin trazas, y J es un tensor antisimétrico. Tal descomposición nos permite clasificar la respuesta bianisotrópica recíproca y podemos identificar las siguientes tres clases principales: (i) medios quirales ( ), (ii) medios pseudoquirales ( ), (iii) medios omega ( ).${\displaystyle \mathbf {D} =\varepsilon \mathbf {E} +\xi \mathbf {H} ,}$${\displaystyle \mathbf {B} =\zeta \mathbf {E} +\mu \mathbf {H} ,}$${\displaystyle \varepsilon }$${\displaystyle \mu }$${\displaystyle \xi }$${\displaystyle \zeta }$${\displaystyle \xi =-\zeta ^{T}=-i\kappa ^{T}}$${\displaystyle \kappa }$${\displaystyle \kappa ={\tfrac {1}{3}}\operatorname {tr} (\kappa )I+N+J}$${\displaystyle \operatorname {tr} (\kappa )}$${\displaystyle \kappa }$${\displaystyle \operatorname {tr} (\kappa )\neq 0,N\neq 0,J=0}$${\displaystyle \operatorname {tr} (\kappa )=0,N\neq 0,J=0}$${\displaystyle \operatorname {tr} (\kappa )=0,N=0,J\neq 0}$

La lateralidad de los metamateriales es una fuente potencial de confusión, ya que la literatura sobre metamateriales incluye dos usos conflictivos de los términos "zurdo" y "diestro" . El primero se refiere a una de las dos ondas polarizadas circularmente que son los modos de propagación en medios quirales. El segundo se relaciona con el triplete de campo eléctrico, campo magnético y vector de Poynting que surgen en medios con índice de refracción negativo, que en la mayoría de los casos no son quirales.

Generalmente, una respuesta electromagnética quiral y/o bianisotrópica es una consecuencia de la quiralidad geométrica 3D: los metamateriales quirales 3D se componen mediante la incrustación de estructuras quirales 3D en un medio anfitrión y muestran efectos de polarización relacionados con la quiralidad, como actividad óptica y dicroísmo circular . También existe el concepto de quiralidad 2D y se dice que un objeto plano es quiral si no se puede superponer a su imagen especular a menos que se levante del plano. Se ha observado que los metamateriales quirales 2D que son anisotrópicos y con pérdidas exhiben transmisión direccionalmente asimétrica (reflexión, absorción) de ondas polarizadas circularmente debido al dicroísmo de conversión circular. ^{[51] [52]} Por otro lado, la respuesta bianisotrópica puede surgir de estructuras aquirales geométricas que no poseen quiralidad intrínseca 2D ni 3D. Plum y sus colegas investigaron el acoplamiento magnetoeléctrico debido a la quiralidad extrínseca , donde la disposición de una estructura (aquiral) junto con el vector de onda de radiación es diferente de su imagen especular, y observaron una gran actividad óptica lineal ajustable, ^[53] actividad óptica no lineal, ^[54] actividad óptica especular ^[55] y dicroísmo de conversión circular. ^[56] Rizza et al. ^[57] sugirieron metamateriales quirales 1D donde el tensor quiral efectivo no se desvanece si el sistema es geométricamente quiral unidimensional (la imagen especular de toda la estructura no se puede superponer sobre ella utilizando traslaciones sin rotaciones).

Los metamateriales quirales 3D se construyen a partir de materiales quirales o resonadores en los que el parámetro de quiralidad efectivo no es cero. Las propiedades de propagación de ondas en dichos metamateriales quirales demuestran que se puede lograr una refracción negativa en metamateriales con una quiralidad fuerte y una refracción positiva y . ^{[58] [59]} Esto se debe a que el índice de refracción tiene valores distintos para las ondas polarizadas circularmente izquierdas y derechas, dados por${\displaystyle \kappa }$${\displaystyle \varepsilon _{r}}$${\displaystyle \mu _{r}}$${\displaystyle n}$

${\displaystyle n=\pm {\sqrt {\varepsilon _{r}\mu _{r}}}\pm \kappa }$

Se puede observar que se producirá un índice negativo para una polarización si > . En este caso, no es necesario que uno o ambos y sean negativos para la propagación de ondas hacia atrás. ^{[4] Plum} et al. ^[36] y Zhang et al. ^[37] observaron por primera vez de forma simultánea e independiente un índice de refracción negativo debido a la quiralidad en 2009.${\displaystyle \kappa }$${\displaystyle {\sqrt {\varepsilon _{r}\mu _{r}}}}$${\displaystyle \varepsilon _{r}}$${\displaystyle \mu _{r}}$

Los metamateriales superficiales selectivos de frecuencia bloquean las señales en una banda de ondas y las dejan pasar en otra banda de ondas. Se han convertido en una alternativa a los metamateriales de frecuencia fija. Permiten cambios opcionales de frecuencias en un solo medio, en lugar de las limitaciones restrictivas de una respuesta de frecuencia fija . ^[60]

Estos metamateriales utilizan diferentes parámetros para lograr un índice de refracción negativo en materiales que no son electromagnéticos. Además, "un nuevo diseño de metamateriales elásticos que puedan comportarse como líquidos o sólidos en un rango de frecuencia limitado puede permitir nuevas aplicaciones basadas en el control de ondas acústicas, elásticas y sísmicas ". ^[61] También se les llama metamateriales mecánicos . ^{[ cita requerida ]}

Part of a series on
Continuum mechanics
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ Fick's laws of diffusion
Laws Conservations Mass Momentum Energy Inequalities Clausius–Duhem (entropy)
Solid mechanics Deformation Elasticity linear Plasticity Hooke's law Stress Strain Finite strain Infinitesimal strain Compatibility Bending Contact mechanics frictional Material failure theory Fracture mechanics
Fluid mechanics Fluids Statics · Dynamics Archimedes' principle · Bernoulli's principle Navier–Stokes equations Poiseuille equation · Pascal's law Viscosity (Newtonian · non-Newtonian) Buoyancy · Mixing · Pressure Liquids Adhesion Capillary action Chromatography Cohesion (chemistry) Surface tension Gases Atmosphere Boyle's law Charles's law Combined gas law Fick's law Gay-Lussac's law Graham's law Plasma
Rheology Viscoelasticity Rheometry Rheometer Smart fluids Electrorheological Magnetorheological Ferrofluids
Scientists Bernoulli Boyle Cauchy Charles Euler Fick Gay-Lussac Graham Hooke Newton Navier Noll Pascal Stokes Truesdell
v t e

Los metamateriales acústicos controlan, dirigen y manipulan el sonido en forma de ondas sónicas, infrasónicas o ultrasónicas en gases , líquidos y sólidos . Al igual que las ondas electromagnéticas, las ondas sónicas pueden presentar refracción negativa. ^[18]

El control de las ondas sonoras se logra principalmente a través del módulo volumétrico β , la densidad de masa ρ y la quiralidad. El módulo volumétrico y la densidad son análogos de la permitividad y la permeabilidad en metamateriales electromagnéticos. Relacionado con esto está la mecánica de propagación de ondas sonoras en una estructura reticular . Además, los materiales tienen masa y grados intrínsecos de rigidez . Juntos, estos forman un sistema resonante y la resonancia mecánica (sónica) puede ser excitada por frecuencias sónicas apropiadas (por ejemplo, pulsos audibles ).

Los metamateriales estructurales proporcionan propiedades como la capacidad de aplastamiento y el peso ligero. Mediante la microestereolitografía de proyección , se pueden crear microredes utilizando formas muy similares a cerchas y vigas . Se han creado materiales cuatro órdenes de magnitud más rígidos que el aerogel convencional , pero con la misma densidad. Dichos materiales pueden soportar una carga de al menos 160.000 veces su propio peso mediante una sobreconstricción de los materiales. ^{[62] [63]}

Un metamaterial de nanotruss cerámico se puede aplanar y volver a su estado original. ^[64]

Los materiales que se encuentran en la naturaleza, cuando son homogéneos, son isotrópicos térmicamente, es decir, el calor pasa a través de ellos aproximadamente a la misma velocidad en todas las direcciones. Sin embargo, los metamateriales térmicos son anisotrópicos, generalmente debido a su estructura interna altamente organizada. Los materiales compuestos con partículas o estructuras internas altamente alineadas, como las fibras y los nanotubos de carbono (CNT), son ejemplos de esto.

Se pueden fabricar metamateriales que incluyan alguna forma de medio no lineal , cuyas propiedades cambien con la potencia de la onda incidente. Los medios no lineales son esenciales para la óptica no lineal . La mayoría de los materiales ópticos tienen una respuesta relativamente débil, lo que significa que sus propiedades cambian solo una pequeña cantidad para grandes cambios en la intensidad del campo electromagnético . Los campos electromagnéticos locales de las inclusiones en metamateriales no lineales pueden ser mucho mayores que el valor promedio del campo. Además, se han predicho y observado efectos no lineales notables si la permitividad dieléctrica efectiva del metamaterial es muy pequeña (medio épsilon cercano a cero). ^{[65] [66] [67]} Además, propiedades exóticas como un índice de refracción negativo, crean oportunidades para adaptar las condiciones de coincidencia de fase que deben satisfacerse en cualquier estructura óptica no lineal.

Los metafluidos ofrecen propiedades programables, como viscosidad, compresibilidad y propiedades ópticas. Un enfoque empleó esferas de elastómero llenas de aire de 50 a 500 micrones de diámetro suspendidas en aceite de silicona . Las esferas se comprimen bajo presión y recuperan su forma cuando se alivia la presión. Sus propiedades difieren en esos dos estados. Sin presión, dispersan la luz, lo que las hace opacas. Bajo presión, colapsan en formas de media luna, enfocando la luz y volviéndose transparentes. La respuesta a la presión podría permitirles actuar como un sensor o como un fluido hidráulico dinámico. Al igual que el almidón de maíz , puede actuar como un fluido newtoniano o no newtoniano. Bajo presión, se vuelve no newtoniano, lo que significa que su viscosidad cambia en respuesta a la fuerza de corte. ^[68]

En 2009, Marc Briane y Graeme Milton ^[69] demostraron matemáticamente que, en principio, se puede invertir el signo de un compuesto basado en 3 materiales en 3D hecho únicamente con materiales con coeficiente Hall de signo positivo o negativo. Más tarde, en 2015, Muamer Kadic et al. ^[70] demostraron que una simple perforación de material isotrópico puede provocar un cambio de signo del coeficiente Hall. Esta afirmación teórica fue finalmente demostrada experimentalmente por Christian Kern et al. ^[71].

En 2015, Christian Kern et al. también demostraron que una perforación anisotrópica de un solo material puede provocar un efecto aún más inusual, el efecto Hall paralelo. ^[72] Esto significa que el campo eléctrico inducido dentro de un medio conductor ya no es ortogonal a la corriente y al campo magnético, sino que en realidad es paralelo a este último.

Los metabiomateriales han sido diseñados con el propósito de interactuar con los sistemas biológicos, fusionando principios tanto de la ciencia de los metamateriales como de las áreas biológicas. Diseñados a escala nanométrica, estos materiales manipulan hábilmente las propiedades electromagnéticas, acústicas o térmicas para facilitar los procesos biológicos. Mediante un ajuste meticuloso de su estructura y composición, los metabiomateriales son prometedores para aumentar diversas tecnologías biomédicas, como la obtención de imágenes médicas, ^[73] la administración de fármacos ^[74] y la ingeniería de tejidos. ^[75] Esto subraya la importancia de comprender los sistemas biológicos a través de la lente interdisciplinaria de la ciencia de los materiales.

Los metamateriales de terahercios interactúan en frecuencias de terahercios , generalmente definidas como de 0,1 a 10 THz . La radiación de terahercios se encuentra en el extremo más alejado de la banda infrarroja, justo después del final de la banda de microondas. Esto corresponde a longitudes de onda milimétricas y submilimétricas entre los 3 mm ( banda EHF ) y los 0,03 mm (borde de longitud de onda larga de la luz infrarroja lejana ).

Los metamateriales fotónicos interactúan con frecuencias ópticas ( infrarrojo medio ). El período de sublongitud de onda los distingue de las estructuras de banda prohibida fotónica . ^{[76] [77]}

Los metamateriales ajustables permiten realizar ajustes arbitrarios a los cambios de frecuencia en el índice de refracción. Un metamaterial ajustable se expande más allá de las limitaciones de ancho de banda de los materiales para zurdos mediante la construcción de varios tipos de metamateriales.

Los metamateriales plasmónicos explotan los plasmones de superficie , que se producen a partir de la interacción de la luz con dieléctricos metálicos. En condiciones específicas, la luz incidente se acopla con los plasmones de superficie para crear ondas electromagnéticas u ondas de superficie autosostenibles y que se propagan ^[78], conocidas como polaritones de plasmón de superficie . Las oscilaciones de plasma en masa hacen posible el efecto de masa negativa (densidad). ^{[79] [80]}

Los metamateriales se están considerando para muchas aplicaciones. ^[81] Las antenas de metamateriales están disponibles comercialmente.

En 2007, un investigador afirmó que para que se puedan realizar aplicaciones de metamateriales, se debe reducir la pérdida de energía, los materiales se deben extender a materiales isotrópicos tridimensionales y las técnicas de producción se deben industrializar. ^[82]

Las antenas metamateriales son una clase de antenas que utilizan metamateriales para mejorar el rendimiento. ^{[15] [21] [83] [84] Las demostraciones mostraron que los metamateriales podrían mejorar} la potencia radiada de una antena . ^{[15] [85]} Los materiales que pueden alcanzar permeabilidad negativa permiten propiedades como tamaño de antena pequeño, alta directividad y frecuencia sintonizable. ^{[15] [21]}

Un absorbedor de metamateriales manipula los componentes de pérdida de la permitividad y la permeabilidad magnética de los metamateriales, para absorber grandes cantidades de radiación electromagnética . ^[86] Esta es una característica útil para la fotodetección ^{[87] [88]} y aplicaciones solares fotovoltaicas . ^[89] Los componentes de pérdida también son relevantes en aplicaciones de índice de refracción negativo (metamateriales fotónicos, sistemas de antena) u óptica de transformación ( encubrimiento de metamateriales , mecánica celeste), pero a menudo no se utilizan en estas aplicaciones.

Una superlente es un dispositivo bidimensional o tridimensional que utiliza metamateriales, generalmente con propiedades de refracción negativas, para lograr una resolución más allá del límite de difracción (idealmente, una resolución infinita). Este comportamiento es posible gracias a la capacidad de los materiales doblemente negativos de producir una velocidad de fase negativa. El límite de difracción es inherente a los dispositivos ópticos o lentes convencionales. ^{[90] [91]}

Los metamateriales son una base potencial para un dispositivo de camuflaje práctico . La prueba de principio se demostró el 19 de octubre de 2006. No se conoce públicamente la existencia de camuflajes prácticos. ^{[92] [93] [94] [95] [96] [97]}

Los metamateriales tienen aplicaciones en la tecnología furtiva , que reduce la RCS de varias maneras (por ejemplo, absorción, difusión, redirección). Convencionalmente, la RCS se ha reducido ya sea mediante material absorbente de radar (RAM) o mediante la conformación intencionada de los objetivos de modo que la energía dispersa pueda redirigirse lejos de la fuente. Si bien los RAM tienen una funcionalidad de banda de frecuencia estrecha, la conformación intencionada limita el rendimiento aerodinámico del objetivo. Más recientemente, se sintetizan metamateriales o metasuperficies que pueden redirigir la energía dispersa lejos de la fuente utilizando la teoría de matrices ^{[98] [99] [100] [101]} o la ley de Snell generalizada. ^{[102] [103]} Esto ha llevado a formas aerodinámicamente favorables para los objetivos con la RCS reducida.

Los metamateriales sísmicos contrarrestan los efectos adversos de las ondas sísmicas sobre las estructuras construidas por el hombre. ^{[12] [104] [105]}

Los metamateriales texturizados con arrugas a escala nanométrica podrían controlar las señales de luz o sonido, por ejemplo, cambiando el color de un material o mejorando la resolución de ultrasonidos . Los usos incluyen pruebas de materiales no destructivas , diagnósticos médicos y supresión de sonido . Los materiales se pueden fabricar mediante un proceso de deposición multicapa de alta precisión. El espesor de cada capa se puede controlar con una precisión de una fracción de longitud de onda. Luego, el material se comprime, creando arrugas precisas cuyo espaciado puede causar la dispersión de frecuencias seleccionadas. ^{[106] [107]}

Los metamateriales se pueden integrar con guías de ondas ópticas para adaptar las ondas electromagnéticas guiadas ( meta-guía de ondas ). ^[108] Las estructuras de sublongitud de onda como los metamateriales se pueden integrar, por ejemplo, con guías de ondas de silicio para desarrollar divisores de haz de polarización ^[109] y acopladores ópticos, ^[110] añadiendo nuevos grados de libertad para controlar la propagación de la luz a escala nanométrica para dispositivos fotónicos integrados. ^[111] Se pueden desarrollar otras aplicaciones como convertidores de modo integrados, ^[112] (de)multiplexores de polarización, ^[113] generación de luz estructurada, ^[114] y biosensores en chip ^[115] . ^[108]

Todos los materiales están hechos de átomos , que son dipolos . Estos dipolos modifican la velocidad de la luz por un factor n (el índice de refracción). En un resonador de anillo dividido, las unidades de anillo y alambre actúan como dipolos atómicos: el alambre actúa como un átomo ferroeléctrico , mientras que el anillo actúa como un inductor L, mientras que la sección abierta actúa como un condensador C. El anillo en su conjunto actúa como un circuito LC . Cuando el campo electromagnético pasa a través del anillo, se crea una corriente inducida. El campo generado es perpendicular al campo magnético de la luz. La resonancia magnética da como resultado una permeabilidad negativa; el índice de refracción también es negativo. (La lente no es verdaderamente plana, ya que la capacitancia de la estructura impone una pendiente para la inducción eléctrica).

Varios modelos materiales (matemáticos) modelan la respuesta de frecuencia en los DNG. Uno de ellos es el modelo de Lorentz , que describe el movimiento de los electrones en términos de un oscilador armónico amortiguado y accionado . El modelo de relajación de Debye se aplica cuando el componente de aceleración del modelo matemático de Lorentz es pequeño en comparación con los otros componentes de la ecuación. El modelo de Drude se aplica cuando el componente de fuerza restauradora es insignificante y el coeficiente de acoplamiento es generalmente la frecuencia del plasma . Otras distinciones de componentes requieren el uso de uno de estos modelos, dependiendo de su polaridad o propósito. ^[3]

Los compuestos tridimensionales de inclusiones metálicas y no metálicas incrustadas de forma periódica o aleatoria en una matriz de baja permitividad suelen modelarse mediante métodos analíticos, incluidas fórmulas de mezcla y métodos basados ​​en matrices de dispersión. La partícula se modela mediante un dipolo eléctrico paralelo al campo eléctrico o un par de dipolos eléctricos y magnéticos cruzados paralelos a los campos eléctrico y magnético, respectivamente, de la onda aplicada. Estos dipolos son los términos principales de la serie multipolar. Son los únicos existentes para una esfera homogénea, cuya polarizabilidad se puede obtener fácilmente a partir de los coeficientes de dispersión de Mie . En general, este procedimiento se conoce como "aproximación de punto-dipolo", que es una buena aproximación para metamateriales que consisten en compuestos de esferas eléctricamente pequeñas. Las ventajas de estos métodos incluyen un bajo costo de cálculo y simplicidad matemática. ^{[116] [117]}

Tres conceptos: medio de índice negativo, cristal no reflectante y superlente son los fundamentos de la teoría de metamateriales. Otras técnicas de principios básicos para analizar medios electromagnéticos triplemente periódicos se pueden encontrar en Cálculo de la estructura de bandas fotónicas

La Iniciativa de Investigación Universitaria Multidisciplinaria (MURI) abarca docenas de universidades y algunas organizaciones gubernamentales. Entre las universidades participantes se encuentran la UC Berkeley, la UC Los Ángeles, la UC San Diego, el Instituto Tecnológico de Massachusetts y el Imperial College de Londres. Los patrocinadores son la Oficina de Investigación Naval y la Agencia de Proyectos de Investigación Avanzada de Defensa . ^[118]

El MURI apoya la investigación que combina más de una disciplina científica y de ingeniería tradicional para acelerar tanto la investigación como su aplicación. En 2009, se esperaba que 69 instituciones académicas participaran en 41 iniciativas de investigación. ^[119]

El Instituto Virtual de Materiales Electromagnéticos Artificiales y Metamateriales "Metamorphose VI AISBL" es una asociación internacional para promover los materiales electromagnéticos artificiales y los metamateriales. Organiza conferencias científicas, apoya revistas especializadas, crea y gestiona programas de investigación, ofrece programas de formación (incluidos programas de doctorado y de formación para socios industriales) y transferencia de tecnología a la industria europea. ^{[120] [121]}

• Metasuperficie
• Dieléctricos artificiales : análogos macroscópicos de dieléctricos naturales que comenzaron a utilizarse con las tecnologías de microondas por radar desarrolladas entre los años 1940 y 1970.
• METATOY ( Metamaterial para rayos ): compuesto de estructuras de longitud de onda superlarga, como pequeñas matrices de prismas y lentes, y puede operar en una amplia banda de frecuencias .
• Magnónica
• Metamateriales (revista)
• Manual de metamateriales
• Metamateriales: Exploraciones en Física e Ingeniería

• Medios relacionados con Metamateriales en Wikimedia Commons