Gran antiprisma
| Gran antiprisma | |
|---|---|
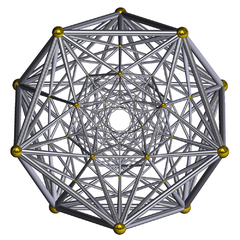 ( Diagrama de Schlegel en estructura alámbrica) | |
| Tipo | Politopo 4 uniforme |
| Índice uniforme | 47 |
| Células | 100+200 ( 3.3.3 ) 20 ( 3.3.3.5 )  |
| Caras | 20 {5} 700 {3} |
| Bordes | 500 |
| Vértices | 100 |
| Figura de vértice | Esfenocorona |
| Grupo de simetría | Grupo de Coxeter disminuido iónico [[10,2 + ,10]] de orden 400 |
| Propiedades | convexo |
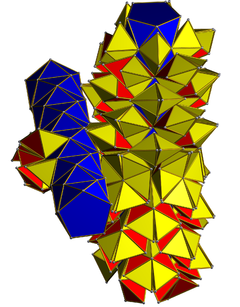 Una red que muestra dos anillos disjuntos de 10 antiprismas. 200 tetraedros (amarillos) están en contacto frontal con los antiprismas y 100 tetraedros (rojos) entran en contacto solo con otros tetraedros. | |
En geometría , el gran antiprisma o antiprismoide doble pentagonal es un 4-politopo uniforme ( politopo uniforme de 4 dimensiones ) limitado por 320 celdas : 20 antiprismas pentagonales y 300 tetraedros . Es un 4-politopo uniforme anómalo, no wythoffiano , descubierto en 1965 por Conway y Guy . [1] [2] Topológicamente, bajo su simetría más alta, los antiprismas pentagonales tienen simetría D 5d y hay dos tipos de tetraedros, uno con simetría S 4 y otro con simetría C s .
Nombres alternativos
- Antiprismoide doble pentagonal Norman W. Johnson
- Gap (Jonathan Bowers: por el gran antiprisma) [3]
Estructura
Se encuentran 20 antiprismas pentagonales apilados en dos anillos disjuntos de 10 antiprismas cada uno. Los antiprismas de cada anillo están unidos entre sí a través de sus caras pentagonales. Los dos anillos son mutuamente perpendiculares, en una estructura similar a un duoprisma .
Los 300 tetraedros unen los dos anillos entre sí y están dispuestos en una disposición bidimensional topológicamente equivalente al toro de 2 caras y la cresta del duocilindro . Estos se pueden dividir en tres conjuntos: 100 se aparean con un anillo, 100 se aparean con el otro anillo y 100 están centrados en el punto medio exacto del duocilindro y se aparean por arista con ambos anillos. Este último conjunto forma un toro plano y se puede "desenrollar" en una matriz cuadrada plana de 10 × 10 de tetraedros que se encuentran solo en sus aristas y vértices. Vea la figura a continuación.

Además, los 300 tetraedros se pueden dividir en 10 hélices de Boerdijk-Coxeter disjuntas de 30 celdas cada una, que se cierran una sobre la otra. Los dos tubos antiprismáticos pentagonales, más las 10 hélices BC, forman una fibración de Hopf discreta irregular del gran antiprisma que Hopf asigna a las caras de un antiprisma pentagonal. Los dos tubos se asignan a las dos caras pentagonales y las 10 hélices BC se asignan a las 10 caras triangulares.
La estructura del gran antiprisma es análoga a la de los antiprismas tridimensionales . Sin embargo, el gran antiprisma es el único análogo uniforme convexo del antiprisma en cuatro dimensiones (aunque el de 16 celdas puede considerarse un análogo regular del antiprisma digonal ). El único análogo uniforme no convexo de antiprisma tetradimensional utiliza antiprismas cruzados pentagrammicos en lugar de antiprismas pentagonales, y se denomina antiprismoide doble pentagrammico .
Figura de vértice
La figura del vértice del gran antiprisma es una esfenocorona o icosaedro regular diseccionado : un icosaedro regular al que se le han quitado dos vértices adyacentes. En su lugar se sustituyen 8 triángulos por un par de trapecios de aristas φ, 1, 1, 1 (donde φ es la proporción áurea ), unidos entre sí por su arista de longitud φ, para dar un tetradecaedro cuyas caras son los 2 trapecios y los 12 triángulos equiláteros restantes .
 12 ( 3.3.3 ) |  2 ( 3.3.3.5 ) |  Icosaedro regular diseccionado |
Construcción

El gran antiprisma puede construirse disminuyendo las 600 celdas : restando 20 pirámides cuyas bases son antiprismas pentagonales tridimensionales. A la inversa, los dos anillos de antiprismas pentagonales del gran antiprisma pueden triangularse mediante 10 tetraedros unidos a las caras triangulares de cada antiprisma, y un círculo de 5 tetraedros entre cada par de antiprismas, uniendo los 10 tetraedros de cada uno, obteniéndose 150 tetraedros por anillo. Estos, combinados con los 300 tetraedros que unen los dos anillos, dan como resultado los 600 tetraedros del modelo de 600 celdas.
Esta disminución se puede lograr quitando dos anillos de 10 vértices de la celda de 600, cada uno de ellos en planos mutuamente ortogonales. Cada anillo de vértices eliminados crea una pila de antiprismas pentagonales en la envoltura convexa . Esta relación es análoga a cómo se puede construir un antiprisma pentagonal a partir de un icosaedro quitando dos vértices opuestos, eliminando así 5 triángulos de los "polos" opuestos del icosaedro, dejando los 10 triángulos ecuatoriales y dos pentágonos en la parte superior e inferior.
(La pirámide de 24 celdas también se puede construir mediante otra disminución de la de 600 celdas, eliminando 24 pirámides icosaédricas. De manera equivalente, esto se puede realizar tomando la envoltura convexa de los vértices restantes después de que 24 vértices, correspondientes a los de una pirámide inscrita de 24 celdas , se eliminan de la de 600 celdas).
Alternativamente, también se puede construir a partir del ditetragoltriato decagonal (la envoltura convexa de dos duoprismas perpendiculares no uniformes 10-10 donde la razón de los dos decágonos está en la proporción áurea ) mediante un proceso de alternancia . Los prismas decagonales se alternan en antiprismas pentagonales , los trapezoprismas rectangulares se alternan en tetraedros con dos nuevos tetraedros regulares (que representan una bipirámide triangular no coreálmica ) creados en los vértices eliminados. Esta es la única solución uniforme para los antiprismoides dobles p-gonales junto con su conjugado, el antiprismoide doble pentagrammico del ditetragoltriato decagrammico.
| 600 celdas | Gran antiprisma |
|---|---|
| Avión H 4 Coxeter | |
 | 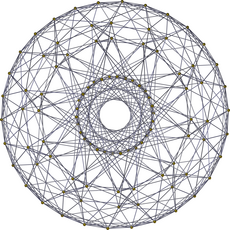 |
| 20-gonal | |
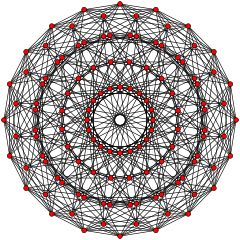 |  |
| Avión H 3 Coxeter (ligeramente desplazado) | |
 | |
Proyecciones
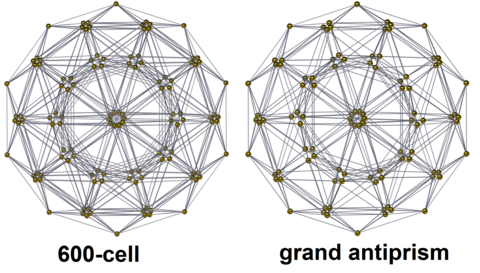
Se trata de dos proyecciones en perspectiva, proyectando el politopo en una hiperesfera y aplicando una proyección estereográfica en el espacio tridimensional.
 Estructura alámbrica, vista desde abajo por una de las columnas del antiprisma pentagonal. |  con caras triangulares transparentes |
 Proyección ortográfica centrada en el hiperplano de un antiprisma en uno de los dos anillos. | 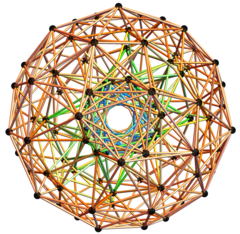 Proyección ortográfica 3D de 100 de 120 vértices de 600 celdas y 500 aristas {488 de 1/2 (3-Sqrt[5]) y 12 de 2/(3+Sqrt[5])}. |
Véase también
Notas
- ^ JH Conway y MJT Guy : Politopos arquimedianos de cuatro dimensiones , Actas del Coloquio sobre convexidad en Copenhague, páginas 38 y 39, 1965. (Michael Guy es hijo de Richard K. Guy )
- ^ Conway, 2008, p.402-403 El Gran Antiprisma
- ^ Klitzing, Richard. "Gran antiprisma de policora convexa 4D".
Referencias
- Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591] 2.8 El gran antiprisma
- Policorono uniforme convexo anómalo - Modelo 47, George Olshevsky.
- Klitzing, Richard. "Brecha de politopos uniformes 4D (policora)".
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 (Capítulo 26) El gran antiprisma
- Gran antiprisma y cuaterniones [1] Mehmet Koca, Mudhahir Al-Ajmi, Nazife Ozdes Koca (2009); Mehmet Koca et al. 2009 J. Física. R: Matemáticas. Teor. 42 495201
Enlaces externos
- En el vientre del gran antiprisma Archivado el 7 de febrero de 2006 en Wayback Machine (sección central, que describe la analogía con el icosaedro y el antiprisma pentagonal)