5 celdas

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "5-cell" – news · newspapers · books · scholar · JSTOR (August 2024) (Learn how and when to remove this message)

This article may contain an excessive amount of intricate detail that may interest only a particular audience. Please help by spinning off or relocating any relevant information, and removing excessive detail that may be against Wikipedia's inclusion policy. (August 2024) (Learn how and when to remove this message)

5 celdas (4-símplex)
Una proyección 3D de un sistema de 5 celdas que realiza una rotación simple
Tipo	Politopo cuatripartito regular convexo
Símbolo de Schläfli	{3,3,3}
Diagrama de Coxeter
Células	5 {3,3}
Caras	10 {3}
Bordes	10
Vértices	5
Figura de vértice	( tetraedro )
Polígono de Petrie	pentágono
Grupo Coxeter	Un 4 , [3,3,3]
Dual	Auto-dual
Propiedades	convexo , isogonal , isotoxal , isoédrico
Índice uniforme	1

En geometría , la 5-celda es el 4-politopo convexo con símbolo de Schläfli {3,3,3}. Es un objeto cuatridimensional de 5 vértices limitado por cinco celdas tetraédricas. También se conoce como C ₅ , hipertetraedro , ' pentacorono , ^[1] pentatopo , pentaedroide , ^[2] pirámide tetraédrica o 4- símplex (politopo de Coxeter ), ^[3] el 4-politopo convexo más simple posible, y es análogo al tetraedro en tres dimensiones y al triángulo en dos dimensiones. La 5-celda es una pirámide cuatridimensional con una base tetraédrica y cuatro lados tetraédricos.${\displaystyle \alpha _{4}}$

El tetraedro regular de 5 celdas está limitado por cinco tetraedros regulares y es uno de los seis tetrapolitopos convexos regulares (los análogos cuatridimensionales de los sólidos platónicos ). Se puede construir un tetraedro regular de 5 celdas a partir de un tetraedro regular añadiendo un quinto vértice a una longitud de arista de distancia de todos los vértices del tetraedro. Esto no se puede hacer en el espacio tridimensional. El tetraedro regular de 5 celdas es una solución al problema: hacer 10 triángulos equiláteros, todos del mismo tamaño, usando 10 cerillas, donde cada lado de cada triángulo sea exactamente una cerilla, y ninguno de los triángulos y cerillas se intersequen entre sí. No existe ninguna solución en tres dimensiones.

La 5-celda es el símplex de 4 dimensiones , el 4-politopo más simple posible . En otras palabras, la 5-celda es un policoro análogo a un tetraedro en alta dimensión. ^[4] Está formado por cinco puntos cualesquiera que no estén todos en el mismo hiperplano (como un tetraedro está formado por cuatro puntos cualesquiera que no estén todos en el mismo plano, y un triángulo está formado por tres puntos cualesquiera que no estén todos en la misma línea). Cualquiera de estos cinco puntos constituye una 5-celda, aunque normalmente no es una 5-celda regular. La 5-celda regular no se encuentra dentro de ninguno de los otros 4-politopos convexos regulares excepto uno: la 120-celda de 600 vértices es un compuesto de 120 5-celdas regulares.

La celda 5 es autodual , lo que significa que su politopo dual es la celda 5 en sí. ^[5] Su intersección máxima con el espacio tridimensional es el prisma triangular . Su ángulo dicoral es . ^[6]${\textstyle \arccos(-1/4)\approx 75.52^{\circ }}$

Es el primero de una secuencia de 6 4-politopos regulares convexos, en orden de volumen en un radio o número de vértices dado. ^[7]

La envoltura convexa de dos celdas de 5 en configuración dual es la celda diesfenoidal de 30 celdas , dual de la celda bitruncada de 5 celdas .

Esta matriz de configuración representa las 5 celdas. Las filas y columnas corresponden a los vértices, aristas, caras y celdas. Los números diagonales indican cuántos elementos de cada una de las 5 celdas hay. Los números no diagonales indican cuántos elementos de la columna hay en el elemento de la fila o en él. La matriz de este politopo autodual es idéntica a su rotación de 180 grados. ^[8] Las k -caras se pueden leer como filas a la izquierda de la diagonal, mientras que las k -figuras se leen como filas después de la diagonal. ^[9]

Elemento	k -cara	por favor	o0​	el 1	el 2	F3​	k -figs
	( )	o0​	5	4	6	4	{3,3}
	{ }	el 1	2	10	3	3	{3}
	{3}	el 2	3	3	10	2	{ }
	{3,3}	F3​	4	6	4	5	( )

Todos estos elementos de la celda de 5 están enumerados en el diagrama de Venn de 5 puntos de Branko Grünbaum , que es literalmente una ilustración de la celda de 5 regular en proyección al plano.

La celda de 5 celdas tiene solo planos centrales digon a través de vértices. Tiene 10 planos centrales digon, donde cada par de vértices es una arista, no un eje, de la celda de 5 celdas. Cada plano digon es ortogonal a otros 3, pero completamente ortogonal a ninguno de ellos. La rotación isoclínica característica de la celda de 5 celdas tiene, como pares de planos invariantes, esos 10 planos digon y sus planos centrales completamente ortogonales, que son planos 0-gonos que no intersecan ningún vértice de la celda de 5 celdas.

Sólo hay dos maneras de hacer un circuito de la celda de 5 a través de los 5 vértices a lo largo de 5 aristas, por lo que hay dos fibraciones de Hopf discretas de los grandes dígonos de la celda de 5. Cada una de las dos fibraciones corresponde a un par de rotaciones isoclínicas izquierda-derecha, cada una de las cuales rota los 5 vértices en un circuito de período 5. La celda de 5 tiene sólo dos isoclinas de período 5 distintas (esos círculos a través de los 5 vértices), cada una de las cuales actúa como la isoclina única de una rotación hacia la derecha y la isoclina única de una rotación hacia la izquierda en dos fibraciones diferentes.

A continuación, se visualiza un sistema de cinco celdas giratorio con la cuarta dimensión comprimida y mostrada en color. El toro de Clifford se representa en su forma rectangular (envolvente).

• Visualización de rotaciones 4D
• Simplemente girando en el plano XY
• Simplemente girando en el plano ZW
• Doble rotación en los planos XY y ZW con velocidades angulares en una relación 4:3
• Rotación isoclínica izquierda
• Rotación isoclínica derecha

El plano de Coxeter A ₄ proyecta el sistema de 5 celdas en un pentágono y un pentagrama regulares . La proyección del plano de Coxeter A _{3 del sistema de 5 celdas es la de una} pirámide cuadrada . La proyección del plano de Coxeter A ₂ del sistema de 5 celdas regular es la de una bipirámide triangular (dos tetraedros unidos cara a cara) con los dos vértices opuestos centrados.

proyecciones ortográficas

Un avión de Coxeter	Un 4	Un 3	Un 2
Gráfico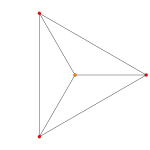
Simetría diedral	[5]	[4]	[3]

Proyecciones a 3 dimensiones
La proyección de vértice primero de la celda de 5 en 3 dimensiones tiene una envolvente de proyección tetraédrica . El vértice más cercano de la celda de 5 se proyecta hacia el centro del tetraedro, como se muestra aquí en rojo. La celda más alejada se proyecta hacia la propia envolvente tetraédrica, mientras que las otras 4 celdas se proyectan hacia las 4 regiones tetraédricas aplanadas que rodean el vértice central.	La proyección de la arista de la celda de 5 en 3 dimensiones tiene una envoltura bipiramidal triangular . La arista más cercana (mostrada aquí en rojo) se proyecta hacia el eje de la bipirámide, y las tres celdas que la rodean se proyectan hacia 3 volúmenes tetraédricos dispuestos alrededor de este eje a 120 grados entre sí. Las 2 celdas restantes se proyectan hacia las dos mitades de la bipirámide y están en el lado más alejado del pentátopo.
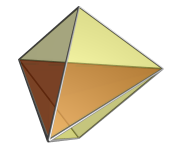La proyección de caras primero de la celda de 5 dimensiones en 3 dimensiones también tiene una envoltura bipiramidal triangular. La cara más cercana se muestra aquí en rojo. Las dos celdas que se encuentran en esta cara se proyectan hacia las dos mitades de la bipirámide. Las tres celdas restantes están en el lado más alejado del pentátopo desde el punto de vista 4D y se han eliminado de la imagen para mayor claridad. Están dispuestas alrededor del eje central de la bipirámide, al igual que en la proyección de aristas primero.	La proyección de la celda de 5 en 3 dimensiones tiene una envoltura tetraédrica. La celda más cercana se proyecta sobre toda la envoltura y, desde el punto de vista 4D, oculta las otras 4 celdas; por lo tanto, no se representan aquí.

En el caso de símplex como el de 5 celdas, ciertas formas irregulares son en cierto sentido más fundamentales que la forma regular. Aunque las 5 celdas regulares no pueden llenar el espacio de 4 ni los 4 politopos regulares, hay 5 celdas irregulares que sí lo hacen. Estas 5 celdas características son los dominios fundamentales de los diferentes grupos de simetría que dan lugar a los diversos 4 politopos.

Un ortosquema de 4 dimensiones es un conjunto de 5 celdas en las que las 10 caras son triángulos rectángulos . (Los 5 vértices forman 5 celdas tetraédricas unidas entre sí por sus caras, con un total de 10 aristas y 10 caras triangulares). Un ortosquema es un símplex irregular que es la envoltura convexa de un árbol en el que todas las aristas son mutuamente perpendiculares. En un ortosquema de 4 dimensiones, el árbol consta de cuatro aristas perpendiculares que conectan los cinco vértices en una trayectoria lineal que realiza tres giros en ángulo recto. Los elementos de un ortosquema también son ortosquemas (así como los elementos de un símplex regular también son símplex regulares). Cada celda tetraédrica de un ortosquema de 4 dimensiones es un ortosquema de 3 dimensiones , y cada cara triangular es un ortosquema de 2 dimensiones (un triángulo rectángulo).

Los ortosquemas son los símplex característicos de los politopos regulares, porque cada politopo regular se genera por reflexiones en las facetas delimitadoras de su ortosquema característico particular. ^[10] Por ejemplo, el caso especial del 4-ortosquema con aristas perpendiculares de igual longitud es el ortosquema característico del 4-cubo (también llamado teseracto o 8-celda ), el análogo 4-dimensional del cubo tridimensional. Si las tres aristas perpendiculares del 4-ortosquema tienen una longitud unitaria, entonces todas sus aristas tienen una longitud √ 1 , √ 2 , √ 3 o √ 4 , precisamente las longitudes de las cuerdas del 4-cubo unitario (las longitudes de las aristas del 4-cubo y sus diversas diagonales). Por lo tanto, este 4-ortosquema encaja dentro del 4-cubo, y el 4-cubo (como todo politopo convexo regular) puede diseccionarse en instancias de su ortosquema característico .

Un 3-ortosquema se ilustra fácilmente, pero un 4-ortosquema es más difícil de visualizar. Un 4-ortosquema es una pirámide tetraédrica con un 3-ortosquema como base. Tiene cuatro aristas más que el 3-ortosquema, uniendo los cuatro vértices de la base a su vértice (el quinto vértice de la celda de 5). Seleccione cualquiera de los 3-ortosquemas de los seis que se muestran en la ilustración del cubo de 3. Observe que toca cuatro de los ocho vértices del cubo, y esos cuatro vértices están unidos por un camino de 3 aristas que realiza dos giros en ángulo recto. Imagina que este 3-ortosquema es la base de un 4-ortosquema, de modo que desde cada uno de esos cuatro vértices, una arista invisible del 4-ortosquema se conecta a un quinto vértice del ápice (que está fuera del 3-cubo y no aparece en absoluto en la ilustración). Aunque las cuatro aristas adicionales llegan todas al mismo vértice del ápice, todas tendrán longitudes diferentes. La primera de ellas, en un extremo del camino ortogonal de 3 aristas, extiende ese camino con una cuarta arista ortogonal √ 1 haciendo un tercer giro de 90 grados y llegando perpendicularmente a la cuarta dimensión hasta el ápice. La segunda de las cuatro aristas adicionales es una diagonal √ 2 de una cara de cubo (no del 3-cubo ilustrado, sino de otro de los ocho 3-cubos del teseracto). La tercera arista adicional es una diagonal √ 3 de un 3-cubo (de nuevo, no el 3-cubo ilustrado original). La cuarta arista adicional (en el otro extremo del camino ortogonal) es un diámetro largo del propio teseracto, de longitud √ 4 . Llega a través del centro exacto del teseracto hasta el vértice antípoda (un vértice del cubo 3 opuesto), que es el ápice. Por lo tanto, la celda 5 característica del cubo 4 tiene cuatro aristas √ 1 , tres aristas √ 2 , dos aristas √ 3 y una arista √ 4 .

El cubo de 4se puede diseccionar en 24 de estos 4-ortosquemas ocho formas diferentes, con seis 4-ortosquemas que rodean cada uno de los cuatro teseractos ortogonales de diámetros largos de √ 4. El 4-cubo también se puede diseccionar en 384 instancias más pequeñas de este mismo 4-ortosquema característico, de una sola manera, por todos sus hiperplanos de simetría a la vez, que lo dividen en 384 4-ortosquemas que se encuentran todos en el centro del 4-cubo.

En términos más generales, cualquier politopo regular puede diseccionarse en g instancias de su ortosquema característico que se encuentran todas en el centro del politopo regular. ^[11] El número g es el orden del politopo, el número de instancias reflejadas de su ortosquema característico que componen el politopo cuando una sola instancia de ortosquema con superficie especular se refleja en sus propias facetas. En términos más generales, los símplex característicos pueden llenar politopos uniformes porque poseen todos los elementos necesarios del politopo. También poseen todos los ángulos necesarios entre elementos (de 90 grados en adelante). Los símplex característicos son los códigos genéticos de los politopos: como una navaja suiza , contienen uno de cada uno de los elementos necesarios para construir el politopo por replicación.

Cada politopo regular, incluido el politopo regular de 5 celdas, tiene su ortosquema característico. Existe un 4-ortosquema que es el politopo regular de 5 celdas característico de 5 celdas . Es una pirámide tetraédrica basada en el tetraedro característico del tetraedro regular . El politopo regular de 5 celdasse puede diseccionar en 120 instancias de este 4-ortoesquema característicosólo de una manera, por todos sus hiperplanos de simetría a la vez, que lo dividen en 120 4-ortoesquemas que se encuentran todos en el centro de la celda regular de 5 celdas.

Características del chip regular de 5 celdas [12]
	borde [13]	arco		diedro [14]
𝒍	${\displaystyle {\sqrt {\tfrac {5}{2}}}\approx 1.581}$	104°30′40″	${\displaystyle \pi -2{\text{𝜂}}}$	75°29′20″	${\displaystyle \pi -2{\text{𝟁}}}$
𝟀	${\displaystyle {\sqrt {\tfrac {1}{10}}}\approx 0.316}$	75°29′20″	${\displaystyle 2{\text{𝜂}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
Yo [a]	${\displaystyle {\sqrt {\tfrac {1}{30}}}\approx 0.183}$	52°15′20″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜂}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
𝟁	${\displaystyle {\sqrt {\tfrac {2}{15}}}\approx 0.103}$	52°15′20″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜂}}}$	60°	${\displaystyle {\tfrac {\pi }{3}}}$
${\displaystyle _{0}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {3}{20}}}\approx 0.387}$	75°29′20″	${\displaystyle 2{\text{𝜂}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{1}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {1}{20}}}\approx 0.224}$	52°15′20″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜂}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{2}R^{3}/l}$	${\displaystyle {\sqrt {\tfrac {1}{60}}}\approx 0.129}$	52°15′20″	${\displaystyle {\tfrac {\pi }{2}}-{\text{𝜂}}}$	90°	${\displaystyle {\tfrac {\pi }{2}}}$
${\displaystyle _{0}R^{4}/l}$	${\displaystyle {\sqrt {1}}=1.0}$
${\displaystyle _{1}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {3}{8}}}\approx 0.612}$
${\displaystyle _{2}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {1}{6}}}\approx 0.408}$
${\displaystyle _{3}R^{4}/l}$	${\displaystyle {\sqrt {\tfrac {1}{16}}}=0.25}$
${\displaystyle {\text{𝜼}}}$		37°44′40″	${\displaystyle {\tfrac {{\text{arc sec }}4}{2}}}$

El tetraedro característico de 5 celdas (4-ortosquema) del tetraedro regular de 5 celdas tiene cuatro aristas más que su tetraedro característico de base (3-ortosquema), que unen los cuatro vértices de la base a su vértice (el quinto vértice del 4-ortosquema, en el centro del tetraedro regular de 5 celdas). Las cuatro aristas de cada 4-ortosquema que se encuentran en el centro de un tetrapolitopo regular tienen una longitud desigual, porque son los cuatro radios característicos del tetrapolitopo regular: un radio de vértice, un radio de centro de arista, un radio de centro de cara y un radio de centro de celda. Si la celda regular de 5 tiene un radio unitario y una longitud de arista , sus diez aristas características de la celda de 5 tienen longitudes , , alrededor de su cara exterior de triángulo rectángulo (las aristas opuestas a los ángulos característicos 𝟀, 𝝉, 𝟁), ^[a] más , , (las otras tres aristas de la faceta exterior del ortosquema de 3 haces del tetraedro característico, que son los radios característicos del tetraedro regular), más , , , (aristas que son los radios característicos de la celda regular de 5). La ruta de 4 aristas a lo largo de las aristas ortogonales del ortosquema es , , , , primero desde un vértice regular de la celda de 5 hasta un centro de la arista regular de la celda de 5, luego girando 90° hasta el centro de la cara de la celda de 5, luego girando 90° hasta el centro de la celda tetraédrica regular de la celda de 5, luego girando 90° hasta el centro de la celda regular de 5.${\displaystyle {\sqrt {\tfrac {5}{2}}}}$${\displaystyle {\sqrt {\tfrac {1}{10}}}}$${\displaystyle {\sqrt {\tfrac {1}{30}}}}$${\displaystyle {\sqrt {\tfrac {2}{15}}}}$${\displaystyle {\sqrt {\tfrac {3}{20}}}}$${\displaystyle {\sqrt {\tfrac {1}{20}}}}$${\displaystyle {\sqrt {\tfrac {1}{60}}}}$${\displaystyle {\sqrt {1}}}$${\displaystyle {\sqrt {\tfrac {3}{8}}}}$${\displaystyle {\sqrt {\tfrac {1}{6}}}}$${\displaystyle {\sqrt {\tfrac {1}{16}}}}$${\displaystyle {\sqrt {\tfrac {1}{30}}}}$${\displaystyle {\sqrt {\tfrac {2}{15}}}}$${\displaystyle {\sqrt {\tfrac {1}{60}}}}$${\displaystyle {\sqrt {\tfrac {1}{16}}}}$

Existen muchas formas de simetría inferior de 5 celdas, incluidas las que se encuentran como figuras de vértice de politopo uniforme :

Simetría	[3,3,3] Orden 120	[3,3,1] Orden 24	[3,2,1] Orden 12	[3,1,1] Orden 6	~[5,2] + Orden 10
Nombre	Regular de 5 celdas	Pirámide tetraédrica		Pirámide piramidal triangular
Colapso	{3,3,3}	{3,3}∨( )	{3}∨{ }	{3}∨( )∨( )
Ejemplo de figura de vértice	5-símplex	5-símplex truncado	5-símplex bitruncado	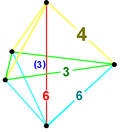5-símplex cantitruncado	Panal de abeja 4-símplex omnitruncado

La pirámide tetraédrica es un caso especial de pirámide poliédrica de cinco celdas , construida como una base tetraédrica regular en un hiperplano de tres espacios y un punto de vértice sobre el hiperplano. Los cuatro lados de la pirámide están formados por celdas piramidales triangulares .

Muchos 5-politopos uniformes tienen figuras de vértice de pirámides tetraédricas con símbolos de Schläfli ( )∨{3,3}.

Simetría [3,3,1], orden 24

Diagrama de Schlegel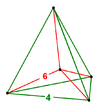
Nombre Coxeter	{ }×{3,3,3}	{ }×{4,3,3}	{ }×{5,3,3}	t{3,3,3,3}	t{4,3,3,3}	t{3,4,3,3}

Otros politopos 5 uniformes tienen figuras de vértices de 5 celdas irregulares. La simetría de una figura de vértice de un politopo uniforme se representa eliminando los nodos en anillo del diagrama de Coxeter.

Simetría	[3,2,1], orden 12		[3,1,1], orden 6		[2 + ,4,1], orden 8	[2,1,1], orden 4
Colapso	{3}∨{ }		{3}∨( )∨( )		{ }∨{ }∨( )
Diagrama de Schlegel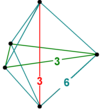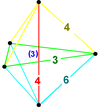
Nombre Coxeter	t12α5​​​	t12γ5​​​	t 012 a 5	t012 γ5​​	t123α5​​​	t123γ5​​​

Simetría	[2,1,1], orden 2			[2 + ,1,1], orden 2	[ ] + , orden 1
Colapso	{ }∨( )∨( )∨( )			( )∨( )∨( )∨( )∨( )
Diagrama de Schlegel
Nombre Coxeter	t0123 α5​​	t0123 γ5​​	t0123β5​​​	t01234 a 5​	t01234 y 5​

Un 5-cell puede construirse como una hélice de Boerdijk-Coxeter de cinco tetraedros encadenados, plegados en un anillo de 4 dimensiones. ^[15] Las 10 caras de los triángulos pueden verse en una red 2D dentro de un mosaico triangular , con 6 triángulos alrededor de cada vértice, aunque el plegado en 4 dimensiones hace que los bordes coincidan. Los bordes morados forman un pentágono regular que es el polígono de Petrie del 5-cell. Los bordes azules conectan cada segundo vértice, formando un pentagrama que es el polígono de Clifford del 5-cell. Los bordes azules del pentagrama son las cuerdas de la isoclina del 5-cell , la trayectoria de rotación circular que toman sus vértices durante una rotación isoclínica , también conocida como desplazamiento de Clifford .

Cuando se pliega una red de cinco tetraedros en un espacio de cuatro dimensiones de modo que cada tetraedro está unido por una cara a los otros cuatro, las cinco celdas resultantes tienen un total de cinco vértices, diez aristas y diez caras. Cuatro aristas se unen en cada vértice y tres celdas tetraédricas se unen en cada arista. Esto hace que el tetraedro de seis caras sea su celda . ^[6]

El conjunto más simple de coordenadas cartesianas es: (2,0,0,0), (0,2,0,0), (0,0,2,0), (0,0,0,2), (𝜙,𝜙,𝜙,𝜙), con una longitud de arista de 2 √ 2 , donde 𝜙 es la proporción áurea . ^[16] Si bien estas coordenadas no están centradas en el origen, al restar de cada una se traslada el circuncentro del 4-politopo al origen con radio , con las siguientes coordenadas:${\displaystyle (1,1,1,1)/(2-{\tfrac {1}{\phi }})}$${\displaystyle 2(\phi -1/(2-{\tfrac {1}{\phi }}))={\sqrt {\tfrac {16}{5}}}\approx 1.7888}$

${\displaystyle \left({\tfrac {2}{\phi }}-3,1,1,1\right)/({\tfrac {1}{\phi }}-2)}$

${\displaystyle \left(1,{\tfrac {2}{\phi }}-3,1,1\right)/({\tfrac {1}{\phi }}-2)}$

${\displaystyle \left(1,1,{\tfrac {2}{\phi }}-3,1\right)/({\tfrac {1}{\phi }}-2)}$

${\displaystyle \left(1,1,1,{\tfrac {2}{\phi }}-3\right)/({\tfrac {1}{\phi }}-2)}$

${\displaystyle \left({\tfrac {2}{\phi }},{\tfrac {2}{\phi }},{\tfrac {2}{\phi }},{\tfrac {2}{\phi }}\right)/({\tfrac {1}{\phi }}-2)}$

El siguiente conjunto de coordenadas centradas en el origen con el mismo radio y longitud de arista que el anterior puede verse como una hiperpirámide con una base tetraédrica regular en el espacio tridimensional:

${\displaystyle \left(1,1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(1,-1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,1,-1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(-1,-1,1,{\frac {-1}{\sqrt {5}}}\right)}$

${\displaystyle \left(0,0,0,{\frac {4}{\sqrt {5}}}\right)}$

Al escalar estas o las coordenadas anteriores, se obtienen 5 celdas regulares centradas en el origen y con radio unitario y longitudes de aristas . La hiperpirámide tiene las siguientes coordenadas:${\displaystyle {\tfrac {\sqrt {5}}{4}}}$${\displaystyle {\sqrt {\tfrac {5}{2}}}}$

${\displaystyle \left({\sqrt {5}},{\sqrt {5}},{\sqrt {5}},-1\right)/4}$

${\displaystyle \left({\sqrt {5}},-{\sqrt {5}},-{\sqrt {5}},-1\right)/4}$

${\displaystyle \left(-{\sqrt {5}},{\sqrt {5}},-{\sqrt {5}},-1\right)/4}$

${\displaystyle \left(-{\sqrt {5}},-{\sqrt {5}},{\sqrt {5}},-1\right)/4}$

${\displaystyle \left(0,0,0,1\right)}$

Las coordenadas de los vértices de otro sistema regular de 5 celdas centrado en el origen con longitud de arista 2 y radio son:${\displaystyle {\sqrt {\tfrac {8}{5}}}\approx 1.265}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {1}{\sqrt {3}}},\ \pm 1\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ {\frac {1}{\sqrt {6}}},\ {\frac {-2}{\sqrt {3}}},\ 0\right)}$

${\displaystyle \left({\frac {1}{\sqrt {10}}},\ -{\sqrt {\frac {3}{2}}},\ 0,\ 0\right)}$

${\displaystyle \left(-2{\sqrt {\frac {2}{5}}},\ 0,\ 0,\ 0\right)}$

Al escalarlos por unidad de radio y longitud de borde se obtiene:${\displaystyle {\sqrt {\tfrac {5}{8}}}}$${\displaystyle {\sqrt {\tfrac {5}{2}}}}$

${\displaystyle \left({\sqrt {3}},{\sqrt {5}},{\sqrt {10}},\pm {\sqrt {30}}\right)/(4{\sqrt {3}})}$

${\displaystyle \left({\sqrt {3}},{\sqrt {5}},-{\sqrt {40}},0\right)/(4{\sqrt {3}})}$

${\displaystyle \left({\sqrt {3}},-{\sqrt {45}},0,0\right)/(4{\sqrt {3}})}$

${\displaystyle \left(-1,0,0,0\right)}$

Los vértices de un 4-símplex (con arista √ 2 y radio 1) se pueden construir de forma más sencilla en un hiperplano en el 5-espacio, como permutaciones (distintas) de (0,0,0,0,1) o (0,1,1,1,1); en estas posiciones es una faceta del 5-ortoplex o del penteracto rectificado , respectivamente .

El compuesto de dos celdas de 5 en configuraciones duales se puede ver en esta proyección del plano de Coxeter A5 , con vértices y aristas de 5 celdas rojas y azules. Este compuesto tiene simetría [[3,3,3]], orden 240. La intersección de estas dos celdas de 5 es un bitruncado uniforme de 5 celdas .=∩.

Este compuesto puede verse como el análogo 4D del hexagrama 2D { ⁠6/2} y el compuesto 3D de dos tetraedros .

El pentacorone (de 5 células) es el más simple de los 9 policoros uniformes construidos a partir del grupo de Coxeter [3,3,3] .

Colapso	{3,3,3}	t{3,3,3}	r{3,3,3}	rr{3,3,3}	2t{3,3,3}	tr{3,3,3}	t0,3 { 3,3,3 }	t0,1,3 { 3,3,3}	t0,1,2,3 { 3,3,3 }
Coxeter
Schlegel

1 k2 figuras en n dimensiones
Espacio	Finito						Euclidiano	Hiperbólico
norte	3	4	5	6	7	8	9	10
Grupo Coxeter	E3 = Un2Un1​​​	E4 = A4​	E5 = D5​	E6​	E7​	E8​	E9 = = E8 +​${\displaystyle {\tilde {E}}_{8}}$	E10 = = E8 ++​${\displaystyle {\bar {T}}_{8}}$
Diagrama de Coxeter
Simetría (orden)	[3 −1,2,1 ]	[3 0,2,1 ]	[3 1,2,1 ]	[[3 2,2,1 ]]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Orden	12	120	1.920	103.680	2.903.040	696.729.600	∞
Gráfico							-	-
Nombre	1 −1,2	102	1 12	1 22	1 32	1 42	1 52	1 62

2 k 1 cifras en n dimensiones
Espacio	Finito						Euclidiano	Hiperbólico
norte	3	4	5	6	7	8	9	10
Grupo Coxeter	E3 = Un2Un1​​​	E4 = A4​	E5 = D5​	E6​	E7​	E8​	E9 = = E8 +​${\displaystyle {\tilde {E}}_{8}}$	E10 = = E8 ++​${\displaystyle {\bar {T}}_{8}}$
Diagrama de Coxeter
Simetría	[3 −1,2,1 ]	[3 0,2,1 ]	[[3 1,2,1 ]]	[3 2,2,1 ]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Orden	12	120	384	51.840	2.903.040	696.729.600	∞
Gráfico							-	-
Nombre	2 −1,1	2 01	2 11	2 21	2 31	2 41	2 51	2 61

Está en la secuencia {p,3,3} de policoras regulares con figura de vértice tetraédrico : el teseracto {4,3,3} y las 120 celdas {5,3,3} del 4-espacio euclidiano, y el panal de teselación hexagonal {6,3,3} del espacio hiperbólico.

{p,3,3} politopos
Espacio		S 3			H3​
Forma		Finito			Paracompacto	No compacto
Nombre		{3,3,3}	{4,3,3}	{5,3,3}	{6,3,3}	{7,3,3}	{8,3,3}	... {∞,3,3}
Imagen
Células {p,3}		{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Es uno de los tres politopos 4 regulares {3,3,p} con celdas tetraédricas, junto con el {3,3,4} de 16 celdas y el {3,3,5} de 600 celdas . El panal tetraédrico de orden 6 {3,3,6} del espacio hiperbólico también tiene celdas tetraédricas.

politopos {3,3,p}
Espacio	S 3			H3​
Forma	Finito			Paracompacto	No compacto
Nombre	{3,3,3}	{3,3,4}	{3,3,5}	{3,3,6}	{3,3,7}	{3,3,8}	... {3,3,∞}
Imagen
Figura de vértice	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

Es autodual como el {3,4,3} de 24 celdas , y tiene un símbolo Schläfli palindrómico {3,p,3} .

{3, p ,3} politopos
Espacio	S 3		H3​
Forma	Finito		Compacto	Paracompacto	No compacto
{3, pág . 3}	{3,3,3}	{3,4,3}	{3,5,3}	{3,6,3}	{3,7,3}	{3,8,3}	... {3,∞,3}
Imagen
Células	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}
Figura de vértice	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

{p,3,p} panales regulares
Espacio	S 3	E 3 euclidiana	H3​
Forma	Finito	Afín	Compacto	Paracompacto	No compacto
Nombre	{3,3,3}	{4,3,4}	{5,3,5}	{6,3,6}	{7,3,7}	{8,3,8}	... {∞,3,∞}
Imagen
Células	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}
Figura de vértice	{3,3}	{3,4}	{3,5}	{3,6}	{3,7}	{3,8}	{3,∞}

• Akiyama, Jin; Hitotumatu, pecado; Sato, Ikuro (2012). "Determinación del número de elementos de los politopos regulares". Geometriae Dedicata . 159 : 89–97. doi :10.1007/s10711-011-9647-3.
• Diudea, MV (2018). Cúmulos poliédricos de múltiples capas. Materiales de carbono: química y física. Vol. 10. Springer . doi :10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
• Ghyka, Matila (1977). La geometría del arte y la vida. Dover Publications . ISBN 978-0-486-23542-4.
• Johnson, NW (2018). "Grupos de simetría finita, 11.5 Grupos esféricos de Coxeter". Geometrías y transformaciones . Cambridge University Press. ISBN 978-1-107-10340-5.
• Miyazaki, K.; Ishii, M. (2021). "Simetría en la proyección de policoros regulares de cuatro dimensiones". En Darvas, György (ed.). Simetrías complejas. doi :10.1007/978-3-030-88059-0. ISBN: 978-3-030-88059-0 . 978-3-030-88059-0.
• T. Gosset : Sobre las figuras regulares y semirregulares en el espacio de n dimensiones , Messenger of Mathematics, Macmillan, 1900
• HSM Coxeter :
  • Coxeter, HSM (1973). Politopos regulares (3.ª ed.). Nueva York: Dover.
    • p. 120, §7.2. ver ilustración Fig 7.2 A
    • p. 296, Tabla I (iii): Politopos regulares, tres politopos regulares en n-dimensiones (n≥5)
  • Coxeter, HSM (1991), Politopos complejos regulares (2.ª ed.), Cambridge: Cambridge University Press
  • Caleidoscopios: escritos selectos de HSM Coxeter, editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
    • (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
    • (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
• Kim, Heuna; Rote, G. (2016). "Prueba de congruencia de conjuntos de puntos en 4 dimensiones". arXiv : 1603.07269 [cs.CG].
• John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 (Capítulo 26, págs. 409: Hemicubos: 1 _n1 ) 
• Manuscrito de politopos uniformes de Norman Johnson (1991)
  • NW Johnson: La teoría de los politopos uniformes y los panales de abejas , Ph.D. (1966)
• Banchoff, Thomas F. (2013). "Descomposiciones en toro de politopos regulares en el espacio 4". En Senechal, Marjorie (ed.). Shaping Space . Springer Nueva York. págs. 257–266. doi :10.1007/978-0-387-92714-5_20. ISBN 978-0-387-92713-8.

• Weisstein, Eric W. "Pentatopo". MathWorld .
• Klitzing, Richard. "Polítopos uniformes 4D (policoros) x3o3o3o - pluma".
• Der 5-Zeller (5 celdas) Politopos regulares de Marco Möller en R ⁴ (alemán)
• Jonathan Bowers, Polychora regular
• Subprogramas Java3D
• pirocoron