Rectificado de 24 celdas

Rectificado de 24 celdas
Diagrama de Schlegel 8 de 24 celdas cuboctaédricas mostradas
Tipo	Politopo 4 uniforme
Símbolos de Schläfli	r{3,4,3} = rr{3,3,4} = r{3 1,1,1 } =${\displaystyle \left\{{\begin{array}{l}3\\4,3\end{array}}\right\}}$ ${\displaystyle r\left\{{\begin{array}{l}3\\3,4\end{array}}\right\}}$ ${\displaystyle r\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}}$
Diagramas de Coxeter	o
Células	48	24 3.4.3.4 24 4.4.4
Caras	240	96 {3} 144 {4}
Bordes	288
Vértices	96
Figura de vértice	Prisma triangular
Grupos de simetría	F 4 [3,4,3], orden 1152 B 4 [3,3,4], orden 384 D 4 [3 1,1,1 ], orden 192
Propiedades	convexo , transitivo en los bordes
Índice uniforme	22 23 24

En geometría , el icositetracoron rectificado de 24 celdas o icositetracoron rectificado es un politopo uniforme de 4 dimensiones (o 4-politopo uniforme ), que está limitado por 48 celdas : 24 cubos y 24 cuboctaedros . Se puede obtener por rectificación del politopo de 24 celdas, reduciendo sus celdas octaédricas a cubos y cuboctaedros. ^[1]

EL Elte lo identificó en 1912 como un politopo semirregular, etiquetándolo como tC ₂₄ .

También puede considerarse un cantelado de 16 celdas con las simetrías inferiores B ₄ = [3,3,4]. B ₄ daría lugar a una bicoloración de las celdas cuboctaédricas en 8 y 16 cada una. También se denomina demiteseracto runcicantelado en una simetría D ₄ , lo que da 3 colores de celdas, 8 para cada una.

El sistema de 24 celdas rectificado se puede derivar del sistema de 24 celdas mediante el proceso de rectificación : el sistema de 24 celdas se trunca en los puntos medios. Los vértices se convierten en cubos , mientras que los octaedros se convierten en cuboctaedros .

Una celda rectificada de 24 que tiene una longitud de arista de √ 2 tiene vértices dados por todas las permutaciones y permutaciones de signo de las siguientes coordenadas cartesianas :

(0,1,1,2) [4!/2!×2 ³ = 96 vértices]

La configuración dual con longitud de arista 2 tiene todas las permutaciones de coordenadas y signos de:

(0,2,2,2) [4×2 ³ = 32 vértices]

(1,1,1,3) [4×2 ⁴ = 64 vértices]

proyecciones ortográficas

Avión Coxeter	F4​
Gráfico
Simetría diedral	[12]
Avión Coxeter	B3 / A2 ( a )	B3 / A2 ( b )
Gráfico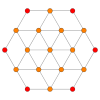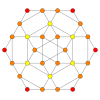
Simetría diedral	[6]	[6]
Avión Coxeter	B4​	B2 / A3​
Gráfico
Simetría diedral	[8]	[4]

Proyección estereográfica
Centro de proyección estereográfica con 96 caras triangulares de color azul

Hay tres construcciones de simetría diferentes de este politopo. La construcción más baja se puede duplicar agregando un espejo que mapee los nodos bifurcados entre sí. Se puede mapear hasta la simetría agregando dos espejos que mapeen los tres nodos finales juntos.${\displaystyle {D}_{4}}$${\displaystyle {C}_{4}}$${\displaystyle {D}_{4}}$${\displaystyle {F}_{4}}$

La figura del vértice es un prisma triangular que contiene dos cubos y tres cuboctaedros. Las tres simetrías se pueden ver con 3 cuboctaedros de colores en la construcción más baja, y dos colores (ratio 1:2) en , y todos los cuboctaedros idénticos en .${\displaystyle {D}_{4}}$${\displaystyle {C}_{4}}$${\displaystyle {F}_{4}}$

Grupo Coxeter	${\displaystyle {F}_{4}}$= [3,4,3]	${\displaystyle {C}_{4}}$= [4,3,3]	${\displaystyle {D}_{4}}$= [3,3 1,1 ]
Orden	1152	384	192
Grupo de simetría completa	[3,4,3]	[4,3,3]	<[3,3 1,1 ]> = [4,3,3] [3[3 1,1,1 ]] = [3,4,3]
Diagrama de Coxeter
Facetas	3: 2:	2,2: 2:	1,1,1: 2:
Figura de vértice

• Rectificado de 24 celdas, Cantelado de 16 celdas ( Norman Johnson )
• Icositetracoron rectificado (acrónimo rico) (George Olshevsky, Jonathan Bowers)
  • Hexadecacoron cantelado
• Disicositetracoron
• Amboicositetrachoron ( Neil Sloane y John Horton Conway )

La envoltura convexa del policoro rectificado de 24 celdas y su dual (suponiendo que son congruentes) es un policoro no uniforme compuesto por 192 celdas: 48 cubos , 144 antiprismas cuadrados y 192 vértices. Su figura de vértice es un bitruco triangular .

D 4 policora uniforme
{3,3 1,1 } h{4,3,3}	2r{3,3 1,1 } h3 {4,3,3 }	t{3,3 1,1 } h2 {4,3,3 }	2t{3,3 1,1 } h2,3 { 4,3,3}	r{3,3 1,1 } {3 1,1,1 }={3,4,3}	rr{3,31,1} r{3 1,1,1 }=r{3,4,3}	tr{3,3 1,1 } t{3 1,1,1 }=t{3,4,3}	sr{3,3 1,1 } s{3 1,1,1 }=s{3,4,3}

Politopos de la familia de 24 células
Nombre	24 celdas	24 celdas truncadas	snub de 24 celdas	rectificado de 24 celdas	cantelado de 24 celdas	bitruncado de 24 celdas	cantitruncado de 24 celdas	Runcinated de 24 celdas	Runcitruncado de 24 celdas	omnitruncado de 24 celdas
Símbolo de Schläfli	{3,4,3}	t0,1 {3,4,3} t { 3,4,3}	s{3,4,3}	t1 { 3,4,3 } r{3,4,3}	t 0,2 {3,4,3} rr{3,4,3}	t1,2 {3,4,3} 2t {3,4,3}	t 0,1,2 {3,4,3} tr{3,4,3}	t0,3 { 3,4,3}	t0,1,3 { 3,4,3}	t0,1,2,3 { 3,4,3 }
Diagrama de Coxeter
Diagrama de Schlegel
F4​
B4​
B3 (a )
B3 (b )
B2​

La celda rectificada de 24 celdas también se puede derivar como una celda cantelada de 16 celdas :

Politopos de simetría B4
Nombre	teseracto	teseracto rectificado	teseracto truncado	teseracto cantelado	teseracto runcinado	teseracto bitruncado	teseracto truncado	teseracto runcitruncado	teseracto omnitruncado
Diagrama de Coxeter		=				=
Símbolo de Schläfli	{4,3,3}	t1 { 4,3,3 } r{4,3,3}	t0,1 {4,3,3} t { 4,3,3}	t 0,2 {4,3,3} rr{4,3,3}	t0,3 { 4,3,3}	t1,2 {4,3,3} 2t {4,3,3}	t 0,1,2 {4,3,3} tr{4,3,3}	t0,1,3 { 4,3,3}	t0,1,2,3 { 4,3,3}
Diagrama de Schlegel
B4​
Nombre	16 celdas	rectificado de 16 celdas	16 celdas truncadas	cantelado de 16 celdas	Runcinated de 16 celdas	bitruncado de 16 celdas	cantitruncado de 16 celdas	Runcitruncado de 16 celdas	omnitruncado de 16 celdas
Diagrama de Coxeter	=	=	=	=		=	=
Símbolo de Schläfli	{3,3,4}	t1 { 3,3,4 } r{3,3,4}	t0,1 {3,3,4} t { 3,3,4}	t 0,2 {3,3,4} rr{3,3,4}	t0,3 { 3,3,4}	t1,2 {3,3,4} 2t {3,3,4}	t 0,1,2 {3,3,4} tr{3,3,4}	t0,1,3 { 3,3,4}	t0,1,2,3 { 3,3,4}
Diagrama de Schlegel
B4​

• T. Gosset : Sobre las figuras regulares y semirregulares en el espacio de n dimensiones , Messenger of Mathematics, Macmillan, 1900
• Coxeter, HSM (1973) [1948]. Politopos regulares (3.ª ed.). Nueva York: Dover.
• John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 (Capítulo 26, págs. 409: Hemicubos: 1 _n1 ) 
• Manuscrito de politopos uniformes de Norman Johnson (1991)
  • NW Johnson: La teoría de los politopos uniformes y los panales de abejas , Ph.D. (1966)
• 2. Polícora uniforme convexa basada en el teseracto (8 celdas) y el hexadecacoron (16 celdas) - Modelo 23, George Olshevsky.
  • 3. Polícora uniforme convexa basada en el icositetracoron (24 células) - Modelo 23, George Olshevsky.
  • 7. Policora uniforme derivada del tetraedro glomérico B4 - Modelo 23, George Olshevsky.
• Klitzing, Richard. "Polítopos uniformes 4D (polichora) o3x4o3o - rico".