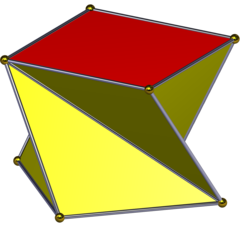
Antiprisma cuadrado
| Antiprisma cuadrado uniforme | |
|---|---|
 | |
| Tipo | Poliedro prismático uniforme |
| Elementos | F = 10, E = 16 V = 8 (χ = 2) |
| Caras por lados | 8{3}+2{4} |
| Símbolo de Schläfli | s{2,8} sr{2,4} |
| Símbolo de Wythoff | | 2 2 4 |
| Diagrama de Coxeter |           |
| Grupo de simetría | D 4d , [2 + ,8], (2*4), orden 16 |
| Grupo de rotación | D 4 , [4,2] + , (442), orden 8 |
| Referencias | U 77(b) |
| Dual | Trapezoedro tetragonal |
| Propiedades | convexo |
 Figura de vértice 3.3.3.4 | |

En geometría , el antiprisma cuadrado es el segundo de una familia infinita de antiprismas formados por una secuencia de lados pares de triángulos cerrados por dos tapas poligonales . También se lo conoce como anticubo . [1]
Si todas sus caras son regulares se trata de un poliedro semirregular o poliedro uniforme .
Una variante D4 - simétrica no uniforme es la celda del antiprismático cuadrado noble de 72 celdas.
Puntos en una esfera
Cuando se distribuyen ocho puntos sobre la superficie de una esfera con el objetivo de maximizar en algún sentido la distancia entre ellos, la forma resultante corresponde a un antiprisma cuadrado en lugar de a un cubo . Los métodos específicos de distribución de los puntos incluyen, por ejemplo, el problema de Thomson (minimizar la suma de todos los recíprocos de las distancias entre puntos), maximizar la distancia de cada punto al punto más cercano o minimizar la suma de todos los recíprocos de los cuadrados de las distancias entre puntos.
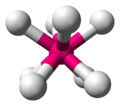
Moléculas con geometría antiprismática cuadrada
Según la teoría VSEPR de geometría molecular en química , que se basa en el principio general de maximizar las distancias entre puntos, un antiprisma cuadrado es la geometría preferida cuando ocho pares de electrones rodean un átomo central . Una molécula con esta geometría es el ion octafluoroxenato(VI) ( XeF2−
8) en la sal octafluoroxenato de nitrosonio (VI) ; sin embargo, la molécula se distorsiona alejándose del antiprisma cuadrado idealizado. [2] Muy pocos iones son cúbicos porque tal forma causaría una gran repulsión entre ligandos ; PaF3−
8es uno de los pocos ejemplos. [3]
Además, el elemento azufre forma moléculas octatómicas de S 8 como su alótropo más estable . La molécula de S 8 tiene una estructura basada en el antiprisma cuadrado, en el que los ocho átomos ocupan los ocho vértices del antiprisma, y las ocho aristas triángulo-triángulo del antiprisma corresponden a enlaces covalentes simples entre átomos de azufre.
En arquitectura
El bloque principal del One World Trade Center (en el lugar donde se encontraba el antiguo World Trade Center, destruido el 11 de septiembre de 2001 ) tiene la forma de un antiprisma cuadrado extremadamente alto y cónico. No es un antiprisma verdadero debido a su forma cónica: el cuadrado superior tiene la mitad del área del inferior.
Poliedros topológicamente idénticos
Prisma torcido
Se puede construir un prisma torcido (en sentido horario o antihorario) con la misma disposición de vértices . Se puede ver como la forma convexa con 4 tetraedros excavados alrededor de los lados. Sin embargo, después de esto ya no se puede triangular en tetraedros sin agregar nuevos vértices. Tiene la mitad de la simetría de la solución uniforme: D 4 orden 4. [4] [5]
Antiprisma cruzado
Un antiprisma cuadrado cruzado es un poliedro estrellado , topológicamente idéntico al antiprisma cuadrado con la misma disposición de vértices , pero no puede hacerse uniforme; los lados son triángulos isósceles . Su configuración de vértices es 3.3/2.3.4, con un triángulo retrógrado. Tiene simetría d 4d , orden 8.
Poliedros relacionados
Poliedros derivados
La pirámide cuadrada giroelongada es un sólido de Johnson (en concreto, J 10 ) construido aumentando una pirámide cuadrada . De forma similar, la bipirámide cuadrada giroelongada ( J 17 ) es un deltaedro (un poliedro cuyas caras son todos triángulos equiláteros ) construido reemplazando ambos cuadrados de un antiprisma cuadrado por una pirámide cuadrada.
El disfenoide romo ( J 84 ) es otro deltaedro, construido reemplazando los dos cuadrados de un antiprisma cuadrado por pares de triángulos equiláteros. El antiprisma cuadrado romo ( J 85 ) puede verse como un antiprisma cuadrado con una cadena de triángulos equiláteros insertados alrededor del medio. La esfenocorona ( J 86 ) y la esfenomegacorona ( J 88 ) son otros sólidos de Johnson que, como el antiprisma cuadrado, consisten en dos cuadrados y un número par de triángulos equiláteros.
El antiprisma cuadrado se puede truncar y alternar para formar un antiprisma chato :
| Antiprisma | t truncada | Alt. alternado |
|---|---|---|
 s{2,8}      |  ts{2,8} |  ss{2,8} |
Mutación de simetría
Como antiprisma , el antiprisma cuadrado pertenece a una familia de poliedros que incluye el octaedro (que puede verse como un antiprisma con un triángulo en la parte superior), el antiprisma pentagonal , el antiprisma hexagonal y el antiprisma octogonal .
| Nombre del antiprisma | Antiprisma digonal | Antiprisma triangular (trigonal) | Antiprisma cuadrado (tetragonal) | Antiprisma pentagonal | Antiprisma hexagonal | Antiprisma heptagonal | ... | Antiprisma apeirogonal |
|---|---|---|---|---|---|---|---|---|
| Imagen de poliedro |  |  |  |  |  |  | ... | |
| Imagen de mosaico esférico |  |  |  |  |  |  | Imagen de mosaico plano |  |
| Configuración de vértice. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | ... | ∞.3.3.3 |
El antiprisma cuadrado es el primero de una serie de poliedros romos y teselaciones con vértice en la figura 3.3.4.3.n.
| 4 n 2 mutaciones de simetría de teselaciones snub: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simetría 4 n 2 | Esférico | Euclidiano | Hiperbólica compacta | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
Figuras desairadas |  |  |  |  |  |  |  |  |
| Configuración. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
Figuras de giroscopio |  |  |  |  | ||||
| Configuración. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
Ejemplos
- Edificio One World Trade Center
- Antiprisma cuadrado
(en Matemateca Ime-USP) - Antiprisma cuadrado romo
(en Matemateca IME-USP)
Véase también
Notas
- ^ Holleman-Wiberg. Química inorgánica , Academic Press, Italia, pág. 299. ISBN 0-12-352651-5 .
- ^ Peterson, W.; Holloway, H.; Coyle, A.; Williams, M. (septiembre de 1971). "Coordinación antiprismática sobre el xenón: la estructura del octafluoroxenato de nitrosonio (VI)". Science . 173 (4003): 1238–1239. Bibcode :1971Sci...173.1238P. doi :10.1126/science.173.4003.1238. ISSN 0036-8075. PMID 17775218. S2CID 22384146.
- ^ Greenwood, Norman N. ; Earnshaw, Alan (1997). Química de los elementos (2.ª ed.). Butterworth-Heinemann . p. 1275. ISBN 978-0-08-037941-8.
- ^ Los hechos en el expediente: Manual de geometría, Catherine A. Gorini, 2003, ISBN 0-8160-4875-4 , p.172
- ^ "Imágenes de prismas retorcidos".
Enlaces externos
- Weisstein, Eric W. "Antiprisma". MathWorld .
- Modelo interactivo del antiprisma cuadrado
- Poliedros de realidad virtual www.georgehart.com: La enciclopedia de poliedros
- Modelo VRML
- poliedronismo A4