10-símplex

Endecaxenón regular (10-simplex)
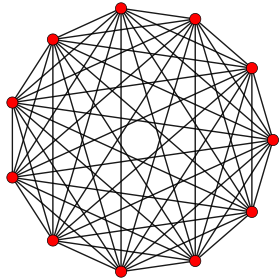Proyección ortogonal dentro del polígono de Petrie
Tipo	Politopo 10 regular
Familia	símplex
Símbolo de Schläfli	{3,3,3,3,3,3,3,3,3}
Diagrama de Coxeter-Dynkin
9 caras	11 9-símplex
8 caras	55 8-símplex
7 caras	165 7-símplex
6 caras	330 6-símplex
5 caras	462 5-símplex
4 caras	462 5 celdas
Células	330 tetraedro
Caras	165 triángulo
Bordes	55
Vértices	11
Figura de vértice	9-símplex
Polígono de Petrie	endecágono
Grupo Coxeter	Un 10 [3,3,3,3,3,3,3,3,3]
Dual	Auto-dual
Propiedades	convexo

En geometría , un 10- símplex es un 10-politopo regular autodual . Tiene 11 vértices , 55 aristas , 165 caras triangulares, 330 celdas tetraédricas , 462 5-celdas de 4 caras, 462 5-símplex de 5 caras, 330 6-símplex de 6 caras, 165 7-símplex de 7 caras, 55 8-símplex de 8 caras y 11 9-símplex de 9 caras. Su ángulo diedro es cos ⁻¹ (1/10), o aproximadamente 84,26°.

También se le puede llamar endecaxeno o endeca-10-topo , ya que es un politopo de 11 facetas en 10 dimensiones. El nombre endecaxeno se deriva de hendeca , que significa 11 facetas en griego , y -xenn (variación de ennea, que significa nueve), que tiene facetas de 9 dimensiones, y -on .

Las coordenadas cartesianas de los vértices de un 10-símplex regular centrado en el origen que tiene una longitud de arista de 2 son:

${\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ {\sqrt {1/3}},\ \pm 1\right)}$

${\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ {\sqrt {1/6}},\ -2{\sqrt {1/3}},\ 0\right)}$

${\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ {\sqrt {1/10}},\ -{\sqrt {3/2}},\ 0,\ 0\right)}$

${\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ {\sqrt {1/15}},\ -2{\sqrt {2/5}},\ 0,\ 0,\ 0\right)}$

${\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ {\sqrt {1/21}},\ -{\sqrt {5/3}},\ 0,\ 0,\ 0,\ 0\right)}$

${\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ {\sqrt {1/28}},\ -{\sqrt {12/7}},\ 0,\ 0,\ 0,\ 0,\ 0\right)}$

${\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ 1/6,\ -{\sqrt {7/4}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}$

${\displaystyle \left({\sqrt {1/55}},\ {\sqrt {1/45}},\ -4/3,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}$

${\displaystyle \left({\sqrt {1/55}},\ -3{\sqrt {1/5}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}$

${\displaystyle \left(-{\sqrt {20/11}},\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0,\ 0\right)}$

En términos más simples, los vértices del 10-símplex se pueden posicionar en el 11-espacio como permutaciones de (0,0,0,0,0,0,0,0,0,0,1). Esta construcción se basa en facetas del 11-ortoplex .

proyecciones ortográficas

Un avión de Coxeter	Un 10	Un 9	Un 8
Gráfico
Simetría diedral	[11]	[10]	[9]
Un avión de Coxeter	Un 7	Un 6	Un 5
Gráfico
Simetría diedral	[8]	[7]	[6]
Un avión de Coxeter	Un 4	Un 3	Un 2
Gráfico
Simetría diedral	[5]	[4]	[3]

El 2-esqueleto del 10-símplex está relacionado topológicamente con el policoron regular abstracto de 11 celdas que tiene los mismos 11 vértices, 55 aristas, pero sólo 1/3 de las caras (55).

• Coxeter, HSM :
  • — (1973). "Tabla I (iii): Politopos regulares, tres politopos regulares en n-dimensiones (n≥5)". Politopos regulares (3.ª ed.). Dover. pp. 296. ISBN 0-486-61480-8.
  • Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Caleidoscopios: escritos selectos de HSM Coxeter. Wiley. ISBN 978-0-471-01003-6.
    • (Artículo 22) — (1940). "Polítopos regulares y semirregulares I". Math. Zeit . 46 : 380–407. doi :10.1007/BF01181449. ISBN 9780471010036.S2CID 186237114  .
    • (Artículo 23) — (1985). "Polítopos regulares y semirregulares II". Math. Zeit . 188 (4): 559–591. doi :10.1007/BF01161657. S2CID  120429557.
    • (Artículo 24) — (1988). "Polítopos regulares y semirregulares III". Math. Zeit . 200 : 3–45. doi :10.1007/BF01161745. S2CID  186237142.
• Conway, John H .; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "26. Hemicubos: 1 _n1 ". Las simetrías de las cosas . pág. 409. ISBN 978-1-56881-220-5.
• Johnson, Norman (1991). Politopos uniformes (manuscrito).
  • Johnson, NW (1966). La teoría de politopos uniformes y panales (PhD). Universidad de Toronto. OCLC  258527038.
• Klitzing, Richard. "Politopos uniformes 10D (polyxenna) x3o3o3o3o3o3o3o3o3o - ux".

• Glosario del hiperespacio, George Olshevsky.
• Politopos de varias dimensiones
• Glosario multidimensional