Lista de politopos regulares
| Polígonos regulares (2D) | |
|---|---|
| Convexo | Estrella |
 {5} |  {5/2} |
| Poliedros regulares (3D) | |
| Convexo | Estrella |
 {5,3} |  {5/2,5} |
| Politopos 4D regulares | |
| Convexo | Estrella |
 {5,3,3} |  {5/2,5,3} |
| Teselaciones regulares en 2D | |
| Euclidiano | Hiperbólico |
 {4,4} |  {5,4} |
| Teselaciones 3D regulares | |
| Euclidiano | Hiperbólico |
 {4,3,4} |  {5,3,4} |
Este artículo enumera los politopos regulares en espacios euclidianos , esféricos e hiperbólicos .
Descripción general
Esta tabla muestra un resumen de los recuentos de politopos regulares por rango.
| Rango | Finito | Euclidiano | Hiperbólico | Abstracto | |||||
|---|---|---|---|---|---|---|---|---|---|
| Compacto | Paracompacto | ||||||||
| Convexo | Estrella | Inclinación [a] [1] | Convexo | Inclinación [a] [1] | Convexo | Estrella | Convexo | ||
| 1 | 1 | ninguno | ninguno | ninguno | ninguno | ninguno | ninguno | ninguno | 1 |
| 2 | ninguno | 1 | ninguno | 1 | ninguno | ninguno | |||
| 3 | 5 | 4 | 9 | 3 | 3 | ||||
| 4 | 6 | 10 | 18 | 1 | 7 | 4 | ninguno | 11 | |
| 5 | 3 | ninguno | 3 | 3 | 15 | 5 | 4 | 2 | |
| 6 | 3 | ninguno | 3 | 1 | 7 | ninguno | ninguno | 5 | |
| 7+ | 3 | ninguno | 3 | 1 | 7 | ninguno | ninguno | ninguno | |
- ^ ab Solo se cuentan los politopos de rango completo. Hay más politopos regulares de cada rango > 1 en dimensiones superiores.
No existen teselaciones de estrellas regulares euclidianas en ningún número de dimensiones.
1-politopos
 | Un diagrama de Coxeter representa los "planos" especulares como nodos y coloca un anillo alrededor de un nodo si un punto no está en el plano. Un dion { }, , es un punto p y su imagen especular, el punto p' , y el segmento de línea entre ellos. , es un punto p y su imagen especular, el punto p' , y el segmento de línea entre ellos. |
Sólo existe un politopo de rango 1 (1-politopo), el segmento de línea cerrado limitado por sus dos puntos finales. Toda realización de este 1-politopo es regular. Tiene el símbolo de Schläfli { }, [2] [3] o un diagrama de Coxeter con un solo nodo en anillo, Norman Johnson lo llama dion [4] y le da el símbolo Schläfli { }.
Norman Johnson lo llama dion [4] y le da el símbolo Schläfli { }.
Aunque es trivial como politopo, aparece como los bordes de polígonos y otros politopos de dimensiones superiores. [5] Se utiliza en la definición de prismas uniformes como el símbolo de Schläfli { }×{p} o el diagrama de Coxeter.



 como un producto cartesiano de un segmento de línea y un polígono regular. [6]
como un producto cartesiano de un segmento de línea y un polígono regular. [6]
2-politopos (polígonos)
Los politopos de rango 2 (2-politopos) se denominan polígonos . Los polígonos regulares son equiláteros y cíclicos . Un polígono regular p -gonal se representa mediante el símbolo de Schläfli {p}.
Muchas fuentes solo consideran polígonos convexos , pero los polígonos estrellados , como el pentagrama , cuando se consideran, también pueden ser regulares. Utilizan los mismos vértices que las formas convexas, pero se conectan en una conectividad alternada que pasa alrededor del círculo más de una vez para completarse.
Convexo
El símbolo de Schläfli {p} representa un p -gono regular .
| Nombre | Triángulo ( 2-símplex ) | Cuadrado ( 2-ortoplex ) ( 2-cubo ) | Pentágono ( politopo de 2 pentagonales ) | Hexágono | Heptágono | Octágono | |
|---|---|---|---|---|---|---|---|
| Colapso | {3} | {4} | {5} | {6} | {7} | {8} | |
| Simetría | D 3 , [3] | D 4 , [4] | D 5 , [5] | D 6 , [6] | D 7 , [7] | D 8 , [8] | |
| Coxeter |    |    |    |    |    |    | |
| Imagen |  |  |  |  |  |  | |
| Nombre | Nonágono (Eneágono) | Decágono | Endecágono | Dodecágono | Tridecágono | Tetradecágono | |
| Colapso | {9} | {10} | {11} | {12} | {13} | {14} | |
| Simetría | D 9 , [9] | D 10 , [10] | D 11 , [11] | D 12 , [12] | D 13 , [13] | D 14 , [14] | |
| Diminuto |    |    |    |    |    |    | |
| Imagen |  |  |  |  |  |  | |
| Nombre | Pentadecágono | Hexadecágono | Heptadecágono | Octadecágono | Eneadecágono | Icoságono | ...p-gon |
| Colapso | {15} | {16} | {17} | {18} | {19} | {20} | { pag } |
| Simetría | D 15 , [15] | D 16 , [16] | D 17 , [17] | D 18 , [18] | D 19 , [19] | D 20 , [20] | D p , [p] |
| Diminuto |    |    |    |    |    |    |    |
| Imagen |  |  |  |  |  |  |  |
Esférico
El dígono regular {2} puede considerarse un polígono regular degenerado . Puede realizarse de forma no degenerada en algunos espacios no euclidianos, como en la superficie de una esfera o un toro . Por ejemplo, el dígono puede realizarse de forma no degenerada como una luna esférica . Un monógono {1} también podría realizarse en la esfera como un único punto con un círculo máximo que lo atraviese. [7] Sin embargo, un monógono no es un politopo abstracto válido porque su única arista incide solo en un vértice en lugar de dos.
| Nombre | Monógono | Digón |
|---|---|---|
| Símbolo de Schläfli | {1} | {2} |
| Simetría | D 1 , [ ] | D 2 , [2] |
| Diagrama de Coxeter |  o o   |    |
| Imagen |  |  |
Estrellas
Existen infinitos politopos regulares en forma de estrella en dos dimensiones, cuyos símbolos de Schläfli consisten en números racionales { n / m } . Se denominan polígonos en forma de estrella y comparten la misma disposición de vértices de los polígonos regulares convexos.
En general, para cualquier número natural n , existen estrellas regulares de n puntas con símbolos de Schläfli { n / m } para todo m tales que m < n /2 (estrictamente hablando { n / m } = { n /( n − m )} ) y m y n son coprimos (por lo tanto, todas las estelaciones de un polígono con un número primo de lados serán estrellas regulares). Los símbolos donde m y n no son coprimos se pueden usar para representar polígonos compuestos.
| Nombre | Pentagrama | Heptagramas | Octagrama | Eneagramas | Decagramo | ... n-gramas | ||
|---|---|---|---|---|---|---|---|---|
| Colapso | {5/2} | {7/2} | {7/3} | {8/3} | {9/2} | {9/4} | {10/3} | { p/q } |
| Simetría | D 5 , [5] | D 7 , [7] | D 8 , [8] | D 9 , [9], | D 10 , [10] | D p , [ p ] | ||
| Coxeter |      |      |      |      |      |      |      |      |
| Imagen |  |  |  |  |  |  |  | |
Pueden existir polígonos estrellados que solo pueden existir como teselas esféricas, de manera similar al monógono y al dígono (por ejemplo: {3/2}, {5/3}, {5/4}, {7/4}, {9/5}), sin embargo, estos no han sido estudiados en detalle.
También existen polígonos estrellados fallidos, como el piangle , que no cubren la superficie de un círculo un número finito de veces. [8]
Polígonos oblicuos
Además de los polígonos regulares planos, existen infinitos polígonos oblicuos regulares . Los polígonos oblicuos se pueden crear mediante la operación de combinación.
La combinación de dos polígonos P y Q , escrita P # Q , se puede construir de la siguiente manera:
- tome el producto cartesiano de sus vértices V P × V Q .
- sumar aristas ( p 0 × q 0 , p 1 × q 1 ) donde ( p 0 , p 1 ) es una arista de P y ( q 0 , q 1 ) es una arista de Q .
- seleccione un componente conectado arbitrario del resultado.
Alternativamente, la mezcla es el polígono ⟨ ρ 0 σ 0 , ρ 1 σ 1 ⟩ donde ρ y σ son los espejos generadores de P y Q colocados en subespacios ortogonales. [9] La operación de mezcla es conmutativa, asociativa e idempotente.
Cada polígono oblicuo regular se puede expresar como la mezcla de un conjunto único [i] de polígonos planos. [9] Si P y Q no comparten factores, entonces Dim( P # Q ) = Dim( P ) + Dim( Q ) .
En 3 espacios
Los polígonos finitos regulares en 3 dimensiones son exactamente las fusiones de los polígonos planos (dimensión 2) con el digón (dimensión 1). Tienen vértices correspondientes a un prisma ( { n / m }#{} donde n es impar) o un antiprisma ( { n / m }#{} donde n es par). Todos los polígonos en el espacio tridimensional tienen un número par de vértices y aristas.
Varios de estos aparecen como polígonos de Petrie de poliedros regulares.
En 4 espacios
Los polígonos finitos regulares en 4 dimensiones son exactamente los polígonos formados como una mezcla de dos polígonos planos distintos. Tienen vértices que se encuentran en un toro de Clifford y están relacionados por un desplazamiento de Clifford . A diferencia de los polígonos tridimensionales, los polígonos oblicuos en rotaciones dobles pueden incluir un número impar de lados.
3-politopos (poliedros)
Los politopos de rango 3 se llaman poliedros :
Un poliedro regular con símbolo de Schläfli { p , q } , diagramas de Coxeter



 , tiene un tipo de cara regular { p } y una figura de vértice regular { q } .
, tiene un tipo de cara regular { p } y una figura de vértice regular { q } .
Una figura de vértice (de un poliedro) es un polígono, que se ve al conectar los vértices que están a una arista de distancia de un vértice dado. Para los poliedros regulares , esta figura de vértice es siempre un polígono regular (y plano).
La existencia de un poliedro regular { p , q } está restringida por una desigualdad, relacionada con el defecto del ángulo de la figura del vértice :
Al enumerar las permutaciones , encontramos cinco formas convexas, cuatro formas de estrella y tres teselas planas, todas con polígonos { p } y { q } limitados a: {3}, {4}, {5}, {5/2} y {6}.
Más allá del espacio euclidiano, hay un conjunto infinito de teselas hiperbólicas regulares.
Convexo
Los cinco poliedros regulares convexos se denominan sólidos platónicos . La cifra de vértices se indica con el recuento de cada vértice. Todos estos poliedros tienen una característica de Euler (χ) de 2.
| Nombre | Pérdida de peso { p , q } | Coxeter     | Imagen (sólida) | Imagen (esfera) | Caras { p } | Bordes | Vértices { q } | Simetría | Dual |
|---|---|---|---|---|---|---|---|---|---|
| Tetraedro ( 3-símplex ) | {3,3} |      |  |  | 4 {3} | 6 | 4 {3} | Td [3,3] (*332 ) | (ser) |
Cubo hexaedro ( 3 cubos ) | {4,3} |      |  |  | 6 {4} | 12 | 8 {3} | Oh [4,3] ( * 432) | Octaedro |
| Octaedro ( 3-ortoplex ) | {3,4} |      |  |  | 8 {3} | 12 | 6 {4} | Oh [4,3] ( * 432) | Cubo |
| Dodecaedro | {5,3} |      |  |  | 12 {5} | 30 | 20 {3} | Yo soy [5,3] (*532) | Icosaedro |
| Icosaedro | {3,5} |      |  |  | 20 {3} | 30 | 12 {5} | Yo soy [5,3] (*532) | Dodecaedro |
Esférico
En geometría esférica existen poliedros esféricos regulares ( teselados de la esfera ) que de otro modo se degenerarían como politopos. Se trata de los hosoedros {2,n} y sus diedros duales {n,2}. Coxeter llama a estos casos teselados "impropios". [10]
A continuación se enumeran los primeros casos (n del 2 al 6).
| Nombre | Colapso {2,p} | Diagrama de Coxeter | Imagen (esfera) | Caras {2} π/p | Bordes | Vértices {p} | Simetría | Dual |
|---|---|---|---|---|---|---|---|---|
| Hosoedro digonal | {2,2} |      | 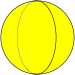 | 2 {2} π/2 | 2 | 2 {2} π/2 | D 2h [2,2] (*222) | Ser |
| Hosoedro trigonal | {2,3} |      |  | 3 {2} π/3 | 3 | 2 {3} | D 3h [2,3] (*322) | Diedro trigonal |
| Hosoedro cuadrado | {2,4} |      | 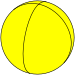 | 4 {2} π/4 | 4 | 2 {4} | D 4h [2,4] (*422) | Diedro cuadrado |
| Hosoedro pentagonal | {2,5} |      |  | 5 {2} π/5 | 5 | 2 {5} | D 5h [2,5] (*522) | Diedro pentagonal |
| Hosoedro hexagonal | {2,6} |      |  | 6 {2} π/6 | 6 | 2 {6} | D 6h [2,6] (*622) | Diedro hexagonal |
| Nombre | Colapso {p,2} | Diagrama de Coxeter | Imagen (esfera) | Caras {p} | Bordes | Vértices {2} | Simetría | Dual |
|---|---|---|---|---|---|---|---|---|
| Diedro digonal | {2,2} |      |  | 2 {2} π/2 | 2 | 2 {2} π/2 | D 2h [2,2] (*222) | Ser |
| Diedro trigonal | {3,2} |      |  | 2 {3} | 3 | 3 {2} π/3 | D 3h [3,2] (*322) | Hosoedro trigonal |
| Diedro cuadrado | {4,2} |      |  | 2 {4} | 4 | 4 {2} π/4 | D 4h [4,2] (*422) | Hosoedro cuadrado |
| Diedro pentagonal | {5,2} |      |  | 2 {5} | 5 | 5 {2} π/5 | D 5h [5,2] (*522) | Hosoedro pentagonal |
| Diedro hexagonal | {6,2} |      |  | 2 {6} | 6 | 6 {2} π/6 | D 6h [6,2] (*622) | Hosoedro hexagonal |
También existen diedros y hosoedros estelares { p / q , 2} y {2, p / q } para cualquier polígono estrellado { p / q } .
Estrellas
Los poliedros estrellados regulares se denominan poliedros de Kepler-Poinsot y son cuatro, basados en las disposiciones de los vértices del dodecaedro {5,3} y el icosaedro {3,5}:
Como teselación esférica , estas formas estelares se superponen a la esfera varias veces, lo que se denomina densidad , siendo 3 o 7 para estas formas. Las imágenes de teselación muestran una única cara de polígono esférico en amarillo.
| Nombre | Imagen (esqueletónica) | Imagen (sólida) | Imagen (esfera) | Diagrama de estelación | Schläfli { p , q } y Coxeter | Caras { p } | Bordes | Vértices { q } verf. | χ | Densidad | Simetría | Dual |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pequeño dodecaedro estrellado |  |  |  |  | {5/2,5}       | 12 {5/2}  | 30 | 12 {5}  | -6 | 3 | Yo soy [5,3] (*532) | Gran dodecaedro |
| Gran dodecaedro |  |  |  |  | {5,5/2}       | 12 {5}  | 30 | 12 {5/2}  | -6 | 3 | Yo soy [5,3] (*532) | Pequeño dodecaedro estrellado |
| Gran dodecaedro estrellado |  |  |  |  | {5/2,3}       | 12 {5/2}  | 30 | 20 {3}  | 2 | 7 | Yo soy [5,3] (*532) | Gran icosaedro |
| Gran icosaedro |  |  |  |  | {3,5/2}       | 20 {3}  | 30 | 12 {5/2}  | 2 | 7 | Yo soy [5,3] (*532) | Gran dodecaedro estrellado |
Hay una cantidad infinita de poliedros estrellados fallidos. También son teselas esféricas con polígonos estrellados en sus símbolos de Schläfli, pero no cubren una esfera un número finito de veces. Algunos ejemplos son {5/2,4}, {5/2,9}, {7/2,3}, {5/2,5/2}, {7/2,7/3}, {4,5/2} y {3,7/3}.
Poliedros oblicuos
![[icono]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | Esta sección necesita ser ampliada . Puedes ayudar agregándole algo. ( Enero de 2024 ) |
Los poliedros oblicuos regulares son generalizaciones del conjunto de poliedros regulares que incluyen la posibilidad de figuras de vértices no planas .
Para los poliedros oblicuos de cuatro dimensiones, Coxeter propuso un símbolo de Schläfli modificado {l,m|n} para estas figuras, donde {l,m} implica la figura del vértice , m l-gonos alrededor de un vértice y n agujeros en el gonal. Sus figuras de vértice son polígonos oblicuos que zigzaguean entre dos planos.
Los poliedros oblicuos regulares, representados por {l,m|n}, siguen esta ecuación:
Cuatro de ellos pueden verse en 4 dimensiones como un subconjunto de caras de cuatro 4-politopos regulares , que comparten la misma disposición de vértices y disposición de aristas :
 |  |  |  |
| {4, 6 | 3} | {6, 4 | 3} | {4, 8 | 3} | {8, 4 | 3} |
|---|
4-politopos
Los 4-politopos regulares con símbolo Schläfli tienen celdas de tipo , caras de tipo , figuras de arista y figuras de vértice .
- Una figura de vértice (de un 4-politopo) es un poliedro, visto por la disposición de los vértices vecinos alrededor de un vértice dado. Para los 4-politopos regulares, esta figura de vértice es un poliedro regular.
- Una figura de arista es un polígono, que se ve por la disposición de las caras alrededor de una arista. Para los 4-politopos regulares, esta figura de arista siempre será un polígono regular.
La existencia de un 4-politopo regular está limitada por la existencia de los poliedros regulares . Un nombre sugerido para los 4-politopos es "policoronte". [11]
Cada uno existirá en un espacio dependiente de esta expresión:
- : Panal hiperesférico de 3 espacios o 4 politopos
- : Panal euclidiano de 3 espacios
- : Panal hiperbólico de 3 espacios
Estas restricciones permiten 21 formas: 6 son convexas, 10 son no convexas, una es un panal euclidiano de 3 espacios y 4 son panales hiperbólicos.
La característica de Euler para 4-politopos convexos es cero:
Convexo
En la siguiente tabla se muestran los 6 4-politopos regulares convexos. Todos estos 4-politopos tienen una característica de Euler (χ) de 0.
| Nombre | Deslizadores {p,q,r} | Coxeter       | Células {p,q} | Caras {p} | Bordes {r} | Vértices {q,r} | Doble {r,q,p} |
|---|---|---|---|---|---|---|---|
| 5 celdas ( 4-símplex ) | {3,3,3} |        | 5 {3,3} | 10 {3} | 10 {3} | 5 {3,3} | (ser) |
| 8 celdas ( 4 cubos ) (Tesseract) | {4,3,3} |        | 8 {4,3} | 24 {4} | 32 {3} | 16 {3,3} | 16 celdas |
| 16 células ( 4-ortoplex ) | {3,3,4} |        | 16 {3,3} | 32 {3} | 24 {4} | 8 {3,4} | Teseracto |
| 24 celdas | {3,4,3} |        | 24 {3,4} | 96 {3} | 96 {3} | 24 {4,3} | (ser) |
| 120 celdas | {5,3,3} |        | 120 {5,3} | 720 {5} | 1200 {3} | 600 {3,3} | 600 celdas |
| 600 celdas | {3,3,5} |        | 600 {3,3} | 1200 {3} | 720 {5} | 120 {3,5} | 120 celdas |
| 5 celdas | 8 celdas | 16 celdas | 24 celdas | 120 celdas | 600 celdas |
|---|---|---|---|---|---|
| {3,3,3} | {4,3,3} | {3,3,4} | {3,4,3} | {5,3,3} | {3,3,5} |
| Proyecciones ortográficas sesgadas de estructuras alámbricas ( polígonos de Petrie ) | |||||
 |  |  |  |  |  |
| Proyecciones ortográficas sólidas | |||||
 envoltura tetraédrica ( centrada en la célula/vértice) |  envoltura cúbica (centrada en la celda) |  envoltura cúbica (centrada en la celda) |  envoltura cuboctaédrica (centrada en la célula) |  envoltura de triacontaedro rómbico truncado (centrado en la célula) |  Envolvente icosidodecaédrica de Pentakis (centrada en el vértice) |
| Diagramas de Schlegel en alambre ( proyección en perspectiva ) | |||||
 (centrado en la célula) |  (centrado en la célula) |  (centrado en la célula) |  (centrado en la célula) |  (centrado en la célula) |  (centrado en el vértice) |
| Proyecciones estereográficas de estructura alámbrica ( hipersféricas ) | |||||
 |  |  |  |  |  |
Esférico
Los di-4-topos y hoso-4-topos existen como teselaciones regulares de la 3-esfera .
Los di-4-topos regulares (2 facetas) incluyen: {3,3,2}, {3,4,2}, {4,3,2}, {5,3,2}, {3,5,2}, {p,2,2}, y sus duales hoso-4-topos (2 vértices): {2,3,3}, {2,4,3}, {2,3,4}, {2,3,5}, {2,5,3}, {2,2, p }. Los 4-politopos de la forma {2, p ,2} son los mismos que {2,2, p }. También existen los casos { p ,2, q } que tienen celdas diedras y figuras de vértice hosoédricas.
| Deslizamiento {2, p , q } | Coxeter       | Células {2, p } π/ q | Caras {2} π/ p ,π/ q | Bordes | Vértices | Figura de vértice { p , q } | Simetría | Dual |
|---|---|---|---|---|---|---|---|---|
| {2,3,3} |        | 4 {2,3} π/3  | 6 {2} π/3,π/3 | 4 | 2 | {3,3} | [2,3,3] | {3,3,2} |
| {2,4,3} |        | 6 {2,4} π/3  | 12 {2} π/4,π/3 | 8 | 2 | {4,3} | [2,4,3] | {3,4,2} |
| {2,3,4} |        | 8 {2,3} π/4  | 12 {2} π/3,π/4 | 6 | 2 | {3,4} | [2,4,3] | {4,3,2} |
| {2,5,3} |        | 12 {2,5} π/3  | 30 {2} π/5,π/3 | 20 | 2 | {5,3} | [2,5,3] | {3,5,2} |
| {2,3,5} |        | 20 {2,3} π/5  | 30 {2} π/3,π/5 | 12 | 2 | {3,5} | [2,5,3] | {5,3,2} |
Estrellas
Hay diez politopos de estrella regulares , que se denominan politopos de Schläfli–Hess . Sus vértices se basan en los politopos convexos de 120 celdas {5,3,3} y 600 celdas {3,3,5} .
Ludwig Schläfli encontró cuatro de ellos y se saltó los últimos seis porque no permitiría formas que no cumplieran la característica de Euler en celdas o figuras de vértices (para toros de agujero cero: F+V−E=2). Edmund Hess (1843-1903) completó la lista completa de diez en su libro alemán Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder (1883)[1].
Hay 4 disposiciones de aristas únicas y 7 disposiciones de caras únicas de estos 10 4-politopos de estrella regulares, que se muestran como proyecciones ortogonales :
| Nombre | Estructura alámbrica | Sólido | Pérdida de peso {p, q, r} Coxeter | Células {p, q} | Caras {p} | Bordes {r} | Vértices {q, r} | Densidad | χ | Grupo de simetría | Dual {r, q, p} |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Icosaédrica de 120 celdas (facetada de 600 celdas) |  |  | {3,5,5/2}         | 120 {3,5}  | 1200 {3}  | 720 {5/2}  | 120 {5,5/2}  | 4 | 480 | H4 [5,3,3 ] | Pequeña estrella de 120 celdas |
| Pequeña estrella de 120 celdas |  |  | {5/2,5,3}         | 120 {5/2,5}  | 720 {5/2}  | 1200 {3}  | 120 {5,3}  | 4 | −480 | H4 [5,3,3 ] | Icosaédrica de 120 celdas |
| Gran 120 celdas |  |  | {5,5/2,5}         | 120 {5,5/2}  | 720 {5}  | 720 {5}  | 120 {5/2,5}  | 6 | 0 | H4 [5,3,3 ] | Auto-dual |
| Gran 120 celdas |  |  | {5,3,5/2}         | 120 {5,3}  | 720 {5}  | 720 {5/2}  | 120 {3,5/2}  | 20 | 0 | H4 [5,3,3 ] | Gran estrella de 120 celdas |
| Gran estrella de 120 celdas |  |  | {5/2,3,5}         | 120 {5/2,3}  | 720 {5/2}  | 720 {5}  | 120 {3,5}  | 20 | 0 | H4 [5,3,3 ] | Gran 120 celdas |
| Gran estrella de 120 celdas |  |  | {5/2,5,5/2}           | 120 {5/2,5}  | 720 {5/2}  | 720 {5/2}  | 120 {5,5/2}  | 66 | 0 | H4 [5,3,3 ] | Auto-dual |
| Gran gran 120 celdas |  |  | {5,5/2,3}         | 120 {5,5/2}  | 720 {5}  | 1200 {3}  | 120 {5/2,3}  | 76 | −480 | H4 [5,3,3 ] | Gran icosaédrico de 120 celdas |
| Gran icosaédrico de 120 celdas (gran facetado de 600 celdas) |  |  | {3,5/2,5}         | 120 {3,5/2}  | 1200 {3}  | 720 {5}  | 120 {5/2,5}  | 76 | 480 | H4 [5,3,3 ] | Gran gran 120 celdas |
| Gran 600 celdas |  |  | {3,3,5/2}         | 600 {3,3}  | 1200 {3}  | 720 {5/2}  | 120 {3,5/2}  | 191 | 0 | H4 [5,3,3 ] | Gran gran estrella de 120 celdas |
| Gran gran estrella de 120 celdas |  |  | {5/2,3,3}         | 120 {5/2,3}  | 720 {5/2}  | 1200 {3}  | 600 {3,3}  | 191 | 0 | H4 [5,3,3 ] | Gran 600 celdas |
Existen 4 posibles permutaciones fallidas de 4 politopos de estrellas regulares: {3,5/2,3}, {4,3,5/2}, {5/2,3,4}, {5/2,3,5/2}. Sus celdas y figuras de vértices existen, pero no cubren una hiperesfera con un número finito de repeticiones.
4-politopos sesgados
![[icono]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | Esta sección necesita ser ampliada . Puedes ayudar agregándole algo. ( Enero de 2024 ) |
Además de los 16 4-politopos planares anteriores, hay 18 politopos oblicuos finitos. [12] Uno de ellos se obtiene como el Petrial del teseracto, y los otros 17 se pueden formar aplicando la operación kappa a los politopos planares y al Petrial del teseracto.
Rangos 5 y superiores
A los 5 politopos se les puede dar el símbolo donde es el tipo de 4 caras, es el tipo de celda, es el tipo de cara y es la figura de la cara, es la figura del borde y es la figura del vértice.
- Una figura de vértice (de un 5-politopo) es un 4-politopo, visto por la disposición de los vértices vecinos a cada vértice.
- Una figura de arista (de un 5-politopo) es un poliedro, visto por la disposición de las caras alrededor de cada arista.
- Una figura facial (de un politopo 5) es un polígono, visto por la disposición de las celdas alrededor de cada cara.
Un 5-politopo regular existe solo si y son 4-politopos regulares.
El espacio en el que encaja se basa en la expresión:
- :Teselación esférica de 4 espacios o politopo de 5 espacios
- :Teselación euclidiana de 4 espacios
- : teselación hiperbólica de 4 espacios
La enumeración de estas restricciones produce 3 politopos convexos, ningún politopo estrella, 3 teselaciones de 4-espacios euclidianos y 5 teselaciones de 4-espacios hiperbólicos paracompactos. Los únicos politopos regulares no convexos para los rangos 5 y superiores son los sesgados.
Convexo
En dimensiones 5 y superiores, solo hay tres tipos de politopos regulares convexos. [13]
| Nombre | Símbolo de Schläfli {p 1 ,...,p n −1 } | Coxeter | k -caras | Tipo de faceta | Figura de vértice | Dual |
|---|---|---|---|---|---|---|
| n -símplex | {3 n −1 } |     ... ...    | {3 n −2 } | {3 n −2 } | Auto-dual | |
| n -cubo | {4,3 n −2 } |     ... ...    | {4,3 n −3 } | {3 n −2 } | n -ortoplex | |
| n -ortoplex | {3 n −2 ,4} |     ... ...    | {3 n −2 } | {3 n −3 ,4} | n -cubo |
También hay casos impropios en los que algunos números en el símbolo de Schläfli son 2. Por ejemplo, {p,q,r,...2} es un politopo esférico regular impropio siempre que {p,q,r...} sea un politopo esférico regular, y {2,...p,q,r} es un politopo esférico regular impropio siempre que {...p,q,r} sea un politopo esférico regular. Dichos politopos también pueden usarse como facetas, dando lugar a formas como {p,q,...2...y,z}.
5 dimensiones
| Nombre | Símbolo de Schläfli {p,q,r,s} Coxeter | Facetas {p,q,r} | Células {p,q} | Caras {p} | Bordes | Vértices | Figura de la cara {s} | Figura de borde {r,s} | Figura de vértice {q,r,s} |
|---|---|---|---|---|---|---|---|---|---|
| 5-símplex | {3,3,3,3}         | 6 {3,3,3} | 15 {3,3} | 20 {3} | 15 | 6 | {3} | {3,3} | {3,3,3} |
| 5 cubos | {4,3,3,3}         | 10 {4,3,3} | 40 {4,3} | 80 {4} | 80 | 32 | {3} | {3,3} | {3,3,3} |
| 5-ortoplex | {3,3,3,4}         | 32 {3,3,3} | 80 {3,3} | 80 {3} | 40 | 10 | {4} | {3,4} | {3,3,4} |
 5-símplex |  5 cubos |  5-ortoplex |
6 dimensiones
| Nombre | Colapso | Vértices | Bordes | Caras | Células | 4 caras | 5 caras | χ |
|---|---|---|---|---|---|---|---|---|
| 6-símplex | {3,3,3,3,3} | 7 | 21 | 35 | 35 | 21 | 7 | 0 |
| 6 cubos | {4,3,3,3,3} | 64 | 192 | 240 | 160 | 60 | 12 | 0 |
| 6-ortoplex | {3,3,3,3,4} | 12 | 60 | 160 | 240 | 192 | 64 | 0 |
 6-símplex |  6 cubos |  6-ortoplex |
7 dimensiones
| Nombre | Colapso | Vértices | Bordes | Caras | Células | 4 caras | 5 caras | 6 caras | χ |
|---|---|---|---|---|---|---|---|---|---|
| 7-símplex | {3,3,3,3,3,3} | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 2 |
| 7 cubos | {4,3,3,3,3,3} | 128 | 448 | 672 | 560 | 280 | 84 | 14 | 2 |
| 7-ortoplex | {3,3,3,3,3,4} | 14 | 84 | 280 | 560 | 672 | 448 | 128 | 2 |
 7-símplex |  7 cubos |  7-ortoplex |
8 dimensiones
| Nombre | Colapso | Vértices | Bordes | Caras | Células | 4 caras | 5 caras | 6 caras | 7 caras | χ |
|---|---|---|---|---|---|---|---|---|---|---|
| 8-símplex | {3,3,3,3,3,3,3} | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 0 |
| 8 cubos | {4,3,3,3,3,3,3} | 256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 0 |
| 8-ortoplex | {3,3,3,3,3,3,4} | 16 | 112 | 448 | 1120 | 1792 | 1792 | 1024 | 256 | 0 |
 8-símplex |  8 cubos |  8-ortoplex |
9 dimensiones
| Nombre | Colapso | Vértices | Bordes | Caras | Células | 4 caras | 5 caras | 6 caras | 7 caras | 8 caras | χ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 9-símplex | {3 8 } | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 2 |
| 9 cubos | {4,3 7 } | 512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 | 2 |
| 9-ortoplex | {3 7 ,4} | 18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 | 2 |
 9-símplex |  9 cubos |  9-ortoplex |
10 dimensiones
| Nombre | Colapso | Vértices | Bordes | Caras | Células | 4 caras | 5 caras | 6 caras | 7 caras | 8 caras | 9 caras | χ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10-símplex | {3 9 } | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 0 |
| 10 cubos | {4,3 8 } | 1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 | 0 |
| 10-ortoplex | {3 8 ,4} | 20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | 0 |
 10-símplex |  10 cubos |  10-ortoplex |
Politopos estelares
No hay politopos estelares regulares de rango 5 o superior, con la excepción de politopos degenerados creados por el producto estelar de politopos estelares de rango inferior, por ejemplo, hosótopos y dítopos.
Politopos proyectivos regulares
Existe un politopo proyectivo regular ( n +1) cuando una teselación n -esférica regular original, {p,q,...}, es simétrica centralmente . Un politopo de este tipo se denomina hemi-{p,q,...} y contiene la mitad de elementos. Coxeter da un símbolo {p,q,...}/2, mientras que McMullen escribe {p,q,...} h/2 con h como el número de Coxeter . [14]
Los polígonos regulares de lados pares tienen polígonos proyectivos de hemi- 2n -ágonos, {2p}/2.
Hay 4 poliedros proyectivos regulares relacionados con 4 de los 5 sólidos platónicos .
El hemicubo y el hemioctaedro se generalizan como hemi- n -cubos y hemi -n - ortoplexos a cualquier rango.
Poliedros proyectivos regulares
| Nombre | Coxeter McMullen | Imagen | Caras | Bordes | Vértices | χ | gráfico de esqueleto |
|---|---|---|---|---|---|---|---|
| Hemicubo | {4,3}/2 {4,3} 3 |  | 3 | 6 | 4 | 1 | K 4 |
| Hemioctaedro | {3,4}/2 {3,4} 3 |  | 4 | 6 | 3 | 1 | K 3 de doble filo |
| Hemidodecaedro | {5,3}/2 {5,3} 5 |  | 6 | 15 | 10 | 1 | G(5,2) |
| Hemiicosaedro | {3,5}/2 {3,5} 5 |  | 10 | 15 | 6 | 1 | K 6 |
4-politopos proyectivos regulares
5 de los 6 politopos cuadripolares convexos regulares son politopos cuadripolares proyectivos generadores simétricos centralmente. Los 3 casos especiales son hemi-24-celdas, hemi-600-celdas y hemi-120-celdas.
| Nombre | Símbolo de Coxeter | Símbolo de McMullen | Células | Caras | Bordes | Vértices | χ | Gráfico de esqueleto |
|---|---|---|---|---|---|---|---|---|
| Hemiteseracto | {4,3,3}/2 | {4,3,3} 4 | 4 | 12 | 16 | 8 | 0 | K 4,4 |
| Hemi- 16 células | {3,3,4}/2 | {3,3,4} 4 | 8 | 16 | 12 | 4 | 0 | K 4 de doble filo |
| Hemi- 24 células | {3,4,3}/2 | {3,4,3} 6 | 12 | 48 | 48 | 12 | 0 | |
| Hemi- 120 células | {5,3,3}/2 | {5,3,3} 15 | 60 | 360 | 600 | 300 | 0 | |
| Hemi- 600 celdas | {3,3,5}/2 | {3,3,5} 15 | 300 | 600 | 360 | 60 | 0 |
5-politopos proyectivos regulares
Solo 2 de los 3 politopos esféricos regulares son simétricos centralmente para los rangos 5 o superiores. Los politopos proyectivos regulares correspondientes son las versiones hemi del hipercubo y el ortoplex regulares. Se presentan en una tabla a continuación para el rango 5, por ejemplo:
| Nombre | Colapso | 4 caras | Células | Caras | Bordes | Vértices | χ | Gráfico de esqueleto |
|---|---|---|---|---|---|---|---|---|
| hemi- penteracto | {4,3,3,3}/2 | 5 | 20 | 40 | 40 | 16 | 1 | Esqueleto de teseracto + 8 diagonales centrales |
| hemi- pentacross | {3,3,3,4}/2 | 16 | 40 | 40 | 20 | 5 | 1 | K 5 de doble filo |
Apeirotopos
Un apeirótopo o politopo infinito es un politopo que tiene infinitas facetas . Un n -apeirotopo es un n -politopo infinito: un 2-apeirotopo o apeirógono es un polígono infinito, un 3-apeirotopo o apeiroedro es un poliedro infinito, etc.
Hay dos clases geométricas principales de apeirótopos: [15]
- Panales regulares de n dimensiones, que llenan completamente un espacio n -dimensional.
- Apeirotopos regulares oblicuos , que comprenden una variedad n -dimensional en un espacio superior.
2-apeirotopos (apeirogones)
El apeirógono recto es una teselación regular de la línea, que la subdivide en infinitos segmentos iguales. Tiene infinitos vértices y aristas. Su símbolo de Schläfli es {∞} y el diagrama de Coxeter

 .
.
Existe como límite del p -gono cuando p tiende a infinito, de la siguiente manera:
| Nombre | Monógono | Digón | Triángulo | Cuadrado | Pentágono | Hexágono | Heptágono | p-gon | Apeirogon |
|---|---|---|---|---|---|---|---|---|---|
| Colapso | {1} | {2} | {3} | {4} | {5} | {6} | {7} | { pag } | {∞} |
| Simetría | D 1 , [ ] | D 2 , [2] | D 3 , [3] | D 4 , [4] | D 5 , [5] | D 6 , [6] | D 7 , [7] | [pag] | |
| Coxeter |  o o   |    |    |    |    |    |    |    |    |
| Imagen |  |  |  |  |  |  |  |  |
Los apeirógonos en el plano hiperbólico , más notablemente el apeirógono regular , {∞}, pueden tener una curvatura al igual que los polígonos finitos del plano euclidiano, con los vértices circunscritos por horociclos o hiperciclos en lugar de círculos .
Los apeirógonos regulares que están escalados para converger en el infinito tienen el símbolo {∞} y existen en horociclos, mientras que, de manera más general, pueden existir en hiperciclos.
| {∞} | {πi/λ} |
|---|---|
 Apeirogon en horociclo |  Apeirogon sobre el hiperciclo |
Arriba hay dos apeirógonos hiperbólicos regulares en el modelo de disco de Poincaré , el de la derecha muestra líneas de reflexión perpendiculares de dominios fundamentales divergentes , separadas por una longitud λ.
Apeirogones oblicuos
Un apeirógono oblicuo en dos dimensiones forma una línea en zigzag en el plano. Si el zigzag es parejo y simétrico, entonces el apeirógono es regular.
Los apeirógonos oblicuo se pueden construir en cualquier número de dimensiones. En tres dimensiones, un apeirógono oblicuo regular traza una espiral helicoidal y puede ser levógiro o dextrógiro.
| 2 dimensiones | 3 dimensiones |
|---|---|
 Apeirogon en zigzag |  Apeirogon de hélice |
3-apeirotopos (apeiroedros)
Teselación euclidiana
Hay tres teselaciones regulares del plano.
| Nombre | Azulejos cuadrados (cuadrícula) | Teselación triangular (deltille) | Azulejos hexagonales (hextille) |
|---|---|---|---|
| Simetría | p4m, [4,4], (*442) | p6m, [6,3], (*632) | |
| Colapso {p,q} | {4,4} | {3,6} | {6,3} |
| Diagrama de Coxeter |      |      |      |
| Imagen |  |  |  |
Hay dos teselaciones regulares impropias: {∞,2}, un diedro apeirogonal , formado por dos apeirógonos , cada uno de los cuales llena la mitad del plano; y, en segundo lugar, su dual, {2,∞}, un hosoedro apeirogonal , visto como un conjunto infinito de líneas paralelas.
 {∞,2} ,      |  {2,∞} ,      |
Teselación de estrellas euclidianas
No existen teselas planas regulares de polígonos estrellados . Hay muchas enumeraciones que caben en el plano (1/ p + 1/ q = 1/2), como {8/3,8}, {10/3,5}, {5/2,10}, {12/5,12}, etc., pero ninguna se repite periódicamente.
Teselación hiperbólica
Las teselaciones del 2-espacio hiperbólico son teselas hiperbólicas . Hay infinitas teselas regulares en H 2 . Como se indicó anteriormente, cada par de números enteros positivos { p , q } tal que 1/ p + 1/ q < 1/2 da una tesela hiperbólica. De hecho, para el triángulo de Schwarz general ( p , q , r ) lo mismo es válido para 1/ p + 1/ q + 1/ r < 1.
Hay varias formas diferentes de representar el plano hiperbólico, incluido el modelo de disco de Poincaré , que convierte el plano en un círculo, como se muestra a continuación. Debe tenerse en cuenta que todas las caras de los polígonos en los mosaicos que se muestran a continuación tienen el mismo tamaño y solo parecen hacerse más pequeñas cerca de los bordes debido a la proyección aplicada, de forma muy similar al efecto de la lente ojo de pez de una cámara .
Hay infinitos 3-apeirotopos (apeiroedros) planos regulares como teselaciones regulares del plano hiperbólico, de la forma {p,q}, con p+q<pq/2.
- {3,7}, {3,8}, {3,9} ... {3,∞}
- {4,5}, {4,6}, {4,7} ... {4,∞}
- {5,4}, {5,5}, {5,6} ... {5,∞}
- {6,4}, {6,5}, {6,6} ... {6,∞}
- {7,3}, {7,4}, {7,5} ... {7,∞}
- {8,3}, {8,4}, {8,5} ... {8,∞}
- {9,3}, {9,4}, {9,5} ... {9,∞}
- ...
- {∞,3}, {∞,4}, {∞,5} ... {∞,∞}
Una muestra:
| Tabla de mosaico hiperbólico regular | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Teselaciones esféricas (impropias / platónicas) / euclidianas /hiperbólicas (disco de Poincaré: compactas / paracompactas / no compactas ) con su símbolo de Schläfli | |||||||||||
| p \ q | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... | ∞ | ... | iπ/λ |
| 2 |  {2 , 2}      |  {2,3}      |  {2,4}      |  {2,5}      |  {2,6}      |  {2,7}      |  {2,8}      |  {2,∞}      |  {2,iπ/λ}      | ||
| 3 |  {3,2}      |  ( tetraedro ) {3,3}      |  ( octaedro ) {3,4}      |  ( icosaedro ) {3,5}      |  ( deltille ) {3,6}      |  {3,7}      |  {3,8}      |  {3,∞}      |  {3,iπ/λ}      | ||
| 4 |  {4,2}      |  ( cubo ) {4,3}      |  ( cuadrilla ) {4,4}      |  {4,5}      |  {4,6}      |  {4,7}      |  {4,8}      |  {4,∞}      |  {4,iπ/λ}      | ||
| 5 |  {5,2}      |  ( dodecaedro ) {5,3}      |  {5,4}      |  {5,5}      |  {5,6}      |  {5,7}      |  {5,8}      |  {5,∞}      |  {5,iπ/λ}      | ||
| 6 |  {6,2}      |  ( hexágono ) {6,3}      |  {6,4}      |  {6,5}      |  {6,6}      |  {6,7}      |  {6,8}      |  {6,∞}      |  {6,iπ/λ}      | ||
| 7 | {7,2}     |  {7,3}      |  {7,4}      |  {7,5}      |  {7,6}      |  {7,7}      |  {7,8}      |  {7,∞}      | {7,iπ/λ}     | ||
| 8 | {8,2}     |  {8,3}      |  {8,4}      |  {8,5}      |  {8,6}      |  {8,7}      |  {8,8}      |  {8,∞}      | {8,iπ/λ}     | ||
| ... | |||||||||||
| ∞ |  {∞,2}      |  {∞,3}      |  {∞,4}      |  {∞,5}      |  {∞,6}      |  {∞,7}      |  {∞,8}      |  {∞,∞}      |  {∞,iπ/λ}      | ||
| ... | |||||||||||
| iπ/λ |  {iπ/λ,2}      |  {iπ/λ,3}      |  {iπ/λ,4}      |  {iπ/λ,5}      |  {iπ/λ,6}      | {iπ/λ,7}     | {iπ/λ,8}     |  {iπ/λ,∞}      |  {iπ/λ, iπ/λ} | ||
Los mosaicos {p, ∞} tienen vértices ideales , en el borde del modelo del disco de Poincaré. Sus duales {∞, p} tienen caras apeirogonales ideales , lo que significa que están inscritos en horociclos . Se podría ir más allá (como se hace en la tabla anterior) y encontrar mosaicos con vértices ultra-ideales, fuera del disco de Poincaré, que sean duales a mosaicos inscritos en hiperciclos ; en lo que se simboliza {p, iπ/λ} arriba, infinitas teselas todavía encajan alrededor de cada vértice ultra-ideal. [16] (Las líneas paralelas en el espacio hiperbólico extendido se encuentran en un punto ideal; las líneas ultraparalelas se encuentran en un punto ultra-ideal.) [17]
Teselación estelar hiperbólica
Hay 2 formas infinitas de teselaciones hiperbólicas cuyas caras o figuras de vértice son polígonos estrellados: { m /2, m } y sus duales { m , m /2} con m = 7, 9, 11, .... [18] Las teselaciones { m /2, m } son estelaciones de las teselaciones { m , 3} mientras que las teselaciones duales { m , m /2} son facetas de las teselaciones {3, m } y agrandamientos [ii] de las teselaciones { m , 3}.
Los patrones { m /2, m } y { m , m /2} continúan para m < 7 impar como poliedros : cuando m = 5, obtenemos el pequeño dodecaedro estrellado y el gran dodecaedro , [18] y cuando m = 3, el caso degenera a un tetraedro . Los otros dos poliedros de Kepler-Poinsot (el gran dodecaedro estrellado y el gran icosaedro ) no tienen análogos de teselaciones hiperbólicas regulares. Si m es par, dependiendo de cómo elijamos definir { m /2}, podemos obtener cubiertas dobles degeneradas de otras teselaciones o teselaciones compuestas .
| Nombre | Colapso | Diagrama de Coxeter | Imagen | Tipo de rostro {p} | Figura de vértice {q} | Densidad | Simetría | Dual |
|---|---|---|---|---|---|---|---|---|
| Orden-7 mosaico heptagramático | {7/2,7} |        |  | {7/2} | {7} | 3 | *732 [7,3] | Teselación heptagonal según orden heptagramático |
| Teselación heptagonal según orden heptagramático | {7,7/2} |        |  | {7} | {7/2} | 3 | *732 [7,3] | Orden-7 mosaico heptagramático |
| Orden 9: mosaico eneagramático | {9/2,9} |        |  | {9/2} | {9} | 3 | *932 [9,3] | Teselación eneagonal según orden eneagramático |
| Teselación eneagonal según orden eneagramático | {9,9/2} |        |  | {9} | {9/2} | 3 | *932 [9,3] | Orden 9: mosaico eneagramático |
| Teselación endecagramática de orden 11 | {11/2,11} |        |  | {11/2} | {11} | 3 | *11.3.2 [11,3] | Teselación endecagonal de orden hendecagramático |
| Teselación endecagonal de orden hendecagramático | {11,11/2} |        |  | {11} | {11/2} | 3 | *11.3.2 [11,3] | Teselación endecagramática de orden 11 |
| Orden- p p - teselación gramatical | { p /2, p } |        | { pág . 2 } | { pag } | 3 | * pág. 32 [pág. 3] | orden p -grammico teselado p -gonal | |
| orden p -grammico teselado p -gonal | { p , p /2} |        | { pag } | { pág . 2 } | 3 | * pág. 32 [pág. 3] | Orden- p p - teselación gramatical |
Apeiroedros oblicuos en el espacio tridimensional euclidiano
![[icono]](http://upload.wikimedia.org/wikipedia/commons/thumb/1/1c/Wiki_letter_w_cropped.svg/20px-Wiki_letter_w_cropped.svg.png) | Esta sección necesita ser ampliada . Puedes ayudar agregándole algo. ( Enero de 2024 ) |
Hay tres apeiroedros oblicuos regulares en el espacio tridimensional euclidiano, con caras planas. [19] [20] [21] Comparten la misma disposición de vértices y disposición de aristas de tres panales convexos uniformes .
- 6 cuadrados alrededor de cada vértice: {4,6|4}
- 4 hexágonos alrededor de cada vértice: {6,4|4}
- 6 hexágonos alrededor de cada vértice: {6,6|3}

| Poliedros oblicuos regulares con caras planas | ||
|---|---|---|
 {4,6|4} |  {6,4|4} |  {6,6|3} |
Teniendo en cuenta las caras oblicuas, hay 24 apeiroedros regulares en el espacio tridimensional euclidiano. [23] Estos incluyen 12 apeiroedros creados por mezclas con los apeiroedros euclidianos y 12 apeiroedros puros, incluidos los 3 anteriores, que no se pueden expresar como una mezcla no trivial.
Estos apeiroedros puros son:
- {4,6|4} , el mucubo
- {∞,6} 4,4 , el Petrial del mucubo
- {6,6|3} , el mutetraedro
- {∞,6} 6,3 , el petrial del mutetraedro
- {6,4|4} , el muoctaedro
- {∞,4} 6,4 , el Petrial del muoctaedro
- {6,6} 4 , la reducción a la mitad del mucubo
- {4,6} 6 , el Petrial de {6,6} 4
- {∞,4} ·,*3 , la inclinación del muoctaedro
- {6,4} 6 , el Petrial de {∞,4} ·,*3
- {∞,3} ( a )
- {∞,3} ( b )
Apeiroedros oblicuos en el espacio tridimensional hiperbólico
Hay 31 apeiroedros oblicuos regulares con caras convexas en el espacio tridimensional hiperbólico con simetría compacta o paracompacta: [24]
- 14 son compactos: {8,10|3}, {10,8|3}, {10,4|3}, {4,10|3}, {6,4|5}, {4,6|5}, {10,6|3}, {6,10|3}, {8,8|3}, {6,6|4}, {10,10|3},{6,6|5}, {8,6|3} y {6,8|3}.
- 17 son paracompactos: {12,10|3}, {10,12|3}, {12,4|3}, {4,12|3}, {6,4|6}, {4,6|6}, {8,4|4}, {4,8|4}, {12,6|3}, {6,12|3}, {12,12|3}, {6,6|6}, {8,6|4}, {6,8|4}, {12,8|3}, {8,12|3} y {8,8|4}.
4-apeirotopos
Teselaciones del espacio tridimensional euclidiano

Sólo existe una teselación regular no degenerada de 3-espacios ( panales ), {4, 3, 4}: [25]
| Nombre | Deslizadores {p,q,r} | Coxeter       | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de borde {r} | Figura de vértice {q,r} | χ | Dual |
|---|---|---|---|---|---|---|---|---|
| Panal cúbico | {4,3,4} |        | {4,3} | {4} | {4} | {3,4} | 0 | Auto-dual |
Teselaciones impropias del espacio tridimensional euclidiano

Hay seis teselaciones regulares impropias, pares basados en los tres mosaicos euclidianos regulares. Sus celdas y figuras de vértice son todos hosoedros regulares {2,n}, diedros {n,2} y mosaicos euclidianos. Estos mosaicos regulares impropias están relacionados constructivamente con panales prismáticos uniformes mediante operaciones de truncamiento. Son análogos de dimensiones superiores del mosaico apeirogonal de orden 2 y del hosoedro apeirogonal .
| Deslizadores {p,q,r} | Diagrama de Coxeter | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de borde {r} | Figura de vértice {q,r} |
|---|---|---|---|---|---|
| {2,4,4} |        | {2,4} | {2} | {4} | {4,4} |
| {2,3,6} |        | {2,3} | {2} | {6} | {3,6} |
| {2,6,3} |        | {2,6} | {2} | {3} | {6,3} |
| {4,4,2} |        | {4,4} | {4} | {2} | {4,2} |
| {3,6,2} |        | {3,6} | {3} | {2} | {6,2} |
| {6,3,2} |        | {6,3} | {6} | {2} | {3,2} |
Teselaciones del espacio tridimensional hiperbólico
Hay 15 panales planos regulares de 3-espacios hiperbólicos:
- 4 son compactos: {3,5,3}, {4,3,5}, {5,3,4} y {5,3,5}
- mientras que 11 son paracompactos: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} y {6,3,6}.
| ||||
|
Las teselaciones del espacio hiperbólico 3 pueden denominarse panales hiperbólicos . Hay 15 panales hiperbólicos en H 3 , 4 compactos y 11 paracompactos.
| Nombre | Símbolo de Schläfli {p,q,r} | Coxeter       | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de borde {r} | Figura de vértice {q,r} | χ | Dual |
|---|---|---|---|---|---|---|---|---|
| Panal icosaédrico | {3,5,3} |        | {3,5} | {3} | {3} | {5,3} | 0 | Auto-dual |
| Orden-5 panal cúbico | {4,3,5} |        | {4,3} | {4} | {5} | {3,5} | 0 | {5,3,4} |
| Panal dodecaédrico de orden 4 | {5,3,4} |        | {5,3} | {5} | {4} | {3,4} | 0 | {4,3,5} |
| Panal dodecaédrico de orden 5 | {5,3,5} |        | {5,3} | {5} | {5} | {3,5} | 0 | Auto-dual |
También hay 11 panales H 3 paracompactos (aquellos con celdas (euclidianas) infinitas y/o figuras de vértice): {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} y {6,3,6}.
| Nombre | Símbolo de Schläfli {p,q,r} | Coxeter       | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de borde {r} | Figura de vértice {q,r} | χ | Dual |
|---|---|---|---|---|---|---|---|---|
| Panal tetraédrico de orden 6 | {3,3,6} |        | {3,3} | {3} | {6} | {3,6} | 0 | {6,3,3} |
| Panal de abeja con revestimiento hexagonal | {6,3,3} |        | {6,3} | {6} | {3} | {3,3} | 0 | {3,3,6} |
| Panal octaédrico de orden 4 | {3,4,4} |        | {3,4} | {3} | {4} | {4,4} | 0 | {4,4,3} |
| Azulejos cuadrados en forma de panal | {4,4,3} |        | {4,4} | {4} | {3} | {4,3} | 0 | {3,3,4} |
| Panal de abeja con teselación triangular | {3,6,3} |        | {3,6} | {3} | {3} | {6,3} | 0 | Auto-dual |
| Orden - 6 panales cúbicos | {4,3,6} |        | {4,3} | {4} | {4} | {3,6} | 0 | {6,3,4} |
| Orden-4 mosaico hexagonal panal | {6,3,4} |        | {6,3} | {6} | {4} | {3,4} | 0 | {4,3,6} |
| Orden - 4 baldosas cuadradas en forma de panal | {4,4,4} |        | {4,4} | {4} | {4} | {4,4} | 0 | Auto-dual |
| Panal dodecaédrico de orden 6 | {5,3,6} |        | {5,3} | {5} | {5} | {3,6} | 0 | {6,3,5} |
| Orden-5 mosaico hexagonal panal | {6,3,5} |        | {6,3} | {6} | {5} | {3,5} | 0 | {5,3,6} |
| Orden-6 mosaico hexagonal panal | {6,3,6} |        | {6,3} | {6} | {6} | {3,6} | 0 | Auto-dual |
Existen soluciones no compactas como grupos de Coxeter de Lorentz y se pueden visualizar con dominios abiertos en el espacio hiperbólico (el tetraedro fundamental tiene vértices ultraideales). Todos los panales con celdas hiperbólicas o figuras de vértices y que no tienen 2 en su símbolo de Schläfli son no compactos.
| { p ,3} \ r | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ... ∞ |
|---|---|---|---|---|---|---|---|---|
{2,3} |  {2,3,2} | {2,3,3} | {2,3,4} | {2,3,5} | {2,3,6} | {2,3,7} | {2,3,8} | {2,3,∞} |
{3,3} |  {3,3,2} |  {3,3,3} |  {3,3,4} |  {3,3,5} |  {3,3,6} |  {3,3,7} |  {3,3,8} |  {3,3,∞} |
{4,3} |  {4,3,2} |  {4,3,3} |  {4,3,4} |  {4,3,5} |  {4,3,6} |  {4,3,7} |  {4,3,8} |  {4,3,∞} |
{5,3} |  {5,3,2} |  {5,3,3} |  {5,3,4} |  {5,3,5} |  {5,3,6} |  {5,3,7} |  {5,3,8} |  {5,3,∞} |
{6,3} |  {6,3,2} |  {6,3,3} |  {6,3,4} |  {6,3,5} |  {6,3,6} |  {6,3,7} |  {6,3,8} |  {6,3,∞} |
{7,3} | {7,3,2} |  {7,3,3} |  {7,3,4} |  {7,3,5} |  {7,3,6} |  {7,3,7} |  {7,3,8} |  {7,3,∞} |
{8,3} | {8,3,2} |  {8,3,3} |  {8,3,4} |  {8,3,5} |  {8,3,6} |  {8,3,7} |  {8,3,8} |  {8,3,∞} |
... {∞,3} | {∞,3,2} |  {∞,3,3} |  {∞,3,4} |  {∞,3,5} |  {∞,3,6} |  {∞,3,7} |  {∞,3,8} |  {∞,3,∞} |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
En H 3 no hay panales estelares hiperbólicos regulares : todas las formas con un poliedro estrellado regular como celda, figura de vértice o ambas terminan siendo esféricas.
Los vértices ideales aparecen ahora cuando la figura del vértice es un mosaico euclidiano, que se vuelve inscribible en una horósfera en lugar de una esfera. Son duales a las celdas ideales (mosaicos euclidianos en lugar de poliedros finitos). A medida que el último número en el símbolo de Schläfli aumenta, la figura del vértice se vuelve hiperbólica y los vértices se vuelven ultra-ideales (por lo que las aristas no se encuentran dentro del espacio hiperbólico). En los panales {p, q, ∞} las aristas intersecan la bola de Poincaré solo en un punto ideal; el resto de la arista se ha vuelto ultra-ideal. Continuar más conduciría a aristas que son completamente ultra-ideales, tanto para el panal como para el símplex fundamental (aunque todavía infinitos {p, q} se encontrarían en tales aristas). En general, cuando el último número del símbolo de Schläfli se convierte en ∞, las caras de codimensión dos intersecan la hiperbola de Poincaré solo en un punto ideal. [16]
5-apeirotopos
Teselaciones del espacio 4 euclidiano
Hay tres tipos de teselaciones regulares infinitas ( panales ) que pueden teselar el espacio euclidiano de cuatro dimensiones:
| Nombre | Símbolo de Schläfli {p,q,r,s} | Tipo de faceta {p,q,r} | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de la cara {s} | Figura de borde {r,s} | Figura de vértice {q,r,s} | Dual |
|---|---|---|---|---|---|---|---|---|
| Panal teseractico | {4,3,3,4} | {4,3,3} | {4,3} | {4} | {4} | {3,4} | {3,3,4} | Auto-dual |
| Panal de abeja de 16 celdas | {3,3,4,3} | {3,3,4} | {3,3} | {3} | {3} | {4,3} | {3,4,3} | {3,4,3,3} |
| Panal de abeja de 24 celdas | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {3} | {3,3} | {4,3,3} | {3,3,4,3} |
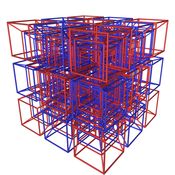 Porción proyectada de {4,3,3,4} (panal teseractico) | 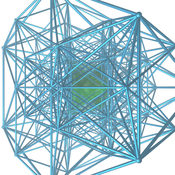 Porción proyectada de {3,3,4,3} (panal de 16 celdas) |  Porción proyectada de {3,4,3,3} (panal de 24 celdas) |
También existen los dos casos impropios {4,3,4,2} y {2,4,3,4}.
Hay tres panales planos regulares del 4-espacio euclidiano: [25]
- {4,3,3,4}, {3,3,4,3} y {3,4,3,3}.
Hay siete panales planos regulares convexos del 4-espacio hiperbólico: [18]
- 5 son compactos: {3,3,3,5}, {5,3,3,3}, {4,3,3,5}, {5,3,3,4}, {5,3,3,5}
- 2 son paracompactos: {3,4,3,4} y {4,3,4,3}.
Hay cuatro panales estelares regulares planos de 4-espacios hiperbólicos: [18]
- {5/2,5,3,3}, {3,3,5,5/2}, {3,5,5/2,5} y {5,5/2,5,3}.
Teselaciones del espacio hiperbólico 4-espacial
Hay siete panales regulares convexos y cuatro panales en forma de estrella en el espacio H 4 . [26] Cinco convexos son compactos y dos son paracompactos.
Cinco panales compactos regulares en H 4 :
| Nombre | Símbolo de Schläfli {p,q,r,s} | Tipo de faceta {p,q,r} | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de la cara {s} | Figura de borde {r,s} | Figura de vértice {q,r,s} | Dual |
|---|---|---|---|---|---|---|---|---|
| Orden 5 Panal de abeja de 5 celdas | {3,3,3,5} | {3,3,3} | {3,3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} |
| Panal de abeja de 120 celdas | {5,3,3,3} | {5,3,3} | {5,3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} |
| Orden-5 Panal teseractico | {4,3,3,5} | {4,3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3,3,4} |
| Orden 4 Panal de abeja de 120 celdas | {5,3,3,4} | {5,3,3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3,3,5} |
| Orden 5 Panal de abeja de 120 celdas | {5,3,3,5} | {5,3,3} | {5,3} | {5} | {5} | {3,5} | {3,3,5} | Auto-dual |
Los dos panales H 4 regulares paracompactos son: {3,4,3,4}, {4,3,4,3}.
| Nombre | Símbolo de Schläfli {p,q,r,s} | Tipo de faceta {p,q,r} | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de la cara {s} | Figura de borde {r,s} | Figura de vértice {q,r,s} | Dual |
|---|---|---|---|---|---|---|---|---|
| Orden 4 Panal de abeja de 24 celdas | {3,4,3,4} | {3,4,3} | {3,4} | {3} | {4} | {3,4} | {4,3,4} | {4,3,4,3} |
| Panal cúbico panal | {4,3,4,3} | {4,3,4} | {4,3} | {4} | {3} | {4,3} | {3,4,3} | {3,4,3,4} |
Existen soluciones no compactas como grupos de Coxeter de Lorentz y se pueden visualizar con dominios abiertos en el espacio hiperbólico (la celda 5 fundamental tiene algunas partes inaccesibles más allá del infinito). Todos los panales que no se muestran en el conjunto de tablas a continuación y que no tienen 2 en su símbolo de Schläfli son no compactos.
| Panales esféricos / euclidianos /hiperbólicos ( compactos / paracompactos / no compactos ) {p,q,r,s} | ||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
Teselaciones estelares del espacio hiperbólico 4-espacial
En el espacio H4 hay cuatro panales de abeja regulares , todos compactos:
| Nombre | Símbolo de Schläfli {p,q,r,s} | Tipo de faceta {p,q,r} | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de la cara {s} | Figura de borde {r,s} | Figura de vértice {q,r,s} | Dual | Densidad |
|---|---|---|---|---|---|---|---|---|---|
| Pequeño panal de abeja estrellado de 120 celdas | {5/2,5,3,3} | {5/2,5,3} | {5/2,5} | {5/2} | {3} | {3,3} | {5,3,3} | {3,3,5,5/2} | 5 |
| Panal de abeja de 600 celdas de orden pentagramático | {3,3,5,5/2} | {3,3,5} | {3,3} | {3} | {5/2} | {5,5/2} | {3,5,5/2} | {5/2,5,3,3} | 5 |
| Panal icosaédrico de 120 celdas, orden 5 | {3,5,5/2,5} | {3,5,5/2} | {3,5} | {3} | {5} | {5/2,5} | {5,5/2,5} | {5,5/2,5,3} | 10 |
| Gran panal de abeja de 120 celdas | {5,5/2,5,3} | {5,5/2,5} | {5,5/2} | {5} | {3} | {5,3} | {5/2,5,3} | {3,5,5/2,5} | 10 |
6-apeirotopos
Sólo hay un panal plano regular del espacio euclidiano 5: (anteriormente enumerados como teselaciones) [25]
- {4,3,3,3,4}
Hay cinco panales regulares planos de 5-espacio hiperbólico, todos paracompactos: (previamente enumerados arriba como teselaciones) [18]
- {3,3,3,4,3}, {3,4,3,3,3}, {3,3,4,3,3}, {3,4,3,3,4} y {4,3,3,4,3}
Teselaciones del espacio euclidiano 5
El panal hipercúbico es la única familia de panales regulares que pueden teselar cada dimensión, cinco o más, formada por facetas de hipercubo , cuatro alrededor de cada cresta .
| Nombre | Schläfli { pag 1 , pag 2 , ..., pag norte −1 } | Tipo de faceta | Figura de vértice | Dual |
|---|---|---|---|---|
| Azulejos cuadrados | {4,4} | {4} | {4} | Auto-dual |
| Panal cúbico | {4,3,4} | {4,3} | {3,4} | Auto-dual |
| Panal teseractico | {4,3 2 ,4} | {4,3 2 } | {3 2 ,4} | Auto-dual |
| Panal de abeja de 5 cubos | {4,3 3 ,4} | {4,3 3 } | {3 3 ,4} | Auto-dual |
| Panal de abeja de 6 cubos | {4,3 4 ,4} | {4,3 4 } | {3 4 ,4} | Auto-dual |
| Panal de abeja de 7 cubos | {4,3 5 ,4} | {4,3 5 } | {3 5 ,4} | Auto-dual |
| Panal de abeja de 8 cubos | {4,3 6 ,4} | {4,3 6 } | {3 6 ,4} | Auto-dual |
| n- panal hipercúbico | {4,3 n−2 ,4} | {4,3 n−2 } | {3 n−2 ,4} | Auto-dual |
En E 5 , también existen los casos impropios {4,3,3,4,2}, {2,4,3,3,4}, {3,3,4,3,2}, {2,3,3,4,3}, {3,4,3,3,2} y {2,3,4,3,3}. En E n , {4,3 n−3 ,4,2} y {2,4,3 n−3 ,4} son siempre teselaciones euclidianas impropias.
Teselaciones del espacio hiperbólico 5
Hay 5 panales regulares en H 5 , todos paracompactos, que incluyen infinitas facetas (euclidianas) o figuras de vértice: {3,4,3,3,3}, {3,3,4,3,3}, {3,3,3,4,3}, {3,4,3,3,4} y {4,3,3,4,3}.
No existen teselaciones regulares compactas del espacio hiperbólico de dimensión 5 o superior ni teselaciones regulares paracompactas en el espacio hiperbólico de dimensión 6 o superior.
| Nombre | Símbolo de Schläfli {p,q,r,s,t} | Tipo de faceta {p,q,r,s} | Tipo de 4 caras {p,q,r} | Tipo de célula {p,q} | Tipo de rostro {p} | Figura de celda {t} | Figura de la cara {s,t} | Figura de arista {r,s,t} | Figura de vértice {q,r,s,t} | Dual |
|---|---|---|---|---|---|---|---|---|---|---|
| Panal de abeja de 5 ortoplexes | {3,3,3,4,3} | {3,3,3,4} | {3,3,3} | {3,3} | {3} | {3} | {4,3} | {3,4,3} | {3,3,4,3} | {3,4,3,3,3} |
| Panal de abeja de 24 celdas | {3,4,3,3,3} | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {3} | {3,3} | {3,3,3} | {4,3,3,3} | {3,3,3,4,3} |
| Panal de abeja de 16 celdas | {3,3,4,3,3} | {3,3,4,3} | {3,3,4} | {3,3} | {3} | {3} | {3,3} | {4,3,3} | {3,4,3,3} | auto-dual |
| Orden-4 Panal de abeja de 24 celdas | {3,4,3,3,4} | {3,4,3,3} | {3,4,3} | {3,4} | {3} | {4} | {3,4} | {3,3,4} | {4,3,3,4} | {4,3,3,4,3} |
| Panal de abeja teseractico | {4,3,3,4,3} | {4,3,3,4} | {4,3,3} | {4,3} | {4} | {3} | {4,3} | {3,4,3} | {3,3,4,3} | {3,4,3,3,4} |
Dado que no hay n -politopos estelares regulares para n ≥ 5, que podrían ser celdas potenciales o figuras de vértice, ya no hay más panales estelares hiperbólicos en H n para n ≥ 5.
Apeirotopos de rango 7 o más
Teselaciones de hiperbólicos de 6 espacios y superiores
No existen teselaciones regulares compactas o paracompactas del espacio hiperbólico de dimensión 6 o superior. Sin embargo, cualquier símbolo de Schläfli de la forma {p,q,r,s,...} no contemplado anteriormente (p,q,r,s,... números naturales superiores a 2, o infinito) formará una teselación no compacta del espacio n hiperbólico . [16]
Politopos abstractos
Los politopos abstractos surgieron de un intento de estudiar los politopos aparte del espacio geométrico en el que están insertos. Incluyen las teselaciones del espacio esférico, euclidiano e hiperbólico, y de otras variedades . Hay una cantidad infinita de cada rango mayor que 1. Consulte este atlas para ver una muestra. Algunos ejemplos notables de politopos regulares abstractos que no aparecen en ninguna otra parte de esta lista son el poliedro de 11 celdas , {3,5,3}, y el poliedro de 57 celdas , {5,3,5}, que tienen poliedros proyectivos regulares como celdas y figuras de vértice.
Los elementos de un poliedro abstracto son su cuerpo (el elemento máximo), sus caras, aristas, vértices y el politopo nulo o conjunto vacío. Estos elementos abstractos pueden ser mapeados en el espacio ordinario o realizados como figuras geométricas. Algunos poliedros abstractos tienen realizaciones bien formadas o fieles , otros no. Una bandera es un conjunto conexo de elementos de cada rango - para un poliedro, esto es el cuerpo, una cara, una arista de la cara, un vértice de la arista y el politopo nulo. Se dice que un politopo abstracto es regular si sus simetrías combinatorias son transitivas en sus banderas - es decir, que cualquier bandera puede ser mapeada en cualquier otra bajo una simetría del poliedro. Los politopos abstractos regulares siguen siendo un área activa de investigación.
Cinco de estos poliedros abstractos regulares, que no pueden realizarse de forma fiel y simétrica, fueron identificados por HSM Coxeter en su libro Regular Polytopes (1977) y nuevamente por JM Wills en su artículo "The combinatorially regular polyhedra of index 2" (1987). [27] Todos ellos son topológicamente equivalentes a los toroides . Su construcción, al disponer n caras alrededor de cada vértice, puede repetirse indefinidamente como teselas del plano hiperbólico . En los diagramas siguientes, las imágenes de teselas hiperbólicas tienen colores correspondientes a los de las imágenes de poliedros.
Poliedro 
Triacontaedro rómbico medial
Dodecadodecaedro
Icosaedro triámbico medial
Dodecadodecaedro ditrigonal
Dodecaedro excavadoFigura de vértice {5}, {5/2} 

(5,5/2) 2 
{5}, {5/2} 

(5,5/3) 3 

Caras 30 rombos 
12 pentágonos
12 pentagramas

20 hexágonos 
12 pentágonos
12 pentagramas

20 hexagramas 
Embaldosado 
{4, 5}
{5, 4}
{6, 5}
{5, 6}
{6, 6}χ -6 -6 -16 -16 -20
Estos se presentan como pares duales de la siguiente manera:
- El triacontaedro rómbico medial y el dodecadodecaedro son duales entre sí.
- El icosaedro triámbico medial y el dodecadodecaedro ditrigonal son duales entre sí.
- El dodecaedro excavado es autodual.
Véase también
- Lista de compuestos politópicos regulares
- Polígono
- Poliedro
- Poliedro regular (5 sólidos platónicos regulares y 4 sólidos de Kepler-Poinsot )
- Petrial
- 4-politopo
- 4 politopos regulares (16 4 politopos regulares, 4 convexos y 10 estrellas (Schläfli – Hess))
- Politopo 4 uniforme
- Mosaico
- Politopo regular
- Mapa regular (teoría de grafos)
Notas
- ^ (hasta identidad e idempotencia)
- ^ En una clasificación propuesta por Conway y adoptada por Coxeter , [a] la estelación se refiere a la extensión de los bordes, y el agrandamiento a la extensión de las caras; el término agrandamiento se da para la extensión de las células (de polychora), aunque parece ser menos comúnmente usado. [b]
Subnotas
- ^ Coxeter, HMS (1975). Politopos complejos regulares (1.ª ed.). Cambridge University Press. pp. 46-7. ISBN 9780521201254.
- ^ Véase: Inchbald, Guy (9 de septiembre de 2024). «Estelación y facetado: una breve historia». Página de Guy sobre poliedros . Archivado desde el original el 20 de mayo de 2024.
Referencias
- ^ ab McMullen, Peter (2004), "Polítopos regulares de rango completo", Geometría discreta y computacional , 32 : 1–35, doi :10.1007/s00454-004-0848-5, S2CID 46707382
- ^ Coxeter (1973), pág. 129.
- ^ McMullen y Schulte (2002), pág. 30.
- ^ Johnson, NW (2018). "Capítulo 11: Grupos de simetría finitos". Geometrías y transformaciones . Cambridge University Press. 11.1 Politopos y panales, pág. 224. ISBN 978-1-107-10340-5.
- ^ Coxeter (1973), pág. 120.
- ^ Coxeter (1973), pág. 124.
- ^ Coxeter, Politopos complejos regulares , pág. 9
- ^ Duncan, Hugh (28 de septiembre de 2017). "Entre una roca cuadrada y un pentágono duro: polígonos fraccionarios". polvo de tiza .
- ^ desde McMullen y Schulte 2002.
- ^ Coxeter (1973), págs. 66-67.
- ^ Resúmenes (PDF) . Polytopes convexos y abstractos (19-21 de mayo de 2005) y Día de los politopos en Calgary (22 de mayo de 2005).
- ^ McMullen (2004).
- ^ Coxeter (1973), Tabla I: Politopos regulares, (iii) Los tres politopos regulares en n dimensiones (n>=5), págs. 294–295.
- ^ McMullen y Schulte (2002), "Politopos regulares proyectivos 6C", págs. 162-165.
- ^ Grünbaum, B. (1977). "Poliedros regulares: antiguos y nuevos". Aecuaciones Mathematicae . 16 (1–2): 1–20. doi :10.1007/BF01836414. S2CID 125049930.
- ^ abc Roice Nelson y Henry Segerman, Visualización de panales hiperbólicos
- ^ Irving Adler, Una nueva mirada a la geometría (edición Dover de 2012), pág. 233
- ^ abcde Coxeter (1999), "Capítulo 10".
- ^ Coxeter, HSM (1938). "Poliedros regulares oblicuos en tres y cuatro dimensiones". Proc. London Math. Soc . 2. 43 : 33–62. doi :10.1112/plms/s2-43.1.33.
- ^ Coxeter, HSM (1985). "Politopos regulares y semirregulares II". Mathematische Zeitschrift . 188 (4): 559–591. doi :10.1007/BF01161657. S2CID 120429557.
- ^ Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "Capítulo 23: Objetos con simetría primaria, poliedros platónicos infinitos". Las simetrías de las cosas . Taylor & Francis. págs. 333–335. ISBN 978-1-568-81220-5.
- ^ McMullen y Schulte (2002), pág. 224.
- ^ McMullen y Schulte (2002), Sección 7E.
- ^ Garner, CWL (1967). "Poliedros regulares oblicuos en el espacio tridimensional hiperbólico". Can. J. Math . 19 : 1179–1186. doi : 10.4153/CJM-1967-106-9 . S2CID : 124086497.Nota: Su artículo dice que hay 32, pero uno es auto-dual, quedando 31.
- ^ abc Coxeter (1973), Tabla II: Panales regulares, pág. 296.
- ^ Coxeter (1999), "Capítulo 10", Tabla IV, pág. 213.
- ^ David A. Richter. «Los poliedros regulares (de índice dos)». Archivado desde el original el 4 de marzo de 2016. Consultado el 13 de marzo de 2015 .
Citas
- Coxeter, HSM (1999), "Capítulo 10: Panales regulares en el espacio hiperbólico", La belleza de la geometría: doce ensayos , Mineola, NY: Dover Publications, Inc., págs. 199–214, ISBN 0-486-40919-8, LCCN 99035678, MR 1717154. Véanse en particular los cuadros resumen II, III, IV, V, págs. 212-213.
- Publicado originalmente en Coxeter, HSM (1956), "Regular honeycombs in hyperbolic space" (PDF) , Actas del Congreso Internacional de Matemáticos, 1954, Ámsterdam , vol. III, Ámsterdam: North-Holland Publishing Co., págs. 155–169, MR 0087114, archivado desde el original (PDF) el 2 de abril de 2015.
- Coxeter, HSM (1973) [1948]. Politopos regulares (tercera edición). Nueva York: Dover Publications. ISBN 0-486-61480-8. Sr. 0370327. OCLC 798003.Véanse en particular las Tablas I y II: Politopos regulares y panales, págs. 294-296.
- Johnson, Norman W. (2012), "Polítopos regulares inversos" (PDF) , Conferencia internacional sobre matemáticas de distancias y aplicaciones (2 al 5 de julio de 2012, Varna, Bulgaria) , págs. 85-95, documento 27
- McMullen, Peter ; Schulte, Egon (2002), Politopos regulares abstractos , Enciclopedia de matemáticas y sus aplicaciones, vol. 92, Cambridge: Cambridge University Press, doi :10.1017/CBO9780511546686, ISBN 0-521-81496-0, Sr. 1965665, S2CID 115688843
- McMullen, Peter (2018), "Nuevos compuestos regulares de 4-politopos", Nuevas tendencias en geometría intuitiva , Bolyai Society Mathematical Studies, vol. 27, págs. 307–320, doi :10.1007/978-3-662-57413-3_12, ISBN 978-3-662-57412-6.
- Nelson, Roice; Segerman, Henry (2015). "Visualización de panales hiperbólicos". arXiv : 1511.02851 [math.HO].hiperbolichoneycombs.org/
- Sommerville, DMY (1958), Introducción a la geometría de n dimensiones , Nueva York: Dover Publications, Inc., MR 0100239Reimpresión de la edición de 1930, publicada por EP Dutton. Véase en particular el Capítulo X: Los politopos regulares.
Enlaces externos
- Los sólidos platónicos
- Poliedros de Kepler-Poinsot
- Desplegables de politopos 4d regulares
- Glosario multidimensional (busque Hexacosichoron y Hecatonicosachoron)
- Visor de politopos
- Politopos y empaquetamiento óptimo de p puntos en esferas n-dimensionales
- Atlas de pequeños politopos regulares
- Poliedros regulares a través del tiempo I. Hubard, Politopos, Mapas y sus Simetrías
- Politopos de estrellas regulares, Nan Ma
| Espacio | Familia | / / | ||||
|---|---|---|---|---|---|---|
| Y 2 | Azulejos uniformes | 0 [3] | delta 3 | hδ3 | qδ3 | Hexagonal |
| Y 3 | Panal de abeja convexo uniforme | 0 [4] | delta 4 | hδ4 | qδ4 | |
| E4 | Uniforme de 4 panales | 0 [5] | del 5 | hδ5 | qδ5 | Panal de abeja de 24 celdas |
| E 5 | Uniforme de 5 panales | 0 [6] | delta 6 | hδ6 | qδ6 | |
| E6 | Uniforme de 6 panales | 0 [7] | delta 7 | hδ7 | qδ7 | 2 22 |
| E7 | Uniforme de 7 panales | 0 [8] | del 8 | hδ8 | qδ8 | 1 33 • 3 31 |
| E8 | Uniforme de 8 panales | 0 [9] | del 9 | hδ9 | qδ9 | 1 52 • 2 51 • 5 21 |
| E9 | Uniforme de 9 panales | 0 [10] | delta 10 | hδ10 | qδ10 | |
| E10 | Uniforme de 10 panales | 0 [11] | delta 11 | hδ11 | qδ11 | |
| En -1 | Uniforme ( n -1)- panal | 0 [ n ] | delta n | hδn | qδn | 1 k2 • 2 k1 • k21 |







































![{\displaystyle {\begin{aligned}&{\frac {1}{p}}+{\frac {1}{q}}>{\frac {1}{2}}:{\text{Poliedro (existente en el espacio tridimensional euclidiano)}}\\[6pt]&{\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}:{\text{Teselación del plano euclidiano}}\\[6pt]&{\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}:{\text{Teselación del plano hiperbólico}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b3e3112344f5e050eb160928c5170cabb51bcf8)




































































































































































































































