Magnetismo
.jpg/440px-Metal_shavings_around_bar_magnet_(close-up).jpg)
| Artículos sobre |
| Electromagnetismo |
|---|
 |
El magnetismo es la clase de atributos físicos que se producen a través de un campo magnético , que permite que los objetos se atraigan o se repelan entre sí. Debido a que tanto las corrientes eléctricas como los momentos magnéticos de las partículas elementales dan lugar a un campo magnético, el magnetismo es uno de los dos aspectos del electromagnetismo .
Los efectos más conocidos se producen en materiales ferromagnéticos , que son fuertemente atraídos por los campos magnéticos y pueden magnetizarse para convertirse en imanes permanentes , produciendo ellos mismos campos magnéticos. También es posible desmagnetizar un imán. Solo unas pocas sustancias son ferromagnéticas; las más comunes son el hierro , el cobalto , el níquel y sus aleaciones.
Todas las sustancias exhiben algún tipo de magnetismo. Los materiales magnéticos se clasifican según su susceptibilidad en masa. [1] El ferromagnetismo es responsable de la mayoría de los efectos del magnetismo que se encuentran en la vida cotidiana, pero en realidad hay varios tipos de magnetismo. Las sustancias paramagnéticas , como el aluminio y el oxígeno , son débilmente atraídas por un campo magnético aplicado; las sustancias diamagnéticas , como el cobre y el carbono , son débilmente repelidas; mientras que los materiales antiferromagnéticos , como el cromo , tienen una relación más compleja con un campo magnético. [ vago ] La fuerza de un imán sobre materiales paramagnéticos, diamagnéticos y antiferromagnéticos suele ser demasiado débil para ser sentida y solo puede detectarse con instrumentos de laboratorio, por lo que en la vida cotidiana, estas sustancias a menudo se describen como no magnéticas.
La intensidad de un campo magnético siempre disminuye con la distancia a la fuente magnética, [2] aunque la relación matemática exacta entre intensidad y distancia varía. Muchos factores pueden influir en el campo magnético de un objeto, entre ellos el momento magnético del material, la forma física del objeto, tanto la magnitud como la dirección de cualquier corriente eléctrica presente en el objeto y la temperatura del objeto.
Historia
This section needs additional citations for verification. (October 2024) |



El magnetismo se descubrió por primera vez en el mundo antiguo cuando la gente notó que las piedras imán , piezas magnetizadas naturalmente del mineral magnetita , podían atraer el hierro. [3] La palabra imán proviene del término griego μαγνῆτις λίθος magnētis lithos , [4] "la piedra de magnesio, piedra imán". [5] En la antigua Grecia, Aristóteles atribuyó la primera de lo que podría llamarse una discusión científica del magnetismo al filósofo Tales de Mileto , que vivió desde aproximadamente el 625 a. C. hasta aproximadamente el 545 a. C. [6] El antiguo texto médico indio Sushruta Samhita describe el uso de magnetita para eliminar flechas incrustadas en el cuerpo de una persona. [7]
En la antigua China , la primera referencia literaria al magnetismo se encuentra en un libro del siglo IV a. C. que lleva el nombre de su autor, Guiguzi . [8] Los anales del siglo II a. C., Lüshi Chunqiu , también señalan: "La piedra imán hace que el hierro se acerque; alguna (fuerza) lo atrae". [9] La primera mención de la atracción de una aguja se encuentra en una obra del siglo I Lunheng ( Investigaciones equilibradas ): "Una piedra imán atrae una aguja". [10] El científico chino del siglo XI Shen Kuo fue la primera persona en escribir, en los Ensayos del estanque de los sueños , sobre la brújula de aguja magnética y que mejoró la precisión de la navegación al emplear el concepto astronómico del norte verdadero . En el siglo XII, se sabía que los chinos usaban la brújula de piedra imán para la navegación. Esculpieron una cuchara direccional a partir de piedra imán de tal manera que el mango de la cuchara siempre apuntara al sur.
En 1187, Alexander Neckam fue el primero en Europa en describir la brújula y su uso para la navegación. En 1269, Peter Peregrinus de Maricourt escribió la Epistola de magnete , el primer tratado existente que describe las propiedades de los imanes. En 1282, Al-Ashraf Umar II , un físico , astrónomo y geógrafo yemení, analizó las propiedades de los imanes y las brújulas secas . [11]
La única obra existente de Leonardo Garzoni , los Dos tratados sobre la naturaleza y las cualidades del imán , es el primer ejemplo conocido de un tratamiento moderno de los fenómenos magnéticos. Escrito en los años cercanos a 1580 y nunca publicado, el tratado tuvo una amplia difusión. En particular, Garzoni es mencionado como un experto en magnetismo por Niccolò Cabeo, cuya Philosophia Magnetica (1629) es simplemente un reajuste de la obra de Garzoni. El tratado de Garzoni también era conocido por Giovanni Battista Della Porta .
En 1600, William Gilbert publicó su obra De Magnete, Magneticisque Corporibus, et de Magno Magnete Tellure ( Sobre el imán y los cuerpos magnéticos, y sobre el gran imán que es la Tierra ). En esta obra describe muchos de sus experimentos con su modelo de tierra llamado terrella . A partir de sus experimentos, concluyó que la Tierra en sí era magnética y que esta era la razón por la que las brújulas apuntaban hacia el norte, mientras que, anteriormente, algunos creían que era la estrella polar Polaris o una gran isla magnética en el polo norte lo que atraía a la brújula.
La comprensión de la relación entre la electricidad y el magnetismo comenzó en 1819 con el trabajo de Hans Christian Ørsted , un profesor de la Universidad de Copenhague, quien descubrió, por el movimiento accidental de la aguja de una brújula cerca de un cable, que una corriente eléctrica podía crear un campo magnético. Este experimento histórico se conoce como el Experimento de Ørsted. Jean-Baptiste Biot y Félix Savart , quienes en 1820 idearon la ley de Biot-Savart que proporciona una ecuación para el campo magnético de un cable portador de corriente. Casi al mismo tiempo, André-Marie Ampère llevó a cabo numerosos experimentos sistemáticos y descubrió que la fuerza magnética entre dos bucles de corriente continua de cualquier forma es igual a la suma de las fuerzas individuales que cada elemento de corriente de un circuito ejerce sobre cada uno de los demás elementos de corriente del otro circuito.
En 1831, Michael Faraday descubrió que un flujo magnético variable en el tiempo induce un voltaje a través de un bucle de alambre. En 1835, Carl Friedrich Gauss planteó la hipótesis, basándose en la ley de fuerza de Ampère en su forma original, de que todas las formas de magnetismo surgen como resultado de cargas puntuales elementales que se mueven unas respecto de otras. [12] Wilhelm Eduard Weber adelantó la teoría de Gauss a la electrodinámica de Weber .
A partir de 1861, James Clerk Maxwell sintetizó y amplió muchos de estos conocimientos en las ecuaciones de Maxwell , unificando la electricidad, el magnetismo y la óptica en el campo del electromagnetismo . Sin embargo, la interpretación de Gauss del magnetismo no es totalmente compatible con la electrodinámica de Maxwell. En 1905, Albert Einstein utilizó las ecuaciones de Maxwell para motivar su teoría de la relatividad especial , [13] exigiendo que las leyes fueran ciertas en todos los marcos de referencia inerciales . El enfoque de Gauss de interpretar la fuerza magnética como un mero efecto de las velocidades relativas encontró así su camino de regreso a la electrodinámica en cierta medida.
El electromagnetismo ha seguido desarrollándose hasta el siglo XXI, incorporándose a las teorías más fundamentales de la teoría de calibre , la electrodinámica cuántica , la teoría electrodébil y, finalmente, el modelo estándar .
Fuentes
El magnetismo, en su raíz, surge de tres fuentes:
- Corriente eléctrica
- Momentos magnéticos de espín de partículas elementales
- Cambios en los campos eléctricos
Las propiedades magnéticas de los materiales se deben principalmente a los momentos magnéticos de los electrones que orbitan alrededor de sus átomos . Los momentos magnéticos de los núcleos de los átomos son típicamente miles de veces más pequeños que los momentos magnéticos de los electrones, por lo que son despreciables en el contexto de la magnetización de los materiales. Sin embargo, los momentos magnéticos nucleares son muy importantes en otros contextos, en particular en la resonancia magnética nuclear (RMN) y la resonancia magnética nuclear (RMN).
Por lo general, la enorme cantidad de electrones de un material se organiza de tal manera que sus momentos magnéticos (tanto orbitales como intrínsecos) se cancelan. Esto se debe, en cierta medida, a que los electrones se combinan en pares con momentos magnéticos intrínsecos opuestos como resultado del principio de exclusión de Pauli (ver configuración electrónica ), y se combinan en subcapas llenas con movimiento orbital neto cero. En ambos casos, los electrones adoptan preferentemente disposiciones en las que el momento magnético de cada electrón se cancela por el momento opuesto de otro electrón. Además, incluso cuando la configuración electrónica es tal que hay electrones desapareados y/o subcapas no llenas, a menudo ocurre que los diversos electrones en el sólido contribuirán con momentos magnéticos que apuntan en direcciones diferentes y aleatorias, de modo que el material no será magnético.
A veces, ya sea de manera espontánea o debido a un campo magnético externo aplicado, cada uno de los momentos magnéticos de los electrones estará, en promedio, alineado. Un material adecuado puede entonces producir un campo magnético neto intenso.
El comportamiento magnético de un material depende de su estructura, en particular de su configuración electrónica , por las razones mencionadas anteriormente, y también de la temperatura. A altas temperaturas, el movimiento térmico aleatorio hace que sea más difícil que los electrones mantengan la alineación.
Tipos

Diamagnetismo
El diamagnetismo aparece en todos los materiales y es la tendencia de un material a oponerse a un campo magnético aplicado y, por lo tanto, a ser repelido por un campo magnético. Sin embargo, en un material con propiedades paramagnéticas (es decir, con tendencia a potenciar un campo magnético externo), predomina el comportamiento paramagnético. [15] Por lo tanto, a pesar de su ocurrencia universal, el comportamiento diamagnético se observa solo en un material puramente diamagnético. En un material diamagnético, no hay electrones desapareados, por lo que los momentos magnéticos intrínsecos de los electrones no pueden producir ningún efecto de volumen. En estos casos, la magnetización surge de los movimientos orbitales de los electrones, que pueden entenderse clásicamente de la siguiente manera:
Cuando un material se coloca en un campo magnético, los electrones que giran alrededor del núcleo experimentarán, además de su atracción de Coulomb hacia el núcleo, una fuerza de Lorentz del campo magnético. Dependiendo de la dirección en la que orbite el electrón, esta fuerza puede aumentar la fuerza centrípeta sobre los electrones, atrayéndolos hacia el núcleo, o puede disminuir la fuerza, alejándolos del núcleo. Este efecto aumenta sistemáticamente los momentos magnéticos orbitales que estaban alineados en sentido opuesto al campo y disminuye los que estaban alineados en sentido paralelo al campo (de acuerdo con la ley de Lenz ). Esto da como resultado un pequeño momento magnético en masa, con una dirección opuesta al campo aplicado.
Esta descripción pretende ser únicamente una heurística ; el teorema de Bohr-Van Leeuwen demuestra que el diamagnetismo es imposible según la física clásica y que para comprenderlo adecuadamente se necesita una descripción mecánico-cuántica .
Todos los materiales experimentan esta respuesta orbital. Sin embargo, en las sustancias paramagnéticas y ferromagnéticas, el efecto diamagnético se ve superado por los efectos mucho más fuertes provocados por los electrones desapareados.
Paramagnetismo
En un material paramagnético hay electrones desapareados, es decir, orbitales atómicos o moleculares con exactamente un electrón en ellos. Mientras que el principio de exclusión de Pauli exige que los electrones apareados tengan sus momentos magnéticos intrínsecos ('spin') apuntando en direcciones opuestas, lo que hace que sus campos magnéticos se cancelen, un electrón desapareado es libre de alinear su momento magnético en cualquier dirección. Cuando se aplica un campo magnético externo, estos momentos magnéticos tenderán a alinearse en la misma dirección que el campo aplicado, reforzándolo así.
Ferromagnetismo
Un ferroimán, al igual que una sustancia paramagnética, tiene electrones desapareados. Sin embargo, además de la tendencia del momento magnético intrínseco de los electrones a ser paralelo a un campo aplicado, también existe en estos materiales una tendencia a que estos momentos magnéticos se orienten en paralelo entre sí para mantener un estado de energía reducida. Por lo tanto, incluso en ausencia de un campo aplicado, los momentos magnéticos de los electrones en el material se alinean espontáneamente en paralelo entre sí.
Cada sustancia ferromagnética tiene su propia temperatura individual, llamada temperatura de Curie o punto de Curie, por encima de la cual pierde sus propiedades ferromagnéticas. Esto se debe a que la tendencia térmica al desorden supera la disminución de energía debida al orden ferromagnético.
El ferromagnetismo sólo ocurre en unas pocas sustancias; las más comunes son el hierro , el níquel , el cobalto , sus aleaciones y algunas aleaciones de metales de tierras raras .
Dominios magnéticos
Los momentos magnéticos de los átomos en un material ferromagnético hacen que se comporten como pequeños imanes permanentes. Se adhieren entre sí y se alinean en pequeñas regiones de alineación más o menos uniforme llamadas dominios magnéticos o dominios de Weiss . Los dominios magnéticos se pueden observar con un microscopio de fuerza magnética para revelar límites de dominios magnéticos que se parecen a líneas blancas en el dibujo. Hay muchos experimentos científicos que pueden mostrar físicamente los campos magnéticos.
Cuando un dominio contiene demasiadas moléculas, se vuelve inestable y se divide en dos dominios alineados en direcciones opuestas para que se adhieran entre sí de forma más estable.
Cuando se exponen a un campo magnético, los límites de los dominios se mueven, de modo que los dominios alineados con el campo magnético crecen y dominan la estructura (área amarilla punteada), como se muestra a la izquierda. Cuando se elimina el campo magnético, los dominios pueden no volver a un estado no magnetizado. Esto hace que el material ferromagnético se magnetice y forme un imán permanente.
Cuando se magnetiza con la suficiente fuerza como para que el dominio predominante invada a todos los demás y dé como resultado un solo dominio, el material está saturado magnéticamente . Cuando un material ferromagnético magnetizado se calienta hasta la temperatura del punto de Curie , las moléculas se agitan hasta el punto en que los dominios magnéticos pierden la organización y las propiedades magnéticas que causan cesan. Cuando el material se enfría, esta estructura de alineación de dominios regresa espontáneamente, de una manera aproximadamente análoga a cómo un líquido puede congelarse y convertirse en un sólido cristalino.
Antiferromagnetismo
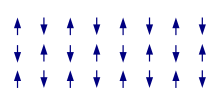
En un antiferroimán , a diferencia de un ferroimán, existe una tendencia a que los momentos magnéticos intrínsecos de los electrones de valencia vecinos apunten en direcciones opuestas . Cuando todos los átomos están dispuestos en una sustancia de modo que cada vecino sea antiparalelo, la sustancia es antiferromagnética . Los antiferroimanes tienen un momento magnético neto cero porque el momento opuesto adyacente se cancela, lo que significa que no producen ningún campo. Los antiferroimanes son menos comunes en comparación con los otros tipos de comportamientos y se observan principalmente a bajas temperaturas. A temperaturas variables, se puede observar que los antiferroimanes exhiben propiedades diamagnéticas y ferromagnéticas.
En algunos materiales, los electrones vecinos prefieren apuntar en direcciones opuestas, pero no existe una disposición geométrica en la que cada par de vecinos esté antialineado. Esto se denomina antiferromagnético inclinado o hielo de espín y es un ejemplo de frustración geométrica .
Ferrimagnetismo
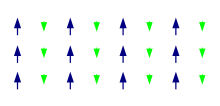
Al igual que el ferromagnetismo, los ferroimanes conservan su magnetización en ausencia de un campo. Sin embargo, al igual que los antiferroimanes, los pares vecinos de espines de electrones tienden a apuntar en direcciones opuestas. Estas dos propiedades no son contradictorias, porque en la disposición geométrica óptima, hay más momento magnético de la subred de electrones que apuntan en una dirección, que de la subred que apunta en la dirección opuesta.
La mayoría de las ferritas son ferromagnéticas. La primera sustancia magnética descubierta, la magnetita , es una ferrita y en un principio se creyó que era un ferroimán; sin embargo, Louis Néel desmintió esta teoría tras descubrir el ferromagnetismo.
Superparamagnetismo
Cuando un ferroimán o ferriimán es suficientemente pequeño, actúa como un único espín magnético sujeto a un movimiento browniano . Su respuesta a un campo magnético es cualitativamente similar a la respuesta de un paraimán, pero mucho mayor.
Magnetismo de Nagaoka
El físico japonés Yosuke Nagaoka ideó un tipo de magnetismo en una red cuadrada bidimensional en la que cada nodo de la red tenía un electrón. Si se eliminaba un electrón en determinadas condiciones, la energía de la red sería mínima solo cuando los espines de todos los electrones fueran paralelos.
Experimentalmente se logró una variación de este método organizando los átomos en una red triangular de moiré de monocapas de diseluro de molibdeno y disulfuro de tungsteno . La aplicación de un campo magnético débil y un voltaje condujo a un comportamiento ferromagnético cuando había entre un 100 y un 150 % más de electrones que nodos de la red. Los electrones adicionales se deslocalizaron y se aparearon con los electrones de la red para formar doblones. La deslocalización se impidió a menos que los electrones de la red tuvieran espines alineados. De este modo, los doblones crearon regiones ferromagnéticas localizadas. El fenómeno tuvo lugar a 140 milikelvins. [16]
Otros tipos de magnetismo
Electroimán
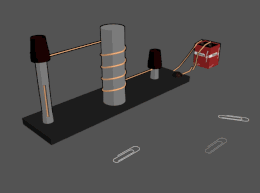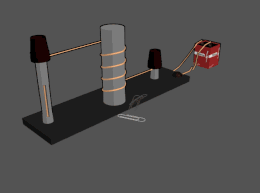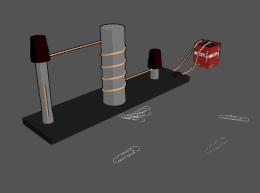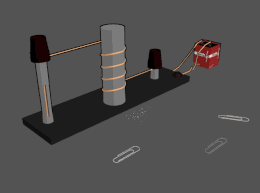
Un electroimán es un tipo de imán en el que el campo magnético es producido por una corriente eléctrica . [17] El campo magnético desaparece cuando se corta la corriente. Los electroimanes suelen constar de una gran cantidad de vueltas de cable muy espaciadas que crean el campo magnético. Las vueltas de cable suelen estar enrolladas alrededor de un núcleo magnético hecho de un material ferromagnético o ferromagnético como el hierro ; el núcleo magnético concentra el flujo magnético y crea un imán más potente.
La principal ventaja de un electroimán con respecto a un imán permanente es que el campo magnético se puede modificar rápidamente controlando la cantidad de corriente eléctrica en el bobinado. Sin embargo, a diferencia de un imán permanente que no necesita energía, un electroimán requiere un suministro continuo de corriente para mantener el campo magnético.
Los electroimanes se utilizan ampliamente como componentes de otros dispositivos eléctricos, como motores , generadores , relés , solenoides, altavoces , discos duros , máquinas de resonancia magnética , instrumentos científicos y equipos de separación magnética . Los electroimanes también se emplean en la industria para levantar y mover objetos de hierro pesados, como chatarra y acero. [18] El electromagnetismo se descubrió en 1820. [19]
Magnetismo, electricidad y relatividad especial
Como consecuencia de la teoría de la relatividad especial de Einstein , la electricidad y el magnetismo están fundamentalmente interrelacionados. Tanto el magnetismo sin electricidad como la electricidad sin magnetismo son incompatibles con la relatividad especial, debido a efectos como la contracción de la longitud , la dilatación del tiempo y el hecho de que la fuerza magnética depende de la velocidad. Sin embargo, cuando se tienen en cuenta tanto la electricidad como el magnetismo, la teoría resultante ( electromagnetismo ) es totalmente coherente con la relatividad especial. [13] [20] En particular, un fenómeno que parece puramente eléctrico o puramente magnético para un observador puede ser una mezcla de ambos para otro, o más generalmente las contribuciones relativas de la electricidad y el magnetismo dependen del marco de referencia. Así, la relatividad especial "mezcla" la electricidad y el magnetismo en un fenómeno único e inseparable llamado electromagnetismo , de forma análoga a cómo la relatividad general "mezcla" el espacio y el tiempo en el espacio-tiempo .
Todas las observaciones sobre el electromagnetismo se aplican a lo que podría considerarse principalmente magnetismo, por ejemplo, las perturbaciones en el campo magnético están necesariamente acompañadas por un campo eléctrico distinto de cero y se propagan a la velocidad de la luz . [21]
Campos magnéticos en un material
En el vacío,
donde μ 0 es la permeabilidad al vacío .
En un material,
La cantidad μ 0 M se llama polarización magnética .
Si el campo H es pequeño, la respuesta de la magnetización M en un diaimán o paraimán es aproximadamente lineal:
La constante de proporcionalidad se denomina susceptibilidad magnética. Si es así,
En un imán duro como un ferroimán, M no es proporcional al campo y generalmente no es cero incluso cuando H es cero (ver Remanencia ).
Fuerza magnética

El fenómeno del magnetismo está "mediado" por el campo magnético. Una corriente eléctrica o un dipolo magnético crea un campo magnético y ese campo, a su vez, imparte fuerzas magnéticas sobre otras partículas que se encuentran en el campo.
Las ecuaciones de Maxwell, que se simplifican en la ley de Biot-Savart en el caso de corrientes constantes, describen el origen y el comportamiento de los campos que gobiernan estas fuerzas. Por lo tanto, el magnetismo se observa siempre que las partículas cargadas eléctricamente están en movimiento , por ejemplo, a partir del movimiento de electrones en una corriente eléctrica o, en ciertos casos, a partir del movimiento orbital de los electrones alrededor del núcleo de un átomo. También surgen de dipolos magnéticos "intrínsecos" que surgen del espín mecánico cuántico .
Las mismas situaciones que crean campos magnéticos (carga en movimiento en una corriente o en un átomo y dipolos magnéticos intrínsecos) son también las situaciones en las que un campo magnético tiene un efecto, creando una fuerza. A continuación se muestra la fórmula para la carga en movimiento; para las fuerzas sobre un dipolo intrínseco, véase dipolo magnético.
Cuando una partícula cargada se mueve a través de un campo magnético B , siente una fuerza de Lorentz F dada por el producto vectorial : [22]
dónde
- es la carga eléctrica de la partícula, y
- v es el vector de velocidad de la partícula
Como se trata de un producto vectorial, la fuerza es perpendicular tanto al movimiento de la partícula como al campo magnético. De ello se deduce que la fuerza magnética no realiza trabajo sobre la partícula; puede cambiar la dirección del movimiento de la partícula, pero no puede hacer que se acelere o desacelere. La magnitud de la fuerza es
¿Dónde está el ángulo entre v y B ?
Una herramienta para determinar la dirección del vector de velocidad de una carga en movimiento, el campo magnético y la fuerza ejercida es etiquetar el dedo índice como "V" [ dudoso – discutir ] , el dedo medio como "B" y el pulgar como "F" con la mano derecha. Al hacer una configuración similar a la de una pistola, con el dedo medio cruzado debajo del dedo índice, los dedos representan el vector de velocidad, el vector de campo magnético y el vector de fuerza, respectivamente. Ver también la regla de la mano derecha .
Dipolos magnéticos
Una fuente muy común de campo magnético que se encuentra en la naturaleza es un dipolo , con un " polo sur " y un " polo norte ", términos que se remontan al uso de imanes como brújulas, que interactúan con el campo magnético de la Tierra para indicar el norte y el sur en el globo . Dado que los extremos opuestos de los imanes se atraen, el polo norte de un imán es atraído por el polo sur de otro imán. El polo norte magnético de la Tierra (actualmente en el océano Ártico, al norte de Canadá) es físicamente un polo sur, ya que atrae el polo norte de una brújula. Un campo magnético contiene energía y los sistemas físicos se mueven hacia configuraciones con menor energía. Cuando se coloca material diamagnético en un campo magnético, un dipolo magnético tiende a alinearse en polaridad opuesta a ese campo, lo que reduce la intensidad neta del campo. Cuando se coloca material ferromagnético dentro de un campo magnético, los dipolos magnéticos se alinean con el campo aplicado, expandiendo así las paredes de dominio de los dominios magnéticos.
Monopolos magnéticos
Como un imán de barra obtiene su ferromagnetismo de los electrones distribuidos uniformemente por toda la barra, cuando un imán de barra se corta por la mitad, cada una de las piezas resultantes es un imán de barra más pequeño. Aunque se dice que un imán tiene un polo norte y un polo sur, estos dos polos no pueden separarse entre sí. Un monopolo, si tal cosa existe, sería un tipo nuevo y fundamentalmente diferente de objeto magnético. Actuaría como un polo norte aislado, no unido a un polo sur, o viceversa. Los monopolos llevarían "carga magnética" análoga a la carga eléctrica. A pesar de las búsquedas sistemáticas desde 1931, a partir de 2010 [update], nunca se han observado, y muy bien podrían no existir. [23]
Sin embargo, algunos modelos de física teórica predicen la existencia de estos monopolos magnéticos . Paul Dirac observó en 1931 que, debido a que la electricidad y el magnetismo muestran una cierta simetría , al igual que la teoría cuántica predice que se pueden observar cargas eléctricas individuales positivas o negativas sin la carga opuesta, deberían ser observables polos magnéticos Sur o Norte aislados. Utilizando la teoría cuántica, Dirac demostró que si existen monopolos magnéticos, entonces se podría explicar la cuantización de la carga eléctrica, es decir, por qué las partículas elementales observadas tienen cargas que son múltiplos de la carga del electrón.
Algunas teorías de gran unificación predicen la existencia de monopolos que, a diferencia de las partículas elementales, son solitones (paquetes de energía localizada). Los resultados iniciales del uso de estos modelos para estimar el número de monopolos creados en el Big Bang contradecían las observaciones cosmológicas: los monopolos habrían sido tan abundantes y masivos que habrían detenido hace mucho tiempo la expansión del universo. Sin embargo, la idea de la inflación (para la cual este problema sirvió como motivación parcial) logró resolver este problema, creando modelos en los que los monopolos existían pero eran lo suficientemente raros como para ser consistentes con las observaciones actuales. [24]
Unidades
SI
| Símbolo [25] | Nombre de la cantidad | Nombre de la unidad | Símbolo | Unidades base |
|---|---|---|---|---|
| mi | energía | joule | J = C⋅V = W⋅s | kg⋅m2⋅s − 2 |
| Q | carga eléctrica | culombio | do | A⋅s |
| I | corriente eléctrica | amperio | A = C/s = W/V | A |
| Yo | densidad de corriente eléctrica | amperio por metro cuadrado | A/ m2 | A⋅m −2 |
| U , Δ V ; Δ ϕ ; E , ξ | diferencia de potencial ; voltaje ; fuerza electromotriz | voltio | V = J/C | kg⋅m2⋅s − 3⋅A − 1 |
| R ; Z ; X | resistencia eléctrica ; impedancia ; reactancia | ohm | Ω = V/A | kg⋅m2⋅s − 3⋅A − 2 |
| ρ | resistividad | ohmímetro | Ω⋅m | kg⋅m3⋅s − 3⋅A − 2 |
| PAG | energía eléctrica | vatio | W = V⋅A | kg⋅m2⋅s − 3 |
| do | capacidad | faradio | F = C/V | kg −1 m −2 A 2 s 4 |
| Φ mi | flujo eléctrico | voltímetro | V⋅m | kg⋅m3⋅s − 3⋅A − 1 |
| mi | intensidad del campo eléctrico | voltio por metro | V/m = N/C | kg⋅m⋅A − 1⋅s −3 |
| D | campo de desplazamiento eléctrico | culombio por metro cuadrado | C/ m2 | A⋅s⋅m −2 |
| mi | permitividad | faradio por metro | Mujer/hombre | kg −1 m −3 A 2 s 4 |
| χ y | susceptibilidad eléctrica | ( sin dimensiones ) | 1 | 1 |
| pag | momento dipolar eléctrico | coulombímetro | C⋅m | A⋅s⋅m |
| G ; Y ; B | conductancia ; admitancia ; susceptancia | Siemens | S = Ω −1 | kg −1 ⋅m −2 ⋅s 3 ⋅A 2 |
| κ , γ , σ | conductividad | siemens por metro | Hombre | kg - 1m - 3s3A2 |
| B | densidad de flujo magnético, inducción magnética | tesla | T = Wb/m2 = N⋅A −1 ⋅m −1 | kg⋅s −2 ⋅A −1 |
| Φ , ΦM , ΦB | flujo magnético | Weber | Wb = V⋅s | kg⋅m2⋅s − 2⋅A − 1 |
| yo | Intensidad del campo magnético | amperio por metro | Soy | A⋅m −1 |
| F | fuerza magnetomotriz | amperio | A = Bb/H | A |
| R | reluctancia magnética | henry inverso | H −1 = A/Wb | kg −1 ⋅m −2 ⋅s 2 ⋅A 2 |
| PAG | permeabilidad magnética | Enrique | H = Wb/A | kg⋅m2⋅s - 2⋅A - 2 |
| Yo , yo | inductancia | Enrique | H = Wb/A = V⋅s/A | kg⋅m2⋅s − 2⋅A − 2 |
| micras | permeabilidad | henry por metro | Hombre | kilogramo⋅m⋅s −2 ⋅A −2 |
| χ | susceptibilidad magnética | ( sin dimensiones ) | 1 | 1 |
| metro | momento dipolar magnético | amperio metro cuadrado | A⋅m2 = J⋅T −1 | Soy 2 |
| σ | magnetización de masa | amperio metro cuadrado por kilogramo | A⋅m2 / kg | Un metro cuadrado de masa corporal (kg) -1 |
Otro
- gauss – unidad de campo magnético en centímetros-gramo-segundo (CGS) (denotada B ).
- oersted – la unidad CGS del campo magnetizante (denotado como H )
- Maxwell – la unidad CGS para el flujo magnético
- Gamma: unidad de densidad de flujo magnético que se utilizaba comúnmente antes de que se utilizara el tesla (1,0 gamma = 1,0 nanotesla).
- μ 0 – símbolo común para la permeabilidad del espacio libre ( 4π × 10 −7 newton /( amperio-vuelta ) 2 )
Seres vivos

Algunos organismos pueden detectar campos magnéticos, un fenómeno conocido como magnetocepción . Algunos materiales de los seres vivos son ferromagnéticos, aunque no está claro si las propiedades magnéticas cumplen una función especial o son simplemente un subproducto de contener hierro. Por ejemplo, los quitones , un tipo de molusco marino, producen magnetita para endurecer sus dientes, e incluso los humanos producen magnetita en el tejido corporal. [26]
La magnetobiología estudia los efectos de los campos magnéticos en los organismos vivos; los campos producidos naturalmente por un organismo se conocen como biomagnetismo . Muchos organismos biológicos están compuestos principalmente de agua y, como el agua es diamagnética , los campos magnéticos extremadamente fuertes pueden repeler a estos seres vivos.
Interpretación del magnetismo mediante velocidades relativas
En los años posteriores a 1820, André-Marie Ampère realizó numerosos experimentos en los que midió las fuerzas entre corrientes continuas. En particular, también estudió las fuerzas magnéticas entre cables no paralelos. [27] El resultado final de su trabajo fue una ley de fuerza que ahora lleva su nombre. En 1835, Carl Friedrich Gauss se dio cuenta [12] de que la ley de fuerza de Ampère en su forma original puede explicarse mediante una generalización de la ley de Coulomb .
La ley de fuerza de Gauss establece que la fuerza electromagnética experimentada por una carga puntual, con trayectoria , en la proximidad de otra carga puntual, con trayectoria , en el vacío es igual a la fuerza central
- ,
donde es la distancia entre las cargas y es la velocidad relativa. Wilhelm Eduard Weber confirmó la hipótesis de Gauss en numerosos experimentos. [28] [29] [30] Mediante la electrodinámica de Weber es posible explicar los efectos estáticos y cuasiestáticos en el régimen no relativista de la electrodinámica clásica sin campo magnético ni fuerza de Lorentz .
Desde 1870 se ha desarrollado la electrodinámica de Maxwell , que postula la existencia de campos eléctricos y magnéticos. En la electrodinámica de Maxwell, la fuerza electromagnética real se puede calcular utilizando la fuerza de Lorentz, que, al igual que la fuerza de Weber, depende de la velocidad. Sin embargo, la electrodinámica de Maxwell no es totalmente compatible con el trabajo de Ampère, Gauss y Weber en el régimen cuasiestático. En particular, la ley de fuerza original de Ampère y la ley de Biot-Savart solo son equivalentes si el bucle conductor generador de campo está cerrado. [31] La electrodinámica de Maxwell representa, por tanto, una ruptura con la interpretación del magnetismo de Gauss y Weber, ya que en la electrodinámica de Maxwell ya no es posible deducir la fuerza magnética a partir de una fuerza central.
Origen mecánico-cuántico del magnetismo
Aunque se pueden formular explicaciones heurísticas basadas en la física clásica, el diamagnetismo, el paramagnetismo y el ferromagnetismo solo se pueden explicar completamente utilizando la teoría cuántica. [32] [33] Un modelo exitoso fue desarrollado ya en 1927, por Walter Heitler y Fritz London , quienes derivaron, de manera cuántica-mecánica, cómo se forman las moléculas de hidrógeno a partir de átomos de hidrógeno, es decir, a partir de los orbitales atómicos del hidrógeno y centrados en los núcleos A y B , véase más adelante. Que esto conduzca al magnetismo no es en absoluto obvio, pero se explicará a continuación.
Según la teoría de Heitler-London se forman los llamados orbitales moleculares de dos cuerpos , es decir, el orbital resultante es:
En este caso, el último producto significa que un primer electrón, r 1 , se encuentra en un orbital atómico de hidrógeno centrado en el segundo núcleo, mientras que el segundo electrón gira alrededor del primer núcleo. Este fenómeno de "intercambio" es una expresión de la propiedad mecánico-cuántica de que no se pueden distinguir partículas con propiedades idénticas. Es específico no sólo de la formación de enlaces químicos , sino también del magnetismo. Es decir, en este contexto surge el término interacción de intercambio , un término que es esencial para el origen del magnetismo y que es más fuerte, aproximadamente en factores 100 e incluso 1000, que las energías que surgen de la interacción electrodinámica dipolo-dipolo.
En cuanto a la función de espín , que es responsable del magnetismo, tenemos el principio de Pauli ya mencionado, es decir, que un orbital simétrico (es decir, con el signo + como se indicó anteriormente) debe multiplicarse por una función de espín antisimétrica (es decir, con un signo −), y viceversa . Por lo tanto:
- ,
Es decir, no sólo y deben sustituirse por α y β , respectivamente (la primera entidad significa "spin up", la segunda "spin down"), sino también el signo + por el signo −, y finalmente r i por los valores discretos s i (= ± 1 ⁄ 2 ); por lo tanto tenemos y . El " estado singlete ", es decir, el signo −, significa: los espines son antiparalelos , es decir, para el sólido tenemos antiferromagnetismo , y para moléculas biatómicas tenemos diamagnetismo . La tendencia a formar un enlace químico (homoeopolar) (esto significa: la formación de un orbital molecular simétrico , es decir, con el signo +) resulta a través del principio de Pauli automáticamente en un estado de espín antisimétrico (es decir, con el signo −). Por el contrario, la repulsión coulombiana de los electrones, es decir, la tendencia a que intenten evitarse entre sí mediante esta repulsión, daría lugar a una función orbital antisimétrica (es decir, con el signo −) de estas dos partículas, y complementaria a una función de espín simétrica (es decir, con el signo +, una de las llamadas " funciones triplete "). Por tanto, ahora los espines serían paralelos ( ferromagnetismo en un sólido, paramagnetismo en gases biatómicos).
La última tendencia mencionada predomina en los metales hierro , cobalto y níquel , y en algunas tierras raras, que son ferromagnéticos . La mayoría de los demás metales, en los que predomina la tendencia mencionada en primer lugar, son no magnéticos (por ejemplo , sodio , aluminio y magnesio ) o antiferromagnéticos (por ejemplo, manganeso ). Los gases diatómicos también son casi exclusivamente diamagnéticos y no paramagnéticos. Sin embargo, la molécula de oxígeno, debido a la participación de los orbitales π, es una excepción importante para las ciencias de la vida.
Las consideraciones de Heitler-London pueden generalizarse al modelo de magnetismo de Heisenberg (Heisenberg 1928).
La explicación de los fenómenos se basa así esencialmente en todas las sutilezas de la mecánica cuántica, mientras que la electrodinámica abarca principalmente la fenomenología.
Véase también
- Coercitividad
- Gravitomagnetismo
- Histéresis magnética
- Magneto
- Cojinete magnético
- Circuito magnético
- Refrigeración magnética
- Película de visualización del campo magnético
- Agitador magnético
- Fuente de alimentación conmutada
- Estructura magnética
- Micromagnetismo
- Imán de neodimio
- Imán de plástico
- Imán de tierras raras
- Onda de giro
- Magnetización espontánea
- Magnetómetro de muestra vibratoria
- Libros de texto sobre electromagnetismo
Referencias
- ^ Jiles, David (2 de septiembre de 2015). Introducción al magnetismo y los materiales magnéticos (tercera edición). Boca Raton. ISBN 978-1-4822-3887-7.OCLC 909323904 .
{{cite book}}: CS1 maint: location missing publisher (link) - ^ Du, Yaping; Cheng, TC; Farag, AS (agosto de 1996). "Principios de protección del campo magnético de frecuencia industrial con láminas planas en una fuente de conductores largos". IEEE Transactions on Electromagnetic Compatibility . 38 (3): 450–459. doi :10.1109/15.536075. ISSN 1558-187X.
- ^ Du Trémolet de Lacheisserie, Étienne; Damián Gignoux; Michel Schlenker (2005). Magnetismo: Fundamentos. Saltador. págs. 3–6. ISBN 978-0-387-22967-6.
- ^ Ópera Platonis, Meyer y Zeller, 1839, pág. 989.
- ^ La ubicación de Magnesia es motivo de debate; podría ser la región de Grecia continental o Magnesia ad Sipylum . Véase, por ejemplo, "Magnet". Blog de Language Hat . 28 de mayo de 2005. Consultado el 22 de marzo de 2013 .
- ^ Fowler, Michael (1997). "Comienzos históricos de las teorías de la electricidad y el magnetismo" . Consultado el 2 de abril de 2008 .
- ^ Kumar Goyal, Rajendra (2017). Nanomateriales y nanocompuestos: síntesis, propiedades, técnicas de caracterización y aplicaciones . CRC Press. pág. 171. ISBN 9781498761673.
- ^ La sección "Fanying 2" (反應第二) de El Guiguzi : "其察言也,不失若磁石之取鍼,舌之取燔骨".
- ^ Li, Shu-hua (1954). "Origine de la Boussole II. Aimant et Boussole". Isis (en francés). 45 (2): 175-196. doi :10.1086/348315. JSTOR 227361. S2CID 143585290.
un pasaje dans le
Liu-che-tch'ouen-ts'ieou
[...]: "La pierre d'aimant fait venir le fer ou elle l'attire".
De la sección " Jingtong " (精通) del "Almanaque del último mes de otoño" (季秋紀): "慈石召鐵,或引之也]" - ↑ En la sección "Una última palabra sobre los dragones" (亂龍篇 Luanlong ) del Lunheng : " El ámbar toma pajitas y una piedra de carga atrae agujas" (頓牟掇芥,磁石引針).
- ^ Schmidl, Petra G. (1996–1997). "Dos fuentes árabes tempranas sobre la brújula magnética". Revista de estudios árabes e islámicos . 1 : 81–132.
- ^ ab Gauss, Carl Friedrich (1867). Carl Friedrich Gauss Werke. Banda Fünfter . Königliche Gesellschaft der Wissenschaften zu Göttingen. pag. 617.
- ^ ab A. Einstein: "Sobre la electrodinámica de los cuerpos en movimiento", 30 de junio de 1905.
- ^ HP Meyers (1997). Introducción a la física del estado sólido (2.ª ed.). CRC Press. pág. 362; Figura 11.1. ISBN 9781420075021.
- ^ Catherine Westbrook; Carolyn Kaut; Carolyn Kaut-Roth (1998). Resonancia magnética en la práctica (2.ª ed.). Wiley-Blackwell. pág. 217. ISBN 978-0-632-04205-0.
- ^ Greshko, Michael (20 de enero de 2024). «Los científicos acaban de descubrir un nuevo tipo de magnetismo». Wired . ISSN 1059-1028 . Consultado el 8 de febrero de 2024 .
- ^ Purcell 2012, pág. 320.584
- ^ Merzouki, Rochdi; Samantaray, Arun Kumar; Pathak, Pushparaj Mani (2012). Sistemas mecatrónicos inteligentes: modelado, control y diagnóstico. Springer Science & Business Media. págs. 403–405. ISBN 978-1447146285.
- ^ Sturgeon, W. (1825). "Aparato electromagnético mejorado". Trad. Royal Society of Arts, Manufactures, & Commerce . 43 : 37–52.citado en Miller, TJE (2001). Control electrónico de máquinas de reluctancia conmutada. Newnes. pág. 7. ISBN 978-0-7506-5073-1.
- ^ Griffiths 1998, capítulo 12
- ^ Boozer, Allen H. (1 de abril de 2006). "Perturbación de la intensidad del campo magnético". Física de plasmas . 13 (4): 044501. Bibcode :2006PhPl...13d4501B. doi :10.1063/1.2192511. ISSN 1070-664X.
- ^ Jackson, John David (1999). Electrodinámica clásica (3.ª ed.). Nueva York: Wiley . ISBN 978-0-471-30932-1.
- ^ Milton menciona algunos eventos no concluyentes (p. 60) y aun así concluye que "no ha sobrevivido ninguna evidencia de monopolos magnéticos" (p. 3). Milton, Kimball A. (junio de 2006). "Estado teórico y experimental de los monopolos magnéticos". Informes sobre el progreso en física . 69 (6): 1637–1711. arXiv : hep-ex/0602040 . Bibcode :2006RPPh...69.1637M. doi :10.1088/0034-4885/69/6/R02. S2CID 119061150..
- ^ Guth, Alan (1997). El universo inflacionario: la búsqueda de una nueva teoría de los orígenes cósmicos . Perseo. ISBN 978-0-201-32840-0.OCLC 38941224 ..
- ^ Unión Internacional de Química Pura y Aplicada (1993). Cantidades, unidades y símbolos en química física , 2.ª edición, Oxford: Blackwell Science. ISBN 0-632-03583-8 . pp. 14-15. Versión electrónica.
- ^ Kirschvink, Joseph L.; Kobayashi-Kirshvink, Atsuko; Diaz-Ricci, Juan C.; Kirschvink, Steven J. (1992). "Magnetita en tejidos humanos: un mecanismo para los efectos biológicos de campos magnéticos ELF débiles" (PDF) . Suplemento de bioelectromagnetismo . 1 : 101–113. doi :10.1002/bem.2250130710. PMID 1285705 . Consultado el 29 de marzo de 2016 .
- ^ Assis, AKT; JPMC Chaib (2015). Electrodinámica de Ampère: Análisis del significado y evolución de la fuerza de Ampère entre elementos actuales, junto con una traducción completa de su obra maestra: Teoría de los fenómenos electrodinámicos, deducida únicamente de la experiencia . C. Roy Keys Inc. ISBN 978-1-987980-03-5.
- ^ Wilhelm Weber (2021). Andre Koch Torres Assis (ed.). Principales obras de Wilhelm Weber en electrodinámica traducidas al inglés. Volumen I: Sistema absoluto de unidades de Gauss y Weber . Apeiron Montreal.
- ^ Wilhelm Weber (2021). Andre Koch Torres Assis (ed.). Principales obras de Wilhelm Weber en electrodinámica traducidas al inglés. Volumen II: La fuerza fundamental de Weber y la unificación de las leyes de Coulomb, Ampere y Faraday . Apeiron Montreal.
- ^ Wilhelm Weber (2021). Andre Koch Torres Assis (ed.). Principales obras de Wilhelm Weber en electrodinámica traducidas al inglés. Volumen III: Medición de la constante c de Weber, diamagnetismo, la ecuación telegráfica y la propagación de ondas eléctricas a la velocidad de la luz . Apeiron Montreal.
- ^ Maxwell, James Clerk (1881). Tratado sobre electricidad y magnetismo. Volumen 2. Vol. 2 (2.ª ed.). The Clarendon Press, Oxdord. pág. 162.
- ^ "Las Conferencias Feynman sobre Física, vol. II, cap. 34: El magnetismo de la materia". www.feynmanlectures.caltech.edu .
- ^ "Las Conferencias Feynman sobre Física, vol. II, cap. 36: Ferromagnetismo". www.feynmanlectures.caltech.edu .
Lectura adicional
- David K. Cheng (1992). Electromagnetismo de campo y de onda . Addison-Wesley Publishing Company, Inc. ISBN 978-0-201-12819-2.
- Furlani, Edward P. (2001). Imanes permanentes y dispositivos electromecánicos: materiales, análisis y aplicaciones . Academic Press . ISBN 978-0-12-269951-1.OCLC 162129430 .
- Griffiths, David J. (1998). Introducción a la electrodinámica (3.ª ed.) . Prentice Hall. ISBN 978-0-13-805326-0.OCLC 40251748 .
- Kronmüller, Helmut. (2007). Manual de magnetismo y materiales magnéticos avanzados, 5 volúmenes . John Wiley & Sons. ISBN 978-0-470-02217-7.OCLC 124165851 .
- Purcell, Edward M. (2012). Electricidad y magnetismo (3.ª ed.). Cambridge: Cambridge Univ. Press. ISBN 9781-10701-4022.
- Tipler, Paul (2004). Física para científicos e ingenieros: electricidad, magnetismo, luz y física moderna elemental (5.ª ed.) . WH Freeman. ISBN 978-0-7167-0810-0.OCLC 51095685 .
- Coey, JMD (2019). Magnetismo y materiales magnéticos . Cambridge University Press. ISBN 978-1108717519.
Bibliografía
- Snacks científicos del Exploratorium – Tema: Física/Electricidad y magnetismo
- Una colección de estructuras magnéticas – MAGNDATA































