Histéresis
Dependencia del estado de un sistema con respecto a su historia
Campo de desplazamiento eléctrico D de un material ferroeléctrico a medida que el campo eléctrico E primero disminuye y luego aumenta. Las curvas forman un bucle de histéresis .

La histéresis es la dependencia del estado de un sistema con respecto a su historia. Por ejemplo, un imán puede tener más de un momento magnético posible en un campo magnético dado , dependiendo de cómo haya cambiado el campo en el pasado. Los gráficos de un solo componente del momento a menudo forman un bucle o curva de histéresis, donde hay diferentes valores de una variable dependiendo de la dirección de cambio de otra variable. Esta dependencia de la historia es la base de la memoria en una unidad de disco duro y la remanencia que conserva un registro de la magnitud del campo magnético de la Tierra en el pasado. La histéresis ocurre en materiales ferromagnéticos y ferroeléctricos , así como en la deformación de bandas de goma y aleaciones con memoria de forma y muchos otros fenómenos naturales. En los sistemas naturales, a menudo se asocia con cambios termodinámicos irreversibles, como transiciones de fase y con fricción interna ; y la disipación es un efecto secundario común.

La histéresis se puede encontrar en física , química , ingeniería , biología y economía . Se incorpora en muchos sistemas artificiales: por ejemplo, en termostatos y disparadores Schmitt , evita cambios frecuentes no deseados.

La histéresis puede ser un desfase dinámico entre una entrada y una salida que desaparece si la entrada varía más lentamente; esto se conoce como histéresis dependiente de la velocidad . Sin embargo, fenómenos como los bucles de histéresis magnética son principalmente independientes de la velocidad , lo que hace posible una memoria duradera.

Los sistemas con histéresis son no lineales y su modelado puede resultar complicado desde el punto de vista matemático. Algunos modelos histeréticos, como el modelo de Preisach (originalmente aplicado al ferromagnetismo) y el modelo de Bouc-Wen , intentan captar características generales de la histéresis; también existen modelos fenomenológicos para fenómenos particulares, como el modelo de Jiles-Atherton para el ferromagnetismo.

Resulta difícil definir la histéresis con precisión. Isaak D. Mayergoyz escribió: "... el significado mismo de la histéresis varía de un área a otra, de un artículo a otro y de un autor a otro. Como resultado, se necesita una definición matemática estricta de la histéresis para evitar confusiones y ambigüedades". [1]

Etimología e historia

El término "histéresis" se deriva de ὑστέρησις , una palabra griega antigua que significa "deficiencia" o "rezago". Fue acuñado en 1881 por Sir James Alfred Ewing para describir el comportamiento de los materiales magnéticos. [2]

Algunos de los primeros trabajos sobre la descripción de la histéresis en sistemas mecánicos fueron realizados por James Clerk Maxwell . Posteriormente, los modelos histeréticos recibieron una atención significativa en los trabajos de Ferenc Preisach ( modelo de histéresis de Preisach ), Louis Néel y Douglas Hugh Everett en relación con el magnetismo y la absorción. Una teoría matemática más formal de los sistemas con histéresis fue desarrollada en la década de 1970 por un grupo de matemáticos rusos dirigido por Mark Krasnosel'skii .

Tipos

Dependiente de la tasa

Un tipo de histéresis es un desfase entre la entrada y la salida. Un ejemplo es una entrada sinusoidal X(t) que da como resultado una salida sinusoidal Y(t) , pero con un desfase de fase φ :

incógnita ( a ) = incógnita 0 pecado ⁡ ω a Y ( a ) = Y 0 pecado ⁡ ( ω a − φ ) . {\displaystyle {\begin{aligned}X(t)&=X_{0}\sin \omega t\\Y(t)&=Y_{0}\sin \left(\omega t-\varphi \right).\end{aligned}}}

Tal comportamiento puede ocurrir en sistemas lineales y una forma más general de respuesta es

Y ( a ) = χ i incógnita ( a ) + ∫ 0 ∞ Φ d ( τ ) incógnita ( a − τ ) d τ , {\displaystyle Y(t)=\chi _{\text{i}}X(t)+\int _{0}^{\infty }\Phi _{\text{d}}(\tau )X( t-\tau )\,\mathrm {d} \tau ,}

donde es la respuesta instantánea y es la respuesta al impulso a un impulso que ocurrió hace unidades de tiempo. En el dominio de frecuencia , la entrada y la salida están relacionadas por una susceptibilidad generalizada compleja que se puede calcular a partir de ; es matemáticamente equivalente a una función de transferencia en la teoría de filtros lineales y el procesamiento de señales analógicas. [3] χ i {\displaystyle \chi _{\text{i}}} Φ d ( τ ) {\displaystyle \Phi _ {d}(\tau )} τ {\estilo de visualización \tau} Φ d {\displaystyle \Phi_{d}}

Este tipo de histéresis se conoce a menudo como histéresis dependiente de la velocidad . Si la entrada se reduce a cero, la salida continúa respondiendo durante un tiempo finito. Esto constituye un recuerdo del pasado, pero limitado porque desaparece cuando la salida decae a cero. El desfase depende de la frecuencia de la entrada y se vuelve cero a medida que la frecuencia disminuye. [3]

Cuando la histéresis dependiente de la velocidad se debe a efectos disipativos como la fricción , se asocia con pérdida de potencia. [3]

Independiente de la tasa

Los sistemas con histéresis independiente de la velocidad tienen una memoria persistente del pasado que permanece después de que los transitorios se han extinguido. [4] El desarrollo futuro de un sistema de este tipo depende de la historia de los estados visitados, pero no se desvanece a medida que los eventos retroceden al pasado. Si una variable de entrada X(t) pasa de X 0 a X 1 y viceversa, la salida Y(t) puede ser Y 0 inicialmente, pero un valor diferente Y 2 al regresar. Los valores de Y(t) dependen de la ruta de valores que X(t) recorre, pero no de la velocidad a la que recorre la ruta. [3] Muchos autores restringen el término histéresis para que signifique solo histéresis independiente de la velocidad. [5] Los efectos de histéresis se pueden caracterizar utilizando el modelo de Preisach y el modelo generalizado de Prandtl−Ishlinskii. [6]

En ingeniería

Sistemas de control

En los sistemas de control, la histéresis se puede utilizar para filtrar señales de modo que la salida reaccione con menor rapidez de lo que lo haría de otro modo, teniendo en cuenta el historial reciente del sistema. Por ejemplo, un termostato que controla un calentador puede encenderlo cuando la temperatura cae por debajo de A, pero no apagarlo hasta que la temperatura sube por encima de B. (Por ejemplo, si se desea mantener una temperatura de 20 °C, se puede configurar el termostato para que encienda el calentador cuando la temperatura caiga por debajo de 18 °C y lo apague cuando la temperatura supere los 22 °C).

De manera similar, se puede diseñar un interruptor de presión para que muestre histéresis, con puntos de ajuste de presión sustituidos por umbrales de temperatura.

Circuitos electrónicos

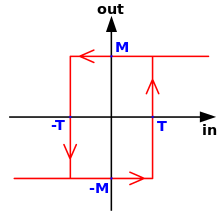
Bucle de histéresis agudo de un disparador Schmitt

A menudo, se añade intencionalmente cierta cantidad de histéresis a un circuito electrónico para evitar cambios rápidos no deseados. Esta y otras técnicas similares se utilizan para compensar el rebote de contacto en los interruptores o el ruido en una señal eléctrica.

Un disparador Schmitt es un circuito electrónico simple que exhibe esta propiedad.

Un relé de enclavamiento utiliza un solenoide para activar un mecanismo de trinquete que mantiene el relé cerrado incluso si se interrumpe la alimentación del relé.

Una cierta retroalimentación positiva desde la salida a una entrada de un comparador puede aumentar la histéresis natural (una función de su ganancia) que exhibe.

La histéresis es esencial para el funcionamiento de algunos memristores (componentes del circuito que "recuerdan" los cambios en la corriente que pasa a través de ellos al cambiar su resistencia). [7]

La histéresis se puede utilizar al conectar conjuntos de elementos como nanoelectrónica , celdas electrocromáticas y dispositivos con efecto memoria mediante direccionamiento matricial pasivo . Se crean atajos entre componentes adyacentes (ver diafonía ) y la histéresis ayuda a mantener los componentes en un estado particular mientras los otros componentes cambian de estado. De esta manera, se pueden direccionar todas las filas al mismo tiempo en lugar de hacerlo individualmente.

En el campo de la electrónica de audio, una puerta de ruido a menudo implementa histéresis intencionalmente para evitar que la puerta "vibre" cuando se aplican señales cercanas a su umbral.

Diseño de interfaz de usuario

A veces se añade una histéresis de forma intencionada a los algoritmos informáticos . El campo del diseño de interfaces de usuario ha tomado prestado el término histéresis para referirse a los momentos en los que el estado de la interfaz de usuario se retrasa intencionadamente con respecto a la entrada aparente del usuario. Por ejemplo, un menú que se dibujó en respuesta a un evento de desplazamiento del ratón puede permanecer en la pantalla durante un breve instante después de que el ratón se haya movido fuera de la región de activación y de la región del menú. Esto permite al usuario mover el ratón directamente a un elemento del menú, incluso si parte de esa ruta directa del ratón está fuera de la región de activación y de la región del menú. Por ejemplo, al hacer clic con el botón derecho en el escritorio en la mayoría de las interfaces de Windows se creará un menú que exhibe este comportamiento.

Aerodinámica

En aerodinámica , la histéresis se puede observar cuando disminuye el ángulo de ataque de un ala después de una pérdida, en relación con los coeficientes de sustentación y resistencia. El ángulo de ataque en el que el flujo en la parte superior del ala se reincorpora es generalmente menor que el ángulo de ataque en el que el flujo se separa durante el aumento del ángulo de ataque. [8]

Hidráulica

La histéresis se puede observar en la relación de caudal-nivel de un río durante condiciones que cambian rápidamente, como el paso de una ola de inundación. Es más pronunciada en corrientes de bajo gradiente con hidrogramas de borde de ataque pronunciados. [9]

Reacción

Las piezas móviles de las máquinas, como los componentes de un tren de engranajes , normalmente tienen un pequeño espacio entre ellas para permitir el movimiento y la lubricación. Como consecuencia de este espacio, cualquier inversión de dirección de una pieza motriz no se transmitirá inmediatamente a la pieza accionada. [10] Este retraso no deseado normalmente se mantiene lo más pequeño posible y suele denominarse juego . La cantidad de juego aumentará con el tiempo a medida que se desgasten las superficies de las piezas móviles.

En mecanica

Histéresis elástica

Histéresis elástica de una banda de goma idealizada. El área en el centro del bucle de histéresis es la energía disipada debido a la fricción interna.

En la histéresis elástica del caucho, el área en el centro de un bucle de histéresis es la energía disipada debido a la fricción interna del material .

La histéresis elástica fue uno de los primeros tipos de histéresis que se examinaron. [11] [12]

El efecto se puede demostrar utilizando una banda elástica con pesas adheridas a ella. Si la parte superior de una banda elástica se cuelga de un gancho y se adhieren pequeñas pesas a la parte inferior de la banda una a la vez, se estirará y se hará más larga. A medida que se cargan más pesas sobre ella, la banda continuará estirándose porque la fuerza que ejercen las pesas sobre la banda aumenta. Cuando se quita cada peso, o se descarga , la banda se contrae a medida que se reduce la fuerza. A medida que se quitan las pesas, cada peso que produjo una longitud específica cuando se cargó en la banda ahora se contrae menos, lo que resulta en una longitud ligeramente mayor cuando se descarga. Esto se debe a que la banda no obedece perfectamente la ley de Hooke . El ciclo de histéresis de una banda elástica idealizada se muestra en la figura.

En términos de fuerza, la banda elástica era más difícil de estirar cuando estaba cargada que cuando estaba descargada. En términos de tiempo, cuando la banda está descargada, el efecto (la longitud) quedó rezagado con respecto a la causa (la fuerza de las pesas) porque la longitud aún no había alcanzado el valor que tenía para el mismo peso durante la parte de carga del ciclo. En términos de energía, se requirió más energía durante la carga que durante la descarga, y el exceso de energía se disipó en forma de energía térmica.

La histéresis elástica es más pronunciada cuando la carga y descarga se realiza rápidamente que cuando se realiza lentamente. [13] Algunos materiales, como los metales duros, no muestran histéresis elástica bajo una carga moderada, mientras que otros materiales duros, como el granito y el mármol, sí la presentan. Los materiales como el caucho presentan un alto grado de histéresis elástica.

Cuando se mide la histéresis intrínseca del caucho, se puede considerar que el material se comporta como un gas. Cuando se estira una banda de caucho, se calienta y, si se la suelta de repente, se enfría perceptiblemente. Estos efectos corresponden a una gran histéresis debida al intercambio térmico con el entorno y a una histéresis menor debida a la fricción interna en el caucho. Esta histéresis propiamente dicha, intrínseca, solo se puede medir si la banda de caucho está aislada térmicamente .

Las suspensiones de vehículos pequeños que utilizan caucho (u otros elastómeros ) pueden lograr la doble función de amortiguación y elasticidad, ya que el caucho, a diferencia de los resortes de metal, tiene una histéresis pronunciada y no devuelve toda la energía de compresión absorbida en el rebote. Las bicicletas de montaña han hecho uso de suspensiones de elastómero, al igual que el automóvil Mini original.

La causa principal de la resistencia a la rodadura cuando un cuerpo (como una pelota, un neumático o una rueda) rueda sobre una superficie es la histéresis. Esto se atribuye a las características viscoelásticas del material del cuerpo rodante.

Histéresis del ángulo de contacto

El ángulo de contacto formado entre una fase líquida y una sólida exhibirá un rango de ángulos de contacto que son posibles. Hay dos métodos comunes para medir este rango de ángulos de contacto. El primer método se conoce como el método de base inclinada. Una vez que se dispensa una gota sobre la superficie con el nivel de la superficie, la superficie se inclina de 0° a 90°. A medida que se inclina la gota, el lado de la pendiente descendente estará en un estado de humectación inminente mientras que el lado de la pendiente ascendente estará en un estado de deshumectación inminente. A medida que aumenta la inclinación, el ángulo de contacto de la pendiente descendente aumentará y representará el ángulo de contacto de avance mientras que el lado de la pendiente ascendente disminuirá; este es el ángulo de contacto de retroceso. Los valores de estos ángulos justo antes de la liberación de la gota generalmente representarán los ángulos de contacto de avance y retroceso. La diferencia entre estos dos ángulos es la histéresis del ángulo de contacto.

El segundo método se conoce a menudo como el método de adición/eliminación de volumen. Cuando se elimina el volumen máximo de líquido de la gota sin que disminuya el área interfacial, se mide el ángulo de contacto de retroceso. Cuando se agrega volumen al máximo antes de que aumente el área interfacial, este es el ángulo de contacto de avance . Al igual que con el método de inclinación, la diferencia entre los ángulos de contacto de avance y retroceso es la histéresis del ángulo de contacto. La mayoría de los investigadores prefieren el método de inclinación; el método de adición/eliminación requiere que una punta o aguja permanezca incrustada en la gota, lo que puede afectar la precisión de los valores, especialmente el ángulo de contacto de retroceso.

Histéresis de la forma de la burbuja

Las formas de equilibrio de las burbujas que se expanden y contraen en capilares ( agujas romas ) pueden exhibir histéresis dependiendo de la magnitud relativa de la presión capilar máxima a la presión ambiental, y la magnitud relativa del volumen de la burbuja a la presión capilar máxima al volumen muerto en el sistema. [14] La histéresis de la forma de la burbuja es una consecuencia de la compresibilidad del gas , que hace que las burbujas se comporten de manera diferente durante la expansión y la contracción. Durante la expansión, las burbujas experimentan grandes saltos de no equilibrio en el volumen, mientras que durante la contracción las burbujas son más estables y experimentan un salto relativamente más pequeño en el volumen que resulta en una asimetría durante la expansión y la contracción. La histéresis de la forma de la burbuja es cualitativamente similar a la histéresis de adsorción, y como en la histéresis del ángulo de contacto, las propiedades interfaciales juegan un papel importante en la histéresis de la forma de la burbuja.

La existencia de la histéresis de la forma de la burbuja tiene consecuencias importantes en los experimentos de reología interfacial que involucran burbujas. Como resultado de la histéresis, no todos los tamaños de burbujas pueden formarse en un capilar. Además, la compresibilidad del gas que causa la histéresis conduce a complicaciones no deseadas en la relación de fase entre los cambios aplicados en el área interfacial y las tensiones interfaciales esperadas. Estas dificultades se pueden evitar diseñando sistemas experimentales que eviten la histéresis de la forma de la burbuja. [14] [15]

Histéresis de adsorción

La histéresis también puede producirse durante los procesos de adsorción física . En este tipo de histéresis, la cantidad adsorbida es diferente cuando se añade gas que cuando se lo retira. Las causas específicas de la histéresis de adsorción siguen siendo un área de investigación activa, pero están vinculadas a diferencias en los mecanismos de nucleación y evaporación dentro de los mesoporos. Estos mecanismos se complican aún más por efectos como la cavitación y el bloqueo de los poros.

En la adsorción física, la histéresis es evidencia de mesoporosidad ; de hecho, la definición de mesoporos (2–50 nm) está asociada con la aparición (50 nm) y desaparición (2 nm) de la mesoporosidad en las isotermas de adsorción de nitrógeno como una función del radio Kelvin. [16] Una isoterma de adsorción que muestra histéresis se dice que es de Tipo IV (para un adsorbato humectante) o Tipo V (para un adsorbato no humectante), y los bucles de histéresis en sí mismos se clasifican de acuerdo con qué tan simétrico es el bucle. [17] Los bucles de histéresis de adsorción también tienen la propiedad inusual de que es posible escanear dentro de un bucle de histéresis invirtiendo la dirección de adsorción mientras se está en un punto del bucle. Los escaneos resultantes se denominan "cruzamiento", "convergencia" o "retorno", según la forma de la isoterma en este punto. [18]

Histéresis del potencial mátrico

La relación entre el potencial hídrico mátrico y el contenido de agua es la base de la curva de retención de agua . Las mediciones del potencial mátrico (Ψ m ) se convierten en mediciones de contenido volumétrico de agua (θ) según una curva de calibración específica del sitio o del suelo. La histéresis es una fuente de error en la medición del contenido de agua. La histéresis del potencial mátrico surge de las diferencias en el comportamiento de humectación que hacen que el medio seco se vuelva a humedecer; es decir, depende del historial de saturación del medio poroso. El comportamiento histéresis significa que, por ejemplo, a un potencial mátrico (Ψ m ) de 5 kPa , el contenido volumétrico de agua (θ) de una matriz de suelo arenoso fino podría ser cualquier valor entre el 8% y el 25%. [19]

Los tensiómetros se ven directamente influenciados por este tipo de histéresis. Otros dos tipos de sensores utilizados para medir el potencial mátrico del agua del suelo también se ven influenciados por los efectos de histéresis dentro del propio sensor. Los bloques de resistencia, tanto de nailon como de yeso, miden el potencial mátrico en función de la resistencia eléctrica. La relación entre la resistencia eléctrica del sensor y el potencial mátrico del sensor es histéresis. Los termopares miden el potencial mátrico en función de la disipación de calor. La histéresis se produce porque la disipación de calor medida depende del contenido de agua del sensor, y la relación entre el contenido de agua del sensor y el potencial mátrico es histéresis. A partir de 2002 [actualizar], solo se miden las curvas de desorción durante la calibración de los sensores de humedad del suelo . A pesar de que puede ser una fuente de error significativo, el efecto específico del sensor de la histéresis generalmente se ignora. [20]

En materiales

Histéresis magnética

Modelo teórico de la magnetización m frente al campo magnético h . Partiendo del origen, la curva ascendente es la curva de magnetización inicial . La curva descendente después de la saturación, junto con la curva de retorno inferior, forman el bucle principal . Los puntos de corte h c y m rs son la coercitividad y la remanencia de saturación .

Cuando se aplica un campo magnético externo a un material ferromagnético como el hierro , los dominios atómicos se alinean con él. Incluso cuando se elimina el campo, se conservará parte de la alineación: el material se ha magnetizado . Una vez magnetizado, el imán permanecerá magnetizado indefinidamente. Para desmagnetizarlo se requiere calor o un campo magnético en sentido contrario. Este es el efecto que proporciona el elemento de memoria en una unidad de disco duro .

La relación entre la intensidad de campo H y la magnetización M no es lineal en tales materiales. Si se desmagnetiza un imán ( H = M = 0 ) y se traza la relación entre H y M para niveles crecientes de intensidad de campo, M sigue la curva de magnetización inicial . Esta curva aumenta rápidamente al principio y luego se acerca a una asíntota llamada saturación magnética . Si ahora el campo magnético se reduce monótonamente, M sigue una curva diferente. Con una intensidad de campo cero, la magnetización se desplaza con respecto al origen en una cantidad llamada remanencia . Si se traza la relación HM para todas las intensidades del campo magnético aplicado, el resultado es un bucle de histéresis llamado bucle principal . El ancho de la sección media es el doble de la coercitividad del material. [21]

Una mirada más de cerca a una curva de magnetización generalmente revela una serie de pequeños saltos aleatorios en la magnetización llamados saltos de Barkhausen . Este efecto se debe a defectos cristalográficos como las dislocaciones . [22]

Los bucles de histéresis magnética no son exclusivos de los materiales con ordenamiento ferromagnético. Otros ordenamientos magnéticos, como el ordenamiento del vidrio de espín , también presentan este fenómeno. [23]

Origen físico

El fenómeno de la histéresis en los materiales ferromagnéticos es el resultado de dos efectos: la rotación de la magnetización y los cambios en el tamaño o número de los dominios magnéticos . En general, la magnetización varía (en dirección pero no en magnitud) a lo largo de un imán, pero en imanes suficientemente pequeños, no lo hace. En estos imanes de dominio único , la magnetización responde a un campo magnético girando. Los imanes de dominio único se utilizan siempre que se necesita una magnetización fuerte y estable (por ejemplo, grabación magnética ).

Los imanes más grandes se dividen en regiones llamadas dominios . En cada dominio, la magnetización no varía; pero entre los dominios hay paredes de dominio relativamente delgadas en las que la dirección de magnetización rota de la dirección de un dominio a otro. Si el campo magnético cambia, las paredes se mueven, cambiando los tamaños relativos de los dominios. Debido a que los dominios no están magnetizados en la misma dirección, el momento magnético por unidad de volumen es menor de lo que sería en un imán de un solo dominio; pero las paredes de dominio implican la rotación de solo una pequeña parte de la magnetización, por lo que es mucho más fácil cambiar el momento magnético. La magnetización también puede cambiar por adición o sustracción de dominios (llamado nucleación y desnucleación ).

Modelos de histéresis magnética

Los modelos empíricos más conocidos en histéresis son los modelos de Preisach y Jiles-Atherton . Estos modelos permiten un modelado preciso del ciclo de histéresis y son ampliamente utilizados en la industria. Sin embargo, estos modelos pierden la conexión con la termodinámica y no se asegura la consistencia energética. Un modelo más reciente, con una base termodinámica más consistente, es el modelo de histéresis consistente no conservativa incremental vectorial (VINCH) de Lavet et al. (2011) [24].

Aplicaciones

Existe una gran variedad de aplicaciones de la histéresis en los ferroimanes. Muchos de ellos hacen uso de su capacidad para retener una memoria, por ejemplo, cintas magnéticas , discos duros y tarjetas de crédito . En estas aplicaciones, son deseables los imanes duros (alta coercitividad) como el hierro , de modo que se absorba la mayor cantidad de energía posible durante la operación de escritura y la información magnetizada resultante no se borre fácilmente.

Por otro lado, el hierro magnéticamente blando (de baja coercitividad) se utiliza para los núcleos de los electroimanes . La baja coercitividad minimiza la pérdida de energía asociada con la histéresis, ya que el campo magnético se invierte periódicamente en presencia de una corriente alterna. La baja pérdida de energía durante un bucle de histéresis es la razón por la que se utiliza hierro dulce para los núcleos de los transformadores y los motores eléctricos.

Histéresis eléctrica

La histéresis eléctrica se produce normalmente en materiales ferroeléctricos , donde los dominios de polarización contribuyen a la polarización total. La polarización es el momento dipolar eléctrico (ya sea C · m −2 o C · m ). El mecanismo, una organización de la polarización en dominios, es similar al de la histéresis magnética.

Transiciones de fase líquida a sólida

La histéresis se manifiesta en transiciones de estado cuando la temperatura de fusión y la temperatura de congelación no coinciden. Por ejemplo, el agar se funde a 85 °C (185 °F) y se solidifica de 32 a 40 °C (90 a 104 °F). Es decir, una vez que el agar se funde a 85 °C, conserva un estado líquido hasta que se enfría a 40 °C. Por lo tanto, desde las temperaturas de 40 a 85 °C, el agar puede ser sólido o líquido, dependiendo del estado en el que se encontraba antes.

En biología

Biología celular y genética

La histéresis en biología celular suele seguir a los sistemas biestables en los que el mismo estado de entrada puede dar lugar a dos salidas diferentes y estables. En los casos en los que la biestabilidad puede dar lugar a salidas digitales, similares a interruptores, a partir de las entradas continuas de concentraciones y actividades químicas, la histéresis hace que estos sistemas sean más resistentes al ruido. Estos sistemas suelen caracterizarse por valores más altos de la entrada necesaria para cambiar a un estado particular en comparación con la entrada necesaria para permanecer en el estado, lo que permite una transición que no es continuamente reversible y, por lo tanto, menos susceptible al ruido.

Las células que experimentan división celular presentan histéresis, ya que se necesita una mayor concentración de ciclinas para pasar de la fase G2 a la mitosis que para permanecer en la mitosis una vez comenzada. [25] [26]

Los sistemas bioquímicos también pueden mostrar resultados similares a la histéresis cuando se trata de estados que varían lentamente y que no se controlan directamente, como en el caso de la detención del ciclo celular en levaduras expuestas a la feromona de apareamiento. [27] Aquí, la duración de la detención del ciclo celular depende no solo del nivel final de entrada Fus3, sino también de los niveles de Fus3 alcanzados previamente. Este efecto se logra debido a las escalas de tiempo más lentas involucradas en la transcripción del intermediario Far1, de modo que la actividad total de Far1 alcanza su valor de equilibrio lentamente, y para cambios transitorios en la concentración de Fus3, la respuesta del sistema depende de la concentración de Far1 alcanzada con el valor transitorio. Los experimentos en este tipo de histéresis se benefician de la capacidad de cambiar la concentración de las entradas con el tiempo. Los mecanismos a menudo se dilucidan permitiendo el control independiente de la concentración del intermediario clave, por ejemplo, mediante el uso de un promotor inducible.

Darlington en sus obras clásicas sobre genética [28] [29] discutió la histéresis de los cromosomas , con lo que quería decir "el fracaso de la forma externa de los cromosomas para responder inmediatamente a las tensiones internas debido a los cambios en su espiral molecular", ya que se encuentran en un medio algo rígido en el espacio limitado del núcleo celular .

En biología del desarrollo , la diversidad de tipos celulares está regulada por moléculas de señalización de acción a largo plazo llamadas morfógenos que modelan grupos uniformes de células de una manera dependiente de la concentración y el tiempo. El morfógeno sonic hedgehog (Shh), por ejemplo, actúa sobre los esbozos de las extremidades y los progenitores neuronales para inducir la expresión de un conjunto de factores de transcripción que contienen homeodominio para subdividir estos tejidos en dominios distintos. Se ha demostrado que estos tejidos tienen una "memoria" de exposición previa a Shh. [30] En el tejido neuronal, esta histéresis está regulada por un circuito de retroalimentación de homeodominio (HD) que amplifica la señalización de Shh. [31] En este circuito, se suprime la expresión de los factores de transcripción Gli , los ejecutores de la vía Shh. Las Glis se procesan en formas represoras (GliR) en ausencia de Shh, pero en presencia de Shh, una proporción de Glis se mantiene como proteínas de longitud completa a las que se les permite translocarse al núcleo, donde actúan como activadores (GliA) de la transcripción. Al reducir la expresión de Gli, los factores de transcripción HD reducen la cantidad total de Gli (GliT), por lo que una mayor proporción de GliT se puede estabilizar como GliA para la misma concentración de Shh.

Inmunología

Hay algunas evidencias de que las células T presentan histéresis, ya que se necesita un umbral de señal más bajo para activar las células T que han sido activadas previamente. La activación de la GTPasa Ras es necesaria para las funciones efectoras posteriores de las células T activadas. [32] La activación del receptor de células T induce altos niveles de activación de Ras, lo que da como resultado niveles más altos de Ras unido a GTP (activo) en la superficie celular. Dado que se han acumulado niveles más altos de Ras activo en la superficie celular en las células T que han sido estimuladas previamente por una fuerte interacción del receptor de células T, las señales más débiles del receptor de células T posteriores recibidas poco después proporcionarán el mismo nivel de activación debido a la presencia de niveles más altos de Ras ya activado en comparación con una célula ingenua.

Neurociencia

La propiedad por la cual algunas neuronas no vuelven a sus condiciones basales desde una condición estimulada inmediatamente después de la eliminación del estímulo es un ejemplo de histéresis.

Neuropsicología

La neuropsicología , al explorar los correlatos neuronales de la conciencia , interactúa con la neurociencia, aunque la complejidad del sistema nervioso central es un desafío para su estudio (es decir, su funcionamiento resiste una fácil reducción ). La memoria dependiente del contexto y la memoria dependiente del estado muestran aspectos histéricos de la neurocognición .

Fisiología respiratoria

La histéresis pulmonar es evidente al observar la compliancia de un pulmón en la inspiración frente a la espiración. La diferencia en compliancia (Δvolumen/Δpresión) se debe a la energía adicional necesaria para superar las fuerzas de tensión superficial durante la inspiración para reclutar e inflar alvéolos adicionales. [33]

La curva de presión transpulmonar frente al volumen de la inhalación es diferente de la curva de presión frente al volumen de la exhalación; la diferencia se describe como histéresis. El volumen pulmonar a cualquier presión dada durante la inhalación es menor que el volumen pulmonar a cualquier presión dada durante la exhalación. [34]

Fisiología de la voz y del habla

Se puede observar un efecto de histéresis en el inicio de la voz frente al final. [35] El valor umbral de la presión subglótica necesaria para iniciar la vibración de las cuerdas vocales es inferior al valor umbral en el que se detiene la vibración, cuando otros parámetros se mantienen constantes. En las emisiones de secuencias vocal-consonante sorda-vocal durante el habla, la presión intraoral es menor en el inicio de la voz de la segunda vocal en comparación con el final de la voz de la primera vocal, el flujo de aire oral es menor, la presión transglótica es mayor y el ancho glótico es menor.

Ecología y epidemiología

La histéresis es un fenómeno común en ecología y epidemiología, donde el equilibrio observado de un sistema no se puede predecir basándose únicamente en variables ambientales, sino que también requiere conocimiento de la historia pasada del sistema. Ejemplos notables incluyen la teoría de los brotes de gusanos del capullo del abeto y los efectos del comportamiento en la transmisión de enfermedades. [36]

Se examina comúnmente en relación con transiciones críticas entre tipos de ecosistemas o comunidades en las que los competidores dominantes o paisajes enteros pueden cambiar de una manera en gran medida irreversible. [37] [38]

En la ciencia oceánica y climática

Los modelos complejos de océanos y clima se basan en este principio. [39] [40]

En economía

Los sistemas económicos pueden presentar histéresis. Por ejemplo, el desempeño de las exportaciones está sujeto a fuertes efectos de histéresis: debido a los costos fijos de transporte, puede ser necesario un gran impulso para que un país inicie sus exportaciones, pero una vez que se realiza la transición, puede que no se requiera mucho para mantenerlas.

Cuando un shock negativo reduce el empleo en una empresa o industria, quedan menos trabajadores empleados. Como normalmente los trabajadores empleados tienen el poder de fijar los salarios, su reducido número los incentiva a negociar salarios más altos cuando la economía vuelva a mejorar en lugar de dejar que el salario se mantenga en el nivel de equilibrio , donde la oferta y la demanda de trabajadores coincidirían. Esto causa histéresis: el desempleo se vuelve permanentemente más alto después de los shocks negativos. [41] [42]

Desempleo permanentemente más alto

La idea de histéresis se utiliza ampliamente en el área de la economía laboral, específicamente con referencia a la tasa de desempleo . [43] Según las teorías basadas en la histéresis, las recesiones económicas severas y/o el estancamiento persistente (crecimiento lento de la demanda, generalmente después de una recesión) hacen que los individuos desempleados pierdan sus habilidades laborales (comúnmente desarrolladas en el trabajo) o descubran que sus habilidades se han vuelto obsoletas, o se desmotivan, desilusionan o deprimen o pierden habilidades para buscar trabajo. Además, los empleadores pueden usar el tiempo pasado en el desempleo como una herramienta de selección, es decir, para eliminar a los empleados menos deseados en las decisiones de contratación. Luego, en tiempos de auge económico, recuperación o "auge", los trabajadores afectados no compartirán la prosperidad, permaneciendo desempleados durante largos períodos (por ejemplo, más de 52 semanas). Esto hace que el desempleo sea "estructural", es decir, extremadamente difícil de reducir simplemente aumentando la demanda agregada de productos y mano de obra sin causar un aumento de la inflación. Es decir, es posible que exista un efecto de trinquete en las tasas de desempleo, de modo que un aumento de corto plazo de las tasas de desempleo tienda a persistir. Por ejemplo, la política antiinflacionaria tradicional (el uso de la recesión para combatir la inflación) conduce a una tasa "natural" de desempleo permanentemente más alta (más científicamente conocida como NAIRU ). Esto ocurre, en primer lugar, porque las expectativas inflacionarias son " rígidas " a la baja debido a las rigideces de los salarios y los precios (y, por lo tanto, se adaptan lentamente con el tiempo en lugar de ser aproximadamente correctas como en las teorías de las expectativas racionales ) y, en segundo lugar, porque los mercados laborales no se equilibran instantáneamente en respuesta al desempleo.

La existencia de la histéresis se ha propuesto como una posible explicación del desempleo persistentemente alto de muchas economías en la década de 1990. Olivier Blanchard, entre otros, ha invocado la histéresis para explicar las diferencias en las tasas de desempleo de largo plazo entre Europa y los Estados Unidos. Por lo tanto, la reforma del mercado laboral (que generalmente significa un cambio institucional que promueva salarios más flexibles, despidos y contrataciones) o un fuerte crecimiento económico del lado de la demanda no pueden reducir este grupo de desempleados de largo plazo. Por lo tanto, los programas de capacitación específicos se presentan como una posible solución de política. [41] Sin embargo, la hipótesis de la histéresis sugiere que dichos programas de capacitación se ven favorecidos por una demanda persistentemente alta de productos (quizás con políticas de ingresos para evitar un aumento de la inflación), lo que reduce más fácilmente los costos de transición del desempleo al empleo remunerado.

Modelos

Los modelos histeréticos son modelos matemáticos capaces de simular comportamientos no lineales complejos (histéresis) que caracterizan los sistemas mecánicos y los materiales utilizados en diferentes campos de la ingeniería , como la aeroespacial , la civil y la mecánica . Algunos ejemplos de sistemas mecánicos y materiales que presentan comportamiento histerético son:

  • materiales como acero , hormigón armado , madera ;
  • elementos estructurales, como juntas de acero, hormigón armado o madera;
  • dispositivos, como aisladores sísmicos [44] y amortiguadores.

Cada tema que involucra histéresis tiene modelos que son específicos del tema. Además, hay modelos histeréticos que capturan características generales de muchos sistemas con histéresis. [45] [46] [47] Un ejemplo es el modelo de histéresis de Preisach , que representa una no linealidad de histéresis como una superposición lineal de bucles cuadrados llamados relés no ideales. [45] Muchos modelos complejos de histéresis surgen de la simple conexión paralela, o superposición, de portadores elementales de histéresis denominados histerones.

En el modelo de Lapshin se puede encontrar una descripción paramétrica sencilla e intuitiva de varios bucles de histéresis. [46] [47] Junto con los bucles suaves, la sustitución de pulsos trapezoidales, triangulares o rectangulares en lugar de las funciones armónicas permite construir en el modelo bucles de histéresis lineales por partes que se utilizan con frecuencia en automatismos discretos. Existen implementaciones del modelo de bucle de histéresis en Mathcad [47] y en el lenguaje de programación R. [48]

El modelo de histéresis de Bouc-Wen se utiliza a menudo para describir sistemas histeréticos no lineales. Fue introducido por Bouc [49] [50] y ampliado por Wen [51] , quien demostró su versatilidad al producir una variedad de patrones histeréticos. Este modelo es capaz de capturar en forma analítica, una gama de formas de ciclos histeréticos que coinciden con el comportamiento de una amplia clase de sistemas histeréticos; por lo tanto, dada su versatilidad y manejabilidad matemática, el modelo de Bouc-Wen ha ganado popularidad rápidamente y se ha ampliado y aplicado a una amplia variedad de problemas de ingeniería, incluidos sistemas de múltiples grados de libertad (MDOF), edificios, marcos, respuesta bidireccional y torsional de sistemas histeréticos, continuos bidimensionales y tridimensionales, y licuefacción del suelo , entre otros. El modelo Bouc-Wen y sus variantes/extensiones se han utilizado en aplicaciones de control estructural , en particular en el modelado del comportamiento de amortiguadores magnetorreológicos , dispositivos de aislamiento de base para edificios y otros tipos de dispositivos de amortiguación; también se ha utilizado en el modelado y análisis de estructuras construidas de hormigón armado, acero, mampostería y madera. [ cita requerida ] . La extensión más importante del modelo Bouc-Wen fue realizada por Baber y Noori y más tarde por Noori y colaboradores. Ese modelo extendido, llamado BWBN, puede reproducir el complejo fenómeno de pinzamiento por corte o deslizamiento-bloqueo que el modelo anterior no podía reproducir. El modelo BWBN se ha utilizado ampliamente en un amplio espectro de aplicaciones y las implementaciones están disponibles en software como OpenSees .

Los modelos histeréticos pueden tener un desplazamiento generalizado como variable de entrada y una fuerza generalizada como variable de salida, o viceversa. En particular, en los modelos histeréticos independientes de la velocidad, la variable de salida no depende de la velocidad de variación de la variable de entrada. [52] [53] tú {\estilo de visualización u} F {\estilo de visualización f}

Los modelos histeréticos independientes de la velocidad se pueden clasificar en cuatro categorías diferentes según el tipo de ecuación que se necesita resolver para calcular la variable de salida:

  • modelos algebraicos
  • modelos trascendentales
  • modelos diferenciales
  • modelos integrales

Lista de modelos

A continuación se enumeran algunos modelos histeréticos notables, junto con sus campos asociados.

Energía

Cuando la histéresis ocurre con variables extensivas e intensivas , el trabajo realizado en el sistema es el área bajo el gráfico de histéresis.

Véase también

Referencias

  1. ^ Mayergoyz, ID (2003). Modelos matemáticos de histéresis y sus aplicaciones . Ámsterdam: Elsevier. p. xiv. ISBN 978-0-12-480873-7.OCLC 162129543  .
  2. ^ "VII. Sobre la producción de corrientes eléctricas transitorias en conductores de hierro y acero al torcerlos cuando están magnetizados o al magnetizarlos cuando están torcidos". Actas de la Royal Society de Londres . 33 (216–219): 21–23. 1882. doi :10.1098/rspl.1881.0067. S2CID  110895565.
  3. ^ abcd Bertotti, Giorgio (1998). "Cap. 2". Histéresis en el magnetismo: para físicos, científicos de materiales e ingenieros . Academic Press . ISBN 978-0-12-093270-2.
  4. ^ El término se atribuye a Truesdell & Noll 1965 por Visintin 1994, página 13.
  5. ^ Visintin 1994, página 13
  6. ^ Mohammad Al Janaideh, Subhash Rakheja, Chun-Yi Su Una inversión analítica generalizada del modelo Prandtl-Ishlinskii para la compensación de histéresis en el control de microposicionamiento, IEEE/ASME Transactions on Mechatronics, Volumen:16 Número:4, pp 734−744, 15 de julio de 2010
  7. ^ Johnson, R. Colin. «Se creó el memristor del «eslabón perdido»: ¿Hay que reescribir los libros de texto?». EE Times, 30 de abril de 2008. Archivado desde el original el 30 de septiembre de 2012. Consultado el 27 de septiembre de 2011 .
  8. ^ Zifeng Yang; Hirofumi Igarashi; Mathew Martin; Hui Hu (7-10 de enero de 2008). Una investigación experimental sobre la histéresis aerodinámica de un perfil aerodinámico de bajo número de Reynolds (PDF) . 46.ª Reunión y exposición de ciencias aeroespaciales de la AIAA. Reno, Nevada: Instituto Americano de Aeronáutica y Astronáutica. AIAA-2008-0315. Archivado desde el original (PDF) el 2017-08-10 . Consultado el 2012-04-25 .
  9. ^ Holmes, Robert R. Jr. (febrero de 2018). Complejidad de la clasificación de ríos (PDF) . Actas de la Conferencia Internacional sobre Hidráulica Fluvial (Caudal fluvial 2016).
  10. ^ Warnecke, Martin; Jouaneh, Musa (1 de septiembre de 2003). "Compensación de holgura en trenes de engranajes mediante modificación de lazo abierto de la trayectoria de entrada". Journal of Mechanical Design . 125 (3): 620–624. doi :10.1115/1.1596241.
  11. ^ Love, Augustus E. (1927). Tratado sobre la teoría matemática de la elasticidad (Dover Books on Physics & Chemistry) . Nueva York: Dover Publications. ISBN 978-0-486-60174-8.
  12. ^ Ewing, JA (1889). "Sobre la histéresis en la relación entre la deformación y el esfuerzo". British Association Reports : 502.
  13. ^ Hopkinson, B.; Williams, GT (1912). "La histéresis elástica del acero". Actas de la Royal Society . 87 (598): 502. Bibcode :1912RSPSA..87..502H. doi : 10.1098/rspa.1912.0104 .
  14. ^ ab Chandran Suja, V.; Frostad, JM; Fuller, GG (31 de octubre de 2016). "Impacto de la compresibilidad en el control de los tensiómetros de presión de burbuja". Langmuir . 32 (46): 12031–12038. doi :10.1021/acs.langmuir.6b03258. ISSN  0743-7463. PMID  27798833.
  15. ^ Alvarez, Nicolas J.; Walker, Lynn M.; Anna, Shelley L. (17 de agosto de 2010). "Un microtensiómetro para investigar el efecto del radio de curvatura en el transporte de surfactante a una interfaz esférica". Langmuir . 26 (16): 13310–13319. doi :10.1021/la101870m. ISSN  0743-7463. PMID  20695573.
  16. ^ Gregg, SJ; Sing, Kenneth SW (1982). Adsorción, área superficial y porosidad (segunda edición). Londres: Academic Press . ISBN 978-0-12-300956-2.
  17. ^ Sing, KSW; Everett, DH; Haul, RAW; Moscou, L.; Pierotti, RA; J. Roquérol, J.; Siemieniewska, T. (1985). "Informe de datos de fisisorción para sistemas gas/sólido con especial referencia a la determinación del área superficial y la porosidad (Recomendaciones 1984)". Química Pura y Aplicada . 57 (4): 603–619. doi : 10.1351/pac198557040603 . S2CID  14894781.
  18. ^ Tompsett, GA; Krogh, L.; Griffin, DW; Conner, WC (2005). "Histéresis y comportamiento de escaneo de tamices moleculares mesoporosos". Langmuir . 21 (8): 8214–8225. doi :10.1021/la050068y. PMID  16114924.
  19. ^ Parkes, Martin (8 de abril de 1999). "Asunto: Precisión de la capacitancia de la humedad del suelo..." SOWACS (Lista de correo). Archivado desde el original el 28 de septiembre de 2011. Consultado el 28 de septiembre de 2011 .
  20. ^ Scanlon, Bridget R .; Andraski, Brian J.; Bilskie, Jim (2002). "3.2.4 Métodos diversos para medir el potencial hídrico o matricial" (PDF) . Métodos de análisis de suelos: Parte 4 Métodos físicos . Serie de libros de la SSSA. Sociedad de Ciencias del Suelo de Estados Unidos. págs. 643–670. doi :10.2136/sssabookser5.4.c23. ISBN. 978-0-89118-893-3. S2CID  102411388. Archivado desde el original (PDF) el 13 de marzo de 2006. Consultado el 26 de mayo de 2006 .
  21. ^ Chikazumi 1997, Capítulo 1
  22. ^ Chikazumi 1997, Capítulo 15
  23. ^ Monod, P.; PréJean, JJ; Tissier, B. (1979). "Histéresis magnética de CuMn en el estado de vidrio de espín". J. Appl. Phys . 50 (B11): 7324. Bibcode :1979JAP....50.7324M. doi :10.1063/1.326943.
  24. ^ Vincent Francois-Lavet y otros (14 de noviembre de 2011). Modelo de histéresis consistente no conservadora incremental vectorial.
  25. ^ Pomerening, Joseph R.; Sontag, Eduardo D.; Ferrell, James E. (2003). "Construcción de un oscilador del ciclo celular: histéresis y biestabilidad en la activación de Cdc2". Nature Cell Biology . 5 (4): 346–251. doi :10.1038/ncb954. PMID  12629549. S2CID  11047458.
  26. ^ Ferrell JE Jr.; Machleder EM (1998). "La base bioquímica de un cambio de destino celular de tipo todo o nada en los ovocitos de Xenopus". Science . 280 (5365): 895–8. Bibcode :1998Sci...280..895F. doi :10.1126/science.280.5365.895. PMID  9572732.
  27. ^ Doncic, Andreas; Skotheim, Jan M (2013). "La regulación de avance garantiza la estabilidad y la rápida reversibilidad de un estado celular". Molecular Cell . 50 (6): 856–68. doi :10.1016/j.molcel.2013.04.014. PMC 3696412 . PMID  23685071. 
  28. ^ Darlington, CD (1937). Avances recientes en citología (genes, células y organismos) (segunda edición). P. Blakiston's Son & Co. ISBN 978-0-8240-1376-9.
  29. ^ Rieger, R.; Michaelis, A.; MM (1968). Glosario de genética y citogenética: clásica y molecular (tercera edición). Springer . ISBN 978-3-540-04316-4.
  30. ^ Harfe, BD; Scherz, PJ; Nissim, S.; Tian, ​​H.; McMahon, AP; Tabin, CJ (2004). "Evidencia de un gradiente temporal Shh basado en la expansión en la especificación de identidades de dígitos de vertebrados". Cell . 118 (4): 517–28. doi : 10.1016/j.cell.2004.07.024 . PMID  15315763. S2CID  16280983.
  31. ^ Lek, M.; Dias, JM; Marklund, U.; Uhde, CW; Kurdija, S.; Lei, Q.; Sussel, L.; Rubenstein, JL; Matise, MP; Arnold, H. -H.; Jessell, TM; Ericson, J. (2010). "Un circuito de retroalimentación de homeodominio subyace a la interpretación de la función escalonada de un gradiente de morfógeno Shh durante la formación de patrones neuronales ventrales". Desarrollo . 137 (23): 4051–4060. doi : 10.1242/dev.054288 . PMID  21062862.
  32. ^ Das, J.; Ho, M.; Zikherman, J.; Govern, C.; Yang, M.; Weiss, A.; Chakraborty, AK; Roose, JP (2009). "La señalización digital y la histéresis caracterizan la activación de Ras en células linfoides". Cell . 136 (2): 337–351. doi :10.1016/j.cell.2008.11.051. PMC 2662698 . PMID  19167334. 
  33. ^ Escolar, JD; Escolar, A. (2004). "Histéresis pulmonar: una visión morfológica" (PDF) . Histología e histopatología Biología celular y molecular . 19 (1): 159–166. PMID  14702184 . Consultado el 1 de marzo de 2011 .
  34. ^ West, John B. (2005). Fisiología respiratoria: aspectos esenciales . Hagerstown, MD: Lippincott Williams & Wilkins . ISBN 978-0-7817-5152-0.
  35. ^ Lucero, Jorge C. (1999). "Un estudio teórico del fenómeno de histéresis en el inicio y fin de la oscilación de las cuerdas vocales". Revista de la Sociedad Acústica de América . 105 (1): 423–431. Bibcode :1999ASAJ..105..423L. doi :10.1121/1.424572. ISSN  0001-4966. PMID  9921668.
  36. ^ Strogatz, Stephen H. (1994). Dinámica no lineal y caos . Perseus Books Publishing. Págs. 73-79. ISBN. 0-7382-0453-6.
  37. ^ Sternberg, Leonel Da Silveira Lobo (21 de diciembre de 2001). "Histéresis sabana-bosque en los trópicos". Ecología Global y Biogeografía . 10 (4): 369–378. Código Bib : 2001GloEB..10..369D. doi :10.1046/j.1466-822X.2001.00243.x.
  38. ^ Beisner, BE; Haydon, DT; Cuddington, K (1 de septiembre de 2003). "Estados estables alternativos en ecología". Fronteras en ecología y medio ambiente . 1 (7): 376–382. doi : 10.2307/3868190 . JSTOR  3868190.
  39. ^ Hofmann, Matthias; Rahmstorf, Stefan (8 de diciembre de 2009). "Sobre la estabilidad de la circulación de retorno meridional atlántica". Actas de la Academia Nacional de Ciencias de los Estados Unidos de América . 106 (49): 20584–20589. doi : 10.1073/pnas.0909146106 . ISSN  0027-8424. PMC 2791639 . PMID  19897722. 
  40. ^ Das, Moupriya; Kantz, Holger (29 de junio de 2020). "Resonancia estocástica e histéresis en el clima con fluctuaciones dependientes del estado". Physical Review E . 101 (6): 062145. Bibcode :2020PhRvE.101f2145D. doi :10.1103/PhysRevE.101.062145. ISSN  2470-0045. PMID  32688620.
  41. ^ ab Ball, Laurence M. (marzo de 2009). "Histéresis en el desempleo: evidencia antigua y nueva". Documento de trabajo del NBER n.º 14818. doi : 10.3386 /w14818 .
  42. ^ Blanchard, Olivier J.; Summers, Lawrence H. (1986). "Histéresis y el problema del desempleo europeo". NBER Macroeconomics Annual . 1 : 15–78. doi : 10.2307/3585159 . JSTOR  3585159.
  43. ^ SP Hargreaves Heap (1980). "Elegir la tasa 'natural' equivocada: ¿Acelerar la inflación o desacelerar el empleo y el crecimiento?", The Economic Journal, vol. 90, núm. 359 (septiembre de 1980), págs. 611-620. JSTOR  2231931
  44. ^ Vaiana, Nicolò; Spizzuoco, Mariacristina; Serino, Giorgio (junio de 2017). "Aisladores de cable de acero para estructuras ligeras con aislamiento sísmico: caracterización experimental y modelado matemático". Estructuras de ingeniería . 140 : 498–514. Bibcode :2017EngSt.140..498V. doi :10.1016/j.engstruct.2017.02.057.
  45. ^ ab Mayergoyz, Isaak D. (2003). Modelos matemáticos de histéresis y sus aplicaciones: segunda edición (electromagnetismo) . Academic Press . ISBN 978-0-12-480873-7.
  46. ^ ab RV Lapshin (1995). "Modelo analítico para la aproximación del bucle de histéresis y su aplicación al microscopio de efecto túnel" (PDF) . Review of Scientific Instruments . 66 (9). EE. UU.: AIP: 4718–4730. arXiv : 2006.02784 . Bibcode :1995RScI...66.4718L. doi :10.1063/1.1145314. ISSN  0034-6748. S2CID  121671951.(La traducción al ruso está disponible).
  47. ^ abc RV Lapshin (2020). "Un modelo paramétrico mejorado para la aproximación de bucles de histéresis". Review of Scientific Instruments . 91 (6). Estados Unidos: AIP: 065106. arXiv : 1701.08070 . Bibcode :2020RScI...91f5106L. doi :10.1063/5.0012931. ISSN  0034-6748. PMID  32611047. S2CID  13489477.
  48. ^ S. Maynes; F. Yang; A. Parkhurst (20 de noviembre de 2013). «Histéresis de paquetes (herramientas para modelar procesos histéricos y elipses dependientes de la velocidad)». R-project . Consultado el 11 de junio de 2020 .
  49. ^ Bouc, R. (1967). "Vibración forzada de sistemas mecánicos con histéresis". Actas de la Cuarta Conferencia sobre Oscilación No Lineal . Praga, Checoslovaquia. pág. 315.
  50. ^ Bouc, R. (1971). "Modèle mathématique d'hystérésis: aplicación aux systèmes à un degré de liberté". Acústica (en francés). 24 : 16–25.
  51. ^ Wen, YK (1976). "Método para vibración aleatoria de sistemas histeréticos". Revista de Ingeniería Mecánica . 102 (2): 249–263.
  52. ^ Dimian, Mihai; Andrei, Petru (4 de noviembre de 2013). Fenómenos impulsados ​​por ruido en sistemas histeréticos . Saltador. ISBN 9781461413745.
  53. ^ Vaiana, Nicolò; Sessa, Salvatore; Rosati, Luciano (enero de 2021). "Una clase generalizada de modelos uniaxiales independientes de la velocidad para simular fenómenos de histéresis mecánica asimétrica". Sistemas mecánicos y procesamiento de señales . 146 : 106984. Bibcode :2021MSSP..14606984V. doi :10.1016/j.ymssp.2020.106984. S2CID  224951872.

Lectura adicional

Busque histéresis en Wikcionario, el diccionario libre.
La histéresis elástica de una cuerda doméstica se examina en Wikiversidad
  • Descripción general del ángulo de contacto Histéresis
  • Modelo de histéresis de Preisach - Códigos Matlab desarrollados por Zs. Szabó
  • Histéresis
  • ¿Qué es la histéresis? Archivado el 4 de septiembre de 2009 en Wayback Machine
  • Sistemas dinámicos con histéresis (página web interactiva)
  • Aplicación de inversión de magnetización (rotación coherente) [ enlace muerto permanente ]
  • Histéresis elástica y bandas de goma
Obtenido de "https://es.wikipedia.org/w/index.php?title=Histéresis&oldid=1255408533"