Contragolpe (ingeniería)

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Backlash» ingeniería – noticias  · periódicos  · libros  · académico  · JSTOR ( febrero de 2010 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En ingeniería mecánica , el juego , a veces llamado holgura , juego o holgura , es una holgura o movimiento perdido en un mecanismo causado por espacios entre las piezas. Puede definirse como "la distancia o ángulo máximo a través del cual cualquier parte de un sistema mecánico puede moverse en una dirección sin aplicar una fuerza o movimiento apreciables a la siguiente parte en la secuencia mecánica". ^{[1] p. 1-8} Un ejemplo, en el contexto de engranajes y trenes de engranajes , es la cantidad de holgura entre los dientes de engranaje acoplados. Se puede ver cuando se invierte la dirección del movimiento y se recupera el movimiento flojo o perdido antes de que se complete la inversión del movimiento. Se puede escuchar en los acoplamientos ferroviarios cuando un tren invierte la dirección. Otro ejemplo es en un tren de válvulas con taqués mecánicos , donde es necesario un cierto rango de holgura para que las válvulas funcionen correctamente.

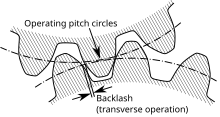
Dependiendo de la aplicación, el juego puede ser deseable o no. Cierta cantidad de juego es inevitable en casi todos los acoplamientos mecánicos reversibles, aunque sus efectos se pueden anular o compensar. En muchas aplicaciones, el ideal teórico sería cero juego, pero en la práctica real se debe permitir cierto juego para evitar atascos. ^{[ cita requerida ]} Las razones para especificar un requisito de juego incluyen permitir lubricación , errores de fabricación, deflexión bajo carga y expansión térmica . ^{[ cita requerida ]} Una causa principal de juego no deseado es el desgaste .

Los factores que afectan la cantidad de juego requerida en un tren de engranajes incluyen errores en el perfil, el paso, el grosor de los dientes, el ángulo de la hélice y la distancia entre centros, y el descentramiento . Cuanto mayor sea la precisión, menor será el juego necesario. El juego se crea más comúnmente cortando los dientes más profundamente en los engranajes que la profundidad ideal. Otra forma de introducir el juego es aumentando las distancias entre centros entre los engranajes. ^[2]

El juego debido a los cambios en el espesor de los dientes generalmente se mide a lo largo del círculo primitivo y se define mediante:

${\displaystyle b_{t}=t_{i}-t_{a}\;}$

dónde:

	$estilo de visualización b_{t}\;}$	= juego debido a modificaciones del espesor de los dientes
	${\displaystyle t_{i}\;}$	= espesor del diente en el círculo primitivo para un engranaje ideal (sin juego)
	${\displaystyle t_{a}\;}$	= espesor real del diente

El juego, medido en el círculo primitivo, debido a las modificaciones del centro de operación se define por: La velocidad de la máquina. El material en la máquina

${\displaystyle b_{c}=2\left(\Delta c\right)\tan \phi }$

dónde:

	$estilo de visualización b_{c}\;}$	= juego debido a modificaciones de la distancia entre centros de operación
	${\displaystyle \Delta c\;}$	= diferencia entre las distancias entre centros operativos reales e ideales
	${\estilo de visualización \phi \;}$	= ángulo de presión

La práctica habitual es dejar margen para la mitad del juego en el espesor de los dientes de cada engranaje. ^{[ cita requerida ]} Sin embargo, si el piñón (el más pequeño de los dos engranajes) es significativamente más pequeño que el engranaje con el que engrana, es una práctica habitual tener en cuenta todo el juego en el engranaje más grande. Esto mantiene la mayor resistencia posible en los dientes del piñón. ^[2] La cantidad de material adicional que se elimina al fabricar los engranajes depende del ángulo de presión de los dientes. Para un ángulo de presión de 14,5°, la distancia adicional en la que se mueve la herramienta de corte es igual a la cantidad de juego deseada. Para un ángulo de presión de 20°, la distancia es igual a 0,73 veces la cantidad de juego deseada. ^[3]

Como regla general, el juego promedio se define como 0,04 dividido por el paso diametral ; el mínimo es 0,03 dividido por el paso diametral y el máximo es 0,05 dividido por el paso diametral . ^[3] En el sistema métrico, puedes simplemente multiplicar los valores con el módulo:

${\displaystyle b_{avg}=0,04*m}$

En un tren de engranajes , el juego es acumulativo. Cuando se invierte el sentido de giro de un tren de engranajes, el engranaje impulsor gira una distancia corta, igual al total de todos los juegos, antes de que el engranaje impulsado final comience a girar. A bajas potencias, el juego genera un cálculo inexacto debido a los pequeños errores que se introducen en cada cambio de dirección; a altas potencias, el juego envía sacudidas a todo el sistema y puede dañar los dientes y otros componentes. ^{[ cita requerida ]}

En ciertas aplicaciones, el juego es una característica indeseable y debe minimizarse.

El mejor ejemplo de esto es el dial de un sintonizador de radio analógico , en el que se pueden realizar movimientos de sintonización precisos tanto hacia adelante como hacia atrás. Los diseños de engranajes especializados lo permiten. Uno de los diseños más comunes divide el engranaje en dos engranajes, cada uno con la mitad del grosor del original.

Una mitad del engranaje está fijada a su eje mientras que la otra mitad del engranaje puede girar sobre el eje, pero precargada en rotación por pequeños resortes helicoidales que hacen girar el engranaje libre con respecto al engranaje fijo. De esta manera, la compresión del resorte hace girar el engranaje libre hasta que se elimina todo el juego del sistema; los dientes del engranaje fijo presionan contra un lado de los dientes del piñón mientras que los dientes del engranaje libre presionan contra el otro lado de los dientes del piñón. Las cargas menores que la fuerza de los resortes no comprimen los resortes y, al no haber espacios entre los dientes que eliminar, se elimina el juego.

Otro ámbito en el que el juego es importante es en los husillos . De nuevo, como en el ejemplo del tren de engranajes, el culpable es la pérdida de movimiento al invertir un mecanismo que se supone que transmite el movimiento con precisión. En lugar de los dientes del engranaje, el contexto son las roscas de los tornillos . Los ejes deslizantes lineales (correderas de la máquina) de las máquinas herramienta son un ejemplo de aplicación.

Durante muchas décadas, la mayoría de las correderas de las máquinas, y muchas incluso hoy en día, han sido superficies de apoyo lineales de hierro fundido simples (pero precisas) , como una corredera de cola de milano o de caja, con un accionamiento por husillo Acme . Con una simple tuerca, es inevitable que se produzca algún contragolpe. En las máquinas herramienta manuales (no CNC ), el medio del maquinista para compensar el contragolpe es acercarse a todas las posiciones precisas utilizando la misma dirección de desplazamiento, es decir, si ha estado marcando a la izquierda y luego quiere moverse a un punto hacia la derecha, se moverá hacia la derecha más allá de él y luego marcará hacia la izquierda de regreso a él; las configuraciones, los acercamientos de las herramientas y las trayectorias de las herramientas deben, en ese caso, diseñarse dentro de esta restricción. ^{[ cita requerida ]}

El siguiente método más complejo que la tuerca simple es una tuerca partida , cuyas mitades se pueden ajustar y bloquear con tornillos, de modo que los dos lados se deslicen, respectivamente, contra la rosca izquierda y el otro lado se deslice hacia las caras derechas. Observe la analogía aquí con el ejemplo del dial de radio que utiliza engranajes partidos, donde las mitades partidas se empujan en direcciones opuestas. A diferencia del ejemplo del dial de radio, la idea de la tensión del resorte no es útil aquí, porque las máquinas herramienta que realizan un corte ejercen demasiada fuerza contra el tornillo. Cualquier resorte lo suficientemente ligero como para permitir el movimiento de la corredera permitiría el traqueteo de la fresa en el mejor de los casos y el movimiento de la corredera en el peor. Estos diseños de tuerca partida ajustada por tornillo en un husillo Acme no pueden eliminar todo el juego en una corredera de máquina a menos que se ajusten tan fuerte que el recorrido comience a trabarse. Por lo tanto, esta idea no puede obviar totalmente el concepto de aproximación siempre desde la misma dirección; Sin embargo, el juego se puede mantener en una cantidad pequeña (1 o 2 milésimas de pulgada o), lo que es más conveniente, y en algunos trabajos no precisos es suficiente para permitir "ignorar" el juego, es decir, diseñar como si no hubiera ninguno. Los CNC se pueden programar para utilizar el concepto de aproximación siempre desde la misma dirección, pero esa no es la forma normal en que se utilizan hoy en día ^{[ ¿cuándo? ]} , porque las tuercas partidas anti-juego hidráulicas y formas más nuevas de husillo que Acme/trapezoidal -como los tornillos de bolas recirculantes- eliminan efectivamente el juego. ^{[ cita requerida ]} El eje puede moverse en cualquier dirección sin el movimiento de pasar y volver.

Los CNC más simples, como los microtornos o las conversiones manuales a CNC, que utilizan accionamientos de tuerca y tornillo Acme, se pueden programar para corregir el juego total en cada eje, de modo que el sistema de control de la máquina se mueva automáticamente la distancia adicional necesaria para compensar la holgura cuando cambia de dirección. Esta "compensación del juego" programática es una solución barata, pero los CNC de nivel profesional utilizan los accionamientos de eliminación del juego más costosos mencionados anteriormente. Esto les permite realizar contorneados en 3D con una fresa de punta esférica, por ejemplo, donde la fresa se desplaza en muchas direcciones con rigidez constante y sin demoras. ^{[ cita requerida ]}

En las computadoras mecánicas se requiere una solución más compleja, es decir, una caja de engranajes de juego frontal. ^[4] Esto funciona girando ligeramente más rápido cuando se invierte la dirección para "usar" el juego.

Algunos controladores de movimiento incluyen compensación de holgura. La compensación se puede lograr simplemente agregando movimiento de compensación adicional (como se describió anteriormente) o detectando la posición de la carga en un esquema de control de bucle cerrado . La respuesta dinámica de la holgura en sí, esencialmente un retraso, hace que el bucle de posición sea menos estable y, por lo tanto, más propenso a la oscilación .

El juego mínimo se calcula como el juego transversal mínimo en el círculo primitivo operativo permitido cuando los dientes del engranaje con el mayor espesor funcional permitido están engranados con los dientes del piñón con su mayor espesor funcional permitido, en la distancia central mínima permitida, en condiciones estáticas.

La variación del juego se define como la diferencia entre el juego máximo y mínimo que se produce en una revolución completa del mayor de un par de engranajes acoplados. ^[5]

El juego en los acoplamientos de engranajes permite una ligera desalineación angular. Puede haber un juego significativo en transmisiones no sincronizadas debido al espacio intencional entre los dientes en los embragues de dientes . El espacio es necesario para acoplar los dientes cuando la velocidad del eje de entrada (motor) y la velocidad del eje de salida (eje de transmisión) están sincronizadas de manera imperfecta. Si hubiera un espacio libre menor, sería casi imposible acoplar los engranajes porque los dientes interferirían entre sí en la mayoría de las configuraciones. En las transmisiones sincronizadas, el sincronizador resuelve este problema.

Sin embargo, el juego no es deseable en aplicaciones de posicionamiento de precisión, como las mesas de máquinas herramienta. Se puede minimizar eligiendo husillos de bolas o husillos con tuercas precargadas y montándolos en cojinetes precargados. Un cojinete precargado utiliza un resorte o un segundo cojinete para proporcionar una fuerza axial de compresión que mantiene las superficies del cojinete en contacto a pesar de la inversión de la dirección de la carga.

• Efecto Bauschinger
• Impulsión armónica
• Histéresis
• Lista de nomenclatura de engranajes