Vidrio giratorio

Física de la materia condensada
Fases Transición de fase PCC
Estados de la materia Sólido Líquido Gas Plasma Condensado de Bose-Einstein Gasolina Bose Condensado fermiónico Gas de Fermi Líquido de Fermi Supersólido Superfluidez Líquido de Luttinger Cristal del tiempo
Fenómenos de fase Parámetro de orden Transición de fase PCC
Fases electrónicas Estructura de banda electrónica Plasma Aislante Aislador Mott Semiconductor Semimetal Conductor Superconductor Termoeléctrico Piezoeléctrico Ferroeléctrico Aislante topológico Semiconductor sin separación de espín
Fenómenos electrónicos Efecto Hall cuántico Efecto Hall de giro Efecto Kondo
Fases magnéticas Diamagnético Superdiamagnético Paramagnético Superparamagnético Ferromagnético Antiferromagnético Metamagnético Vidrio giratorio
Cuasipartículas Fonón Excitón Polaritón plasmónico Polarón Magnón Rotón
Materia blanda Sólido amorfo Coloide Material granular Cristal líquido Polímero
Científicos Van der Waals Onnas de Laue Bragg Débye Bloqueo Ensañador Motón Perlas Landó Luttinger Anderson De Vleck Hubbard Shockley Bardeen Tonelero Schrieffer Josephson Luis Neel Esaki Giaever Kohn Kadanoff Pescador Wilson de Klitzing Binning Tubo Bednorz Müller risa Tormenta Yang Tsui Abrikosov Ginzburgo Leggett Parisi Wetterich Perdew
Portal de física  Categoría
en a mi

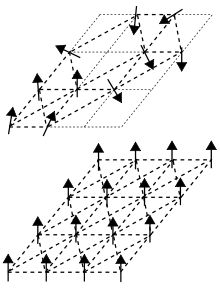
En física de la materia condensada , un vidrio de espín es un estado magnético caracterizado por la aleatoriedad, además de un comportamiento cooperativo en la congelación de espines a una temperatura llamada "temperatura de congelación" T _f . ^[1] En los sólidos ferromagnéticos , los espines magnéticos de los átomos componentes se alinean todos en la misma dirección. El vidrio de espín, en contraste con un ferroimán, se define como un estado magnético " desordenado " en el que los espines están alineados aleatoriamente o sin un patrón regular y los acoplamientos también son aleatorios. ^[1]

El término "vidrio" proviene de una analogía entre el desorden magnético en un vidrio de espín y el desorden posicional de un vidrio químico convencional , por ejemplo, un vidrio de ventana. En el vidrio de ventana o en cualquier sólido amorfo , la estructura de enlace atómico es muy irregular; en contraste, un cristal tiene un patrón uniforme de enlaces atómicos. En los sólidos ferromagnéticos , todos los espines magnéticos se alinean en la misma dirección; esto es análogo a la estructura basada en red de un cristal .

Los enlaces atómicos individuales en un vidrio de espín son una mezcla de cantidades aproximadamente iguales de enlaces ferromagnéticos (donde los vecinos tienen la misma orientación) y enlaces antiferromagnéticos (donde los vecinos tienen exactamente la orientación opuesta: los polos norte y sur están invertidos 180 grados). Estos patrones de imanes atómicos alineados y desalineados crean lo que se conoce como interacciones frustradas  : distorsiones en la geometría de los enlaces atómicos en comparación con lo que se vería en un sólido regular y completamente alineado. También pueden crear situaciones en las que más de una disposición geométrica de átomos es estable.

El vidrio de espín tiene dos aspectos principales. Desde el punto de vista físico, los vidrios de espín son materiales reales con propiedades distintivas, de las que se hace una reseña en este artículo. ^[2] Desde el punto de vista matemático, los modelos de mecánica estadística simples, inspirados en vidrios de espín reales, se estudian y aplican ampliamente. ^[3]

Los vidrios de espín y las complejas estructuras internas que surgen en su interior se denominan " metaestables " porque están "atascados" en configuraciones estables distintas de la configuración de energía más baja (que sería alineada y ferromagnética). La complejidad matemática de estas estructuras es difícil pero fructífera de estudiar experimentalmente o en simulaciones ; con aplicaciones en física, química, ciencia de materiales y redes neuronales artificiales en informática .

Es la dependencia del tiempo lo que distingue a los vidrios de espín de otros sistemas magnéticos.

_{Por encima de la} temperatura de transición vítrea , Tc , ^{[nota 1]} el vidrio de espín exhibe un comportamiento magnético típico (como el paramagnetismo ).

Si se aplica un campo magnético mientras la muestra se enfría hasta la temperatura de transición, la magnetización de la muestra aumenta como se describe en la ley de Curie . Al alcanzar T _c , la muestra se convierte en un vidrio de espín y un enfriamiento adicional produce pocos cambios en la magnetización. Esto se conoce como magnetización enfriada por campo .

Cuando se elimina el campo magnético externo, la magnetización del vidrio de espín cae rápidamente a un valor más bajo conocido como magnetización remanente .

La magnetización luego decae lentamente a medida que se acerca a cero (o a una pequeña fracción del valor original; esto sigue siendo desconocido ). Esta decaimiento no es exponencial y ninguna función simple puede ajustarse adecuadamente a la curva de magnetización en función del tiempo. ^[4] Esta lenta decaimiento es particular de los vidrios de espín. Las mediciones experimentales del orden de días han mostrado cambios continuos por encima del nivel de ruido de la instrumentación. ^[4]

Los vidrios de espín se diferencian de los materiales ferromagnéticos en que, una vez que se elimina el campo magnético externo de una sustancia ferromagnética, la magnetización permanece indefinidamente en el valor remanente. Los materiales paramagnéticos se diferencian de los vidrios de espín en que, una vez que se elimina el campo magnético externo, la magnetización cae rápidamente a cero, sin magnetización remanente. La desintegración es rápida y exponencial. ^{[ cita requerida ]}

Si la muestra se enfría por debajo de Tc en ausencia de un campo magnético externo y se aplica un campo magnético después de la transición a la fase de vidrio de espín, se produce un rápido aumento inicial hasta un valor denominado _{magnetización} enfriada por campo cero . Luego se produce una lenta deriva ascendente hacia la magnetización enfriada por campo.

Sorprendentemente, la suma de las dos funciones complicadas del tiempo (la magnetización remanente y la magnetización enfriada por campo cero) es una constante, es decir, el valor enfriado por campo, y por lo tanto ambas comparten formas funcionales idénticas con el tiempo, ^[5] al menos en el límite de campos externos muy pequeños.

Esto es similar al modelo de Ising . En este modelo, tenemos espines dispuestos en una red de dimensión 1 con solo interacciones de vecinos más cercanos. Este modelo se puede resolver exactamente para las temperaturas críticas y se observa que existe una fase vítrea a bajas temperaturas. ^[6] El hamiltoniano para este sistema de espines está dado por:${\displaystyle d}$

${\displaystyle H=-\sum _{\langle ij\rangle }J_{ij}S_{i}S_{j},}$

donde se refiere a la matriz de espín de Pauli para la partícula de espín-mitad en el punto de red , y la suma sobre se refiere a la suma sobre los puntos de red vecinos y . Un valor negativo de denota una interacción de tipo antiferromagnético entre espines en los puntos y . La suma se extiende sobre todas las posiciones vecinas más cercanas en una red, de cualquier dimensión. Las variables que representan la naturaleza magnética de las interacciones espín-espín se denominan variables de enlace o de enlace.${\displaystyle S_{i}}$${\displaystyle i}$${\displaystyle \langle ij\rangle }$${\displaystyle i}$${\displaystyle j}$${\displaystyle J_{ij}}$${\displaystyle i}$${\displaystyle j}$${\displaystyle J_{ij}}$

Para determinar la función de partición de este sistema, es necesario promediar la energía libre donde , sobre todos los valores posibles de . La distribución de valores de se toma como una distribución gaussiana con una media y una varianza :${\displaystyle f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]}$${\displaystyle {\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)}$${\displaystyle J_{ij}}$${\displaystyle J_{ij}}$${\displaystyle J_{0}}$${\displaystyle J^{2}}$

${\displaystyle P(J_{ij})={\sqrt {\frac {N}{2\pi J^{2}}}}\exp \left\{-{\frac {N}{2J^{2}}}\left(J_{ij}-{\frac {J_{0}}{N}}\right)^{2}\right\}.}$

Al resolver la energía libre utilizando el método de réplica , por debajo de una cierta temperatura, se descubre que existe una nueva fase magnética llamada fase de vidrio de espín (o fase vítrea) del sistema, que se caracteriza por una magnetización que se desvanece junto con un valor que no se desvanece de la función de correlación de dos puntos entre espines en el mismo punto de la red pero en dos réplicas diferentes:${\displaystyle m=0}$

${\displaystyle q=\sum _{i=1}^{N}S_{i}^{\alpha }S_{i}^{\beta }\neq 0,}$

donde son los índices de réplica. Por lo tanto, el parámetro de orden para la transición de fase de ferromagnético a vidrio de espín es , y el de paramagnético a vidrio de espín es nuevamente . Por lo tanto, el nuevo conjunto de parámetros de orden que describe las tres fases magnéticas consta de y .${\displaystyle \alpha ,\beta }$${\displaystyle q}$${\displaystyle q}$${\displaystyle m}$${\displaystyle q}$

Bajo el supuesto de simetría de réplica, la energía libre del campo medio viene dada por la expresión: ^[6]

${\displaystyle {\begin{aligned}\beta f={}-{\frac {\beta ^{2}J^{2}}{4}}(1-q)^{2}+{\frac {\beta J_{0}m^{2}}{2}}-\int \exp \left(-{\frac {z^{2}}{2}}\right)\log \left(2\cosh \left(\beta Jz+\beta J_{0}m\right)\right)\,\mathrm {d} z.\end{aligned}}}$

Además de sus propiedades experimentales inusuales, los vidrios de espín son objeto de extensas investigaciones teóricas y computacionales. Una parte sustancial de los primeros trabajos teóricos sobre los vidrios de espín se ocuparon de una forma de teoría del campo medio basada en un conjunto de réplicas de la función de partición del sistema.

En 1975, David Sherrington y Scott Kirkpatrick introdujeron un importante modelo de vidrio de espín que se puede resolver con exactitud. Se trata de un modelo de Ising con acoplamientos ferromagnéticos y antiferromagnéticos frustrados de largo alcance. Corresponde a una aproximación de campo medio de vidrios de espín que describe la dinámica lenta de la magnetización y el complejo estado de equilibrio no ergódico.

A diferencia del modelo de Edwards-Anderson (EA), en el sistema, aunque solo se consideran interacciones de dos espines, el rango de cada interacción puede ser potencialmente infinito (del orden del tamaño de la red). Por lo tanto, vemos que dos espines cualesquiera pueden estar vinculados con un enlace ferromagnético o antiferromagnético y la distribución de estos se da exactamente como en el caso del modelo de Edwards-Anderson. El hamiltoniano para el modelo SK es muy similar al modelo EA:

${\displaystyle H=-{\frac {1}{\sqrt {N}}}\sum _{i<j}J_{ij}S_{i}S_{j}}$

donde tienen los mismos significados que en el modelo EA. La solución de equilibrio del modelo, después de algunos intentos iniciales de Sherrington, Kirkpatrick y otros, fue encontrada por Giorgio Parisi en 1979 con el método de réplica. El trabajo posterior de interpretación de la solución de Parisi (por M. Mezard , G. Parisi , MA Virasoro y muchos otros) reveló la naturaleza compleja de una fase vítrea de baja temperatura caracterizada por ruptura de ergodicidad, ultrametricidad y no autopromediación. Desarrollos posteriores llevaron a la creación del método de cavidad , que permitió el estudio de la fase de baja temperatura sin réplicas. Una prueba rigurosa de la solución de Parisi se ha proporcionado en el trabajo de Francesco Guerra y Michel Talagrand . ^[7]${\displaystyle J_{ij},S_{i},S_{j}}$

Cuando hay un campo magnético externo uniforme de magnitud , la función de energía se convierte en Sea todos los acoplamientos muestras IID de la distribución gaussiana de media 0 y varianza . En 1979, JRL de Almeida y David Thouless ^[8] encontraron que, como en el caso del modelo de Ising, la solución de campo medio para el modelo SK se vuelve inestable cuando se encuentra en un estado de baja temperatura y bajo campo magnético.${\displaystyle M}$$${\displaystyle H=-{\frac {1}{\sqrt {N}}}\sum _{i<j}J_{ij}S_{i}S_{j}-M\sum _{i}S_{i}}$$${\displaystyle J_{ij}}$${\displaystyle J^{2}}$

La región de estabilidad en el diagrama de fase del modelo SK está determinada por dos parámetros adimensionales . Su diagrama de fase tiene dos partes, divididas por la curva de Almeida-Thouless , La curva es el conjunto de soluciones de las ecuaciones ^[8] La transición de fase ocurre en . Justo debajo de ella, tenemos A baja temperatura, límite de campo magnético alto, la línea es${\displaystyle x:={\frac {kT}{J}},\quad y:={\frac {M}{J}}}$$${\displaystyle {\begin{aligned}&x^{2}={\frac {1}{(2\pi )^{1/2}}}\int \mathrm {d} z\;\mathrm {e} ^{-{\frac {1}{2}}z^{2}}\operatorname {sech} ^{4}\left({\frac {q^{1/2}z+y}{x}}\right),\\&q={\frac {1}{(2\pi )^{1/2}}}\int \mathrm {d} z\;\mathrm {e} ^{-{\frac {1}{2}}z^{2}}\tanh ^{2}\left({\frac {q^{1/2}z+y}{x}}\right).\end{aligned}}}$$${\displaystyle x=1}$$${\displaystyle y^{2}\approx {\frac {4}{3}}(1-x)^{3}.}$$$${\displaystyle x\approx {\frac {4}{3{\sqrt {2\pi }}}}e^{-{\frac {1}{2}}y^{2}}}$$

Este también se denomina "modelo de espín p". ^[3] El modelo de rango infinito es una generalización del modelo de Sherrington-Kirkpatrick, en el que no solo consideramos interacciones de dos espines, sino también interacciones de espín-espín, donde y es el número total de espines. A diferencia del modelo de Edwards-Anderson, pero similar al modelo SK, el rango de interacción es infinito. El hamiltoniano de este modelo se describe mediante:${\displaystyle p}$${\displaystyle p\leq N}$${\displaystyle N}$

${\displaystyle H=-\sum _{i_{1}<i_{2}<\cdots <i_{p}}J_{i_{1}\dots i_{p}}S_{i_{1}}\cdots S_{i_{p}}}$

donde tienen significados similares a los del modelo EA. El límite de este modelo se conoce como el modelo de energía aleatoria . En este límite, la probabilidad de que el vidrio de espín exista en un estado particular depende solo de la energía de ese estado y no de las configuraciones de espín individuales en él. Se supone generalmente que una distribución gaussiana de enlaces magnéticos a través de la red resuelve este modelo. Se espera que cualquier otra distribución dé el mismo resultado, como consecuencia del teorema del límite central . La función de distribución gaussiana, con media y varianza , se da como:${\displaystyle J_{i_{1}\dots i_{p}},S_{i_{1}},\dots ,S_{i_{p}}}$${\displaystyle p\to \infty }$${\displaystyle {\frac {J_{0}}{N}}}$${\displaystyle {\frac {J^{2}}{N}}}$

${\displaystyle P\left(J_{i_{1}\cdots i_{p}}\right)={\sqrt {\frac {N^{p-1}}{J^{2}\pi p!}}}\exp \left\{-{\frac {N^{p-1}}{J^{2}p!}}\left(J_{i_{1}\cdots i_{p}}-{\frac {J_{0}p!}{2N^{p-1}}}\right)\right\}}$

Los parámetros de orden para este sistema están dados por la magnetización y la correlación de espín de dos puntos entre espines en el mismo sitio , en dos réplicas diferentes, que son las mismas que para el modelo SK. Este modelo de rango infinito se puede resolver explícitamente para la energía libre ^[6] en términos de y , bajo el supuesto de simetría de réplica así como de ruptura de simetría de 1-réplica. ^[6]${\displaystyle m}$${\displaystyle q}$${\displaystyle m}$${\displaystyle q}$

${\displaystyle {\begin{aligned}\beta f={}&{\frac {1}{4}}\beta ^{2}J^{2}q^{p}-{\frac {1}{2}}p\beta ^{2}J^{2}q^{p}-{\frac {1}{4}}\beta ^{2}J^{2}+{\frac {1}{2}}\beta J_{0}pm^{p}+{\frac {1}{4{\sqrt {2\pi }}}}p\beta ^{2}J^{2}q^{p-1}+{}\\&\int \exp \left(-{\frac {1}{2}}z^{2}\right)\log \left(2\cosh \left(\beta Jz{\sqrt {{\frac {1}{2}}pq^{p-1}}}+{\frac {1}{2}}\beta J_{0}pm^{p-1}\right)\right)\,\mathrm {d} z\end{aligned}}}$

Un sistema termodinámico es ergódico cuando, dada cualquier instancia (de equilibrio) del sistema, eventualmente visita todos los demás estados (de equilibrio) posibles (de la misma energía). Una característica de los sistemas de vidrio de espín es que, por debajo de la temperatura de congelación , las instancias están atrapadas en un conjunto de estados "no ergódicos": el sistema puede fluctuar entre varios estados, pero no puede pasar a otros estados de energía equivalente. Intuitivamente, se puede decir que el sistema no puede escapar de los mínimos profundos del paisaje energético jerárquicamente desordenado ; las distancias entre los mínimos están dadas por un ultramétrico , con altas barreras de energía entre los mínimos. ^{[nota 2]} La razón de participación cuenta el número de estados a los que se puede acceder desde una instancia dada, es decir, el número de estados que participan en el estado fundamental . El aspecto ergódico del vidrio de espín fue fundamental para la concesión de la mitad del Premio Nobel de Física de 2021 a Giorgio Parisi . ^{[9] [10] [11]}${\displaystyle T_{\text{f}}}$

En el caso de sistemas físicos, como el manganeso diluido en cobre, la temperatura de congelación suele ser tan baja como 30 kelvin (−240 °C), por lo que el magnetismo del vidrio de espín parece carecer prácticamente de aplicaciones en la vida diaria. Sin embargo, los estados no ergódicos y los paisajes energéticos accidentados son bastante útiles para comprender el comportamiento de ciertas redes neuronales , incluidas las redes de Hopfield , así como muchos problemas de optimización informática y genética .

El neodimio cristalino elemental es paramagnético a temperatura ambiente y se convierte en un antiferroimán con un orden desproporcionado al enfriarse por debajo de 19,9 K. ^[12] Por debajo de esta temperatura de transición, exhibe un conjunto complejo de fases magnéticas ^{[13] [14]} que tienen tiempos de relajación de espín largos y un comportamiento de vidrio de espín que no depende del desorden estructural. ^[15]

Se puede encontrar un relato detallado de la historia de los vidrios de espín desde principios de la década de 1960 hasta finales de la década de 1980 en una serie de artículos populares de Philip W. Anderson en Physics Today . ^{[16] [17] [18] [19] [20] [21] [22] [23]}

En la década de 1930, los científicos de materiales descubrieron el efecto Kondo , donde la resistividad del oro nominalmente puro alcanza un mínimo a 10 K, y de manera similar para el Cu nominalmente puro a 2 K. Más tarde se comprendió que el efecto Kondo ocurre cuando un metal no magnético se infunde con átomos magnéticos diluidos.

Se observó un comportamiento inusual en la aleación de hierro en oro (Au Fe ) y la aleación de manganeso en cobre (Cu Mn ) en alrededor de 1 a 10 por ciento atómico . Cannella y Mydosh observaron en 1972 ^[24] que Au Fe tenía un pico inesperado en forma de cúspide en la susceptibilidad a la corriente alterna a una temperatura bien definida, que más tarde se denominaría temperatura de congelación del vidrio de espín . ^[25]

También se lo denominaba "mictomagnet" (micto- es la palabra griega que significa "mixto"). El término surgió de la observación de que estos materiales a menudo contienen una mezcla de interacciones ferromagnéticas ( ) y antiferromagnéticas ( ), lo que conduce a su estructura magnética desordenada. Este término cayó en desuso a medida que evolucionó la comprensión teórica de los vidrios de espín, al reconocerse que la frustración magnética surge no solo de una simple mezcla de interacciones ferromagnéticas y antiferromagnéticas, sino de su aleatoriedad y frustración en el sistema.${\displaystyle J>0}$${\displaystyle J<0}$

Sherrington y Kirkpatrick propusieron el modelo SK en 1975 y lo resolvieron mediante el método de la réplica. ^[26] Descubrieron que a bajas temperaturas, su entropía se vuelve negativa, lo que pensaron que se debía a que el método de la réplica es un método heurístico que no se aplica a bajas temperaturas.

Luego se descubrió que el método de réplica era correcto, pero el problema radica en que la simetría rota a baja temperatura en el modelo SK no se puede caracterizar puramente por el parámetro de orden de Edwards-Anderson. En cambio, son necesarios parámetros de orden adicionales, lo que lleva al ansatz de ruptura de réplica de Giorgio Parisi . En el ansatz de ruptura de réplica completo, se requieren infinitos parámetros de orden para caracterizar una solución estable. ^[27]

El formalismo de la teoría del campo medio de réplica también se ha aplicado en el estudio de redes neuronales , donde ha permitido realizar cálculos de propiedades como la capacidad de almacenamiento de arquitecturas de redes neuronales simples sin necesidad de diseñar o implementar un algoritmo de entrenamiento (como la retropropagación ). ^[28]

También se han estudiado ampliamente modelos de vidrio de espín más realistas con interacciones frustradas de corto alcance y desorden, como el modelo gaussiano, en el que los acoplamientos entre espines vecinos siguen una distribución gaussiana , especialmente mediante simulaciones de Monte Carlo . Estos modelos muestran fases de vidrio de espín bordeadas por transiciones de fase agudas .

Además de su relevancia en la física de la materia condensada, la teoría del vidrio de espín ha adquirido un carácter fuertemente interdisciplinario, con aplicaciones a la teoría de redes neuronales , la informática, la biología teórica, la econofísica , etc.

Los modelos de vidrio de espín se adaptaron al modelo de embudo de plegado del plegamiento de proteínas .

• Stein, Daniel L.; Newman, Charles M. (2013). Vidrios de espín y complejidad . Primers in complex systems. Princeton: Princeton University Press. ISBN 978-0-691-14733-8.Exposición popular, con un mínimo de matemáticas.
• Montanari, Andrea; Sen, Subhabrata (9 de enero de 2024). "Un tutorial fácil de usar sobre técnicas de vidrio de espín de campo medio para no físicos". Fundamentos y tendencias en aprendizaje automático . 17 (1): 1–173. arXiv : 2204.02909 . doi :10.1561/2200000105. ISSN  1935-8237.Una introducción tutorial práctica.
• Mézard, Marc; Montanari, Andrea (2009). Información, física y computación. Oxford, Reino Unido: Oxford University Press. ISBN 9780198570837.OCLC 234430714  .Primeros 15 capítulos de la versión borrador de 2008, disponibles en www.stat.ucla.edu Libro de texto que se centra en el método de cavidad y sus aplicaciones a la informática, especialmente en problemas de satisfacción de restricciones .
• Nishimori, Hidetoshi (2001). Física estadística de vidrios de espín y procesamiento de información: una introducción. Serie internacional de monografías sobre física. Oxford; Nueva York: Oxford University Press. ISBN 978-0-19-850940-0.OCLC 47063323  .Introducción centrada en aplicaciones informáticas, incluidas las redes neuronales.
• Mydosh, JA (1993). Vasos de espín: una introducción experimental . Londres; Washington, DC: Taylor & Francis. ISBN 978-0-7484-0038-6.Se centra en las propiedades medibles experimentalmente de los vidrios de espín (como la aleación de cobre y manganeso).
• Fischer, KH; Hertz, John (1991). Vidrios de espín . Estudios de Cambridge sobre magnetismo. Cambridge; Nueva York, NY, EE. UU.: Cambridge University Press. ISBN 978-0-521-34296-4.Cubre la teoría del campo medio , datos experimentales y simulaciones numéricas.
• Mezard, Marc; Parisi, Giorgio ; Virasoro, Miguel Angel (1987), La teoría del vidrio de espín y más allá , Singapur: World Scientific, ISBN 978-9971-5-0115-0. Exposición temprana que contiene los avances anteriores a 1990, como el truco de la réplica .
• De Dominicis, Cirano; Giardina, Irene (2006). Campos aleatorios y vidrios de espín: un enfoque de teoría de campos. Cambridge, Reino Unido; Nueva York: Cambridge University Press. ISBN 978-0-521-84783-4.OCLC 70764844  .Aproximación mediante la teoría estadística de campos .
• Talagrand, Michel (2010). Modelos de campo medio para gafas de espín. 1: Ejemplos básicos . Ergebnisse der Mathematik und ihrer Grenzgebiete (Repr. de tapa blanda de la tapa dura, 1.ª ed., edición de 2010). Berlín Heidelberg: Springer. ISBN 978-3-642-26598-3.y Talagrand, Michel (2011). Modelos de campo medio para gafas de espín. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge = Una serie de estudios modernos sobre matemáticas. Heidelberg; Nueva York: Springer. ISBN 978-3-642-15201-6.OCLC 733249730  .. Compendio de resultados rigurosamente demostrables.

• Edwards, SF; Anderson, PW (1975), "Teoría de los vidrios de espín", Journal of Physics F: Metal Physics , 5 (5): 965–974, Bibcode :1975JPhF....5..965E, doi :10.1088/0305-4608/5/5/017Captcha de ShieldSquare
• Sherrington, David; Kirkpatrick, Scott (1975), "Modelo resoluble de un vidrio de espín", Physical Review Letters , 35 (26): 1792–1796, Bibcode :1975PhRvL..35.1792S, doi :10.1103/PhysRevLett.35.1792Resumen de Papercore http://papercore.org/Sherrington1975
• Nordblad, P.; Lundgren, L.; Sandlund, L. (1986), "Un vínculo entre la relajación del campo cero enfriado y las magnetizaciones termorremanentes en vidrios de espín", Journal of Magnetism and Magnetic Materials , 54 : 185–186, Bibcode :1986JMMM...54..185N, doi :10.1016/0304-8853(86)90543-3.
• Binder, K. ; Young, AP (1986), "Vidrios de espín: hechos experimentales, conceptos teóricos y preguntas abiertas", Reviews of Modern Physics , 58 (4): 801–976, Bibcode :1986RvMP...58..801B, doi :10.1103/RevModPhys.58.801.
• Bryngelson, Joseph D.; Wolynes, Peter G. (1987), "Vidrios de espín y la mecánica estadística del plegamiento de proteínas", Actas de la Academia Nacional de Ciencias , 84 (21): 7524–7528, Bibcode :1987PNAS...84.7524B, doi : 10.1073/pnas.84.21.7524 , PMC  299331 , PMID  3478708....
• Parisi, G. (1980), "El parámetro de orden para los vidrios de espín: una función en el intervalo 0-1" (PDF) , J. Phys. A: Math. Gen. , 13 (3): 1101–1112, Bibcode :1980JPhA...13.1101P, doi :10.1088/0305-4470/13/3/042Resumen de Papercore http://papercore.org/Parisi1980.
• Talagrand, Michel (2000), "Ruptura de simetría de réplicas y desigualdades exponenciales para el modelo de Sherrington-Kirkpatrick", Annals of Probability , 28 (3): 1018–1062, doi : 10.1214/aop/1019160325 , JSTOR  2652978.
• Guerra, F.; Toninelli, FL (2002), "El límite termodinámico en modelos de vidrio de espín de campo medio", Communications in Mathematical Physics , 230 (1): 71–79, arXiv : cond-mat/0204280 , Bibcode :2002CMaPh.230...71G, doi :10.1007/s00220-002-0699-y, S2CID  16833848

• Estadísticas de frecuencia del término "Spin glass" en arxiv.org