Mecanismo (ingeniería)

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «mecanismo» – noticias  · periódicos  · libros  · académico  · JSTOR ( febrero de 2021 ) ( Aprenda cómo y cuándo eliminar este mensaje )

En ingeniería , un mecanismo es un dispositivo que transforma fuerzas de entrada y movimiento en un conjunto deseado de fuerzas de salida y movimiento. Los mecanismos generalmente constan de componentes móviles que pueden incluir engranajes y trenes de engranajes ; correas y transmisiones por cadena ; levas y seguidores ; eslabones ; dispositivos de fricción, como frenos o embragues ; componentes estructurales como un marco, sujetadores, cojinetes, resortes o lubricantes; varios elementos de máquina , como estrías, pasadores o chavetas.

El científico alemán Franz Reuleaux define la máquina como "una combinación de cuerpos resistentes dispuestos de tal manera que por medio de ellos las fuerzas mecánicas de la naturaleza pueden ser obligadas a realizar un trabajo acompañado de un movimiento determinado". En este contexto, su uso de máquina se interpreta generalmente como mecanismo .

La combinación de fuerza y ​​movimiento define la potencia , y un mecanismo gestiona la potencia para lograr un conjunto deseado de fuerzas y movimientos.

Un mecanismo suele ser una pieza de un proceso más grande, conocido como sistema mecánico o máquina . A veces, se puede hacer referencia a una máquina entera como mecanismo; por ejemplo, el mecanismo de dirección de un automóvil o el mecanismo de cuerda de un reloj de pulsera . Sin embargo, por lo general, se denomina máquina a un conjunto de múltiples mecanismos.

Desde la época de Arquímedes hasta el Renacimiento , los mecanismos se consideraban construidos a partir de máquinas simples , como la palanca , la polea , el tornillo , la rueda y el eje , la cuña y el plano inclinado . Reuleaux se centró en los cuerpos, llamados eslabones , y las conexiones entre estos cuerpos, llamadas pares cinemáticos o articulaciones.

Para estudiar el movimiento de un mecanismo mediante la geometría, sus eslabones se modelan como cuerpos rígidos . Esto significa que se supone que las distancias entre los puntos de un eslabón no cambian a medida que el mecanismo se mueve, es decir, el eslabón no se flexiona. Por lo tanto, se considera que el movimiento relativo entre los puntos de dos eslabones conectados resulta del par cinemático que los une.

Se considera que los pares cinemáticos, o articulaciones, proporcionan restricciones ideales entre dos eslabones, como la restricción de un único punto para rotación pura o la restricción de una línea para deslizamiento puro, así como rodamiento puro sin deslizamiento y contacto puntual con deslizamiento. Un mecanismo se modela como un conjunto de eslabones rígidos y pares cinemáticos.

Reuleaux denominó pares cinemáticos a las conexiones ideales entre eslabones . Distinguió entre pares superiores , con contacto lineal entre los dos eslabones, y pares inferiores , con contacto de área entre los eslabones. J. Phillips ^{[ aclaración necesaria ]} muestra que hay muchas maneras de construir pares que no se ajustan a este modelo simple.

Par inferior: Un par inferior es una unión ideal que tiene contacto superficial entre el par de elementos, como en los siguientes casos:

• Un par giratorio, o articulación articulada, requiere que una línea en el cuerpo móvil permanezca colineal con una línea en el cuerpo fijo, y un plano perpendicular a esta línea en el cuerpo móvil debe mantener contacto con un plano perpendicular similar en el cuerpo fijo. Esto impone cinco restricciones al movimiento relativo de los eslabones, lo que por lo tanto le da al par un grado de libertad.
• Una articulación prismática , o corredera, requiere que una línea en el cuerpo móvil permanezca colineal con una línea en el cuerpo fijo, y un plano paralelo a esta línea en el cuerpo móvil debe mantener contacto con un plano paralelo similar en el cuerpo fijo. Esto impone cinco restricciones al movimiento relativo de los eslabones, lo que por lo tanto le da al par un grado de libertad.
• Una articulación cilíndrica requiere que una línea en el cuerpo móvil permanezca colineal con una línea en el cuerpo fijo. Combina una articulación giratoria y una articulación deslizante. Esta articulación tiene dos grados de libertad.
• Una articulación esférica, o rótula, requiere que un punto del cuerpo móvil mantenga contacto con un punto del cuerpo fijo. Esta articulación tiene tres grados de libertad.
• Una articulación plana requiere que un plano del cuerpo en movimiento mantenga contacto con un plano del cuerpo fijo. Esta articulación tiene tres grados de libertad.
• Una unión de tornillo, o unión helicoidal, solo tiene un grado de libertad porque los movimientos de deslizamiento y rotación están relacionados por el ángulo de hélice de la rosca.

Pares superiores: Generalmente, un par superior es una restricción que requiere un contacto lineal o puntual entre las superficies elementales. Por ejemplo, el contacto entre una leva y su seguidor es un par superior llamado junta de leva . De manera similar, el contacto entre las curvas evolventes que forman los dientes engranados de dos engranajes son juntas de leva.

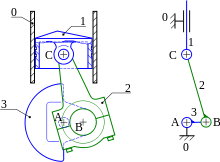
Un diagrama cinemático reduce los componentes de una máquina a un diagrama de esqueleto que enfatiza las articulaciones y reduce los vínculos a elementos geométricos simples. Este diagrama también se puede formular como un gráfico al representar los vínculos del mecanismo como aristas y las articulaciones como vértices del gráfico. Esta versión del diagrama cinemático ha demostrado ser eficaz para enumerar estructuras cinemáticas en el proceso de diseño de máquinas. ^[1]

Una consideración importante en este proceso de diseño es el grado de libertad del sistema de enlaces y uniones, que se determina utilizando el criterio de Chebychev–Grübler–Kutzbach .

Si bien todos los mecanismos de un sistema mecánico son tridimensionales, se pueden analizar utilizando geometría plana si el movimiento de los componentes individuales está restringido de modo que todas las trayectorias puntuales sean paralelas o estén conectadas en serie con un plano. En este caso, el sistema se denomina mecanismo planar . El análisis cinemático de los mecanismos planares utiliza el subconjunto del grupo euclidiano especial SE , que consiste en rotaciones y traslaciones planares, denotado por SE.

El grupo SE es tridimensional, lo que significa que cada posición de un cuerpo en el plano está definida por tres parámetros. Los parámetros suelen ser las coordenadas x e y del origen de un sistema de coordenadas en M , ^{[ aclaración necesaria ]} medidas desde el origen de un sistema de coordenadas en F , y el ángulo medido desde el eje x en F hasta el eje x en M . ^{[ aclaración necesaria ]} Esto se describe a menudo diciendo que un cuerpo en el plano tiene tres grados de libertad .

La rotación pura de una bisagra y la traslación lineal de un deslizador se pueden identificar con subgrupos de SE, y definir las dos articulaciones como articulaciones de un grado de libertad de mecanismos planos. ^{[ incomprensible ]} La articulación de leva formada por dos superficies en contacto deslizante y giratorio es una articulación de dos grados de libertad.

Es posible construir un mecanismo en el que las trayectorias puntuales de todos los componentes se encuentren en capas esféricas concéntricas alrededor de un punto fijo. Un ejemplo es el giroscopio con cardán . Estos dispositivos se denominan mecanismos esféricos. ^[2] Los mecanismos esféricos se construyen conectando eslabones con articulaciones articuladas de modo que los ejes de cada articulación pasen por el mismo punto. Este punto se convierte en el centro de las capas esféricas concéntricas. El movimiento de estos mecanismos se caracteriza por el grupo SO(3) ^{[ aclaración necesaria ]} de rotaciones en el espacio tridimensional. Otros ejemplos de mecanismos esféricos son el diferencial automotriz y la muñeca robótica.

El grupo de rotación SO(3) es tridimensional. Un ejemplo de los tres parámetros que especifican una rotación espacial son los ángulos de balanceo, cabeceo y guiñada que se utilizan para definir la orientación de una aeronave.

Un mecanismo en el que un cuerpo se mueve a través de un movimiento espacial general se denomina mecanismo espacial . Un ejemplo es el enlace RSSR, que puede verse como un enlace de cuatro barras en el que las juntas articuladas del enlace de acoplamiento se reemplazan por extremos de varilla , también llamados juntas esféricas o rótulas . Los extremos de varilla permiten que las bielas de entrada y salida del enlace RSSR se desalineen hasta el punto de que se encuentran en diferentes planos, lo que hace que el enlace de acoplamiento se mueva en un movimiento espacial general. Los brazos robóticos , las plataformas Stewart y los sistemas robóticos humanoides también son ejemplos de mecanismos espaciales.

El mecanismo de Bennett es un ejemplo de un mecanismo espacialmente sobrerrestringido , que se construye a partir de cuatro articulaciones articuladas.

El grupo SE(3) ^{[ aclaración necesaria ]} es hexadimensional, lo que significa que la posición de un cuerpo en el espacio está definida por seis parámetros. Tres de los parámetros definen el origen del sistema de referencia móvil en relación con el sistema fijo. Otros tres parámetros definen la orientación del sistema móvil en relación con el sistema fijo.

Un enlace es una colección de eslabones conectados por articulaciones. Generalmente, los eslabones son los elementos estructurales y las articulaciones permiten el movimiento. Quizás el ejemplo más útil sea el enlace plano de cuatro barras . Sin embargo, existen muchos más enlaces especiales:

• El mecanismo articulado de Watt es un mecanismo articulado de cuatro barras que genera una línea aproximadamente recta. Fue fundamental para el funcionamiento de su diseño de la máquina de vapor. Este mecanismo articulado también aparece en las suspensiones de los vehículos para evitar el movimiento lateral de la carrocería en relación con las ruedas.
• El éxito del mecanismo de Watt condujo al diseño de mecanismos de acoplamiento similares, aproximadamente en línea recta, como el mecanismo de Hoeken y el mecanismo de Chebyshev .
• El mecanismo Peaucellier genera una verdadera salida en línea recta a partir de una entrada rotatoria.
• El enlace Sarrus es un enlace espacial que genera un movimiento en línea recta a partir de una entrada rotatoria.
• El mecanismo de Klann y el mecanismo de Jansen son inventos recientes que permiten realizar movimientos de marcha interesantes. Se trata de un mecanismo de seis y ocho barras, respectivamente.

Un mecanismo flexible es una serie de cuerpos rígidos conectados por elementos flexibles. Estos mecanismos tienen muchas ventajas, entre ellas, un menor número de piezas, una menor "holgura" entre las uniones (no hay movimiento parásito debido a los espacios entre las piezas ^[3] ), almacenamiento de energía, bajo mantenimiento (no requieren lubricación y tienen un bajo desgaste mecánico) y facilidad de fabricación. ^[4]

Los cojinetes de flexión (también conocidos como juntas de flexión ) son un subconjunto de mecanismos flexibles que producen un movimiento geométricamente bien definido (rotación) al aplicar una fuerza.

Un mecanismo de leva y seguidor se forma mediante el contacto directo de dos eslabones de forma especial. El eslabón impulsor se llama leva y el eslabón que se impulsa a través del contacto directo de sus superficies se llama seguidor. La forma de las superficies de contacto de la leva y el seguidor determina el movimiento del mecanismo. En general, la energía de un mecanismo de leva y seguidor se transfiere de leva a seguidor. El árbol de levas gira y, según el perfil de la leva, el seguidor se mueve hacia arriba y hacia abajo. Hoy en día, también existen tipos ligeramente diferentes de seguidores de leva excéntricos, en los que la energía se transfiere del seguidor a la leva. El principal beneficio de este tipo de mecanismo de leva y seguidor es que el seguidor se mueve ligeramente y ayuda a girar la leva seis veces más de longitud de circunferencia con el 70% de la fuerza.

La transmisión de la rotación entre ruedas dentadas en contacto se remonta al mecanismo de Antikythera de Grecia y al carro de guerra chino que apuntaba hacia el sur . Las ilustraciones del científico renacentista Georgius Agricola muestran trenes de engranajes con dientes cilíndricos. La implementación del diente evolvente dio como resultado un diseño de engranaje estándar que proporciona una relación de velocidad constante. Algunas características importantes de los engranajes y los trenes de engranajes son:

• La relación de los círculos primitivos de los engranajes acoplados define la relación de velocidad y la ventaja mecánica del conjunto de engranajes.
• Un tren de engranajes planetarios proporciona una alta reducción de engranajes en un paquete compacto.
• Es posible diseñar dientes de engranaje para engranajes que no sean circulares , pero que aún así transmitan el torque suavemente.
• Las relaciones de velocidad de las transmisiones por cadena y correa se calculan de la misma manera que las relaciones de transmisión .

El diseño de mecanismos para lograr un movimiento y una transmisión de fuerza determinados se conoce como síntesis cinemática de mecanismos . ^[5] Se trata de un conjunto de técnicas geométricas que permiten obtener las dimensiones de eslabones, mecanismos de levas y seguidores, y engranajes y trenes de engranajes para realizar un movimiento mecánico y una transmisión de potencia requeridos. ^[6]

• Tren de engranajes
• Enlace (mecánico)
• Máquina (mecánica)
• Sistema mecánico
• Reloj mecánico
• Esquema de máquinas
• Trabajo virtual
• Mecanismo de Hoberman
• Partes móviles

Wikimedia Commons tiene medios relacionados con Mecanismos (ingeniería) .

• Mecanismo de palanca de bisagra equilibrado
• Wiki de máquinas y mecanismos
• Colecciones de películas y fotografías de cientos de modelos de mecanismos de la Biblioteca Digital de Modelos Cinemáticos para el Diseño (KMODDL)
• Un enlace de línea recta de seis barras en la colección de modelos Reuleaux de la Universidad de Cornell
• Animaciones de una variedad de mecanismos.
• Ejemplo de un generador de funciones de seis barras que calcula el ángulo para un rango determinado
• Una variedad de animaciones de enlaces.
• Una variedad de diseños de varillaje de seis barras
• Animación de un mecanismo desplegable esférico