Viscoelasticidad

Parte de una serie sobre
Mecánica de medios continuos
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ Leyes de difusión de Fick
Leyes Conservaciones Masa Impulso Energía Desigualdades Clausius-Duhem (entropía)
Mecánica de sólidos Deformación Elasticidad lineal Plasticidad Ley de Hooke Estrés Cepa Deformación finita Deformación infinitesimal Compatibilidad Doblado Mecánica de contacto friccional Teoría de la falla del material Mecánica de fracturas
Mecánica de fluidos Fluidos Estática  · Dinámica Principio de Arquímedes  · Principio de Bernoulli Ecuaciones de Navier-Stokes Ecuación de Poiseuille  · Ley de Pascal Viscosidad ( Newtoniano  · no newtoniano ) Flotabilidad  · Mezcla  · Presión Líquidos Adhesión Acción capilar Cromatografía Cohesión (química) Tensión superficial Gases Atmósfera Ley de Boyle Ley de Charles Ley combinada de los gases Ley de Fick Ley de Gay-Lussac Ley de Graham Plasma
Reología Viscoelasticidad Reometría Reómetro Fluidos inteligentes Electrorreológico Magnetoreológico Ferrofluidos
Científicos Bernoulli Niño Cauchy Carlos Euler Mierda Gay-Lussac Graham Gancho Newton Navier No Pascal Estoques Verdadero
en a mi

En la ciencia de los materiales y la mecánica de medios continuos , la viscoelasticidad es la propiedad de los materiales que presentan características viscosas y elásticas cuando sufren deformación . Los materiales viscosos, como el agua, resisten tanto el flujo cortante como la deformación de manera lineal con el tiempo cuando se les aplica una tensión . Los materiales elásticos se deforman cuando se estiran y vuelven inmediatamente a su estado original una vez que se elimina la tensión.

Los materiales viscoelásticos tienen elementos de ambas propiedades y, como tales, presentan una deformación dependiente del tiempo. Mientras que la elasticidad suele ser el resultado del estiramiento de los enlaces a lo largo de los planos cristalográficos en un sólido ordenado, la viscosidad es el resultado de la difusión de átomos o moléculas dentro de un material amorfo . ^[1]

En el siglo XIX, físicos como James Clerk Maxwell , Ludwig Boltzmann y Lord Kelvin investigaron y experimentaron con la fluencia y la recuperación de vidrios , metales y cauchos . La viscoelasticidad se examinó más a fondo a fines del siglo XX cuando se diseñaron polímeros sintéticos y se utilizaron en una variedad de aplicaciones. ^[2] Los cálculos de viscoelasticidad dependen en gran medida de la variable de viscosidad , η . La inversa de η también se conoce como fluidez , φ . El valor de cualquiera de los dos se puede derivar como una función de la temperatura o como un valor dado (es decir, para un amortiguador ). ^[1]

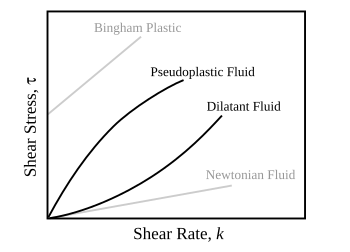
Dependiendo del cambio de la tasa de deformación frente a la tensión dentro de un material, la viscosidad se puede clasificar como de respuesta lineal, no lineal o plástica. Cuando un material exhibe una respuesta lineal se clasifica como material newtoniano . En este caso, la tensión es linealmente proporcional a la tasa de deformación. Si el material exhibe una respuesta no lineal a la tasa de deformación, se clasifica como fluido no newtoniano . También hay un caso interesante en el que la viscosidad disminuye a medida que la tasa de deformación/corte permanece constante. Un material que exhibe este tipo de comportamiento se conoce como tixotrópico . Además, cuando la tensión es independiente de esta tasa de deformación, el material exhibe deformación plástica. ^[1] Muchos materiales viscoelásticos exhiben un comportamiento similar al del caucho , explicado por la teoría termodinámica de la elasticidad de los polímeros.

Algunos ejemplos de materiales viscoelásticos son los polímeros amorfos, los polímeros semicristalinos, los biopolímeros, los metales a temperaturas muy altas y los materiales bituminosos. El agrietamiento se produce cuando la tensión se aplica rápidamente y fuera del límite elástico. Los ligamentos y tendones son viscoelásticos, por lo que el alcance del daño potencial que sufren depende tanto de la velocidad de cambio de su longitud como de la fuerza aplicada. ^{[ cita requerida ]}

Un material viscoelástico tiene las siguientes propiedades:

• La histéresis se observa en la curva de tensión-deformación.
• Se produce relajación del estrés : una tensión constante escalonada provoca una disminución del estrés.
• Se produce fluencia : una tensión constante escalonada provoca un aumento de la deformación.
• Su rigidez depende de la tasa de deformación${\displaystyle {\dot {\varepsilon }}}$ o de la tasa de tensión.${\displaystyle {\dot {\sigma }}}$

A diferencia de las sustancias puramente elásticas, una sustancia viscoelástica tiene un componente elástico y un componente viscoso. La viscosidad de una sustancia viscoelástica le da a la sustancia una dependencia de la velocidad de deformación con el tiempo. Los materiales puramente elásticos no disipan energía (calor) cuando se les aplica una carga y luego se les quita. Sin embargo, una sustancia viscoelástica disipa energía cuando se les aplica una carga y luego se les quita. Se observa histéresis en la curva de tensión-deformación, donde el área del bucle es igual a la energía perdida durante el ciclo de carga. Dado que la viscosidad es la resistencia a la deformación plástica activada térmicamente, un material viscoso perderá energía a través de un ciclo de carga. La deformación plástica da como resultado una pérdida de energía, lo cual no es característico de la reacción de un material puramente elástico a un ciclo de carga. ^[1]

En concreto, la viscoelasticidad es un reordenamiento molecular. Cuando se aplica una tensión a un material viscoelástico, como un polímero , partes de la cadena larga del polímero cambian de posición. Este movimiento o reordenamiento se denomina fluencia . Los polímeros siguen siendo un material sólido incluso cuando estas partes de sus cadenas se reordenan para adaptarse a la tensión y, a medida que esto ocurre, se crea una tensión posterior en el material. Cuando la tensión posterior es de la misma magnitud que la tensión aplicada, el material ya no se fluencia. Cuando se elimina la tensión original, las tensiones posteriores acumuladas harán que el polímero vuelva a su forma original. El material se fluencia, lo que da el prefijo visco-, y el material se recupera por completo, lo que da el sufijo -elasticidad. ^[2]

La viscoelasticidad lineal es cuando la función es separable tanto en la respuesta de fluencia como en la carga. Todos los modelos viscoelásticos lineales se pueden representar mediante una ecuación de Volterra que conecta la tensión y la deformación : o donde $${\displaystyle \varepsilon (t)={\frac {\sigma (t)}{E_{\text{inst,creep}}}}+\int _{0}^{t}K(t-t'){\dot {\sigma }}(t')dt'}$$$${\displaystyle \sigma (t)=E_{\text{inst,relax}}\varepsilon (t)+\int _{0}^{t}F(t-t'){\dot {\varepsilon }}(t')dt'}$$

• Es hora
• ${\displaystyle \sigma (t)}$es estrés
• ${\displaystyle \varepsilon (t)}$es tensión
• ${\displaystyle E_{\text{inst,creep}}}$y son módulos elásticos instantáneos para fluencia y relajación.${\displaystyle E_{\text{inst,relax}}}$
• K ( t ) es lafunción de fluencia
• F ( t ) es la función de relajación

La viscoelasticidad lineal normalmente sólo se aplica para pequeñas deformaciones .

La viscoelasticidad no lineal se produce cuando la función no es separable. Suele ocurrir cuando las deformaciones son grandes o si el material cambia sus propiedades bajo deformaciones. La viscoelasticidad no lineal también esclarece fenómenos observados, como tensiones normales, adelgazamiento por cizallamiento y engrosamiento por extensión en fluidos viscoelásticos. ^[3]

Un material anelástico es un caso especial de material viscoelástico: un material anelástico recuperará completamente su estado original al eliminar la carga.

Al distinguir entre comportamiento elástico, viscoso y formas viscoelásticas, es útil hacer referencia a la escala de tiempo de la medición relativa a los tiempos de relajación del material que se observa, conocido como el número de Deborah (De), donde: ^[3] donde$${\displaystyle De=\lambda /t}$$

• ${\displaystyle \lambda }$es el tiempo de relajación del material
• ${\displaystyle t}$es hora

La viscoelasticidad se estudia mediante análisis mecánico dinámico , aplicando una pequeña tensión oscilatoria y midiendo la deformación resultante.

• Los materiales puramente elásticos tienen tensión y deformación en fase, de modo que la respuesta de una provocada por la otra es inmediata.
• En materiales puramente viscosos, la deformación se retrasa respecto de la tensión en una fase de 90 grados.
• Los materiales viscoelásticos muestran un comportamiento intermedio entre estos dos tipos de materiales y muestran cierto retraso en la deformación.

Se puede utilizar un módulo dinámico complejo G para representar las relaciones entre la tensión y la deformación oscilantes: donde ; es el módulo de almacenamiento y es el módulo de pérdida : donde y son las amplitudes de tensión y deformación respectivamente, y es el desplazamiento de fase entre ellas.$${\displaystyle G=G'+iG''}$$${\displaystyle i^{2}=-1}$${\displaystyle G'}$${\displaystyle G''}$$${\displaystyle G'={\frac {\sigma _{0}}{\varepsilon _{0}}}\cos \delta }$$$${\displaystyle G''={\frac {\sigma _{0}}{\varepsilon _{0}}}\sin \delta }$$${\displaystyle \sigma _{0}}$${\displaystyle \varepsilon _{0}}$${\displaystyle \delta }$

Los materiales viscoelásticos, como los polímeros amorfos, los polímeros semicristalinos, los biopolímeros e incluso los tejidos y células vivos, ^[4] pueden modelarse para determinar sus interacciones de tensión y deformación o fuerza y ​​desplazamiento, así como sus dependencias temporales. Estos modelos, que incluyen el modelo de Maxwell , el modelo de Kelvin-Voigt , el modelo sólido lineal estándar y el modelo de Burgers , se utilizan para predecir la respuesta de un material en diferentes condiciones de carga.

El comportamiento viscoelástico tiene componentes elásticos y viscosos modelados como combinaciones lineales de resortes y amortiguadores , respectivamente. Cada modelo difiere en la disposición de estos elementos, y todos estos modelos viscoelásticos pueden modelarse de manera equivalente como circuitos eléctricos.

En un circuito eléctrico equivalente, la tensión se representa mediante la corriente y la velocidad de deformación mediante el voltaje. El módulo elástico de un resorte es análogo a la inversa de la inductancia de un circuito (almacena energía) y la viscosidad de un amortiguador a la resistencia de un circuito (disipa energía).

Los componentes elásticos, como se mencionó anteriormente, pueden modelarse como resortes de constante elástica E, dada la fórmula: donde σ es la tensión, E es el módulo elástico del material y ε es la deformación que ocurre bajo la tensión dada, similar a la ley de Hooke .$${\displaystyle \sigma =E\varepsilon }$$

Los componentes viscosos se pueden modelar como amortiguadores de modo que la relación tensión-velocidad de deformación se puede dar como, donde σ es la tensión, η es la viscosidad del material y dε/dt es la derivada temporal de la deformación.$${\displaystyle \sigma =\eta {\frac {d\varepsilon }{dt}}}$$

La relación entre tensión y deformación puede simplificarse para tasas de tensión o deformación específicas. Para tasas de tensión o deformación altas/periodos cortos, predominan los componentes de la derivada temporal de la relación tensión-deformación. En estas condiciones, puede aproximarse como una varilla rígida capaz de soportar cargas elevadas sin deformarse. Por lo tanto, el amortiguador puede considerarse un "cortocircuito". ^{[5] [6]}

Por el contrario, para estados de baja tensión y períodos de tiempo más largos, los componentes derivados del tiempo son insignificantes y el amortiguador se puede quitar efectivamente del sistema: un circuito "abierto". ^[6] Como resultado, solo el resorte conectado en paralelo al amortiguador contribuirá a la tensión total en el sistema. ^[5]

El modelo de Maxwell puede representarse mediante un amortiguador puramente viscoso y un resorte puramente elástico conectados en serie, como se muestra en el diagrama. El modelo puede representarse mediante la siguiente ecuación:$${\displaystyle \sigma +{\frac {\eta }{E}}{\dot {\sigma }}=\eta {\dot {\varepsilon }}}$$

Según este modelo, si el material se somete a una tensión constante, las tensiones se relajan gradualmente . Cuando un material se somete a una tensión constante, la tensión tiene dos componentes. En primer lugar, un componente elástico se produce instantáneamente, correspondiente al resorte, y se relaja inmediatamente al liberar la tensión. El segundo es un componente viscoso que crece con el tiempo mientras se aplica la tensión. El modelo de Maxwell predice que la tensión decae exponencialmente con el tiempo, lo que es preciso para la mayoría de los polímeros. Una limitación de este modelo es que no predice la fluencia con precisión. El modelo de Maxwell para la fluencia o las condiciones de tensión constante postula que la tensión aumentará linealmente con el tiempo. Sin embargo, los polímeros en su mayor parte muestran que la tasa de deformación disminuye con el tiempo. ^[2]

Este modelo se puede aplicar a sólidos blandos: polímeros termoplásticos en las proximidades de su temperatura de fusión, hormigón fresco (sin tener en cuenta su envejecimiento) y numerosos metales a una temperatura cercana a su punto de fusión.

Sin embargo, la ecuación introducida aquí carece de una derivación consistente a partir de un modelo más microscópico y no es independiente del observador. El modelo de Maxwell de convección superior es su formulación sólida en términos del tensor de tensión de Cauchy y constituye el modelo constitutivo tensorial más simple para la viscoelasticidad (ver, por ejemplo, ^[7] o ^[6] ).

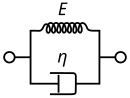
El modelo de Kelvin-Voigt, también conocido como modelo de Voigt, consiste en un amortiguador newtoniano y un resorte elástico de Hooke conectados en paralelo, como se muestra en la imagen. Se utiliza para explicar el comportamiento de fluencia de los polímeros.

La relación constitutiva se expresa como una ecuación diferencial lineal de primer orden:$${\displaystyle \sigma =E\varepsilon +\eta {\dot {\varepsilon }}}$$

Este modelo representa un sólido sometido a una deformación viscoelástica reversible. Al aplicar una tensión constante, el material se deforma a un ritmo decreciente, acercándose asintóticamente a la deformación en estado estacionario. Cuando se libera la tensión, el material se relaja gradualmente hasta su estado no deformado. Con una tensión constante (fluencia), el modelo es bastante realista, ya que predice que la deformación tenderá a σ/E a medida que el tiempo continúa hasta el infinito. De manera similar al modelo de Maxwell, el modelo de Kelvin-Voigt también tiene limitaciones. El modelo es extremadamente bueno para modelar la fluencia en materiales, pero con respecto a la relajación, el modelo es mucho menos preciso. ^[8]

Este modelo se puede aplicar a polímeros orgánicos, caucho y madera cuando la carga no es demasiado alta.

El modelo sólido lineal estándar, también conocido como modelo Zener, consta de dos resortes y un amortiguador. Es el modelo más simple que describe adecuadamente tanto el comportamiento de fluencia como el de relajación de tensiones de un material viscoelástico. Para este modelo, las relaciones constitutivas que rigen son:

Representación de Maxwell	Representación de Kelvin
${\displaystyle \sigma +{\frac {\eta }{E_{2}}}{\dot {\sigma }}=E_{1}\varepsilon +{\frac {\eta (E_{1}+E_{2})}{E_{2}}}{\dot {\varepsilon }}}$	${\displaystyle \sigma +{\frac {\eta }{E_{1}+E_{2}}}{\dot {\sigma }}={\frac {E_{1}E_{2}}{E_{1}+E_{2}}}\varepsilon +{\frac {E_{1}\eta }{E_{1}+E_{2}}}{\dot {\varepsilon }}}$

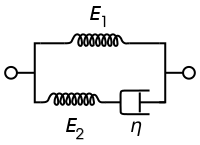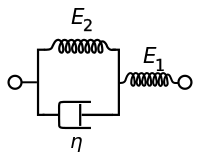Bajo una tensión constante, el material modelado se deformará instantáneamente hasta cierta deformación, que es la parte elástica instantánea de la deformación. Después de eso, continuará deformándose y se acercará asintóticamente a una deformación en estado estable, que es la parte elástica retardada de la deformación. Aunque el modelo sólido lineal estándar es más preciso que los modelos de Maxwell y Kelvin-Voigt para predecir las respuestas del material, matemáticamente arroja resultados inexactos para la deformación en condiciones de carga específicas.

El modelo de Jeffreys, al igual que el modelo Zener, es un modelo de tres elementos. Consta de dos amortiguadores y un resorte. ^[9]

Fue propuesto en 1929 por Harold Jeffreys para estudiar el manto de la Tierra . ^[10]

El modelo de Burgers consta de dos componentes de Maxwell en paralelo o un componente de Kelvin-Voigt, un resorte y un amortiguador en serie. Para este modelo, las relaciones constitutivas que rigen son:

Representación de Maxwell	Representación de Kelvin
${\displaystyle \sigma +\left({\frac {\eta _{1}}{E_{1}}}+{\frac {\eta _{2}}{E_{2}}}\right){\dot {\sigma }}+{\frac {\eta _{1}\eta _{2}}{E_{1}E_{2}}}{\ddot {\sigma }}=\left(\eta _{1}+\eta _{2}\right){\dot {\varepsilon }}+{\frac {\eta _{1}\eta _{2}\left(E_{1}+E_{2}\right)}{E_{1}E_{2}}}{\ddot {\varepsilon }}}$	${\displaystyle \sigma +\left({\frac {\eta _{1}}{E_{1}}}+{\frac {\eta _{2}}{E_{1}}}+{\frac {\eta _{2}}{E_{2}}}\right){\dot {\sigma }}+{\frac {\eta _{1}\eta _{2}}{E_{1}E_{2}}}{\ddot {\sigma }}=\eta _{2}{\dot {\varepsilon }}+{\frac {\eta _{1}\eta _{2}}{E_{1}}}{\ddot {\varepsilon }}}$

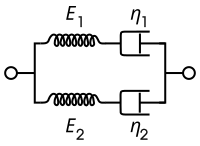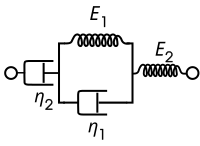Este modelo incorpora flujo viscoso en el modelo sólido lineal estándar, dando como resultado una asíntota linealmente creciente para la deformación en condiciones de carga fijas.

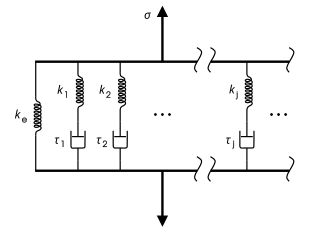
El modelo generalizado de Maxwell, también conocido como modelo de Wiechert, es la forma más general del modelo lineal para la viscoelasticidad. Tiene en cuenta que la relajación no se produce en un único momento, sino en una distribución de momentos. Debido a que los segmentos moleculares tienen longitudes diferentes y los más cortos contribuyen menos que los más largos, existe una distribución temporal variable. El modelo de Wiechert muestra esto al tener tantos elementos de Maxwell de resorte-amortiguador como sean necesarios para representar con precisión la distribución. La figura de la derecha muestra el modelo generalizado de Wiechert. ^[11] Aplicaciones: metales y aleaciones a temperaturas inferiores a un cuarto de su temperatura de fusión absoluta (expresada en K).

Se necesitan ecuaciones constitutivas viscoelásticas no lineales para explicar cuantitativamente fenómenos en fluidos como diferencias en tensiones normales, adelgazamiento por cizallamiento y engrosamiento extensional. ^[3] Necesariamente, la historia experimentada por el material es necesaria para explicar el comportamiento dependiente del tiempo, y normalmente se incluye en los modelos como un núcleo histórico K. ^[12 ]

El fluido de segundo orden se considera típicamente el modelo viscoelástico no lineal más simple y generalmente ocurre en una región estrecha de comportamiento de materiales que ocurre en amplitudes de deformación altas y número de Deborah entre fluidos newtonianos y otros fluidos viscoelásticos no lineales más complicados. ^[3] La ecuación constitutiva del fluido de segundo orden está dada por:

$${\displaystyle \mathbf {T} =-p\mathbf {I} +2\eta _{0}\mathbf {D} -\psi _{1}\mathbf {D} ^{\triangledown }+4\psi _{2}\mathbf {D} \cdot \mathbf {D} }$$

dónde:

• ${\displaystyle \mathbf {I} }$es el tensor identidad
• ${\displaystyle \mathbf {D} }$es el tensor de deformación
• ${\displaystyle \eta _{0},\psi _{1},\psi _{2}}$denotan viscosidad y primer y segundo coeficiente de tensión normal, respectivamente
• ${\displaystyle \mathbf {D} ^{\triangledown }}$denota la derivada convectiva superior del tensor de deformación donde y es la derivada temporal material del tensor de deformación. ^[3]$${\displaystyle \mathbf {D} ^{\triangledown }\equiv {\dot {\mathbf {D} }}-(\nabla \mathbf {v} )^{\mathbf {T} }\cdot \mathbf {D} -\mathbf {D} \cdot \nabla \mathbf {v} }$$${\displaystyle {\dot {\mathbf {D} }}\equiv {\frac {\partial }{\partial t}}\mathbf {D} +\mathbf {v} \cdot \nabla \mathbf {D} }$

El modelo de Maxwell de convección superior incorpora un comportamiento temporal no lineal en el modelo de Maxwell viscoelástico, dado por: ^[3]

$${\displaystyle \mathbf {\tau } +\lambda \mathbf {\tau } ^{\triangledown }=2\eta _{0}\mathbf {D} }$$donde denota el tensor de tensión.${\displaystyle \mathbf {\tau } }$

El modelo Oldroyd-B es una extensión del modelo Maxwell de convección superior y se interpreta como un disolvente lleno de perlas elásticas y mancuernas de resorte. El modelo recibe su nombre de su creador James G. Oldroyd . ^{[13] [14] [15]}

El modelo se puede escribir como: donde:$${\displaystyle \mathbf {T} +\lambda _{1}{\stackrel {\nabla }{\mathbf {T} }}=2\eta _{0}(\mathbf {D} +\lambda _{2}{\stackrel {\nabla }{\mathbf {D} }})}$$

• ${\displaystyle \mathbf {T} }$es el tensor de tensión ;
• ${\displaystyle \lambda _{1}}$es el tiempo de relajación;
• ${\displaystyle \lambda _{2}}$es el tiempo de retardo = ;${\displaystyle {\frac {\eta _{s}}{\eta _{0}}}\lambda _{1}}$
• ${\displaystyle {\stackrel {\nabla }{\mathbf {T} }}}$es la derivada temporal convectiva superior del tensor de tensión:$${\displaystyle {\stackrel {\nabla }{\mathbf {T} }}={\frac {\partial }{\partial t}}\mathbf {T} +\mathbf {v} \cdot \nabla \mathbf {T} -((\nabla \mathbf {v} )^{T}\cdot \mathbf {T} +\mathbf {T} \cdot (\nabla \mathbf {v} ));}$$
• ${\displaystyle \mathbf {v} }$es la velocidad del fluido;
• ${\displaystyle \eta _{0}}$es la viscosidad total compuesta de componentes solventes y polímeros ;${\displaystyle \eta _{0}=\eta _{s}+\eta _{p}}$
• ${\displaystyle \mathbf {D} }$es el tensor de tasa de deformación o tensor de tasa de deformación, .${\displaystyle \mathbf {D} ={\frac {1}{2}}\left[{\boldsymbol {\nabla }}\mathbf {v} +({\boldsymbol {\nabla }}\mathbf {v} )^{T}\right]}$

Si bien el modelo proporciona buenas aproximaciones de fluidos viscoelásticos en flujo de cizallamiento, tiene una singularidad no física en el flujo extensional, donde las pesas se estiran infinitamente. Sin embargo, esto es específico del flujo idealizado; en el caso de una geometría de ranuras cruzadas, el flujo extensional no es ideal, por lo que la tensión, aunque singular, sigue siendo integrable, aunque la tensión sea infinita en una región correspondientemente infinitamente pequeña. ^[15]

Si la viscosidad del disolvente es cero, el Oldroyd-B se convierte en el modelo Maxwell convectivo superior .

El modelo de Wagner puede considerarse una forma práctica simplificada del modelo de Bernstein-Kearsley-Zapas. El modelo fue desarrollado por el reólogo alemán Manfred Wagner .

Para las condiciones isotérmicas el modelo se puede escribir como:$${\displaystyle \mathbf {\sigma } (t)=-p\mathbf {I} +\int _{-\infty }^{t}M(t-t')h(I_{1},I_{2})\mathbf {B} (t')\,dt'}$$

dónde:

• ${\displaystyle \mathbf {\sigma } (t)}$es el tensor de tensión de Cauchy en función del tiempo t ,
• p es la presión
• ${\displaystyle \mathbf {I} }$es el tensor unitario
• M es la función de memoria que muestra, generalmente expresada como una suma de términos exponenciales para cada modo de relajación : donde para cada modo de relajación, es el módulo de relajación y es el tiempo de relajación;$${\displaystyle M(x)=\sum _{k=1}^{m}{\frac {g_{i}}{\theta _{i}}}\exp \left({\frac {-x}{\theta _{i}}}\right),}$$${\displaystyle g_{i}}$${\displaystyle \theta _{i}}$
• ${\displaystyle h(I_{1},I_{2})}$es la función de amortiguación de la deformación que depende de los invariantes primero y segundo del tensor Finger .${\displaystyle \mathbf {B} }$

La función de amortiguación de la deformación se escribe generalmente como: Si el valor de la función de endurecimiento por deformación es igual a uno, entonces la deformación es pequeña; si se acerca a cero, entonces las deformaciones son grandes. ^{[16] [17]}$${\displaystyle h(I_{1},I_{2})=m^{*}\exp(-n_{1}{\sqrt {I_{1}-3}})+(1-m^{*})\exp(-n_{2}{\sqrt {I_{2}-3}})}$$

En una prueba de relajación unidimensional, el material se somete a una deformación repentina que se mantiene constante durante la duración de la prueba, y la tensión se mide a lo largo del tiempo. La tensión inicial se debe a la respuesta elástica del material. Luego, la tensión se relaja con el tiempo debido a los efectos viscosos en el material. Por lo general, se aplica una deformación de tracción, compresión, compresión volumétrica o cizallamiento. Los datos de tensión en función del tiempo resultantes se pueden ajustar con una serie de ecuaciones, llamadas modelos. Solo la notación cambia según el tipo de deformación aplicada: la relajación de tracción-compresión se denota , el cizallamiento se denota , el volumen se denota . La serie de Prony para la relajación de cizallamiento es${\displaystyle E}$${\displaystyle G}$${\displaystyle K}$

$${\displaystyle G(t)=G_{\infty }+\sum _{i=1}^{N}G_{i}\exp(-t/\tau _{i})}$$

donde es el módulo de largo plazo una vez que el material está totalmente relajado, son los tiempos de relajación (que no deben confundirse con en el diagrama); cuanto más altos sean sus valores, más tiempo tarda la tensión en relajarse. Los datos se ajustan a la ecuación utilizando un algoritmo de minimización que ajusta los parámetros ( ) para minimizar el error entre los valores predichos y los datos. ^[18]${\displaystyle G_{\infty }}$${\displaystyle \tau _{i}}$${\displaystyle \tau _{i}}$${\displaystyle G_{\infty },G_{i},\tau _{i}}$

Se obtiene una forma alternativa observando que el módulo elástico está relacionado con el módulo de largo plazo por

$${\displaystyle G(t=0)=G_{0}=G_{\infty }+\sum _{i=1}^{N}G_{i}}$$

Por lo tanto,

$${\displaystyle G(t)=G_{0}-\sum _{i=1}^{N}G_{i}\left[1-e^{-t/\tau _{i}}\right]}$$

Esta forma es conveniente cuando el módulo de corte elástico se obtiene a partir de datos independientes de los datos de relajación, y/o para la implementación en computadora, cuando se desea especificar las propiedades elásticas por separado de las propiedades viscosas, como en Simulia (2010). ^[19]${\displaystyle G_{0}}$

Un experimento de fluencia suele ser más fácil de realizar que uno de relajación, por lo que la mayoría de los datos están disponibles como cumplimiento (de fluencia) frente al tiempo. ^[20] Desafortunadamente, no se conoce una forma cerrada para el cumplimiento (de fluencia) en términos del coeficiente de la serie de Prony. Por lo tanto, si uno tiene datos de fluencia, no es fácil obtener los coeficientes de la serie de Prony (relajación), que se necesitan, por ejemplo, en. ^[19] Una forma conveniente de obtener estos coeficientes es la siguiente. Primero, ajuste los datos de fluencia con un modelo que tenga soluciones de forma cerrada tanto en cumplimiento como en relajación; por ejemplo, el modelo Maxwell-Kelvin (ecuación 7.18-7.19) en Barbero (2007) ^[21] o el Modelo Sólido Estándar (ecuación 7.20-7.21) en Barbero (2007) ^[21] (sección 7.1.3). Una vez conocidos los parámetros del modelo de fluencia, se generan pseudodatos de relajación con el modelo de relajación conjugado para los mismos tiempos de los datos originales. Finalmente, se ajustan los pseudodatos con la serie de Prony.

Los enlaces secundarios de un polímero se rompen y reforman constantemente debido al movimiento térmico. La aplicación de una tensión favorece algunas conformaciones sobre otras, por lo que las moléculas del polímero "fluirán" gradualmente hacia las conformaciones favorecidas con el tiempo. ^[22] Debido a que el movimiento térmico es un factor que contribuye a la deformación de los polímeros, las propiedades viscoelásticas cambian con el aumento o la disminución de la temperatura. En la mayoría de los casos, el módulo de fluencia, definido como la relación entre la tensión aplicada y la deformación dependiente del tiempo, disminuye con el aumento de la temperatura. En términos generales, un aumento de la temperatura se correlaciona con una disminución logarítmica del tiempo necesario para impartir una deformación igual bajo una tensión constante. En otras palabras, se necesita menos trabajo para estirar un material viscoelástico una distancia igual a una temperatura más alta que a una temperatura más baja.

Se puede representar gráficamente un efecto más detallado de la temperatura sobre el comportamiento viscoelástico del polímero como se muestra.

Hay principalmente cinco regiones (algunas denominadas cuatro, que combinan IV y V juntas) incluidas en los polímeros típicos. ^[23]

• Región I: En esta región se presenta el estado vítreo del polímero. La temperatura en esta región para un polímero dado es demasiado baja para otorgarle movimiento molecular. Por lo tanto, el movimiento de las moléculas está congelado en esta área. La propiedad mecánica es dura y quebradiza en esta región. ^[24]
• Región II: El polímero pasa la temperatura de transición vítrea en esta región. Más allá de la Tg, la energía térmica proporcionada por el entorno es suficiente para descongelar el movimiento de las moléculas. Las moléculas pueden tener movimiento local en esta región, lo que conduce a una caída pronunciada de la rigidez en comparación con la Región I.
• Región III: Región de meseta gomosa. Los materiales que se encuentran en esta región existirían con elasticidad de largo alcance impulsada por la entropía. Por ejemplo, una banda de goma está desordenada en el estado inicial de esta región. Al estirar la banda de goma, también se alinea la estructura para que esté más ordenada. Por lo tanto, al soltar la banda de goma, buscará espontáneamente un estado de entropía más alto y, por lo tanto, volverá a su estado inicial. Esto es lo que llamamos recuperación de forma de elasticidad impulsada por la entropía.
• Región IV: El comportamiento en la región de flujo gomoso depende en gran medida del tiempo. Los polímeros en esta región necesitarían utilizar una superposición de tiempo y temperatura para obtener información más detallada para decidir con cautela cómo utilizar los materiales. Por ejemplo, si el material se utiliza para hacer frente a propósitos de tiempo de interacción corto, podría presentarse como un material "duro". Si se utiliza para propósitos de tiempo de interacción largo, actuaría como un material "blando". ^[25]
• Región V: El polímero viscoso fluye fácilmente en esta región. Otra reducción significativa de la rigidez.

Las temperaturas extremadamente frías pueden provocar que los materiales viscoelásticos pasen a la fase vítrea y se vuelvan quebradizos . Por ejemplo, la exposición de los adhesivos sensibles a la presión al frío extremo ( hielo seco , aerosol congelador , etc.) hace que pierdan su adherencia, lo que provoca el desprendimiento.

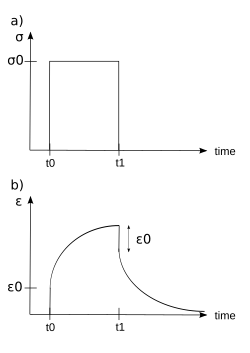
Cuando se someten a una tensión constante escalonada, los materiales viscoelásticos experimentan un aumento de la deformación en función del tiempo. Este fenómeno se conoce como fluencia viscoelástica.

En un tiempo , un material viscoelástico se somete a una tensión constante que se mantiene durante un periodo de tiempo suficientemente largo. El material responde a la tensión con una deformación que aumenta hasta que el material finalmente falla, si es un líquido viscoelástico. Si, por el contrario, es un sólido viscoelástico, puede fallar o no dependiendo de la tensión aplicada frente a la resistencia última del material. Cuando la tensión se mantiene durante un periodo de tiempo más corto, el material sufre una deformación inicial hasta un tiempo , después del cual la deformación disminuye inmediatamente (discontinuidad) y luego disminuye gradualmente a veces hasta una deformación residual.${\displaystyle t_{0}}$${\displaystyle t_{1}}$${\displaystyle t>t_{1}}$

Los datos de fluencia viscoelástica se pueden presentar trazando el módulo de fluencia (tensión aplicada constante dividida por la deformación total en un momento determinado) como una función del tiempo. ^[26] Por debajo de su tensión crítica, el módulo de fluencia viscoelástica es independiente de la tensión aplicada. Una familia de curvas que describen la respuesta de la deformación en función del tiempo a diversas tensiones aplicadas se puede representar mediante una única curva de módulo de fluencia viscoelástica en función del tiempo si las tensiones aplicadas están por debajo del valor de tensión crítica del material.

La fluencia viscoelástica es importante a la hora de considerar el diseño estructural a largo plazo. En función de las condiciones de carga y temperatura, los diseñadores pueden elegir los materiales que mejor se adapten a la vida útil de los componentes.

Los reómetros de corte se basan en la idea de colocar el material que se va a medir entre dos placas, una o ambas de las cuales se mueven en una dirección de corte para inducir tensiones y deformaciones en el material. La prueba se puede realizar a una tasa de deformación constante, tensión o de manera oscilatoria (una forma de análisis mecánico dinámico ). ^[27] Los reómetros de corte suelen estar limitados por los efectos de borde, donde el material puede filtrarse entre las dos placas y deslizarse en la interfaz material/placa.

Los reómetros extensionales, también conocidos como extensiómetros, miden las propiedades viscoelásticas tirando de un fluido viscoelástico, generalmente de manera uniaxial. ^[28] Debido a que esto generalmente hace uso de fuerzas capilares y confina el fluido a una geometría estrecha, la técnica a menudo se limita a fluidos con una viscosidad relativamente baja, como soluciones de polímeros diluidos o algunos polímeros fundidos. ^[28] Los reómetros extensionales también están limitados por los efectos de borde en los extremos del extensiómetro y las diferencias de presión entre el interior y el exterior del capilar. ^[3]

A pesar de las aparentes limitaciones mencionadas anteriormente, la reometría extensional también se puede realizar en fluidos de alta viscosidad. Aunque esto requiere el uso de diferentes instrumentos, estas técnicas y aparatos permiten el estudio de las propiedades viscoelásticas extensionales de materiales como polímeros fundidos. Tres de los instrumentos de reometría extensional más comunes desarrollados en los últimos 50 años son el reómetro de tipo Meissner, el reómetro de estiramiento de filamentos (FiSER) y el reómetro extensional Sentmanat (SER).

El reómetro de tipo Meissner, desarrollado por Meissner y Hostettler en 1996, utiliza dos conjuntos de rodillos contrarrotativos para tensar una muestra uniaxialmente. ^[29] Este método utiliza una longitud de muestra constante durante todo el experimento y sostiene la muestra entre los rodillos mediante un colchón de aire para eliminar los efectos de pandeo de la muestra. Tiene algunos problemas: por un lado, el fluido puede resbalar en las correas, lo que produce tasas de deformación más bajas de lo esperado. Además, este equipo es difícil de operar y costoso de comprar y mantener.

El reómetro FiSER simplemente contiene fluido entre dos placas. Durante un experimento, la placa superior se mantiene firme y se aplica una fuerza a la placa inferior, alejándola de la superior. ^[30] La tasa de deformación se mide por la tasa de cambio del radio de la muestra en su parte media. Se calcula utilizando la siguiente ecuación: donde es el valor del radio medio y es la tasa de deformación. Luego, la viscosidad de la muestra se calcula utilizando la siguiente ecuación: donde es la viscosidad de la muestra y es la fuerza aplicada a la muestra para separarla.$${\displaystyle {\dot {\epsilon }}=-{\frac {2}{R}}{dR \over dt}}$$${\displaystyle R}$${\displaystyle {\dot {\epsilon }}}$$${\displaystyle \eta ={\frac {F}{\pi R^{2}{\dot {\epsilon }}}}}$$${\displaystyle \eta }$${\displaystyle F}$

Al igual que el reómetro de tipo Meissner, el reómetro SER utiliza un conjunto de dos rodillos para deformar una muestra a una velocidad determinada. ^[31] A continuación, calcula la viscosidad de la muestra utilizando la conocida ecuación: donde es la tensión, es la viscosidad y es la velocidad de deformación. La tensión en este caso se determina mediante transductores de par presentes en el instrumento. El pequeño tamaño de este instrumento facilita su uso y elimina la flacidez de la muestra entre los rodillos. A la derecha se puede encontrar un esquema que detalla el funcionamiento del reómetro extensional SER.$${\displaystyle \sigma =\eta {\dot {\epsilon }}}$$${\displaystyle \sigma }$${\displaystyle \eta }$${\displaystyle {\dot {\epsilon }}}$

Aunque existen muchos instrumentos que prueban la respuesta viscoelástica y mecánica de los materiales, la espectroscopia viscoelástica de banda ancha (BVS) y la espectroscopia ultrasónica resonante (RUS) se utilizan con más frecuencia para probar el comportamiento viscoelástico porque se pueden utilizar por encima y por debajo de las temperaturas ambiente y son más específicas para probar la viscoelasticidad. Estos dos instrumentos emplean un mecanismo de amortiguación en varias frecuencias y rangos de tiempo sin recurrir a la superposición de tiempo y temperatura . El uso de BVS y RUS para estudiar las propiedades mecánicas de los materiales es importante para comprender cómo se comportará un material que exhibe viscoelasticidad. ^[32]