Hipérbola


En matemáticas , una hipérbola es un tipo de curva suave que se encuentra en un plano , definida por sus propiedades geométricas o por ecuaciones para las que es el conjunto solución. Una hipérbola tiene dos partes, llamadas componentes o ramas conectadas, que son imágenes especulares una de la otra y se asemejan a dos arcos infinitos . La hipérbola es uno de los tres tipos de sección cónica , formada por la intersección de un plano y un cono doble . (Las otras secciones cónicas son la parábola y la elipse . Un círculo es un caso especial de elipse). Si el plano interseca ambas mitades del cono doble pero no pasa por el vértice de los conos, entonces la cónica es una hipérbola.
Además de ser una sección cónica, una hipérbola puede surgir como el lugar geométrico de puntos cuya diferencia de distancias a dos focos fijos es constante, como una curva para cada punto de la cual los rayos a dos focos fijos son reflexiones a través de la línea tangente en ese punto, o como la solución de ciertas ecuaciones cuadráticas bivariadas como la relación recíproca [1] En aplicaciones prácticas, una hipérbola puede surgir como la trayectoria seguida por la sombra de la punta del gnomon de un reloj de sol , la forma de una órbita abierta como la de un objeto celeste que excede la velocidad de escape del cuerpo gravitacional más cercano, o la trayectoria de dispersión de una partícula subatómica , entre otras.
Cada rama de la hipérbola tiene dos brazos que se van haciendo más rectos (curvatura inferior) a medida que se alejan del centro de la hipérbola. Los brazos diagonalmente opuestos, uno de cada rama, tienden en el límite a una línea común, llamada asíntota de esos dos brazos. Por lo tanto, hay dos asíntotas, cuya intersección está en el centro de simetría de la hipérbola, que puede considerarse como el punto de espejo sobre el que cada rama se refleja para formar la otra rama. En el caso de la curva, las asíntotas son los dos ejes de coordenadas . [1]
Las hipérbolas comparten muchas de las propiedades analíticas de las elipses, como la excentricidad , el foco y la directriz . Normalmente, la correspondencia se puede realizar con nada más que un cambio de signo en algún término. Muchos otros objetos matemáticos tienen su origen en la hipérbola, como los paraboloides hiperbólicos (superficies en forma de silla de montar), los hiperboloides ("cestas de basura"), la geometría hiperbólica ( la célebre geometría no euclidiana de Lobachevsky ), las funciones hiperbólicas (sinh, cosh, tanh, etc.) y los espacios girovectoriales (una geometría propuesta para su uso tanto en la relatividad como en la mecánica cuántica que no es euclidiana ).
Etimología e historia
La palabra hipérbola deriva del griego ὑπερβολή , que significa «sobre-arrojado» o «excesivo», de donde también deriva el término inglés hipérbole . Las hipérbolas fueron descubiertas por Menecmo en sus investigaciones sobre el problema de doblar el cubo , pero entonces se las llamaba secciones de conos obtusos. [2] Se cree que el término hipérbola fue acuñado por Apolonio de Perge ( c. 262 – c. 190 a. C. ) en su obra definitiva sobre las secciones cónicas , las Cónicas . [3] Los nombres de las otras dos secciones cónicas generales, la elipse y la parábola , derivan de las palabras griegas correspondientes para «deficiente» y «aplicada»; los tres nombres son préstamos de la terminología pitagórica anterior que se refería a una comparación del lado de rectángulos de área fija con un segmento de línea dado. El rectángulo podría ser "aplicado" al segmento (es decir, tener una longitud igual), ser más corto que el segmento o exceder el segmento. [4]
Definiciones
Como lugar geométrico de puntos


Una hipérbola se puede definir geométricamente como un conjunto de puntos ( lugar geométrico de puntos ) en el plano euclidiano:
El punto medio del segmento de línea que une los focos se llama centro de la hipérbola. [6] La línea que pasa por los focos se llama eje mayor . Contiene los vértices , que tienen distancia al centro. La distancia de los focos al centro se llama distancia focal o excentricidad lineal . El cociente es la excentricidad .
La ecuación se puede ver de una manera diferente (ver diagrama):
Si es el círculo con punto medio y radio , entonces la distancia de un punto de la rama derecha al círculo es igual a la distancia al foco : se llama directriz circular (relacionada con el foco ) de la hipérbola. [7] [8] Para obtener la rama izquierda de la hipérbola, uno tiene que usar la directriz circular relacionada con . Esta propiedad no debe confundirse con la definición de una hipérbola con ayuda de una directriz (línea) a continuación.
Hipérbola con ecuacióny = A / x


Si el sistema de coordenadas xy se gira alrededor del origen por el ángulo y se asignan nuevas coordenadas , entonces .
La hipérbola rectangular (cuyos semiejes son iguales) tiene la nueva ecuación . Resolviendo para se obtiene
Así, en un sistema de coordenadas xy la gráfica de una función con ecuación es una hipérbola rectangular enteramente en el primer y tercer cuadrantes con
- los ejes de coordenadas como asíntotas ,
- la línea como eje mayor ,
- El centro y el semieje
- Los vértices
- el semi-lato recto y el radio de curvatura en los vértices
- La excentricidad lineal y la excentricidad
- la tangente en el punto
Una rotación de la hipérbola original da como resultado una hipérbola rectangular enteramente en el segundo y cuarto cuadrantes, con las mismas asíntotas, centro, semilato recto, radio de curvatura en los vértices, excentricidad lineal y excentricidad que para el caso de rotación, con ecuación
- los semiejes
- la línea como eje mayor,
- Los vértices
Al desplazar la hipérbola con ecuación de modo que el nuevo centro sea , se obtiene la nueva ecuación y las nuevas asíntotas son y . Los parámetros de forma permanecen inalterados.
Por la propiedad directriz


Las dos rectas alejadas del centro y paralelas al eje menor se llaman directrices de la hipérbola (ver diagrama).
Para un punto arbitrario de la hipérbola, el cociente de la distancia a un foco y a la directriz correspondiente (ver diagrama) es igual a la excentricidad: La prueba para el par se sigue del hecho de que y satisfacen la ecuación El segundo caso se demuestra análogamente.

La afirmación inversa también es verdadera y puede utilizarse para definir una hipérbola (de manera similar a la definición de una parábola):
Para cualquier punto (foco), cualquier recta (directriz) no pasante y cualquier número real con el conjunto de puntos (lugar geométrico de los puntos), para el cual el cociente de las distancias al punto y a la recta es es una hipérbola.
(La elección da como resultado una parábola y si una elipse .)
Prueba
Sea y supongamos que es un punto en la curva. La directriz tiene ecuación . Con , la relación produce las ecuaciones
- y
La sustitución da Esta es la ecuación de una elipse ( ) o una parábola ( ) o una hipérbola ( ). Todas estas cónicas no degeneradas tienen en común el origen como vértice (ver diagrama).
Si , introduzca nuevos parámetros de modo que , y entonces la ecuación anterior se convierte en que es la ecuación de una hipérbola con centro , el eje x como eje mayor y el semieje mayor/menor .
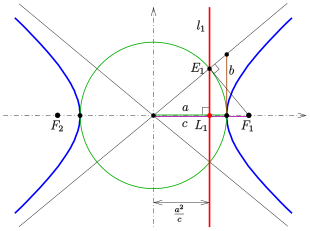
Construcción de una directriz
Debido a que el punto de la directriz (ver diagrama) y el foco son inversos con respecto a la inversión del círculo en el círculo (en el diagrama verde), el punto se puede construir utilizando el teorema de Tales (no se muestra en el diagrama). La directriz es la perpendicular a la línea que pasa por el punto .
Construcción alternativa de : El cálculo muestra que el punto es la intersección de la asíntota con su perpendicular (ver diagrama).
Como sección plana de un cono

La intersección de un cono doble vertical con un plano que no pasa por el vértice y cuya pendiente es mayor que la pendiente de las líneas del cono es una hipérbola (ver diagrama: curva roja). Para demostrar la propiedad definitoria de una hipérbola (ver arriba) se utilizan dos esferas de Dandelin , que son esferas que tocan el cono a lo largo de círculos , y el plano de intersección (hipérbola) en los puntos y . Resulta que: son los focos de la hipérbola.
- Sea un punto arbitrario de la curva de intersección.
- La generatriz del cono que contiene interseca al círculo en el punto y al círculo en un punto .
- Los segmentos de línea y son tangentes a la esfera y, por lo tanto, tienen la misma longitud.
- Los segmentos de línea y son tangentes a la esfera y, por lo tanto, tienen la misma longitud.
- El resultado es: es independiente del punto de la hipérbola , porque no importa dónde se encuentre el punto, debe estar en los círculos , y el segmento de línea debe cruzar el vértice. Por lo tanto, a medida que el punto se mueve a lo largo de la curva roja (hipérbola), el segmento de línea simplemente gira alrededor del vértice sin cambiar su longitud.
Construcción de clavijas y cuerdas

La definición de una hipérbola por sus focos y sus directrices circulares (ver arriba) se puede utilizar para dibujar un arco de la misma con ayuda de alfileres, una cuerda y una regla: [9]
- Elige los focos , los vértices y una de las directrices circulares , por ejemplo (círculo con radio )
- Se fija una regla en un punto que puede girar libremente . El punto está marcado a una distancia de .
- Se prepara una cuerda con longitud .
- Un extremo de la cuerda está fijado en un punto de la regla, el otro extremo está fijado en el punto .
- Tome un bolígrafo y sujete la cuerda firmemente contra el borde de la regla.
- Al girar la regla, el lápiz dibuja un arco de la rama derecha de la hipérbola, debido a (ver la definición de una hipérbola por directrices circulares ).
Generación de Steiner de una hipérbola


El siguiente método para construir puntos individuales de una hipérbola se basa en la generación de Steiner de una sección cónica no degenerada :
Para la generación de puntos de la hipérbola se utilizan los lápices en los vértices . Sea un punto de la hipérbola y . El segmento de recta se divide en n segmentos igualmente espaciados y esta división se proyecta paralelamente con la diagonal como dirección sobre el segmento de recta (ver diagrama). La proyección paralela es parte de la proyección proyectiva entre los lápices en y necesarios. Los puntos de intersección de dos rectas relacionadas y son puntos de la hipérbola definida de forma única.
Observaciones:
- La subdivisión podría extenderse más allá de los puntos y así obtener más puntos, pero la determinación de los puntos de intersección sería más imprecisa. Una mejor idea es extender los puntos ya construidos por simetría (ver animación).
- La generación de Steiner también existe para elipses y parábolas.
- La generación de Steiner a veces se denomina método del paralelogramo porque se pueden utilizar otros puntos en lugar de los vértices, que comienzan con un paralelogramo en lugar de un rectángulo.
Ángulos inscritos para hipérbolasy = a /( x − b ) + cy la forma de 3 puntos

Una hipérbola con ecuación está determinada de forma única por tres puntos con coordenadas x e y diferentes . Una forma sencilla de determinar los parámetros de forma es utilizar el teorema del ángulo inscrito para hipérbolas:
De manera análoga al teorema del ángulo inscrito para círculos se obtiene el
Teorema del ángulo inscrito para hipérbolas [10] [11] — Para cuatro puntos (ver diagrama) la siguiente afirmación es verdadera:
Los cuatro puntos están en una hipérbola con ecuación si y solo si los ángulos en y son iguales en el sentido de la medida anterior. Esto significa que si
La prueba se puede obtener mediante un cálculo sencillo. Si los puntos están en una hipérbola, se puede suponer que la ecuación de la hipérbola es .
Una consecuencia del teorema del ángulo inscrito para las hipérbolas es la
Forma de 3 puntos de la ecuación de una hipérbola : la ecuación de la hipérbola determinada por 3 puntos es la solución de la ecuación para .
Como imagen afín de la hipérbola unitariax2 - y2 = 1

Otra definición de hipérbola utiliza transformaciones afines :
Representación paramétrica
Una transformación afín del plano euclidiano tiene la forma , donde es una matriz regular (su determinante no es 0) y es un vector arbitrario. Si son los vectores columna de la matriz , la hipérbola unitaria se mapea sobre la hipérbola.
es el centro, un punto de la hipérbola y un vector tangente en este punto.
Vértices
En general, los vectores no son perpendiculares. Es decir, en general no son los vértices de la hipérbola, sino que apuntan en las direcciones de las asíntotas. El vector tangente en el punto es Como en un vértice la tangente es perpendicular al eje mayor de la hipérbola, se obtiene el parámetro de un vértice de la ecuación y, por lo tanto, de donde se obtiene
Se utilizaron las fórmulas , , y .
Los dos vértices de la hipérbola son
Representación implícita
Resolviendo la representación paramétrica para mediante la regla de Cramer y utilizando , se obtiene la representación implícita
Hipérbola en el espacio
La definición de hipérbola en esta sección da una representación paramétrica de una hipérbola arbitraria, incluso en el espacio, si se permite que haya vectores en el espacio.
Como imagen afín de la hipérbolay = 1/ x

Como la hipérbola unitaria es afínmente equivalente a la hipérbola , una hipérbola arbitraria puede considerarse como la imagen afín (ver sección anterior) de la hipérbola :
es el centro de la hipérbola, los vectores tienen las direcciones de las asíntotas y es un punto de la hipérbola. El vector tangente es En un vértice la tangente es perpendicular al eje mayor. Por lo tanto y el parámetro de un vértice es
es equivalente a y son los vértices de la hipérbola.
Las siguientes propiedades de una hipérbola se demuestran fácilmente utilizando la representación de una hipérbola presentada en esta sección.
Construcción de tangente

El vector tangente se puede reescribir mediante factorización: Esto significa que
Esta propiedad proporciona una forma de construir la tangente en un punto de la hipérbola.
Esta propiedad de una hipérbola es una versión afín de la degeneración de tres puntos del teorema de Pascal . [12]
- Área del paralelogramo gris
El área del paralelogramo gris en el diagrama anterior es y, por lo tanto, independiente del punto . La última ecuación se desprende de un cálculo para el caso, donde es un vértice y la hipérbola en su forma canónica.
Construcción de puntos

Para una hipérbola con representación paramétrica (para simplificar el centro es el origen) se cumple lo siguiente:
son colineales con el centro de la hipérbola (ver diagrama).
La prueba simple es una consecuencia de la ecuación .
Esta propiedad proporciona la posibilidad de construir puntos de una hipérbola si se dan las asíntotas y un punto.
Esta propiedad de una hipérbola es una versión afín de la degeneración de 4 puntos del teorema de Pascal . [13]
Triángulo tangente-asíntota

Para simplificar, el centro de la hipérbola puede ser el origen y los vectores tienen la misma longitud. Si no se cumple el último supuesto, se puede aplicar primero una transformación de parámetros (ver arriba) para que el supuesto sea verdadero. Por lo tanto , los vértices abarcan el eje menor y se obtiene y .
Para los puntos de intersección de la tangente en el punto con las asíntotas se obtienen los puntos El área del triángulo se puede calcular mediante un determinante 2 × 2: (ver reglas para determinantes ). es el área del rombo generado por . El área de un rombo es igual a la mitad del producto de sus diagonales. Las diagonales son los semiejes de la hipérbola. Por lo tanto:
Reciprocidad de un círculo
La reciprocidad de un círculo B en un círculo C siempre produce una sección cónica como una hipérbola. El proceso de "reciprocidad en un círculo C " consiste en reemplazar cada línea y punto en una figura geométrica por su polo y polar correspondientes , respectivamente. El polo de una línea es la inversión de su punto más cercano al círculo C , mientras que el polar de un punto es el inverso, es decir, una línea cuyo punto más cercano a C es la inversión del punto.
La excentricidad de la sección cónica obtenida por reciprocidad es la relación entre las distancias entre los centros de los dos círculos y el radio r del círculo de reciprocidad C. Si B y C representan los puntos en los centros de los círculos correspondientes, entonces
Como la excentricidad de una hipérbola es siempre mayor que uno, el centro B debe estar fuera del círculo alternativo C.
Esta definición implica que la hipérbola es tanto el lugar geométrico de los polos de las rectas tangentes al círculo B como la envolvente de las rectas polares de los puntos de B. A la inversa, el círculo B es la envolvente de los polares de los puntos de la hipérbola y el lugar geométrico de los polos de las rectas tangentes a la hipérbola. Dos rectas tangentes a B no tienen polos (finitos) porque pasan por el centro C del círculo de reciprocidad C ; las polares de los puntos tangentes correspondientes de B son las asíntotas de la hipérbola. Las dos ramas de la hipérbola corresponden a las dos partes del círculo B que están separadas por estos puntos tangentes.
Ecuación cuadrática
Una hipérbola también se puede definir como una ecuación de segundo grado en las coordenadas cartesianas en el plano ,
siempre que las constantes y satisfagan la condición determinante
Este determinante se denomina convencionalmente discriminante de la sección cónica. [14]
Un caso especial de hipérbola (la hipérbola degenerada que consiste en dos líneas que se intersecan) ocurre cuando otro determinante es cero:
Este determinante a veces se denomina discriminante de la sección cónica. [15]
Los coeficientes de la ecuación general se pueden obtener a partir de las coordenadas conocidas del centro del semieje mayor y del semieje menor , y del ángulo de rotación (el ángulo desde el eje horizontal positivo hasta el eje mayor de la hipérbola) utilizando las fórmulas:
Estas expresiones pueden derivarse de la ecuación canónica
por una traslación y rotación de las coordenadas :
Dada la parametrización general anterior de la hipérbola en coordenadas cartesianas, la excentricidad se puede encontrar utilizando la fórmula en Sección cónica#Excentricidad en términos de coeficientes .
El centro de la hipérbola se puede determinar a partir de las fórmulas
En términos de nuevas coordenadas, la ecuación definitoria de la hipérbola se puede escribir
Los ejes principales de la hipérbola forman un ángulo con el eje positivo que está dado por
Al girar los ejes de coordenadas de modo que el eje esté alineado con el eje transversal, la ecuación adquiere su forma canónica.
Los semiejes mayor y menor están definidos por las ecuaciones
donde y son las raíces de la ecuación cuadrática
A modo de comparación, la ecuación correspondiente para una hipérbola degenerada (que consta de dos líneas que se cruzan) es
La línea tangente a un punto dado de la hipérbola está definida por la ecuación
donde y se definen por
La recta normal a la hipérbola en el mismo punto viene dada por la ecuación
La recta normal es perpendicular a la recta tangente y ambas pasan por el mismo punto
De la ecuación
El foco izquierdo es y el foco derecho es donde es la excentricidad. Denote las distancias desde un punto a los focos izquierdo y derecho como y Para un punto en la rama derecha,
y para un punto en la rama izquierda,
Esto se puede demostrar de la siguiente manera:
Si es un punto en la hipérbola la distancia al punto focal izquierdo es
Al punto focal derecho la distancia es
Si es un punto en la rama derecha de la hipérbola entonces y
Restando estas ecuaciones se obtiene
Si es un punto en la rama izquierda de la hipérbola entonces y
Restando estas ecuaciones se obtiene
En coordenadas cartesianas
Ecuación
Si se introducen coordenadas cartesianas de modo que el origen sea el centro de la hipérbola y el eje x sea el eje mayor, entonces la hipérbola se denomina de apertura este-oeste y
- Los focos son los puntos , [6]
- Los vértices son . [6]
Para un punto arbitrario la distancia al foco es y al segundo foco . Por lo tanto el punto está sobre la hipérbola si se cumple la siguiente condición . Eliminar las raíces cuadradas mediante elevaciones adecuadas y utilizar la relación para obtener la ecuación de la hipérbola:
Esta ecuación se llama forma canónica de una hipérbola, porque cualquier hipérbola, independientemente de su orientación relativa a los ejes cartesianos y sin importar la ubicación de su centro, puede transformarse a esta forma mediante un cambio de variables, dando una hipérbola que es congruente con la original (ver más abajo).
Los ejes de simetría o ejes principales son el eje transversal (que contiene el segmento de longitud 2 a con puntos finales en los vértices) y el eje conjugado (que contiene el segmento de longitud 2 b perpendicular al eje transversal y con punto medio en el centro de la hipérbola). [6] A diferencia de una elipse, una hipérbola tiene solo dos vértices: . Los dos puntos en los ejes conjugados no están en la hipérbola.
De la ecuación se deduce que la hipérbola es simétrica con respecto a ambos ejes de coordenadas y, por tanto, simétrica con respecto al origen.
Excentricidad
Para una hipérbola en la forma canónica anterior, la excentricidad está dada por
Dos hipérbolas son geométricamente similares entre sí, lo que significa que tienen la misma forma, de modo que una puede transformarse en la otra mediante movimientos rígidos hacia la izquierda y la derecha , rotación , toma de una imagen especular y escala (aumento), si y solo si tienen la misma excentricidad.
Asíntotas


Resolviendo la ecuación (anterior) de la hipérbola para se obtiene De esto se deduce que la hipérbola se aproxima a las dos líneas para valores grandes de . Estas dos líneas se intersecan en el centro (origen) y se denominan asíntotas de la hipérbola [16]
Con la ayuda de la segunda figura se puede ver que
- La distancia perpendicular desde un foco a cualquier asíntota es (el semieje menor).
De la forma normal de Hesse de las asíntotas y de la ecuación de la hipérbola se obtiene: [17]
- El producto de las distancias desde un punto en la hipérbola a ambas asíntotas es la constante que también puede escribirse en términos de la excentricidad e como
De la ecuación de la hipérbola (arriba) se puede derivar:
- El producto de las pendientes de las rectas desde un punto P hasta los dos vértices es la constante
Además, de (2) arriba se puede demostrar que [17]
- El producto de las distancias desde un punto en la hipérbola hasta las asíntotas a lo largo de líneas paralelas a las asíntotas es la constante
Recto semilato
La longitud de la cuerda que pasa por uno de los focos, perpendicular al eje mayor de la hipérbola, se llama lado recto . La mitad de esta es el semilato recto . Un cálculo muestra que el semilato recto también puede considerarse como el radio de curvatura en los vértices.
Tangente
La forma más sencilla de determinar la ecuación de la tangente en un punto es derivar implícitamente la ecuación de la hipérbola. Denotando dy/dx como y′ , esto produce Con respecto a , la ecuación de la tangente en el punto es
Una línea tangente particular distingue la hipérbola de las otras secciones cónicas. [18] Sea f la distancia desde el vértice V (tanto en la hipérbola como en su eje a través de los dos focos) hasta el foco más cercano. Entonces, la distancia, a lo largo de una línea perpendicular a ese eje, desde ese foco hasta un punto P en la hipérbola es mayor que 2 f . La tangente a la hipérbola en P interseca ese eje en el punto Q en un ángulo ∠PQV mayor que 45°.
Hipérbola rectangular
En el caso de la hipérbola se denomina rectangular (o equilátera ), porque sus asíntotas se cortan en ángulos rectos. Para este caso, la excentricidad lineal es , la excentricidad y el semilato recto . La gráfica de la ecuación es una hipérbola rectangular.
Representación paramétrica con seno/coseno hiperbólico
Utilizando las funciones seno y coseno hiperbólicos , se puede obtener una representación paramétrica de la hipérbola , que es similar a la representación paramétrica de una elipse: que satisface la ecuación cartesiana porque
En la sección Ecuaciones paramétricas a continuación se dan representaciones paramétricas adicionales.

Hipérbola conjugada
Intercambiamos y obtenemos la ecuación de la hipérbola conjugada (ver diagrama): también escrita como
Una hipérbola y su conjugada pueden tener diámetros que son conjugados . En la teoría de la relatividad especial , dichos diámetros pueden representar ejes de tiempo y espacio, donde una hipérbola representa eventos a una distancia espacial dada del centro , y la otra representa eventos a una distancia temporal correspondiente del centro.
En coordenadas polares



Origen en el foco
Las coordenadas polares utilizadas más comúnmente para la hipérbola se definen en relación con el sistema de coordenadas cartesianas que tiene su origen en un foco y su eje x apunta hacia el origen del "sistema de coordenadas canónicas", como se ilustra en el primer diagrama.
En este caso el ángulo se llama anomalía verdadera .
En relación a este sistema de coordenadas se tiene que
y
Origen en el centro
Con coordenadas polares relativas al "sistema de coordenadas canónicas" (ver segundo diagrama) se tiene que
Para la rama derecha de la hipérbola el rango de es
Excentricidad
Cuando se utilizan coordenadas polares, la excentricidad de la hipérbola se puede expresar como donde es el límite de la coordenada angular. A medida que se acerca a este límite, r se acerca al infinito y el denominador en cualquiera de las ecuaciones mencionadas anteriormente se acerca a cero, por lo tanto: [19] : 219
Ecuaciones paramétricas
Una hipérbola con ecuación se puede describir mediante varias ecuaciones paramétricas:
- A través de funciones trigonométricas hiperbólicas
- Como representación racional
- A través de funciones trigonométricas circulares
- Con la pendiente tangente como parámetro:Una representación paramétrica, que utiliza la pendiente de la tangente en un punto de la hipérbola, se puede obtener de forma análoga al caso de la elipse: Sustituir en el caso de la elipse por y utilizar fórmulas para las funciones hiperbólicas . Se obtiene aquí, es la mitad superior y la mitad inferior de la hipérbola. Los puntos con tangentes verticales (vértices ) no están cubiertos por la representación.La ecuación de la tangente en el punto es Esta descripción de las tangentes de una hipérbola es una herramienta esencial para la determinación de la ortóptica de una hipérbola.
Funciones hiperbólicas

Así como las funciones trigonométricas se definen en términos del círculo unitario , también las funciones hiperbólicas se definen en términos de la hipérbola unitaria , como se muestra en este diagrama. En un círculo unitario, el ángulo (en radianes) es igual al doble del área del sector circular que subtiende ese ángulo. El ángulo hiperbólico análogo se define asimismo como el doble del área de un sector hiperbólico .
Sea el doble del área entre el eje y un rayo que pasa por el origen e interseca la hipérbola unitaria, y definamos como las coordenadas del punto de intersección. Entonces el área del sector hiperbólico es el área del triángulo menos la región curvada más allá del vértice en : que se simplifica al área del coseno hiperbólico. Resolviendo para se obtiene la forma exponencial del coseno hiperbólico: De uno se obtiene y su inversa el área del seno hiperbólico : Otras funciones hiperbólicas se definen de acuerdo con el coseno hiperbólico y el seno hiperbólico, así por ejemplo
Propiedades
Propiedad de reflexión

La tangente en un punto biseca el ángulo entre las líneas. Esto se llama propiedad óptica o propiedad de reflexión de una hipérbola. [20]
- Prueba
Sea el punto de la recta que se encuentra a la distancia del foco (ver diagrama, es el semieje mayor de la hipérbola). La recta es la bisectriz del ángulo que forman las rectas . Para demostrar que es la recta tangente en el punto , se comprueba que cualquier punto de la recta que sea distinto de no puede estar en la hipérbola. Por lo tanto, solo tiene un punto en común con la hipérbola y es, por tanto, la tangente en el punto .
Del diagrama y de la desigualdad del triángulo se reconoce que se cumple, lo que significa: . Pero si es un punto de la hipérbola, la diferencia debería ser .
Puntos medios de cuerdas paralelas


Los puntos medios de las cuerdas paralelas de una hipérbola se encuentran en una línea que pasa por el centro (ver diagrama).
Los puntos de cualquier cuerda pueden estar en diferentes ramas de la hipérbola.
La prueba de la propiedad sobre los puntos medios se realiza mejor para la hipérbola . Debido a que cualquier hipérbola es una imagen afín de la hipérbola (ver la sección a continuación) y una transformación afín preserva el paralelismo y los puntos medios de los segmentos de línea, la propiedad es verdadera para todas las hipérbolas:
Para dos puntos de la hipérbola
- El punto medio de la cuerda es
- La pendiente de la cuerda es
Para cuerdas paralelas, la pendiente es constante y los puntos medios de las cuerdas paralelas se encuentran en la línea.
Consecuencia: para cualquier par de puntos de una cuerda existe una reflexión oblicua con un eje (conjunto de puntos fijos) que pasa por el centro de la hipérbola, que intercambia los puntos y deja fija la hipérbola (en su conjunto). Una reflexión oblicua es una generalización de una reflexión ordinaria a través de una línea , donde todos los pares de puntos-imagen están sobre una línea perpendicular a .
Como una reflexión oblicua deja fija la hipérbola, el par de asíntotas también queda fijo. Por lo tanto, el punto medio de una cuerda divide también en mitades el segmento de línea relacionado entre las asíntotas. Esto significa que . Esta propiedad se puede utilizar para la construcción de otros puntos de la hipérbola si se dan un punto y las asíntotas.
Si la cuerda degenera en una tangente , entonces el punto de contacto divide el segmento de línea entre las asíntotas en dos mitades.
Tangentes ortogonales – ortóptica

En una hipérbola, los puntos de intersección de las tangentes ortogonales se encuentran en el círculo .
Este círculo se denomina ortóptica de la hipérbola dada.
Las tangentes pueden pertenecer a puntos de diferentes ramas de la hipérbola.
En caso de que no existan pares de tangentes ortogonales.
Relación polo-polar para una hipérbola

Cualquier hipérbola se puede describir en un sistema de coordenadas adecuado mediante una ecuación . La ecuación de la tangente en un punto de la hipérbola es Si se permite que el punto sea un punto arbitrario diferente del origen, entonces
- El punto se asigna a la línea , no a través del centro de la hipérbola.
Esta relación entre puntos y líneas es una biyección .
Los mapas de funciones inversas
- línea sobre el punto y
- línea sobre el punto
Esta relación entre puntos y líneas generada por una cónica se denomina relación polo-polar o simplemente polaridad . El polo es el punto, el polar la línea. Véase Polo y polar .
Mediante el cálculo se comprueban las siguientes propiedades de la relación polo-polar de la hipérbola:
- Para un punto (polo) de la hipérbola, la polar es la tangente en ese punto (ver diagrama: ).
- Para un polo fuera de la hipérbola los puntos de intersección de su polar con la hipérbola son los puntos de tangencia de las dos tangentes que pasan (ver diagrama: ).
- Para un punto dentro de la hipérbola, la polar no tiene ningún punto en común con la hipérbola. (ver diagrama: ).
Observaciones:
- El punto de intersección de dos polares (por ejemplo: ) es el polo de la línea que pasa por sus polos (aquí: ).
- Los focos y respectivamente y las directrices y respectivamente pertenecen a pares de polo y polar.
También existen relaciones polo-polares para elipses y parábolas.
Otras propiedades
- Son concurrentes : (1) un círculo que pasa por los focos de la hipérbola y tiene como centro el centro de la hipérbola; (2) cualquiera de las líneas que son tangentes a la hipérbola en los vértices; y (3) cualquiera de las asíntotas de la hipérbola. [21] [22]
- También son concurrentes: (1) el círculo que tiene su centro en el centro de la hipérbola y que pasa por los vértices de la hipérbola; (2) cualquiera de las directriz; y (3) cualquiera de las asíntotas. [22]
- Dado que tanto el eje transversal como el eje conjugado son ejes de simetría, el grupo de simetría de una hipérbola es el cuatrigrupo de Klein .
- Las hipérbolas rectangulares xy = constante admiten acciones de grupo por aplicaciones de compresión que tienen las hipérbolas como conjuntos invariantes .
Longitud del arco
La longitud de arco de una hipérbola no tiene una expresión elemental . La mitad superior de una hipérbola se puede parametrizar como
Entonces la integral que da la longitud del arco desde hasta se puede calcular como:
Después de utilizar la sustitución , esto también se puede representar utilizando la integral elíptica incompleta de segundo tipo con parámetro :
Usando sólo números reales, esto se convierte en [23]
donde es la integral elíptica incompleta de primer tipo con parámetro y es la función Gudermanniana .
Curvas derivadas

A partir de la hipérbola por inversión se pueden derivar otras curvas , las llamadas curvas inversas de la hipérbola. Si se elige el centro de inversión como el propio centro de la hipérbola, la curva inversa es la lemniscata de Bernoulli ; la lemniscata es también la envolvente de círculos centrados en una hipérbola rectangular y que pasan por el origen. Si se elige el centro de inversión en un foco o en un vértice de la hipérbola, las curvas inversas resultantes son un limazón o una estrofoide , respectivamente.
Coordenadas elípticas
Una familia de hipérbolas confocales es la base del sistema de coordenadas elípticas en dos dimensiones. Estas hipérbolas se describen mediante la ecuación
donde los focos se encuentran a una distancia c del origen en el eje x , y donde θ es el ángulo de las asíntotas con el eje x . Toda hipérbola de esta familia es ortogonal a toda elipse que comparte los mismos focos. Esta ortogonalidad puede demostrarse mediante un mapa conforme del sistema de coordenadas cartesianas w = z + 1/ z , donde z = x + iy son las coordenadas cartesianas originales, y w = u + iv son las posteriores a la transformación.
Se pueden obtener otros sistemas de coordenadas bidimensionales ortogonales que incluyan hipérbolas mediante otras aplicaciones conformes. Por ejemplo, la aplicación w = z 2 transforma el sistema de coordenadas cartesianas en dos familias de hipérbolas ortogonales.
Análisis de la sección cónica de la apariencia hiperbólica de los círculos

Como imágenes de los círculos se obtienen un círculo (magenta), elipses, hipérbolas y líneas. El caso especial de una parábola no aparece en este ejemplo.
(Si el centro O estuviera sobre la esfera, todas las imágenes de los círculos serían círculos o líneas; véase proyección estereográfica ).
Además de proporcionar una descripción uniforme de círculos, elipses, parábolas e hipérbolas, las secciones cónicas también pueden entenderse como un modelo natural de la geometría de la perspectiva en el caso en que la escena que se observa consiste en círculos o, de manera más general, una elipse. El espectador es típicamente una cámara o el ojo humano y la imagen de la escena es una proyección central sobre un plano de imagen, es decir, todos los rayos de proyección pasan por un punto fijo O , el centro. El plano de la lente es un plano paralelo al plano de la imagen en la lente O .
La imagen de un círculo c es
- un círculo , si el círculo c está en una posición especial, por ejemplo paralelo al plano de la imagen y otros (ver proyección estereográfica),
- una elipse , si c no tiene ningún punto en común con el plano de la lente,
- una parábola , si c tiene un punto con el plano de la lente en común y
- una hipérbola , si c tiene dos puntos con el plano de la lente en común.
(Se omiten las posiciones especiales donde el plano del círculo contiene el punto O ).
Estos resultados se pueden entender si se reconoce que el proceso de proyección se puede ver en dos pasos: 1) el círculo c y el punto O generan un cono que es 2) cortado por el plano de la imagen, para generar la imagen.
Se ve una hipérbola cuando se ve una porción de un círculo cortado por el plano de la lente. La incapacidad de ver gran parte de los brazos de la rama visible, combinada con la ausencia total de la segunda rama, hace que sea prácticamente imposible para el sistema visual humano reconocer la conexión con las hipérbolas.
Aplicaciones


Relojes de sol
Las hipérbolas se pueden ver en muchos relojes de sol . En un día cualquiera, el sol gira en un círculo sobre la esfera celeste y sus rayos que inciden en el punto de un reloj de sol trazan un cono de luz. La intersección de este cono con el plano horizontal del suelo forma una sección cónica. En las latitudes más pobladas y en la mayoría de las épocas del año, esta sección cónica es una hipérbola. En términos prácticos, la sombra de la punta de un poste traza una hipérbola en el suelo a lo largo de un día (esta trayectoria se llama línea de declinación ). La forma de esta hipérbola varía con la latitud geográfica y con la época del año, ya que esos factores afectan al cono de los rayos del sol en relación con el horizonte. La colección de tales hipérbolas durante un año entero en un lugar determinado se llamaba pelekinon por los griegos, ya que se asemeja a un hacha de doble filo.
Multilateración
La hipérbola es la base para resolver problemas de multilateración , es decir, la tarea de localizar un punto a partir de las diferencias en sus distancias a puntos dados o, equivalentemente, la diferencia en los tiempos de llegada de señales sincronizadas entre el punto y los puntos dados. Estos problemas son importantes en la navegación, particularmente en el agua; un barco puede localizar su posición a partir de la diferencia en los tiempos de llegada de las señales de un transmisor LORAN o GPS . A la inversa, una baliza de localización o cualquier transmisor puede localizarse comparando los tiempos de llegada de sus señales a dos estaciones receptoras separadas; estas técnicas pueden utilizarse para rastrear objetos y personas. En particular, el conjunto de posibles posiciones de un punto que tiene una diferencia de distancia de 2 a desde dos puntos dados es una hipérbola con una separación de vértices de 2 a cuyos focos son los dos puntos dados.
Trayectoria seguida por una partícula
La trayectoria seguida por cualquier partícula en el problema clásico de Kepler es una sección cónica . En particular, si la energía total E de la partícula es mayor que cero (es decir, si la partícula no está ligada), la trayectoria de dicha partícula es una hipérbola. Esta propiedad es útil para estudiar las fuerzas atómicas y subatómicas mediante la dispersión de partículas de alta energía; por ejemplo, el experimento de Rutherford demostró la existencia de un núcleo atómico al examinar la dispersión de partículas alfa de átomos de oro . Si se ignoran las interacciones nucleares de corto alcance, el núcleo atómico y la partícula alfa interactúan solo mediante una fuerza de Coulomb repulsiva , que satisface el requisito de la ley del cuadrado inverso para un problema de Kepler. [24]
Ecuación de Korteweg-de Vries
La función trigonométrica hiperbólica aparece como una solución a la ecuación de Korteweg-de Vries que describe el movimiento de una onda solitón en un canal.
Trisección de ángulos

Como lo demostró por primera vez Apolonio de Perge , una hipérbola puede usarse para trisecar cualquier ángulo , un problema de geometría bien estudiado. Dado un ángulo, primero dibuje un círculo centrado en su vértice O , que interseca los lados del ángulo en los puntos A y B. A continuación, dibuje el segmento de línea con los puntos finales A y B y su bisectriz perpendicular . Construya una hipérbola de excentricidad e = 2 con como directriz y B como foco. Sea P la intersección (superior) de la hipérbola con el círculo. El ángulo POB triseca el ángulo AOB .
Para demostrarlo, se refleja el segmento OP respecto de la recta que obtiene el punto P' como imagen de P . El segmento AP' tiene la misma longitud que el segmento BP debido a la reflexión, mientras que el segmento PP' tiene la misma longitud que el segmento BP debido a la excentricidad de la hipérbola. [25] Como OA , OP' , OP y OB son todos radios del mismo círculo (y por tanto, tienen la misma longitud), los triángulos OAP' , OPP' y OPB son todos congruentes. Por lo tanto, el ángulo ha sido trisecado, ya que 3× POB = AOB . [26]
Frontera de cartera eficiente
En la teoría de carteras , el lugar geométrico de las carteras eficientes en términos de media-varianza (llamado frontera eficiente) es la mitad superior de la rama que abre hacia el este de una hipérbola dibujada con la desviación estándar del rendimiento de la cartera graficada horizontalmente y su valor esperado graficado verticalmente; según esta teoría, todos los inversores racionales elegirían una cartera caracterizada por algún punto en este lugar geométrico.
Bioquímica
En bioquímica y farmacología , la ecuación de Hill y la ecuación de Hill-Langmuir describen respectivamente las respuestas biológicas y la formación de complejos proteína-ligando en función de la concentración de ligando. Ambas son hipérbolas rectangulares.
Hipérbolas como secciones planas de cuádricas
Las hipérbolas aparecen como secciones planas de las siguientes cuádricas :
- Cono elíptico
- Cilindro hiperbólico
- Paraboloide hiperbólico
- Hiperboloide de una lámina
- Hiperboloide de dos láminas
- Cono elíptico
- Cilindro hiperbólico
- Paraboloide hiperbólico
- Hiperboloide de una lámina
- Hiperboloide de dos láminas
Véase también
Otras secciones cónicas
Otros temas relacionados
- Coordenadas elípticas , un sistema de coordenadas ortogonales basado en familias de elipses e hipérbolas.
- Crecimiento hiperbólico
- Ecuación diferencial parcial hiperbólica
- Sector hiperbólico
- Estructura hiperboloide
- Trayectoria hiperbólica
- Hiperboloide
- Multilateración
- Rotación de ejes
- Traducción de ejes
- Hipérbola unitaria
Notas
- ^ desde Oakley 1944, pág. 17.
- ^ Heath, Sir Thomas Little (1896), "Capítulo I. El descubrimiento de las secciones cónicas. Menecmo", Apolonio de Perga: Tratado sobre las secciones cónicas con introducciones que incluyen un ensayo sobre la historia anterior del tema, Cambridge University Press, pp. xvii–xxx.
- ^ Boyer, Carl B.; Merzbach, Uta C. (2011), Una historia de las matemáticas, Wiley, pág. 73, ISBN 9780470630563Fue Apolonio
(posiblemente siguiendo una sugerencia de Arquímedes) quien introdujo los nombres "elipse" e "hipérbola" en relación con estas curvas.
- ^ Eves, Howard (1963), Un estudio de la geometría (vol. uno) , Allyn y Bacon, págs. 30-31
- ^ Protter y Morrey 1970, págs. 308–310.
- ^ abcd Protter y Morrey 1970, pag. 310.
- ^ Apóstol, Tom M.; Mnatsakanian, Mamikon A. (2012), Nuevos horizontes en geometría , The Dolciani Mathematical Expositions #47, The Mathematical Association of America, p. 251, ISBN 978-0-88385-354-2
- ^ El término alemán para este círculo es Leitkreis , que puede traducirse como "círculo de directores", pero ese término tiene un significado diferente en la literatura inglesa (ver Círculo de directores ).
- ^ Frans van Schooten : Mathematische Oeffeningen , Leyden, 1659, p. 327
- ^ E. Hartmann: Nota de clase 'Geometrías de círculos planos', Introducción a los planos de Möbius, Laguerre y Minkowski, pág. 93
- ^ W. Benz: Vorlesungen über Geomerie der Algebren , Springer (1973)
- ^ Nota de clase Geometrías de círculos planos, Introducción a los planos de Moebius, Laguerre y Minkowski, pág. 33, (PDF; 757 kB)
- ^ Nota de clase Geometrías de círculos planos, Introducción a los planos de Moebius, Laguerre y Minkowski, pág. 32 (PDF; 757 kB)
- ^ Fanchi, John R. (2006). Actualización de matemáticas para científicos e ingenieros. John Wiley and Sons. Sección 3.2, páginas 44-45. ISBN 0-471-75715-2.
- ^ Korn, Granino A; Korn, Theresa M. (2000). Manual matemático para científicos e ingenieros: definiciones, teoremas y fórmulas para referencia y revisión (segunda edición). Dover Publ. pág. 40.
- ^ Protter y Morrey 1970, págs. APP-29 – APP-30.
- ^ ab Mitchell, Douglas W., "Una propiedad de las hipérbolas y sus asíntotas", Mathematical Gazette 96, julio de 2012, 299–301.
- ^ JW Downs, Secciones cónicas prácticas , Dover Publ., 2003 (orig. 1993): pág. 26.
- ^ Casey, John, (1885) "Un tratado sobre la geometría analítica de las secciones puntuales, lineales, circulares y cónicas, que contiene un relato de sus extensiones más recientes, con numerosos ejemplos"
- ^ Coffman, RT; Ogilvy, CS (1963), "La 'propiedad de reflexión' de las cónicas", Mathematics Magazine , 36 (1): 11–12, doi :10.2307/2688124 Flanders, Harley (1968), "La propiedad óptica de las cónicas", American Mathematical Monthly , 75 (4): 399, doi :10.2307/2313439
Brozinsky, Michael K. (1984), "Propiedad de reflexión de la elipse y la hipérbola", College Mathematics Journal , 15 (2): 140–42, doi :10.2307/2686519
- ^ "Hipérbola". Mathafou.free.fr . Archivado desde el original el 4 de marzo de 2016. Consultado el 26 de agosto de 2018 .
- ^ ab "Propiedades de una hipérbola". Archivado desde el original el 2 de febrero de 2017. Consultado el 22 de junio de 2011 .
- ^ Carlson, BC (2010), "Integrales elípticas", en Olver, Frank WJ ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), Manual del NIST de funciones matemáticas , Cambridge University Press, ISBN 978-0-521-19225-5, Sr. 2723248.
- ^ Heilbron, John L. (1968). "La dispersión de partículas α y β y el átomo de Rutherford". Archivo de Historia de las Ciencias Exactas . 4 (4): 247–307. doi :10.1007/BF00411591. ISSN 0003-9519. JSTOR 41133273.
- ^ Dado que 2 veces la distancia de P a es PP' que es igual a BP por la propiedad directriz-foco
- ^ Esta construcción se debe a Pappus de Alejandría (circa 300 d.C.) y la prueba proviene de Kazarinoff 1970, p. 62.
Referencias
- Kazarinoff, Nicholas D. (1970), Regla y círculo, Boston: Prindle, Weber & Schmidt, ISBN 0-87150-113-9
- Oakley, CO, Ph.D. (1944), Un esquema del cálculo , Nueva York: Barnes & Noble
{{citation}}: CS1 maint: multiple names: authors list (link) - Protter, Murray H. ; Morrey, Charles B. Jr. (1970), Cálculo universitario con geometría analítica (2.ª ed.), Reading: Addison-Wesley , LCCN 76087042
Enlaces externos
- "Hipérbola", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
- Derivación de la hipérbola en la convergencia según Apolonio
- Frans van Schooten: Mathematische Oeffeningen, 1659
- Weisstein, Eric W. "Hipérbola". MathWorld .



























































































































































![{\displaystyle t_{0}=\pm {\sqrt[{4}]{\frac {{\vec {f}}_{2}^{2}}{{\vec {f}}_{1} ^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b26de698fecd55664d5a6833e97148678656143)







































![{\displaystyle {\begin{aligned}A_{xx}&=-a^{2}\sin ^{2}\theta +b^{2}\cos ^{2}\theta ,&B_{x}&=-A_{xx}x_{\circ }-A_{xy}y_{\circ },\\[1ex]A_{yy}&=-a^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta ,&B_{y}&=-A_{xy}x_{\circ }-A_{yy}y_{\circ },\\[1ex]A_{xy}&=\left(a^{2}+b^{2}\right)\sin \theta \cos \theta ,&C&=A_{xx}x_{\circ }^{2}+2A_{xy}x_{\circ }y_{\circ }+A_{yy}y_{\circ }^{2}-a^{2}b^{2}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d82bf36f4898cad69a72588b95496e07d87d0b)



![{\displaystyle {\begin{vmatrix}B_{x}&A_{xy}\\B_{y}&A_{yy}\end{vmatrix}}\,,\\[1ex]y_{c}&=-{\frac {1}{D}}\,{\begin{vmatrix}A_{xx}&B_{x}\\A_{xy}&B_{y}\end{vmatrix}}\,.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad1cc8fb27ca4ad3d69e8490a1892b0ab44e7807)








![{\displaystyle {\begin{aligned}a^{2}&=-{\frac {\Delta }{\lambda _{1}D}}=-{\frac {\Delta }{\lambda _{1}^{2}\lambda _{2}}},\\[1ex]b^{2}&=-{\frac {\Delta }{\lambda _{2}D}}=-{\frac {\Delta }{\lambda _{1}\lambda _{2}^{2}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d190f3114f60766f993e1a4c00daaf99510f81e)









![{\displaystyle {\begin{aligned}E&=A_{xx}x_{0}+A_{xy}y_{0}+B_{x},\\[1ex]F&=A_{xy}x_{0}+A_{yy}y_{0}+B_{y},\\[1ex]G&=B_{x}x_{0}+B_{y}y_{0}+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/467ab27ea151bfad56ade7e716548b668119769c)





































































![{\displaystyle {\begin{cases}x=\pm a{\dfrac {t^{2}+1}{2t}},\\[1ex]y=b{\dfrac {t^{2}-1}{2t}},\end{cases}}\qquad t>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4638f9752638e31c275c9603c3a41d4dc43c45b6)














![{\displaystyle {\begin{aligned}{\frac {a}{2}}&={\frac {xy}{2}}-\int _{1}^{x}{\sqrt {t^{2}-1}}\,dt\\[1ex]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-1}}\right)-{\frac {1}{2}}\left(x{\sqrt {x^{2}-1}}-\ln \left(x+{\sqrt {x^{2}-1}}\right)\right),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/613cf8b1eff7b14395982b578e9a46790fd7b3fd)
















































![{\displaystyle s=ib{\Biggr [}E\left(iv\,{\Biggr |}\,1+{\frac {a^{2}}{b^{2}}}\right){\Biggr ]}_{\operatorname {arcosh} {\frac {x_{2}}{a}}}^{\operatorname {arcosh} {\frac {x_{1}}{a}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f5d0c6796e5b98e06e3a1823868ff218bade95d)
![{\displaystyle s=b\left[F\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)-E\left(\operatorname {gd} v\,{\Biggr |}-{\frac {a^{2}}{b^{2}}}\right)+{\sqrt {1+{\frac {a^{2}}{b^{2}}}\tanh ^{2}v}}\,\sinh v\right]_{\operatorname {arcosh} {\tfrac {x_{1}}{a}}}^{\operatorname {arcosh} {\tfrac {x_{2}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11d1ab93c8a700748cb97ea55602b710787b1250)










