Limazón

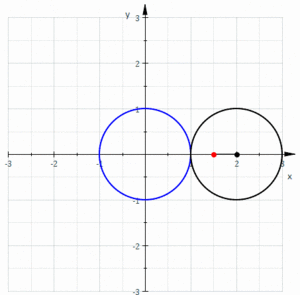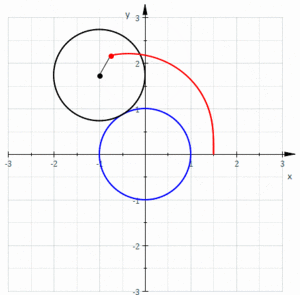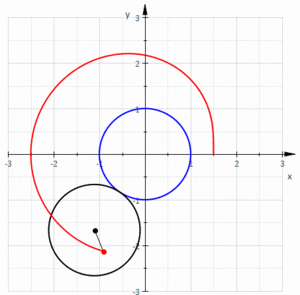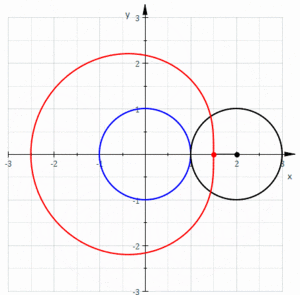
En geometría , un limaçon o limacon / ˈlɪməsɒn / , también conocido como limaçon de Pascal o caracol de Pascal , se define como una curva de ruleta formada por la trayectoria de un punto fijado a un círculo cuando dicho círculo rueda alrededor del exterior de un círculo de igual radio. También se puede definir como la ruleta formada cuando un círculo rueda alrededor de un círculo con la mitad de su radio de modo que el círculo menor quede dentro del círculo mayor. Así, pertenecen a la familia de curvas llamadas trocoides centradas ; más concretamente, son epitrocoides . La cardioide es el caso especial en el que el punto generador de la ruleta se encuentra sobre el círculo rodante; la curva resultante tiene una cúspide .

Dependiendo de la posición del punto que genera la curva, esta puede tener bucles internos y externos (que dan el nombre a la familia), puede tener forma de corazón o puede ser ovalada.

Un limazón es una curva algebraica plana racional bicircular de grado 4.

Las primeras investigaciones formales sobre los limaçons se atribuyen generalmente a Étienne Pascal , padre de Blaise Pascal . Sin embargo, algunas investigaciones esclarecedoras sobre ellos ya habían sido realizadas antes por el artista renacentista alemán Alberto Durero . La Underweysung der Messung (Instrucción sobre la medición) de Durero contiene métodos geométricos específicos para producir limaçons. La curva fue nombrada por Gilles de Roberval cuando la utilizó como ejemplo para encontrar líneas tangentes.

La ecuación (hasta la traslación y rotación) de un limaçon en coordenadas polares tiene la forma

${\displaystyle r=b+a\cos \theta .}$

Esto se puede convertir a coordenadas cartesianas multiplicando por r (introduciendo así un punto en el origen que en algunos casos es espurio) y sustituyendo y para obtener ^[1].${\displaystyle r^{2}=x^{2}+y^{2}}$${\displaystyle r\cos \theta =x}$

${\displaystyle \left(x^{2}+y^{2}-ax\right)^{2}=b^{2}\left(x^{2}+y^{2}\right).}$

Aplicando la forma paramétrica de la conversión polar a cartesiana, también tenemos ^[2]

${\displaystyle x=(b+a\cos \theta )\cos \theta ={a \over 2}+b\cos \theta +{a \over 2}\cos 2\theta ,}$

${\displaystyle y=(b+a\cos \theta )\sin \theta =b\sin \theta +{a \over 2}\sin 2\theta ;}$

mientras se establece

${\displaystyle z=x+iy=(b+a\cos \theta )(\cos \theta +i\sin \theta )}$

produce esta parametrización como una curva en el plano complejo :

${\displaystyle z={a \over 2}+be^{i\theta }+{a \over 2}e^{2i\theta }.}$

Si nos desplazáramos horizontalmente por , es decir,${\textstyle -{\frac {1}{2}}a}$

${\displaystyle z=be^{it}+{a \over 2}e^{2it}}$,

Cambiaríamos la posición del origen para convertir la ecuación de un trocoide centrado a la forma habitual. Observe el cambio de variable independiente en este punto para dejar en claro que ya no estamos utilizando la parametrización de coordenadas polares predeterminada .${\displaystyle \theta =\arg z}$

En el caso especial , la ecuación polar es${\displaystyle a=b}$

${\displaystyle r=b(1+\cos \theta )=2b\cos ^{2}{\frac {\theta }{2}}}$

o

${\displaystyle r^{1 \over 2}=(2b)^{1 \over 2}\cos {\frac {\theta }{2}},}$

lo que la convierte en miembro de la familia de curvas espirales sinusoidales . Esta curva es la cardioide .

En el caso especial , la forma trocoide centrada de la ecuación se convierte en${\displaystyle a=2b}$

${\displaystyle z=b\left(e^{it}+e^{2it}\right)=be^{3it \over 2}\left(e^{it \over 2}+e^{-it \over 2}\right)=2be^{3it \over 2}\cos {t \over 2},}$

o, en coordenadas polares,

${\displaystyle r=2b\cos {\theta \over 3}}$

Por lo que es un miembro de la familia de curvas de las rosas . Esta curva es una trisectriz y a veces se la llama trisectriz de limaçon .

Cuando , el limazón es una curva cerrada simple. Sin embargo, el origen satisface la ecuación cartesiana dada anteriormente, por lo que la gráfica de esta ecuación tiene un nodo o punto aislado.${\displaystyle b>a}$

Cuando , el área limitada por la curva es convexa, y cuando , la curva tiene una sangría limitada por dos puntos de inflexión . En , el punto es un punto de curvatura 0 .${\displaystyle b>2a}$${\displaystyle a<b<2a}$${\displaystyle b=2a}$${\displaystyle (-a,0)}$

A medida que disminuye con respecto a , la sangría se hace más pronunciada hasta que, en , la curva se vuelve cardioide y la sangría se convierte en una cúspide . Para , la cúspide se expande hasta convertirse en un bucle interno y la curva se cruza a sí misma en el origen. A medida que se acerca a 0, el bucle llena la curva externa y, en el límite, el limaçon se convierte en un círculo atravesado dos veces.${\displaystyle b}$${\displaystyle a}$${\displaystyle b=a}$${\displaystyle 0<b<a}$${\displaystyle b}$

El área encerrada por el limazón es . Cuando esto cuenta el área encerrada por el bucle interior dos veces. En este caso, la curva cruza el origen en ángulos , el área encerrada por el bucle interior es${\displaystyle r=b+a\cos \theta }$${\textstyle \left(b^{2}+{{a^{2}} \over 2}\right)\pi }$${\displaystyle b<a}$${\textstyle \pi \pm \arccos {b \over a}}$

${\displaystyle \left(b^{2}+{{a^{2}} \over 2}\right)\arccos {b \over a}-{3 \over 2}b{\sqrt {a^{2}-b^{2}}},}$

El área encerrada por el bucle exterior es

${\displaystyle \left(b^{2}+{{a^{2}} \over 2}\right)\left(\pi -\arccos {b \over a}\right)+{3 \over 2}b{\sqrt {a^{2}-b^{2}}},}$

y el área entre los bucles es

${\displaystyle \left(b^{2}+{{a^{2}} \over 2}\right)\left(\pi -2\arccos {b \over a}\right)+3b{\sqrt {a^{2}-b^{2}}}.}$^[1]

La circunferencia del limazón está dada por una integral elíptica completa de segundo tipo :

${\displaystyle 4(a+b)E\left({{2{\sqrt {ab}}} \over a+b}\right).}$

• Sea un punto y un círculo cuyo centro no es . Entonces la envolvente de esos círculos cuyo centro está en y que pasan por él es un limazón.${\displaystyle P}$${\displaystyle C}$${\displaystyle P}$${\displaystyle C}$${\displaystyle P}$

• Un pedal de un círculo es un limaçon. De hecho, el pedal con respecto al origen del círculo con radio y centro tiene ecuación polar .${\displaystyle b}$${\displaystyle (a,0)}$${\displaystyle r=b+a\cos \theta }$

• La inversa con respecto al círculo unitario de es${\displaystyle r=b+a\cos \theta }$

${\displaystyle r={1 \over {b+a\cos \theta }}}$

que es la ecuación de una sección cónica con excentricidad y foco en el origen. Por lo tanto, un limazón se puede definir como la inversa de una cónica donde el centro de inversión es uno de los focos. Si la cónica es una parábola, entonces la inversa será un cardioide, si la cónica es una hipérbola, entonces el limazón correspondiente tendrá un bucle interior, y si la cónica es una elipse, entonces el limazón correspondiente no tendrá bucle.${\displaystyle {\tfrac {a}{b}}}$

• La concoide de un círculo con respecto a un punto del círculo es un limazón.

• Un caso particular de óvalo cartesiano es el limazón. ^[3]

• Ruleta
• Trocoide centrado
• Lista de funciones periódicas

• Jane Grossman y Michael Grossman. "Con hoyuelos o sin hoyuelos", The Two-Year College Mathematics Journal , enero de 1982, páginas 52-55.
• Howard Anton. Cálculo , 2.ª edición, página 708, John Wiley & Sons, 1984.
• Howard Anton. [1] págs. 725 – 726.
• Howard Eves. Un estudio de la geometría , volumen 2 (páginas 51, 56, 273), Allyn y Bacon, 1965.

Wikimedia Commons alberga una categoría multimedia sobre Limacon .

• Limacon de Pascal en The MacTutor Historia de las Matemáticas
• Limaçon en Curvas matemáticas
• Limaçon de Pascal en ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES
• Limacon de Pascal en el Diccionario visual de curvas planas especiales
• "Limacón de Pascal" en PlanetPTC (Mathcad)