Curva algebraica
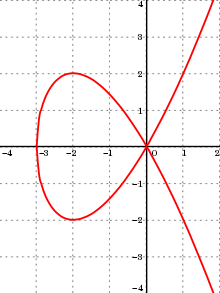
Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . ( agosto de 2023 ) |
En matemáticas , una curva plana algebraica afín es el conjunto cero de un polinomio en dos variables. Una curva plana algebraica proyectiva es el conjunto cero en un plano proyectivo de un polinomio homogéneo en tres variables. Una curva plana algebraica afín se puede completar en una curva plana algebraica proyectiva homogeneizando su polinomio definitorio. Por el contrario, una curva plana algebraica proyectiva de ecuación homogénea h ( x , y , t ) = 0 se puede restringir a la curva plana algebraica afín de ecuación h ( x , y , 1) = 0 . Estas dos operaciones son cada una inversa a la otra; por lo tanto, la frase curva plana algebraica se utiliza a menudo sin especificar explícitamente si se considera el caso afín o el proyectivo.
Si el polinomio que define una curva algebraica plana es irreducible , entonces se tiene una curva algebraica plana irreducible . En caso contrario, la curva algebraica es la unión de una o varias curvas irreducibles, llamadas sus componentes , que están definidas por los factores irreducibles.
En términos más generales, una curva algebraica es una variedad algebraica de dimensión uno. (En algunos contextos, un conjunto algebraico de dimensión uno también se denomina curva algebraica, pero este no será el caso en este artículo). De manera equivalente, una curva algebraica es una variedad algebraica que es biracionalmente equivalente a una curva plana algebraica irreducible. Si la curva está contenida en un espacio afín o un espacio proyectivo , se puede tomar una proyección para tal equivalencia biracional.
Estas equivalencias biracionales reducen la mayor parte del estudio de las curvas algebraicas al estudio de las curvas planas algebraicas. Sin embargo, algunas propiedades no se mantienen bajo la equivalencia biracional y deben estudiarse en curvas no planas. Este es, en particular, el caso del grado y la suavidad . Por ejemplo, existen curvas suaves de género 0 y grado mayor que dos, pero cualquier proyección plana de tales curvas tiene puntos singulares (véase la fórmula de género-grado ).
Una curva no plana a menudo se denomina curva espacial o curva oblicua .
En geometría euclidiana
Una curva algebraica en el plano euclidiano es el conjunto de los puntos cuyas coordenadas son las soluciones de una ecuación polinómica bivariada p ( x , y ) = 0. Esta ecuación a menudo se denomina ecuación implícita de la curva, en contraste con las curvas que son el gráfico de una función que define explícitamente y como una función de x .
Con una curva dada por una ecuación implícita de este tipo, los primeros problemas son determinar la forma de la curva y dibujarla. Estos problemas no son tan fáciles de resolver como en el caso del gráfico de una función, para el cual y puede calcularse fácilmente para varios valores de x . El hecho de que la ecuación definitoria sea un polinomio implica que la curva tiene algunas propiedades estructurales que pueden ayudar a resolver estos problemas.
Cada curva algebraica puede descomponerse de forma única en un número finito de arcos monótonos suaves (también llamados ramas ) a veces conectados por algunos puntos a veces llamados "puntos notables", y posiblemente un número finito de puntos aislados llamados acnodos . Un arco monótono suave es el gráfico de una función suave que está definida y es monótona en un intervalo abierto del eje x . En cada dirección, un arco es ilimitado (generalmente llamado arco infinito ) o tiene un punto final que es un punto singular (esto se definirá a continuación) o un punto con una tangente paralela a uno de los ejes de coordenadas.
Por ejemplo, para la cúbica de Tschirnhausen , hay dos arcos infinitos que tienen como punto final el origen (0,0). Este punto es el único punto singular de la curva. También hay dos arcos que tienen como punto final este punto singular y que tienen como segundo punto final una tangente horizontal. Finalmente, hay otros dos arcos que tienen como primer punto final uno de estos puntos con una tangente horizontal y como segundo punto final el único punto con una tangente vertical. En cambio, la senoide no es ciertamente una curva algebraica, ya que tiene un número infinito de arcos monótonos.
Para dibujar una curva algebraica es importante conocer los puntos destacables y sus tangentes, las ramas infinitas y sus asíntotas (si las hay) y la forma en que los arcos las conectan. También es útil considerar los puntos de inflexión como puntos destacables. Cuando toda esta información se dibuja en una hoja de papel, la forma de la curva suele aparecer con bastante claridad. Si no es así, basta con añadir algunos otros puntos y sus tangentes para obtener una buena descripción de la curva.
Los métodos para calcular los puntos notables y sus tangentes se describen a continuación en la sección Puntos notables de una curva plana.
Curvas proyectivas planas
A menudo es deseable considerar curvas en el espacio proyectivo . Una curva algebraica en el plano proyectivo o curva proyectiva plana es el conjunto de los puntos en un plano proyectivo cuyas coordenadas proyectivas son ceros de un polinomio homogéneo en tres variables P ( x , y , z ).
Toda curva algebraica afín de ecuación p ( x , y ) = 0 puede completarse en la curva proyectiva de ecuación donde es el resultado de la homogeneización de p . Por el contrario, si P ( x , y , z ) = 0 es la ecuación homogénea de una curva proyectiva, entonces P ( x , y , 1) = 0 es la ecuación de una curva afín, que consiste en los puntos de la curva proyectiva cuya tercera coordenada proyectiva no es cero. Estas dos operaciones son recíprocas entre sí, ya que y , si p está definida por , entonces tan pronto como el polinomio homogéneo P no es divisible por z .
Por ejemplo, la curva proyectiva de la ecuación x 2 + y 2 − z 2 es la completitud proyectiva del círculo unitario de la ecuación x 2 + y 2 − 1 = 0.
Esto implica que una curva afín y su compleción proyectiva son las mismas curvas o, más precisamente, que la curva afín es una parte de la curva proyectiva que es lo suficientemente grande como para definir bien la curva "completa". Este punto de vista se expresa comúnmente llamando "puntos en el infinito" de la curva afín a los puntos (en número finito) de la compleción proyectiva que no pertenecen a la parte afín.
Las curvas proyectivas se estudian frecuentemente por sí mismas. También son útiles para el estudio de curvas afines. Por ejemplo, si p ( x , y ) es el polinomio que define una curva afín, además de las derivadas parciales y , es útil considerar la derivada en el infinito.
Por ejemplo, la ecuación de la tangente de la curva afín de la ecuación p ( x , y ) = 0 en un punto ( a , b ) es
Puntos destacables de una curva plana
En esta sección, consideramos una curva algebraica plana definida por un polinomio bivariado p ( x , y ) y su completitud proyectiva, definida por la homogeneización de p .
Intersección con una línea
Conocer los puntos de intersección de una curva con una línea dada es a menudo útil. La intersección con los ejes de coordenadas y las asíntotas son útiles para dibujar la curva. La intersección con una línea paralela a los ejes permite encontrar al menos un punto en cada rama de la curva. Si se dispone de un algoritmo eficaz de búsqueda de raíces , esto permite dibujar la curva trazando el punto de intersección con todas las líneas paralelas al eje y y que pasan por cada píxel del eje x .
Si el polinomio que define la curva tiene un grado d , cualquier recta corta la curva en un máximo de d puntos. El teorema de Bézout afirma que este número es exactamente d , si se buscan los puntos en el plano proyectivo sobre un cuerpo algebraicamente cerrado (por ejemplo los números complejos ), y se cuentan con su multiplicidad . El método de cálculo que sigue demuestra nuevamente este teorema, en este caso simple.
Para calcular la intersección de la curva definida por el polinomio p con la recta de ecuación ax + by + c = 0, se resuelve la ecuación de la recta para x (o para y si a = 0). Sustituyendo el resultado en p , se obtiene una ecuación univariante q ( y ) = 0 (o q ( x ) = 0, si la ecuación de la recta ha sido resuelta en y ), cada una de cuyas raíces es una coordenada de un punto de intersección. La otra coordenada se deduce de la ecuación de la recta. La multiplicidad de un punto de intersección es la multiplicidad de la raíz correspondiente. Hay un punto de intersección en el infinito si el grado de q es menor que el grado de p ; la multiplicidad de dicho punto de intersección en el infinito es la diferencia de los grados de p y q .
Tangente en un punto
La tangente en un punto ( a , b ) de la curva es la recta de ecuación , como para toda curva diferenciable definida por una ecuación implícita. En el caso de los polinomios, otra fórmula para la tangente tiene un término constante más simple y es más simétrica:
donde es la derivada en el infinito. La equivalencia de las dos ecuaciones resulta del teorema de la función homogénea de Euler aplicado a P .
Si la tangente no está definida y el punto es un punto singular .
Esto se extiende inmediatamente al caso proyectivo: La ecuación de la tangente de en el punto de coordenadas proyectivas ( a : b : c ) de la curva proyectiva de ecuación P ( x , y , z ) = 0 es
y los puntos de las curvas que son singulares son los puntos tales que
(La condición P ( a , b , c ) = 0 está implícita en estas condiciones, por el teorema de la función homogénea de Euler.)
Asíntotas
A cada rama infinita de una curva algebraica le corresponde un punto en el infinito de la curva, es decir, un punto de terminación proyectiva de la curva que no pertenece a su parte afín. La asíntota correspondiente es la tangente de la curva en ese punto. La fórmula general para la tangente a una curva proyectiva puede aplicarse, pero en este caso conviene hacerla explícita.
Sea la descomposición del polinomio que define la curva en sus partes homogéneas, donde p i es la suma de los monomios de p de grado i . Se sigue que y
Un punto en el infinito de la curva es un cero de p de la forma ( a , b , 0). Equivalentemente, ( a , b ) es un cero de p d . El teorema fundamental del álgebra implica que, sobre un cuerpo algebraicamente cerrado (típicamente, el cuerpo de números complejos), p d se factoriza en un producto de factores lineales. Cada factor define un punto en el infinito sobre la curva: si bx − ay es tal factor, entonces define el punto en el infinito ( a , b , 0). Sobre los números reales, p d se factoriza en factores lineales y cuadráticos. Los factores cuadráticos irreducibles definen puntos no reales en el infinito, y los puntos reales están dados por los factores lineales. Si ( a , b , 0) es un punto en el infinito de la curva, se dice que ( a , b ) es una dirección asintótica . Fijando q = p d la ecuación de la asíntota correspondiente es
Si y la asíntota es la recta en el infinito, y, en el caso real, la curva tiene una rama que parece una parábola . En este caso se dice que la curva tiene una rama parabólica . Si la curva tiene un punto singular en el infinito y puede tener varias asíntotas. Se pueden calcular mediante el método de cálculo del cono tangente de un punto singular.
Puntos singulares
Los puntos singulares de una curva de grado d definida por un polinomio p ( x , y ) de grado d son las soluciones del sistema de ecuaciones: En característica cero , este sistema es equivalente a donde, con la notación del apartado precedente, Los sistemas son equivalentes por el teorema de la función homogénea de Euler . Este último sistema tiene la ventaja de tener su tercer polinomio de grado d -1 en lugar de d .
De manera similar, para una curva proyectiva definida por un polinomio homogéneo P ( x , y , z ) de grado d , los puntos singulares tienen como coordenadas homogéneas las soluciones del sistema . (En la característica positiva, la ecuación debe agregarse al sistema.)
Esto implica que el número de puntos singulares es finito siempre que p ( x , y ) o P ( x , y , z ) esté libre de cuadrados . El teorema de Bézout implica, por tanto, que el número de puntos singulares es como máximo ( d − 1) 2 , pero este límite no es preciso porque el sistema de ecuaciones está sobredeterminado . Si se permiten polinomios reducibles , el límite preciso es d ( d − 1)/2, este valor se alcanza cuando el polinomio se factoriza en factores lineales, es decir, si la curva es la unión de d líneas. Para curvas y polinomios irreducibles, el número de puntos singulares es como máximo ( d − 1)( d − 2)/2, debido a la fórmula que expresa el género en términos de las singularidades (véase más abajo). El máximo lo alcanzan las curvas de género cero cuyas singularidades tienen todas multiplicidad dos y tangentes distintas (véase más abajo).
La ecuación de las tangentes en un punto singular está dada por la parte homogénea no nula del grado más bajo de la serie de Taylor del polinomio en el punto singular. Cuando se cambian las coordenadas para poner el punto singular en el origen, la ecuación de las tangentes en el punto singular es, por tanto, la parte homogénea no nula del grado más bajo del polinomio, y la multiplicidad del punto singular es el grado de esta parte homogénea.
Estructura analítica
El estudio de la estructura analítica de una curva algebraica en las proximidades de un punto singular proporciona información precisa sobre la topología de las singularidades. De hecho, cerca de un punto singular, una curva algebraica real es la unión de un número finito de ramas que se cortan sólo en el punto singular y tienen la apariencia de una cúspide o de una curva suave.
Cerca de un punto regular, una de las coordenadas de la curva puede expresarse como una función analítica de la otra coordenada. Este es un corolario del teorema de la función implícita analítica e implica que la curva es suave cerca del punto. Cerca de un punto singular, la situación es más complicada e involucra series de Puiseux , que proporcionan ecuaciones paramétricas analíticas de las ramas.
Para describir una singularidad, conviene trasladar la curva para que la singularidad esté en el origen. Esto consiste en un cambio de variable de la forma donde son las coordenadas del punto singular. En lo sucesivo, se supone que el punto singular en consideración siempre está en el origen.
La ecuación de una curva algebraica es donde f es un polinomio en x e y . Este polinomio puede considerarse como un polinomio en y , con coeficientes en el cuerpo algebraicamente cerrado de la serie de Puiseux en x . Por lo tanto, f puede factorizarse en factores de la forma donde P es una serie de Puiseux. Estos factores son todos diferentes si f es un polinomio irreducible , porque esto implica que f es libre de cuadrados , una propiedad que es independiente del cuerpo de coeficientes.
Las series de Puiseux que aparecen aquí tienen la forma donde d es un entero positivo, y es un entero que también puede suponerse positivo, porque consideramos solo las ramas de la curva que pasan por el origen. Sin pérdida de generalidad, podemos suponer que d es coprimo con el máximo común divisor de n tal que (de lo contrario, se podría elegir un denominador común más pequeño para los exponentes).
Sea una raíz d primitiva de la unidad . Si la serie de Puiseux anterior aparece en la factorización de , entonces la serie d aparece también en la factorización (una consecuencia de la teoría de Galois ). Estas series d se denominan conjugadas , y se consideran como una sola rama de la curva, de índice de ramificación d .
En el caso de una curva real, es decir, una curva definida por un polinomio con coeficientes reales, pueden darse tres casos. Si ninguna tiene coeficientes reales, entonces se tiene una rama no real. Si alguna tiene coeficientes reales, entonces se puede elegir como . Si d es impar, entonces cada valor real de x proporciona un valor real de , y se tiene una rama real que parece regular, aunque es singular si d > 1 . Si d es par, entonces y tienen valores reales, pero solo para x ≥ 0 . En este caso, la rama real parece una cúspide (o es una cúspide, dependiendo de la definición de cúspide que se use).
Por ejemplo, la cúspide ordinaria tiene una sola rama. Si se define por la ecuación , entonces la factorización es el índice de ramificación es 2, y los dos factores son reales y definen cada uno una media rama. Si se rota la cúspide, la ecuación se convierte en y la factorización es con (el coeficiente no se ha simplificado a j para mostrar cómo la definición anterior de está especializada). Aquí el índice de ramificación es 3, y solo un factor es real; esto muestra que, en el primer caso, los dos factores deben considerarse como definitorios de la misma rama.
Curvas algebraicas no planas
Una curva algebraica es una variedad algebraica de dimensión uno. Esto implica que una curva afín en un espacio afín de dimensión n está definida por, al menos, n − 1 polinomios en n variables. Para definir una curva, estos polinomios deben generar un ideal primo de dimensión 1 en el sentido de Krull . Esta condición no es fácil de comprobar en la práctica. Por lo tanto, puede ser preferible la siguiente forma de representar curvas no planas.
Sean n polinomios de dos variables x 1 y x 2 tales que f es irreducible. Los puntos en el espacio afín de dimensión n cuyas coordenadas satisfacen las ecuaciones e inecuaciones
son todos los puntos de una curva algebraica en la que se han eliminado un número finito de puntos. Esta curva está definida por un sistema de generadores del ideal de los polinomios h tales que existe un entero k tal que pertenece al ideal generado por . Esta representación es una equivalencia biracional entre la curva y la curva plana definida por f . Toda curva algebraica puede representarse de esta manera. Sin embargo, puede ser necesario un cambio lineal de variables para hacer casi siempre inyectiva la proyección sobre las dos primeras variables. Cuando se necesita un cambio de variables, casi cualquier cambio es conveniente, siempre que esté definido sobre un cuerpo infinito.
Esta representación nos permite deducir fácilmente cualquier propiedad de una curva algebraica no plana, incluida su representación gráfica, a partir de la propiedad correspondiente de su proyección plana.
Para una curva definida por sus ecuaciones implícitas, la representación anterior de la curva puede deducirse fácilmente a partir de una base de Gröbner para un ordenamiento de bloques tal que el bloque de las variables más pequeñas es ( x 1 , x 2 ). El polinomio f es el único polinomio en la base que depende sólo de x 1 y x 2 . Las fracciones g i / g 0 se obtienen eligiendo, para i = 3, ..., n , un polinomio en la base que sea lineal en x i y dependa sólo de x 1 , x 2 y x i . Si estas elecciones no son posibles, esto significa que o bien las ecuaciones definen un conjunto algebraico que no es una variedad, o que la variedad no es de dimensión uno, o que hay que cambiar de coordenadas. El último caso se da cuando f existe y es único, y, para i = 3, …, n , existen polinomios cuyo monomio principal depende sólo de x 1 , x 2 y x i .
Campos de funciones algebraicas
El estudio de las curvas algebraicas puede reducirse al estudio de las curvas algebraicas irreducibles : aquellas curvas que no pueden escribirse como la unión de dos curvas menores. Hasta la equivalencia biracional , las curvas irreducibles sobre un cuerpo F son categóricamente equivalentes a cuerpos de funciones algebraicas en una variable sobre F . Un cuerpo de funciones algebraicas de este tipo es una extensión de cuerpo K de F que contiene un elemento x que es trascendental sobre F , y tal que K es una extensión algebraica finita de F ( x ), que es el cuerpo de funciones racionales en el indeterminado x sobre F .
Por ejemplo, considere el campo C de números complejos, sobre el cual podemos definir el campo C ( x ) de funciones racionales en C . Si y 2 = x 3 − x − 1 , entonces el campo C ( x , y ) es un campo de funciones elípticas . El elemento x no está determinado de manera unívoca; el campo también puede considerarse, por ejemplo, como una extensión de C ( y ). La curva algebraica correspondiente al campo de funciones es simplemente el conjunto de puntos ( x , y ) en C 2 que satisfacen y 2 = x 3 − x − 1 .
Si el cuerpo F no es algebraicamente cerrado, el punto de vista de los cuerpos de funciones es un poco más general que el de considerar el lugar geométrico de los puntos, ya que incluimos, por ejemplo, "curvas" sin puntos sobre ellas. Por ejemplo, si el cuerpo base F es el cuerpo R de números reales, entonces x 2 + y 2 = −1 define un cuerpo de extensión algebraica de R ( x ), pero la curva correspondiente considerada como un subconjunto de R 2 no tiene puntos. La ecuación x 2 + y 2 = −1 sí define una curva algebraica irreducible sobre R en el sentido del esquema (una integral , esquemas unidimensionales separados de tipo finito sobre R ). En este sentido, la correspondencia uno a uno entre curvas algebraicas irreducibles sobre F (hasta equivalencia biracional) y cuerpos de funciones algebraicas en una variable sobre F se cumple en general.
Dos curvas pueden ser birracionalmente equivalentes (es decir, tener campos de funciones isomorfos ) sin ser isomorfas como curvas. La situación se vuelve más fácil cuando se trata de curvas no singulares , es decir, aquellas que carecen de singularidades. Dos curvas proyectivas no singulares sobre un campo son isomorfas si y solo si sus campos de funciones son isomorfos.
El teorema de Tsen trata del campo funcional de una curva algebraica sobre un campo algebraicamente cerrado.
Curvas complejas y superficies reales
Una curva algebraica proyectiva compleja reside en un espacio proyectivo complejo n -dimensional CP n . Este tiene dimensión compleja n , pero dimensión topológica, como variedad real , 2 n , y es compacta , conexa y orientable . Una curva algebraica sobre C tiene asimismo dimensión topológica dos; en otras palabras, es una superficie .
El género topológico de esta superficie, es decir, el número de asas o agujeros de rosquilla, es igual al género geométrico de la curva algebraica que se puede calcular por medios algebraicos. En resumen, si se considera una proyección plana de una curva no singular que tiene grado d y solo singularidades ordinarias (singularidades de multiplicidad dos con tangentes distintas), entonces el género es ( d − 1)( d − 2)/2 − k , donde k es el número de estas singularidades.
Superficies compactas de Riemann
Una superficie de Riemann es una variedad analítica compleja conexa de una dimensión compleja, lo que la convierte en una variedad real conexa de dos dimensiones. Es compacta si es compacta como espacio topológico.
Existe una triple equivalencia de categorías entre la categoría de curvas algebraicas proyectivas irreducibles suaves sobre C (con morfismos regulares no constantes ), la categoría de superficies de Riemann compactas (con morfismos holomorfos no constantes ) y la opuesta de la categoría de cuerpos de funciones algebraicas en una variable sobre C (con homomorfismos de cuerpo que fijan C como morfismos). Esto significa que al estudiar estos tres temas estamos en cierto sentido estudiando una y la misma cosa. Permite utilizar métodos analíticos complejos en geometría algebraica, y métodos geométricos algebraicos en análisis complejo y métodos teóricos de campos en ambos. Esto es característico de una clase mucho más amplia de problemas en geometría algebraica.
Véase también geometría algebraica y geometría analítica para una teoría más general.
Singularidades
Utilizando el concepto intrínseco de espacio tangente , los puntos P en una curva algebraica C se clasifican como suaves (sinónimo: no singulares ), o bien singulares . Dados n − 1 polinomios homogéneos en n + 1 variables, podemos encontrar la matriz jacobiana como la matriz ( n − 1)×( n + 1) de las derivadas parciales. Si el rango de esta matriz es n − 1, entonces los polinomios definen una curva algebraica (de lo contrario, definen una variedad algebraica de mayor dimensión). Si el rango permanece n − 1 cuando la matriz jacobiana se evalúa en un punto P en la curva, entonces el punto es un punto suave o regular; de lo contrario, es un punto singular . En particular, si la curva es una curva algebraica proyectiva plana, definida por una única ecuación polinomial homogénea f ( x , y , z ) = 0, entonces los puntos singulares son precisamente los puntos P donde el rango de la matriz 1×( n + 1) es cero, es decir, donde
Como f es un polinomio, esta definición es puramente algebraica y no hace ninguna suposición sobre la naturaleza del cuerpo F , que en particular no necesita ser un número real o complejo. Por supuesto, debe recordarse que (0,0,0) no es un punto de la curva y, por lo tanto, no es un punto singular.
De manera similar, para una curva algebraica afín definida por una única ecuación polinomial f ( x , y ) = 0, entonces los puntos singulares son precisamente los puntos P de la curva donde el rango de la matriz jacobiana 1× n es cero, es decir, donde
Las singularidades de una curva no son invariantes biracionales. Sin embargo, localizar y clasificar las singularidades de una curva es una forma de calcular el género , que es un invariante biracional. Para que esto funcione, debemos considerar la curva de manera proyectiva y exigir que F sea algebraicamente cerrado, de modo que se consideren todas las singularidades que pertenecen a la curva.
Clasificación de singularidades

Los puntos singulares incluyen múltiples puntos donde la curva se cruza consigo misma, y también varios tipos de cúspides , por ejemplo la que muestra la curva con ecuación x3 = y2 en (0,0).
Una curva C tiene como máximo un número finito de puntos singulares. Si no tiene ninguno, se la puede llamar suave o no singular . Comúnmente, esta definición se entiende sobre un cuerpo algebraicamente cerrado y para una curva C en un espacio proyectivo (es decir, completo en el sentido de la geometría algebraica). Por ejemplo, la curva plana de ecuación se considera como singular, por tener un punto singular (una cúspide) en el infinito.
En el resto de esta sección, se considera una curva plana C definida como el conjunto cero de un polinomio bivariado f ( x , y ) . Algunos de los resultados, pero no todos, pueden generalizarse a curvas no planas.
Los puntos singulares se clasifican mediante varios invariantes. La multiplicidad m se define como el entero máximo tal que las derivadas de f a todos los órdenes hasta m – 1 se anulan (también el número mínimo de intersección entre la curva y una línea recta en P ). Intuitivamente, un punto singular tienedelta invariante δsi concentraδpuntos dobles ordinarios en P . Para hacer esto preciso, elde explosiónproduce los llamadospuntos infinitamente cercanos, y sumando m ( m − 1)/2sobre los puntos infinitamente cercanos, dondemes su multiplicidad, produceδ. Para una curva irreducible y reducida y un punto P podemos definirδalgebraicamente como la longitud dedondees el anillo local enPyes su cierre integral.[1]
El número de Milnor μ de una singularidad es el grado de la aplicación grado f ( x , y )/|grad f ( x , y )| en la pequeña esfera de radio ε, en el sentido del grado topológico de una aplicación continua , donde grad f es el campo vectorial gradiente (complejo) de f . Está relacionado con δ y r por la fórmula de Milnor–Jung,
Aquí, el número de ramificaciones r de P es el número de ramas irreducibles localmente en P . Por ejemplo, r = 1 en una cúspide ordinaria, y r = 2 en un punto doble ordinario. La multiplicidad m es al menos r , y P es singular si y solo si m es al menos 2. Además, δ es al menos m ( m -1)/2.
Calcular los invariantes delta de todas las singularidades permite determinar el género g de la curva; si d es el grado, entonces
donde la suma se toma sobre todos los puntos singulares P de la curva plana proyectiva compleja. Se llama fórmula de género .
Asignar los invariantes [ m , δ, r ] a una singularidad, donde m es la multiplicidad, δ es el delta-invariante y r es el número de ramificación. Entonces, una cúspide ordinaria es un punto con invariantes [2,1,1] y un punto doble ordinario es un punto con invariantes [2,1,2], y un punto m -múltiple ordinario es un punto con invariantes [ m , m ( m − 1)/2, m ].
Ejemplos de curvas
Curvas racionales
Una curva racional , también llamada curva unicursal, es cualquier curva que es biracionalmente equivalente a una línea, que podemos tomar como una línea proyectiva; en consecuencia, podemos identificar el campo de funciones de la curva con el campo de funciones racionales en una indeterminada F ( x ). Si F es algebraicamente cerrada, esto es equivalente a una curva de género cero; sin embargo, el campo de todas las funciones algebraicas reales definidas en la variedad algebraica real x 2 + y 2 = −1 es un campo de género cero que no es un campo de funciones racionales.
Concretamente, una curva racional inserta en un espacio afín de dimensión n sobre F puede parametrizarse (salvo puntos excepcionales aislados) mediante n funciones racionales de un único parámetro t ; reduciendo estas funciones racionales al mismo denominador, los n + 1 polinomios resultantes definen una parametrización polinómica de la completitud proyectiva de la curva en el espacio proyectivo. Un ejemplo es la curva normal racional , donde todos estos polinomios son monomios .
Cualquier sección cónica definida sobre F con un punto racional en F es una curva racional. Se puede parametrizar trazando una línea con pendiente t a través del punto racional y una intersección con la curva cuadrática plana; esto da un polinomio con coeficientes F -racionales y una raíz F -racional, por lo tanto, la otra raíz también es F -racional (es decir, pertenece a F ).
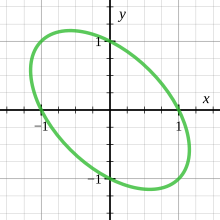
Por ejemplo, considere la elipse x 2 + xy + y 2 = 1, donde (−1, 0) es un punto racional. Trazando una línea con pendiente t desde (−1,0), y = t ( x + 1 ), sustituyéndola en la ecuación de la elipse, factorizando y despejando x , obtenemos
Entonces la ecuación para y es
que define una parametrización racional de la elipse y, por lo tanto, muestra que la elipse es una curva racional. Se dan todos los puntos de la elipse, excepto (−1,1), que corresponde a t = ∞; por lo tanto, toda la curva está parametrizada por la línea proyectiva real.
Una parametrización racional de este tipo puede considerarse en el espacio proyectivo equiparando las primeras coordenadas proyectivas a los numeradores de la parametrización y las últimas al denominador común. Como el parámetro está definido en una línea proyectiva, los polinomios en el parámetro deben homogeneizarse . Por ejemplo, la parametrización proyectiva de la elipse anterior es
Eliminando T y U entre estas ecuaciones obtenemos nuevamente la ecuación proyectiva de la elipse que puede obtenerse fácilmente de manera directa homogeneizando la ecuación anterior.
Muchas de las curvas de la lista de curvas de Wikipedia son racionales y, por lo tanto, tienen parametrizaciones racionales similares.
Curvas del plano racional
Las curvas planas racionales son curvas racionales incrustadas en . Dadas secciones genéricas de polinomios homogéneos de grado en dos coordenadas, , hay un mapa dado por definir una curva plana racional de grado . [2] Hay un espacio de módulos asociado (donde es la clase de hiperplano) que parametriza todas esas curvas estables . Se puede hacer un recuento de dimensiones para determinar la dimensión de los espacios de módulos: Hay parámetros en dando el total de parámetros para cada una de las secciones. Entonces, dado que se consideran hasta un cociente proyectivo en hay menos parámetro en . Además, hay un grupo tridimensional de automorfismos de , por lo tanto tiene dimensión . Este espacio de módulos se puede usar para contar el número de curvas planas racionales de grado que intersecan puntos usando la teoría de Gromov-Witten . [3] Está dado por la relación recursiva donde .
Curvas elípticas
Una curva elíptica puede definirse como cualquier curva de género uno con un punto racional : un modelo común es una curva cúbica no singular , que basta para modelar cualquier curva de género uno. En este modelo, el punto distinguido se considera comúnmente un punto de inflexión en el infinito; esto equivale a exigir que la curva pueda escribirse en forma de Tate-Weierstrass, que en su versión proyectiva es
Si la característica del campo es diferente de 2 y 3, entonces un cambio lineal de coordenadas permite poner lo que da la forma clásica de Weierstrass
Las curvas elípticas tienen la estructura de un grupo abeliano con el punto distinguido como identidad de la ley del grupo. En un modelo cúbico plano, tres puntos suman cero en el grupo si y solo si son colineales . Para una curva elíptica definida sobre los números complejos, el grupo es isomorfo al grupo aditivo del plano complejo módulo la red de períodos de las funciones elípticas correspondientes .
La intersección de dos superficies cuadráticas es, en general, una curva no singular de género uno y grado cuatro, y por tanto una curva elíptica, si tiene un punto racional. En casos especiales, la intersección puede ser una curva cuártica singular racional o puede descomponerse en curvas de grados menores que no siempre son distintas (ya sea una curva cúbica y una recta, o dos cónicas, o una cónica y dos rectas, o cuatro rectas).
Curvas de género mayor que uno
Las curvas de género mayor que uno difieren notablemente de las curvas racionales y elípticas. Dichas curvas definidas sobre los números racionales, por el teorema de Faltings , pueden tener solo un número finito de puntos racionales, y pueden considerarse como si tuvieran una estructura de geometría hiperbólica . Algunos ejemplos son las curvas hiperelípticas , la curva cuártica de Klein y la curva de Fermat x n + y n = z n cuando n es mayor que tres. También las curvas planas proyectivas en y las curvas en proporcionan muchos ejemplos útiles.
Curvas planas proyectivas
Las curvas planas de grado , que se pueden construir como el lugar geométrico de desaparición de una sección genérica , tienen un género que se puede calcular utilizando la cohomología de haces coherentes . A continuación se presenta un breve resumen de los géneros de las curvas en relación con su grado
| grado | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| género | 0 | 0 | 1 | 3 | 6 | 10 | 15 |
Por ejemplo, la curva define una curva de género que es suave ya que las diferenciales no tienen ceros comunes con la curva. Un no-ejemplo de una sección genérica es la curva que, por el teorema de Bezouts , debe intersecar en la mayoría de los puntos, es la unión de dos curvas racionales que se intersecan en dos puntos. Nota está dada por el lugar geométrico de desaparición de y está dada por el lugar geométrico de desaparición de . Estos se pueden encontrar explícitamente: un punto se encuentra en ambos si . Entonces las dos soluciones son los puntos tales que , que son y .
Curvas en producto de rectas proyectivas
La curva dada por el lugar geométrico de desaparición de , para , da curvas de género que se pueden comprobar utilizando la cohomología de haces coherentes . Si , entonces definen curvas de género , por lo tanto, una curva de cualquier género se puede construir como una curva en . Sus géneros se pueden resumir en la tabla
| Bigrado | ||||
|---|---|---|---|---|
| género | 1 | 2 | 3 | 4 |
y para , esto es
| Bigrado | ||||
|---|---|---|---|---|
| género | 2 | 4 | 6 | 8 |
Véase también
Geometría algebraica clásica
Geometría algebraica moderna
- Geometría birracional
- Sección cónica
- Curva elíptica
- Ideal fraccionario
- Campo de funciones de una variedad algebraica
- Campo de funciones (teoría de esquemas)
- Género (matemáticas)
- Lemniscata polinómica
- Curva plana cuártica
- Curva normal racional
- Teorema de Riemann-Roch para curvas algebraicas
- Teorema de Weber (Curvas algebraicas)
Geometría de las superficies de Riemann
Notas
- ^ Hartshorne, Geometría algebraica, IV Ex. 1.8.
- ^ Kazaryan, Maxim E.; Lando, Sergei K.; Prasolov, Victor (2018). Curvas algebraicas: hacia espacios de módulos. Conferencias de Moscú. Springer International Publishing. págs. 213-214. ISBN 978-3-030-02942-5.
- ^ "Fórmula de Kontsevich para curvas racionales planas" (PDF) . Archivado (PDF) del original el 26 de febrero de 2020.
Referencias
- Brieskorn, Egbert; Knörrer, Horst (2013). Curvas algebraicas planas. Traducido por Stillwell, John. Birkhäuser. ISBN 978-3-0348-5097-1.
- Chevalley, Claude (1951). Introducción a la teoría de funciones algebraicas de una variable. Encuestas matemáticas. Vol. 6. American Mathematical Society. ISBN 978-0-8218-1506-9.
- Coolidge, Julian L. (2004) [1931]. Tratado sobre curvas planas algebraicas. Dover. ISBN 978-0-486-49576-7.
- Farkas, HM; Kra, I. (2012) [1980]. Superficies de Riemann. Textos de posgrado en matemáticas. Vol. 71. Springer. ISBN 978-1-4684-9930-8.
- Fulton, William (1989). Curvas algebraicas: Introducción a la geometría algebraica. Serie de apuntes de matemáticas. Vol. 30 (3.ª ed.). Addison-Wesley. ISBN 978-0-201-51010-2.
- Gibson, CG (1998). Geometría elemental de curvas algebraicas: una introducción para estudiantes de grado. Cambridge University Press. ISBN 978-0-521-64641-3.
- Griffiths, Phillip A. (1985). Introducción a las curvas algebraicas . Traducción de monografías matemáticas. Vol. 70 (3.ª ed.). Sociedad matemática estadounidense. ISBN 9780821845370.
- Hartshorne, Robin (2013) [1977]. Geometría algebraica. Textos de posgrado en matemáticas. Vol. 52. Springer. ISBN 978-1-4757-3849-0.
- Iitaka, Shigeru (2011) [1982]. Geometría algebraica: Introducción a la geometría birracional de variedades algebraicas. Textos de posgrado en matemáticas. Vol. 76. Springer Nueva York. ISBN 978-1-4613-8121-1.
- Milnor, John (1968). Puntos singulares de hipersuperficies complejas. Princeton University Press. ISBN 0-691-08065-8.
- Serre, Jean-Pierre (2012) [1988]. Grupos algebraicos y cuerpos de clases. Textos de posgrado en matemáticas. Vol. 117. Springer. ISBN 978-1-4612-1035-1.
- Kötter, Ernst (1887). "Grundzüge einer rein geometrischen Theorie der algebraischen ebenen Curven" [Fundamentos de una teoría puramente geométrica de curvas planas algebraicas]. Transacciones de la Real Academia de Berlín .— ganó el premio de la Academia en 1886 [1]
- ^ Norman Fraser (febrero de 1888). "Geometría sintética de curvas algebraicas de Kötter". Actas de la Sociedad Matemática de Edimburgo . 7 : 46–61, véase pág. 46.




































































![{\displaystyle s([x:y])=[s_{1}([x:y]):s_{2}([x:y]):s_{3}([x:y])]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e476e20e081b9270d1001c4c42230b194823854)
![{\displaystyle {\mathcal {M}}={\overline {\mathcal {M}}}_{0,0}(\mathbb {P} ^{2},d\cdot [H])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87b2550036885371874a4d33da2f543a1bb333d8)
![{\estilo de visualización [H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d2226487b5eb5f8a607d7233b5825b05775db6)






























![{\estilo de visualización [0:y:z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b33585ed1c64c143f7100a2d1dcde99525a8c0e2)

![{\displaystyle [0:1:-{\sqrt {-1}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d33353843fae9668cf937f167738e00196b3384)
![{\displaystyle [0:1:{\sqrt {-1}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3834a4be0b90e81063c32e3f083809a311fe1db)















