Experimentos de dispersión de Rutherford

Los experimentos de dispersión de Rutherford fueron una serie de experimentos que marcaron un hito y que permitieron a los científicos descubrir que cada átomo tiene un núcleo en el que se concentra toda su carga positiva y la mayor parte de su masa. Lo dedujeron tras medir cómo se dispersa un haz de partículas alfa cuando choca contra una lámina fina de metal . Los experimentos fueron realizados entre 1906 y 1913 por Hans Geiger y Ernest Marsden bajo la dirección de Ernest Rutherford en los Laboratorios de Física de la Universidad de Manchester .

El fenómeno físico fue explicado por Rutherford en un artículo clásico de 1911 que eventualmente condujo al uso generalizado de la dispersión en física de partículas para estudiar la materia subatómica. La dispersión de Rutherford o dispersión de Coulomb es la dispersión elástica de partículas cargadas por la interacción de Coulomb . El artículo también inició el desarrollo del modelo planetario de Rutherford del átomo y, finalmente, el modelo de Bohr .

La comunidad científica de los materiales ahora utiliza la dispersión de Rutherford en una técnica analítica llamada retrodispersión de Rutherford .

El modelo predominante de la estructura atómica antes de los experimentos de Rutherford fue ideado por J. J. Thomson . ^{[1] : 123} Thomson había descubierto el electrón a través de su trabajo sobre los rayos catódicos ^[2] y propuso que existían dentro de los átomos, y una corriente eléctrica son electrones saltando de un átomo a uno adyacente en una serie. Lógicamente tenía que haber una cantidad proporcional de carga positiva para equilibrar la carga negativa de los electrones y mantenerlos juntos. Al no tener idea de cuál era la fuente de esta carga positiva, propuso tentativamente que la carga positiva estaba en todas partes en el átomo, adoptando una forma esférica para simplificar. ^{[1] : 123  [3]} Thomson imaginó que el equilibrio de las fuerzas electrostáticas distribuiría los electrones a lo largo de esta esfera de una manera más o menos uniforme. Thomson también creía que los electrones podían moverse en esta esfera, y en ese sentido comparó la sustancia de la esfera con un líquido. ^[4] De hecho, la esfera positiva era más una abstracción que algo material.

Thomson nunca fue capaz de desarrollar un modelo completo y estable que pudiera predecir cualquiera de las otras propiedades conocidas del átomo, como los espectros de emisión y las valencias. ^[5] El científico japonés Hantaro Nagaoka rechazó el modelo de Thomson con el argumento de que las cargas opuestas no pueden penetrarse entre sí. ^[6] En cambio, propuso que los electrones orbitan la carga positiva como los anillos alrededor de Saturno . ^[7] Sin embargo, también se sabía que este modelo era inestable. ^{[8] : 303}

Una partícula alfa es una partícula de materia con carga positiva que se emite espontáneamente a partir de ciertos elementos radiactivos. Las partículas alfa son tan pequeñas que son invisibles, pero se pueden detectar con el uso de pantallas fosforescentes, placas fotográficas o electrodos. Rutherford las descubrió en 1899. ^[9] En 1906, al estudiar cómo los rayos de partículas alfa son desviados por los campos magnéticos y eléctricos, dedujo que eran esencialmente átomos de helio despojados de dos electrones. ^[10] Thomson y Rutherford no sabían nada sobre la estructura interna de las partículas alfa. Antes de 1911 se pensaba que tenían un diámetro similar al de los átomos de helio y que contenían aproximadamente diez electrones. ^{[8] :  280}

El modelo de Thomson era coherente con la evidencia experimental disponible en ese momento. Thomson estudió la dispersión de partículas beta que mostró pequeñas desviaciones angulares modeladas como interacciones de la partícula con muchos átomos en sucesión. Cada interacción de la partícula con los electrones del átomo y la esfera de fondo positiva conduciría a una pequeña desviación, pero muchas de esas colisiones podrían sumarse. ^{[8] : 274} Se esperaba que la dispersión de partículas alfa fuera similar. ^{[8] :  281} El equipo de Rutherford demostraría que el modelo de dispersión múltiple no era necesario: la dispersión única de una carga compacta en el centro del átomo explicaría todos los datos de dispersión. ^{[8] : 289}

Ernest Rutherford fue profesor Langworthy de Física en la Universidad Victoria de Manchester ^{[11] : 188} (ahora la Universidad de Manchester ). Ya había recibido numerosos honores por sus estudios sobre la radiación. Había descubierto la existencia de rayos alfa , rayos beta y rayos gamma , y ​​había demostrado que estos eran consecuencia de la desintegración de los átomos . En 1906, recibió la visita del físico alemán Hans Geiger , y quedó tan impresionado que le pidió a Geiger que se quedara y lo ayudara con su investigación. Ernest Marsden era un estudiante de física que estudiaba con Geiger. ^[12]

En 1908, Rutherford intentó determinar de forma independiente la carga y la masa de las partículas alfa. Para ello, quería contar el número de partículas alfa y medir su carga total; la relación daría la carga de una sola partícula alfa. Las partículas alfa son demasiado pequeñas para verlas, pero Rutherford sabía por el trabajo de JS Townsend en 1902 que las partículas alfa ionizan las moléculas del aire y, si el aire está dentro de un campo eléctrico intenso, cada ion producirá una cascada de iones que darán un pulso de corriente eléctrica. Basándose en este principio, Rutherford y Geiger diseñaron un dispositivo de conteo simple que consistía en dos electrodos en un tubo de vidrio. (Véase el experimento nº 1908). Cada partícula alfa que pasara por el tubo crearía un pulso de electricidad que podría contarse. Era una versión temprana del contador Geiger . ^{[8] : 261}

El contador que construyeron Geiger y Rutherford resultó poco fiable porque las partículas alfa se desviaban con demasiada fuerza en sus colisiones con las moléculas de aire dentro de la cámara de detección. Las trayectorias altamente variables de las partículas alfa significaban que no todas generaban la misma cantidad de iones a medida que pasaban a través del gas, lo que producía lecturas erráticas. Esto desconcertó a Rutherford porque había pensado que las partículas alfa eran demasiado pesadas para ser desviadas con tanta fuerza. Rutherford le pidió a Geiger que investigara hasta qué punto la materia podía dispersar los rayos alfa. ^[13]

Los experimentos que diseñaron implicaron bombardear una lámina de metal con un haz de partículas alfa para observar cómo la lámina las dispersaba en relación con su espesor y material. Utilizaron una pantalla fosforescente para medir las trayectorias de las partículas. Cada impacto de una partícula alfa en la pantalla produjo un pequeño destello de luz. Geiger trabajó en un laboratorio a oscuras durante horas y horas, contando estos pequeños destellos utilizando un microscopio. ^[14] Para la lámina de metal, probaron una variedad de metales, pero favorecieron el oro porque podían hacer que la lámina fuera muy delgada, ya que el oro es el metal más maleable. ^{[15] : 127} Como fuente de partículas alfa, la sustancia elegida por Rutherford fue el radio , que es miles de veces más radiactivo que el uranio. ^[16]

En un experimento de 1909, Geiger y Marsden descubrieron que las láminas de metal podían dispersar algunas partículas alfa en todas direcciones, a veces más de 90°. ^{[17] : 4} Esto debería haber sido imposible según el modelo de Thomson. ^{[17] : 4} Según el modelo de Thomson, todas las partículas alfa deberían haber pasado directamente.

En el modelo atómico de Thomson, la esfera de carga positiva que llena el átomo y encapsula los electrones es permeable; después de todo, los electrones podrían moverse en ella. Por lo tanto, una partícula alfa debería poder pasar a través de esta esfera si las fuerzas electrostáticas en su interior lo permiten. El propio Thomson no estudió cómo una partícula alfa podría dispersarse en una colisión de este tipo con un átomo, pero sí estudió la dispersión de partículas beta . ^{[8] : 277} Calculó que una partícula beta solo experimentaría una desviación muy pequeña al pasar a través de un átomo, ^[18] e incluso después de pasar a través de muchos átomos seguidos, la desviación total aún debería ser menor a 1°. ^[19] Las partículas alfa suelen tener mucho más momento que las partículas beta y, por lo tanto, también deberían experimentar solo la desviación más leve. ^[20]

La dispersión extrema observada obligó a Rutherford a revisar el modelo del átomo. ^{[21] : 25} El problema en el modelo de Thomson era que las cargas eran demasiado difusas para producir una fuerza electrostática lo suficientemente fuerte como para causar tal repulsión. Por lo tanto, tenían que estar más concentradas. En el nuevo modelo de Rutherford, la carga positiva no llena todo el volumen del átomo, sino que constituye un núcleo diminuto al menos 10.000 veces más pequeño que el átomo en su conjunto. Toda esa carga positiva concentrada en un volumen mucho más pequeño produce un campo eléctrico mucho más fuerte cerca de su superficie. El núcleo también transportaba la mayor parte de la masa del átomo. Esto significaba que podía desviar partículas alfa hasta 180° dependiendo de lo cerca que pasaran. Los electrones rodean este núcleo, repartidos por todo el volumen del átomo. Debido a que su carga negativa es difusa y su masa combinada es baja, tienen un efecto insignificante sobre la partícula alfa. ^[22]

Para verificar su modelo, Rutherford desarrolló un modelo científico para predecir la intensidad de las partículas alfa en los diferentes ángulos en que se dispersaban al salir de la lámina de oro, suponiendo que toda la carga positiva estaba concentrada en el centro del átomo. Este modelo fue validado en un experimento realizado en 1913. Su modelo explicaba tanto los resultados de dispersión beta de Thomson como los resultados de dispersión alfa de Geiger y Marsden. ^{[8] : 285}

En los primeros años, el ahora famoso artículo de Rutherford de 1911 generó pocas reacciones. ^{[11] : 192} El artículo trataba principalmente sobre la dispersión de partículas alfa en una era anterior a que la dispersión de partículas fuera una herramienta fundamental para la física. Las técnicas de probabilidad que utilizó y la confusa recopilación de observaciones involucradas no resultaron inmediatamente convincentes. ^{[8] : 304}

Los primeros impactos fueron para alentar un nuevo enfoque en los experimentos de dispersión. Por ejemplo, los primeros resultados de una cámara de nubes , por CTR Wilson muestran dispersión de partículas alfa y también aparecieron en 1911. ^{[23] [8] : 302} Con el tiempo, la dispersión de partículas se convirtió en un aspecto importante de la física teórica y experimental; ^{[24] : 443} El concepto de Rutherford de una "sección transversal" ahora domina las descripciones de la física de partículas experimental. ^{[1] :  247} El historiador Silvan S. Schweber sugiere que el enfoque de Rutherford marcó el cambio a ver todas las interacciones y mediciones en física como procesos de dispersión. ^{[25] : xiv} Después de que el núcleo -un término que Rutherford introdujo en 1912 ^{[11] : 192} - se convirtiera en el modelo aceptado para el núcleo de los átomos, el análisis de Rutherford de la dispersión de partículas alfa creó una nueva rama de la física, la física nuclear. ^{[11] : 223}

El nuevo modelo atómico de Rutherford no causó revuelo. ^{[21] : 28} Rutherford ignora explícitamente los electrones, y sólo menciona el modelo saturniano de Hantaro Nagaoka de electrones orbitando un pequeño "sol", un modelo que había sido rechazado previamente por ser mecánicamente inestable. Al ignorar los electrones, Rutherford también ignora cualquier implicación potencial para la espectroscopia atómica en la química. ^{[11] : 302} El propio Rutherford no insistió en la defensa de su modelo atómico: su propio libro de 1913 sobre "Sustancias radiactivas y sus radiaciones" sólo menciona el átomo dos veces; otros libros de otros autores de la misma época se centran en el modelo de Thomson. ^{[26] : 446}

El impacto del modelo nuclear de Rutherford llegó después de que Niels Bohr llegara como estudiante de posdoctorado a Manchester por invitación de Rutherford. Bohr abandonó su trabajo sobre el modelo de Thomson en favor del modelo nuclear de Rutherford, desarrollando el modelo de Rutherford-Bohr durante los siguientes años. Finalmente, Bohr incorporó las primeras ideas de la mecánica cuántica al modelo del átomo, lo que permitió la predicción de espectros electrónicos y conceptos de química. ^{[8] : 304}

Hantaro Nagaoka , que había propuesto un modelo saturniano del átomo, escribió a Rutherford desde Tokio en 1911: "Me ha sorprendido la sencillez del aparato que emplea y los brillantes resultados que obtiene". ^[27] El astrónomo Arthur Eddington calificó el descubrimiento de Rutherford como el logro científico más importante desde que Demócrito propuso el átomo siglos antes. ^[28] Desde entonces, Rutherford ha sido aclamado como "el padre de la física nuclear". ^{[29] [30]}

En una conferencia pronunciada el 15 de octubre de 1936 en la Universidad de Cambridge, ^{[31] [32]} Rutherford describió su sorpresa por los resultados del experimento de 1909:

Recuerdo que dos o tres días después Geiger vino a verme muy emocionado y me dijo: "Hemos conseguido que algunas de las partículas α se desplacen hacia atrás...". Fue el acontecimiento más increíble que me ha ocurrido en mi vida. Era casi tan increíble como si hubieras disparado un proyectil de 15 pulgadas contra un trozo de papel de seda y éste te hubiera dado de vuelta. Tras pensarlo, me di cuenta de que esa dispersión hacia atrás debía ser el resultado de una única colisión, y cuando hice los cálculos vi que era imposible conseguir nada de ese orden de magnitud a menos que tomaras un sistema en el que la mayor parte de la masa del átomo estuviera concentrada en un núcleo diminuto. Fue entonces cuando se me ocurrió la idea de un átomo con un centro diminuto y masivo, que lleva una carga. ^[33]

La afirmación de Rutherford sobre la sorpresa es una buena historia, pero en el momento del experimento Geiger-Marsden el resultado confirmó las sospechas que Rutherford había desarrollado a partir de sus muchos experimentos anteriores. ^{[8] : 265}

Los primeros pasos de Rutherford hacia su descubrimiento de la naturaleza del átomo vinieron de su trabajo para entender las partículas alfa. ^{[21] : 17  [34] : 435} En 1906, Rutherford notó que las partículas alfa que pasaban a través de láminas de mica eran desviadas por las láminas hasta en 2 grados. Rutherford colocó una fuente radiactiva en un tubo sellado que terminaba con una ranura estrecha seguida de una placa fotográfica. La mitad de la ranura estaba cubierta por una fina capa de mica. Un campo magnético alrededor del tubo se alteraba cada 10 minutos para rechazar el efecto de los rayos beta, conocidos por ser sensibles a los campos magnéticos. ^[22] El tubo se evacuó a diferentes cantidades y se registró una serie de imágenes. A la presión más baja, la imagen de la ranura abierta era clara, mientras que las imágenes de la ranura cubierta de mica o la ranura abierta a presiones más altas eran borrosas. Rutherford explicó estos resultados como dispersión de partículas alfa ^{[8] : 260} en un artículo publicado en 1906. ^[35] Ya comprendía las implicaciones de la observación para los modelos de átomos: "tal resultado pone de manifiesto claramente el hecho de que los átomos de la materia deben ser la sede de fuerzas eléctricas muy intensas". ^{[35] : 145  [21]}

En un artículo de 1908 de Geiger, On the Scattering of α-Particles by Matter (Sobre la dispersión de partículas alfa por la materia ), se describe el siguiente experimento. Geiger construyó un tubo de vidrio largo, de casi dos metros de largo. En un extremo del tubo había una cantidad de " emanación de radio " (R) como fuente de partículas alfa. ^{[21] : 20} El extremo opuesto del tubo estaba cubierto con una pantalla fosforescente (Z). En el medio del tubo había una rendija de 0,9 mm de ancho. Las partículas alfa de R pasaban a través de la rendija y creaban una mancha de luz brillante en la pantalla. Se utilizó un microscopio (M) para contar los centelleos en la pantalla y medir su propagación. Geiger bombeó todo el aire fuera del tubo para que las partículas alfa no estuvieran obstruidas y dejaran una imagen nítida y ajustada en la pantalla que correspondía a la forma de la rendija. A continuación, Geiger dejó entrar algo de aire en el tubo y la mancha brillante se volvió más difusa. Geiger luego bombeó el aire y colocó una o dos láminas de oro sobre la ranura en AA. Esto también hizo que el parche de luz en la pantalla se extendiera más, con una dispersión mayor para dos capas. ^{[21] : 20} Este experimento demostró que tanto el aire como la materia sólida podían dispersar notablemente las partículas alfa. ^{[36] [21] : 20}

Los resultados de los experimentos iniciales de dispersión de partículas alfa fueron confusos. La dispersión angular de la partícula en la pantalla variaba mucho con la forma del aparato y su presión interna. Rutherford sugirió que Ernest Marsden, un estudiante de física de licenciatura que estudiaba con Geiger, debería buscar partículas alfa reflejadas de forma difusa o retrodispersadas, aunque no se esperaban. El primer reflector rudimentario de Marsden obtuvo resultados, por lo que Geiger lo ayudó a crear un aparato más sofisticado. Pudieron demostrar que 1 de cada 8000 colisiones de partículas alfa eran reflexiones difusas. ^{[21] : 23} Aunque esta fracción era pequeña, era mucho mayor de lo que el modelo de Thomson del átomo podía explicar. ^{[8] : 264}

Estos resultados se publicaron en un artículo de 1909, On a Diffuse Reflection of the α-Particles (Sobre la reflexión difusa de las partículas alfa ) , ^[37] donde Geiger y Marsden describieron el experimento con el que demostraron que las partículas alfa pueden dispersarse en más de 90°. En su experimento, prepararon un pequeño tubo de vidrio cónico (AB) que contenía "emanación de radio" ( radón ), "radio A" (radio real) y "radio C" ( bismuto -214); su extremo abierto estaba sellado con mica . Este era su emisor de partículas alfa. Luego instalaron una placa de plomo (P), detrás de la cual colocaron una pantalla fluorescente (S). El tubo se sostuvo en el lado opuesto de la placa, de modo que las partículas alfa que emitía no pudieran golpear directamente la pantalla. Notaron algunas centelleos en la pantalla porque algunas partículas alfa rodeaban la placa rebotando en las moléculas de aire. Luego colocaron una lámina de metal (R) al costado de la placa de plomo. Hicieron pruebas con plomo, oro, estaño, aluminio, cobre, plata, hierro y platino. Dirigieron el tubo hacia la lámina para ver si las partículas alfa rebotaban en ella y golpeaban la pantalla del otro lado de la placa, y observaron un aumento en el número de centelleos en la pantalla. Al contar los centelleos, observaron que los metales con mayor masa atómica, como el oro, reflejaban más partículas alfa que los más ligeros, como el aluminio. ^{[37] [21] : 20}

Geiger y Marsden querían entonces estimar el número total de partículas alfa que se reflejaban. La configuración anterior no era adecuada para hacer esto porque el tubo contenía varias sustancias radiactivas (radio más sus productos de desintegración) y, por lo tanto, las partículas alfa emitidas tenían rangos variables , y porque era difícil para ellos determinar a qué velocidad el tubo emitía partículas alfa. Esta vez, colocaron una pequeña cantidad de radio C (bismuto-214) en la placa de plomo, que rebotó en un reflector de platino (R) y en la pantalla. Llegaron a la conclusión de que aproximadamente 1 de cada 8.000 de las partículas alfa que golpeaban el reflector rebotaban en la pantalla. ^[37] Al medir la reflexión de láminas delgadas, demostraron que el efecto se debía a un efecto de volumen y no de superficie. ^[22] Cuando se contrastaba con la gran cantidad de partículas alfa que pasan sin obstáculos a través de una lámina de metal, esta pequeña cantidad de reflexiones de ángulo grande era un resultado extraño ^{[1] : 240} que significaba que estaban involucradas fuerzas muy grandes. ^[22]

En un artículo de 1910 ^[38] de Geiger, The Scattering of the α-Particles by Matter (La dispersión de las partículas alfa por la materia ), se describe un experimento para medir cómo varía el ángulo más probable a través del cual se desvía una partícula alfa con el material que atraviesa, el espesor del material y la velocidad de las partículas alfa. Geiger construyó un tubo de vidrio hermético del que se bombeaba el aire. En un extremo había una bombilla (B) que contenía "emanación de radio" ( radón -222). Por medio de mercurio, el radón en B se bombeaba hacia arriba por el estrecho tubo de vidrio cuyo extremo en A estaba tapado con mica . En el otro extremo del tubo había una pantalla fluorescente de sulfuro de zinc (S). El microscopio que utilizó para contar los centelleos en la pantalla estaba fijado a una escala milimétrica vertical con un vernier, lo que permitió a Geiger medir con precisión dónde aparecían los destellos de luz en la pantalla y así calcular los ángulos de desviación de las partículas. Las partículas alfa emitidas desde A se redujeron a un haz mediante un pequeño orificio circular en D. Geiger colocó una lámina metálica en el camino de los rayos en D y E para observar cómo cambiaba la zona de destellos. Probó con oro, estaño, plata, cobre y aluminio. También pudo variar la velocidad de las partículas alfa colocando láminas adicionales de mica o aluminio en A. ^[38]

A partir de las mediciones que tomó, Geiger llegó a las siguientes conclusiones: ^{[17] : 5}

• El ángulo de desviación más probable aumenta con el espesor del material.
• El ángulo de desviación más probable es proporcional a la masa atómica de la sustancia.
• El ángulo de desviación más probable disminuye con la velocidad de las partículas alfa.

Teniendo en cuenta los resultados de estos experimentos, Rutherford publicó un artículo de referencia en 1911 titulado "La dispersión de partículas α y β por la materia y la estructura del átomo", en el que demostró que la dispersión simple de una carga eléctrica muy pequeña e intensa predice principalmente una dispersión de ángulo pequeño con cantidades pequeñas pero mensurables de retrodispersión. ^{[1] : 252  [39]} Para el propósito de sus cálculos matemáticos, asumió que esta carga central era positiva, pero admitió que no podía probarlo y que tenía que esperar otros experimentos para desarrollar su teoría. ^{[39] : 688}

Rutherford desarrolló una ecuación matemática que modelaba cómo la lámina debería dispersar las partículas alfa si toda la carga positiva y la mayor parte de la masa atómica se concentraran en un punto en el centro de un átomo. A partir de los datos de dispersión, Rutherford estimó que la carga central q _n era de aproximadamente +100 unidades. ^[40]

El artículo de Rutherford no analiza ninguna disposición de electrones más allá de las discusiones sobre la dispersión del modelo de pudín de pasas de Thomson y el modelo saturniano de Nagaoka. ^{[8] : 303} Muestra que los resultados de dispersión predichos por el modelo de Thomson también se explican por la dispersión simple, pero que el modelo de Thomson no explica la dispersión de ángulo grande. Dice que el modelo de Nagaoka, al tener una carga compacta, estaría de acuerdo con los datos de dispersión. El modelo saturniano había sido rechazado previamente por otros motivos. El llamado modelo de Rutherford del átomo con electrones en órbita no fue propuesto por Rutherford en el artículo de 1911. ^{[8] : 304}

En un artículo de 1913, The Laws of Deflexion of α Particles through Large Angles (Las leyes de la deflexión de partículas α a través de ángulos grandes) , ^[41] Geiger y Marsden describen una serie de experimentos con los que intentaron verificar experimentalmente la ecuación de Rutherford. La ecuación de Rutherford predijo que la cantidad de centelleos por minuto s que se observarán en un ángulo dado Φ debería ser proporcional a: ^{[17] : 11}

1. cosec ⁴ ⁠Φ/2⁠
2. espesor de la lámina t
3. magnitud del cuadrado de la carga central Q _n
4. ⁠1/( mv2 ^{) 2}​⁠

Su artículo de 1913 describe cuatro experimentos mediante los cuales demostraron cada una de estas cuatro relaciones. ^{[24] : 438}

Para probar cómo variaba la dispersión con el ángulo de desviación (es decir, si s ∝ csc ⁴ ⁠Φ/2⁠ ). Geiger y Marsden construyeron un aparato que consistía en un cilindro hueco de metal montado sobre una plataforma giratoria. Dentro del cilindro había una lámina metálica (F) y una fuente de radiación que contenía radón (R), montada sobre una columna separada (T) que permitía que el cilindro girara de forma independiente. La columna también era un tubo por el que se bombeaba aire fuera del cilindro. Un microscopio (M) con su lente objetivo cubierta por una pantalla fluorescente de sulfuro de zinc (S) penetraba la pared del cilindro y apuntaba a la lámina metálica. Probaron con láminas de plata y oro. Al girar la plataforma, el microscopio podía moverse un círculo completo alrededor de la lámina, lo que permitía a Geiger observar y contar partículas alfa desviadas hasta 150°. Al corregir el error experimental, Geiger y Marsden descubrieron que la cantidad de partículas alfa que se desvían en un ángulo dado Φ es de hecho proporcional a csc ⁴ ⁠Φ/2⁠ . ^[41]

Geiger y Marsden probaron entonces cómo variaba la dispersión con el espesor de la lámina (es decir, si s ∝ t ). Construyeron un disco (S) con seis agujeros perforados en él. Los agujeros se cubrieron con una lámina metálica (F) de espesor variable, o ninguna para el control. Luego, este disco se selló en un anillo de latón (A) entre dos placas de vidrio (B y C). El disco se podía girar por medio de una varilla (P) para poner cada ventana frente a la fuente de partículas alfa (R). En el panel de vidrio trasero había una pantalla de sulfuro de zinc (Z). Geiger y Marsden descubrieron que la cantidad de centelleos que aparecían en la pantalla era de hecho proporcional al espesor, siempre que este fuera pequeño. ^[41]

Geiger y Marsden reutilizaron el aparato para medir cómo variaba el patrón de dispersión con el cuadrado de la carga nuclear (es decir, si s ∝ Q _n ² ). Geiger y Marsden no sabían cuál era la carga positiva del núcleo de sus metales (apenas habían descubierto que el núcleo existía), pero asumieron que era proporcional al peso atómico, por lo que probaron si la dispersión era proporcional al peso atómico al cuadrado. Geiger y Marsden cubrieron los agujeros del disco con láminas de oro, estaño, plata, cobre y aluminio. Midieron el poder de frenado de cada lámina comparándola con un espesor equivalente de aire. Contaron el número de centelleos por minuto que cada lámina producía en la pantalla. Dividieron el número de centelleos por minuto por el equivalente en aire de la respectiva lámina, y luego dividieron nuevamente por la raíz cuadrada del peso atómico (Geiger y Marsden sabían que para láminas con igual poder de frenado, el número de átomos por unidad de área es proporcional a la raíz cuadrada del peso atómico). De esta manera, para cada metal, Geiger y Marsden obtuvieron el número de centelleos que produce un número fijo de átomos. Para cada metal, luego dividieron este número por el cuadrado del peso atómico y descubrieron que las proporciones eran aproximadamente las mismas. De esta manera, probaron que s ∝ Q _n ² . ^[41]

Finalmente, Geiger y Marsden probaron cómo variaba la dispersión con la velocidad de las partículas alfa (es decir, si s ∝ ⁠1/versión ⁴⁠ ). Utilizando el mismo aparato, ralentizaron las partículas alfa colocando láminas adicionales de mica delante de la fuente de partículas alfa. Descubrieron que, dentro del rango de error experimental, el número de centelleos era efectivamente proporcional a ⁠1/versión ⁴⁠ . ^[41]

En su artículo de 1911 (ver arriba), Rutherford asumió que la carga central del átomo era positiva, pero una carga negativa habría encajado igualmente bien en su modelo de dispersión. ^[42] En un artículo de 1913, Rutherford declaró que el "núcleo" (como lo llamó ahora) estaba efectivamente cargado positivamente, basándose en el resultado de experimentos que exploraban la dispersión de partículas alfa en varios gases. ^[43]

En 1917, Rutherford y su asistente William Kay comenzaron a explorar el paso de partículas alfa a través de gases como el hidrógeno y el nitrógeno. En este experimento, lanzaron un haz de partículas alfa a través del hidrógeno y colocaron cuidadosamente su detector (una pantalla de sulfuro de cinc) justo fuera del alcance de las partículas alfa, que fueron absorbidas por el gas. No obstante, detectaron partículas cargadas de algún tipo que causaron centelleos en la pantalla. Rutherford interpretó esto como partículas alfa que golpeaban los núcleos de hidrógeno hacia adelante en la dirección del haz, no hacia atrás. ^[42]

Rutherford comienza su artículo de 1911 ^[39] con una discusión de los resultados de Thomson sobre la dispersión de partículas beta , una forma de radiactividad que produce electrones de alta velocidad. El modelo de Thomson tenía electrones circulando dentro de una esfera de carga positiva. Rutherford destaca la necesidad de eventos de dispersión compuestos o múltiples: las desviaciones predichas para cada colisión son mucho menores a un grado. Luego propone un modelo que producirá grandes desviaciones en un solo encuentro: coloca toda la carga positiva en el centro de la esfera e ignora la dispersión de electrones como insignificante. La carga concentrada explicará por qué la mayoría de las partículas alfa no se dispersan en absoluto (no alcanzan la carga en absoluto) y, sin embargo, las partículas que golpean el centro se dispersan a través de grandes ángulos. ^{[8] : 285}

Rutherford comienza su análisis considerando una colisión frontal entre la partícula alfa y el átomo. Esto establecerá la distancia mínima entre ellos, un valor que será utilizado en todos sus cálculos. ^{[39] : 670}

Suponiendo que no hay fuerzas externas y que inicialmente las partículas alfa están lejos del núcleo, la ley del cuadrado inverso entre las cargas de la partícula alfa y el núcleo da la energía potencial que gana la partícula a medida que se acerca al núcleo. En caso de colisiones frontales entre partículas alfa y el núcleo, toda la energía cinética de la partícula alfa se convierte en energía potencial y la partícula se detiene y da marcha atrás. ^{[17] : 5}

Cuando la partícula se detiene a cierta distancia del centro, la energía potencial coincide con la energía cinética original: ^{[44] : 620  [45] : 320}${\displaystyle r_{\text{min}}}$

$${\displaystyle {\frac {1}{2}}mv^{2}=k{\frac {q_{a}q_{g}}{r_{\text{min}}}}}$$

dónde

$${\displaystyle k={\frac {1}{4\pi \epsilon _{0}}}}$$

Reordenando: ^{[39] :  671} $${\displaystyle r_{\text{min}}=k{\frac {2q_{a}q_{g}}{mv^{2}}}}$$

Para una partícula alfa:

• m (masa) =6.644 24 × 10 ⁻²⁷  kg =3,7273 × 10 ^{9 eV}  / c2
• q _a (para la partícula alfa) = 2 ×1,6 × 10 ⁻¹⁹  C =3,2 × 10 ⁻¹⁹  C
• q _g (para oro) = 79 ×1,6 × 10 ⁻¹⁹  C =1,27 × 10 ⁻¹⁷  C
• v (velocidad inicial) =2 × 10 ⁷  m/s (para este ejemplo)

La distancia desde la partícula alfa hasta el centro del núcleo ( r _min ) en este punto es un límite superior para el radio nuclear. Sustituyéndolos en obtenemos el valor de aproximadamente2,7 × 10 ⁻¹⁴  m , o 27  fm . (El radio real es de aproximadamente 7,3 fm). El radio real del núcleo no se recupera en estos experimentos porque los alfas no tienen suficiente energía para penetrar a más de 27 fm del centro nuclear, como se señaló, cuando el radio real del oro es de 7,3 fm.

El artículo de Rutherford de 1911 ^[39] comenzaba con una fórmula ligeramente diferente, adecuada para una colisión frontal con una esfera de carga positiva:

$${\displaystyle {\frac {1}{2}}mv^{2}=NeE\cdot \left({\frac {1}{b}}-{\frac {3}{2R}}+{\frac {b^{2}}{2R^{3}}}\right)}$$

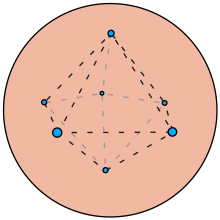
En la notación de Rutherford, e es la carga elemental , N es el número de carga del núcleo (ahora sabemos que es igual al número atómico) y E es la carga de una partícula alfa. La convención en la época de Rutherford era medir la carga en unidades electrostáticas , la distancia en centímetros, la fuerza en dinas y la energía en ergios . La convención moderna es medir la carga en culombios , la distancia en metros, la fuerza en newtons y la energía en julios . El uso de culombios requiere el uso de la constante de Coulomb ( k ) en la ecuación. Rutherford usó b como la distancia del punto de inflexión (llamada r _min arriba) y R es el radio del átomo. El primer término es la repulsión de Coulomb utilizada anteriormente. Esta forma supone que la partícula alfa podría penetrar la carga positiva. En el momento del artículo de Rutherford, el modelo de pudín de pasas de Thomson proponía una carga positiva con el radio de un átomo, miles de veces más grande que el r _min encontrado anteriormente. La figura 1 muestra cuán concentrado está este potencial en comparación con el tamaño del átomo. Muchos de los resultados de Rutherford se expresan en términos de esta distancia del punto de inflexión r _min , lo que simplifica los resultados y limita la necesidad de unidades para este cálculo del punto de inflexión.

A partir de sus resultados para una colisión frontal, Rutherford sabe que la dispersión de partículas alfa ocurre cerca del centro de un átomo, en un radio 10.000 veces más pequeño que el átomo. Los electrones tienen un efecto insignificante. Comienza asumiendo que no hay pérdida de energía en la colisión, es decir, ignora el retroceso del átomo objetivo. Volverá a tratar cada uno de estos temas más adelante en su artículo. ^{[39] : 672} Bajo estas condiciones, la partícula alfa y el átomo interactúan a través de una fuerza central , un problema físico estudiado por primera vez por Isaac Newton . ^[46] Una fuerza central solo actúa a lo largo de una línea entre las partículas y cuando la fuerza varía con el cuadrado inverso, como la fuerza de Coulomb en este caso, se desarrolló una teoría detallada bajo el nombre de problema de Kepler . ^{[47] : 76} Las soluciones bien conocidas al problema de Kepler se llaman órbitas y las órbitas no ligadas son hipérbolas . Así, Rutherford propuso que la partícula alfa tomará una trayectoria hiperbólica en la fuerza repulsiva cerca del centro del átomo como se muestra en la Figura 2.

Para aplicar las soluciones de la trayectoria hiperbólica al problema de la partícula alfa, Rutherford expresa los parámetros de la hipérbola en términos de la geometría de dispersión y las energías. Comienza con la conservación del momento angular . Cuando la partícula de masa y velocidad inicial está lejos del átomo, su momento angular alrededor del centro del átomo será donde es el parámetro de impacto , que es la distancia lateral entre la trayectoria de la partícula alfa y el átomo. En el punto de aproximación más cercano, etiquetado A en la Figura 2, el momento angular será . Por lo tanto ^{[8] : 270}${\displaystyle m}$${\displaystyle v_{0}}$${\displaystyle mbv_{0}}$${\displaystyle b}$${\displaystyle mr_{A}v_{A}}$

$${\displaystyle mbv_{0}=mr_{A}v_{A}}$$

$${\displaystyle v_{A}={\frac {bv_{0}}{r_{A}}}}$$

Rutherford también aplica la ley de conservación de la energía entre los mismos dos puntos:

$${\displaystyle {\tfrac {1}{2}}mv_{0}^{2}={\tfrac {1}{2}}mv_{A}^{2}+{\frac {kq_{a}q_{g}}{r_{A}}}}$$

El lado izquierdo y el primer término del lado derecho son las energías cinéticas de la partícula en los dos puntos; el último término es la energía potencial debida a la fuerza de Coulomb entre la partícula alfa y el átomo en el punto de aproximación más cercana (A). q _a es la carga de la partícula alfa, q _g es la carga del núcleo y k es la constante de Coulomb . ^[48]

La ecuación de energía puede entonces reorganizarse de la siguiente manera:

$${\displaystyle v_{A}^{2}=v_{0}^{2}\left(1-{\frac {kq_{a}q_{g}}{{\tfrac {1}{2}}mv_{0}^{2}r_{A}}}\right)}$$

Para mayor comodidad, las variables físicas no geométricas en esta ecuación ^{[39] : 674} se pueden contener en una variable , que es el punto de aproximación más cercano en un escenario de colisión frontal ^{[39] :  671} que se exploró en una sección anterior de este artículo:${\displaystyle r_{\text{min}}}$

$${\displaystyle r_{\text{min}}={\frac {kq_{a}q_{g}}{{\tfrac {1}{2}}mv_{0}^{2}}}}$$

Esto permite a Rutherford simplificar la ecuación energética a:

$${\displaystyle v_{A}^{2}=v_{0}^{2}\left(1-{\frac {r_{\text{min}}}{r_{A}}}\right)}$$

Esto deja dos ecuaciones simultáneas para , la primera derivada de la ecuación de conservación del momento y la segunda de la ecuación de conservación de la energía. Al eliminar y se obtiene una nueva fórmula para :${\displaystyle v_{A}^{2}}$${\displaystyle v_{A}}$${\displaystyle v_{0}}$${\displaystyle r_{\text{min}}}$

$${\displaystyle v_{A}^{2}={\frac {b^{2}v_{0}^{2}}{r_{A}^{2}}}=v_{0}^{2}\left(1-{\frac {r_{\text{min}}}{r_{A}}}\right)}$$

$${\displaystyle r_{\text{min}}=r_{A}-{\frac {b^{2}}{r_{A}}}}$$

El siguiente paso es encontrar una fórmula para . De la Figura 2, es la suma de dos distancias relacionadas con la hipérbola, SO y OA. Usando la siguiente lógica, estas distancias pueden expresarse en términos de ángulo y parámetro de impacto .${\displaystyle r_{A}}$${\displaystyle r_{A}}$${\displaystyle \Phi }$${\displaystyle b}$

La excentricidad de una hipérbola es un valor que describe la forma de la hipérbola. Se puede calcular dividiendo la distancia focal por la longitud del semieje mayor, que según la Figura 2 esENTONCES/OA⁠ . Como se puede ver en la Figura 3, la excentricidad también es igual a${\displaystyle \sec \Phi }$ , donde es el ángulo entre el eje mayor y la asíntota. ^{[49] : 219} Por lo tanto:${\displaystyle \Phi }$

$${\displaystyle {\frac {\text{SO}}{\text{OA}}}=\sec \Phi }$$

Como se puede deducir de la Figura 2, la distancia focal SO es

$${\displaystyle {\text{SO}}=b\csc \Phi }$$

y por lo tanto

$${\displaystyle {\text{OA}}={\frac {\text{SO}}{\sec \Phi }}=b\cot \Phi }$$

Con estas fórmulas para SO y OA, ahora podemos encontrar una fórmula para . La distancia se puede escribir en términos de y simplificar utilizando una identidad trigonométrica conocida como fórmula de medio ángulo : ^{[40] : 673}${\displaystyle r_{A}}$${\displaystyle r_{A}}$${\displaystyle \Phi }$

$${\displaystyle r_{A}={\text{SO}}+{\text{OA}}}$$

$${\displaystyle =b\csc \Phi +b\cot \Phi }$$

$${\displaystyle =b\cot {\frac {\Phi }{2}}}$$

Usando la ecuación anterior, ahora podemos encontrar una relación más simple entre las variables físicas y geométricas con la ayuda de una identidad trigonométrica conocida como la fórmula del ángulo doble cotangente :${\displaystyle r_{A}}$

$${\displaystyle r_{\text{min}}=r_{A}-{\frac {b^{2}}{r_{A}}}}$$

$${\displaystyle =b\cot {\frac {\Phi }{2}}-{\frac {b^{2}}{b\cot {\frac {\Phi }{2}}}}}$$

$${\displaystyle =b{\frac {\cot ^{2}{\frac {\Phi }{2}}-1}{\cot {\frac {\Phi }{2}}}}}$$

$${\displaystyle =2b\cot \Phi }$$

El ángulo de dispersión de la partícula es y por lo tanto . Con la ayuda de una identidad trigonométrica conocida como fórmula de reflexión , la relación entre θ y b se puede resolver en: ^{[39] : 673}${\displaystyle \theta =\pi -2\Phi }$${\displaystyle \Phi ={\tfrac {\pi -\theta }{2}}}$

$${\displaystyle r_{\text{min}}=2b\cot \left({\frac {\pi -\theta }{2}}\right)}$$

$${\displaystyle =2b\tan {\frac {\theta }{2}}}$$

$${\displaystyle \cot {\frac {\theta }{2}}={\frac {2b}{r_{\text{min}}}}}$$

que se puede reorganizar para dar

$${\displaystyle \theta =2\arctan {\frac {r_{\text{min}}}{2b}}=2\arctan \left({\frac {kq_{a}q_{g}}{mv_{0}^{2}b}}\right)}$$

Rutherford da algunos valores ilustrativos como se muestra en esta tabla: ^{[39] : 673}

Tabla de ángulos de desviación de Rutherford

${\displaystyle b/r_{\text{min}}}$	10	5	2	1	0,5	0,25	0,125
${\displaystyle \theta }$	5,7°	11,4°	28°	53°	90°	127°	152°

El enfoque de Rutherford para este problema de dispersión sigue siendo un tratamiento estándar en los libros de texto ^{[50] : 151  [51] : 240  [52] :  400} sobre mecánica clásica .

Para comparar con los experimentos, la relación entre el parámetro de impacto y el ángulo de dispersión debe convertirse en probabilidad versus ángulo. La sección transversal de dispersión proporciona la intensidad relativa por ángulos: ^{[47] : 81}$${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}(\Omega )\mathrm {d} \Omega ={\frac {{\text{number of particles scattered into solid angle }}\mathrm {d} \Omega {\text{ per unit time}}}{\text{incident intensity}}}}$$

En mecánica clásica, el ángulo de dispersión está determinado únicamente por la energía cinética inicial de las partículas entrantes y el parámetro de impacto b . ^{[47] : 82} Por lo tanto, el número de partículas dispersadas en un ángulo entre y debe ser el mismo que el número de partículas con parámetros de impacto asociados entre b y b + db . Para una intensidad incidente I , esto implica: Por lo tanto, la sección transversal depende del ángulo de dispersión como: Usando el parámetro de impacto como una función del ángulo, b ( θ ) , a partir del resultado de dispersión simple anterior se produce la sección transversal de dispersión de Rutherford: ^{[47] : 84}${\displaystyle \theta }$${\displaystyle \theta }$${\displaystyle \theta +\mathrm {d} \theta }$$${\displaystyle 2\pi Ib\left|\mathrm {d} b\right|=-2\pi \sigma (\theta )I\sin(\theta )\mathrm {d} \theta }$$$${\displaystyle \sigma (\theta )=-{\frac {b}{\sin \theta }}{\frac {\mathrm {d} b}{\mathrm {d} \theta }}}$$

$${\displaystyle s={\frac {Xnt\cdot \csc ^{4}{\frac {\phi }{2}}}{16r^{2}}}\cdot {\left({\frac {2kq_{n}q_{a}}{mv^{2}}}\right)}^{2}}$$

• s = el número de partículas alfa que caen sobre una unidad de área en un ángulo de desviación Φ
• r = distancia desde el punto de incidencia de los rayos α sobre el material dispersante
• X = número total de partículas que caen sobre el material dispersante
• n = número de átomos en una unidad de volumen del material
• t = espesor de la lámina
• q _n = carga positiva del núcleo atómico
• q _a = carga positiva de las partículas alfa
• m = masa de una partícula alfa
• v = velocidad de la partícula alfa

Esta fórmula predijo los resultados que Geiger midió el año siguiente. La probabilidad de dispersión en ángulos pequeños supera con creces la probabilidad en ángulos mayores, lo que refleja el diminuto núcleo rodeado de espacio vacío. Sin embargo, en los raros encuentros cercanos, la dispersión en ángulos grandes se produce con un solo objetivo. ^{[53] : 19}

Al final de su desarrollo de la fórmula de la sección transversal, Rutherford enfatiza que los resultados se aplican a la dispersión simple y, por lo tanto, requieren mediciones con láminas delgadas. Para láminas delgadas, el grado de dispersión es proporcional al espesor de la lámina, de acuerdo con las mediciones de Geiger. ^[39]

En el momento del artículo de Rutherford, JJ Thomson era el "maestro mundial indiscutible en el diseño de átomos". ^{[8] : 296} Rutherford necesitaba comparar su nuevo enfoque con el de Thomson. El modelo de Thomson, presentado en 1910, ^[18] modelaba las colisiones de electrones con órbitas hiperbólicas de su artículo de 1906 ^[54] combinadas con un factor para la esfera positiva. Las pequeñas desviaciones resultantes múltiples se combinaron utilizando un paseo aleatorio . ^{[8] : 277}

En su artículo, Rutherford enfatizó que la dispersión simple por sí sola podría explicar los resultados de Thomson si la carga positiva estuviera concentrada en el centro. Rutherford calcula la probabilidad de dispersión simple a partir de una carga compacta y demuestra que es tres veces mayor que la probabilidad de dispersión múltiple de Thomson. Rutherford completa su análisis incluyendo los efectos de la densidad y el espesor de la lámina, luego concluye que las láminas delgadas están regidas por la dispersión simple, no por la dispersión múltiple. ^{[8] : 298}

Un análisis posterior demostró que el modelo de dispersión de Thomson no podía explicar la dispersión grande. La desviación angular máxima de la dispersión de electrones o de la esfera positiva es menor de 0,02°; incluso muchos de estos eventos de dispersión combinados darían como resultado una desviación promedio menor de un grado y una probabilidad de dispersión a través de 90° de menos de una en 10 ³⁵⁰⁰ . ^{[55] : 106}

El análisis de Rutherford suponía que las trayectorias de las partículas alfa giraban en el centro del átomo, pero que la velocidad de salida no se reducía. ^{[1] : 253} Esto equivale a suponer que la carga concentrada en el centro tenía una masa infinita o estaba anclada en un lugar. Rutherford analiza las limitaciones de esta suposición comparando la dispersión de átomos más ligeros, como el aluminio, con átomos más pesados, como el oro. Si la carga concentrada es más ligera, retrocederá ante la interacción, ganando impulso, mientras que la partícula alfa pierde impulso y, en consecuencia, se ralentiza. ^{[40] :  676}

Los tratamientos modernos analizan este tipo de dispersión de Coulomb en el marco de referencia del centro de masas . Las seis coordenadas de las dos partículas (también llamadas "cuerpos") se convierten en tres coordenadas relativas entre las dos partículas y tres coordenadas del centro de masas que se mueven en el espacio (llamado marco de laboratorio). La interacción solo ocurre en las coordenadas relativas, lo que da como resultado un problema de un cuerpo equivalente ^{[47] : 58} tal como lo resolvió Rutherford, pero con diferentes interpretaciones para la masa y el ángulo de dispersión.

En lugar de la masa de la partícula alfa, la fórmula más precisa que incluye el retroceso utiliza una masa reducida : ^{[47] : 80} Para la dispersión de partículas alfa de Rutherford a partir del oro, con una masa de 197, la masa reducida es muy cercana a la masa de la partícula alfa: Para el aluminio más ligero, con una masa de 27, el efecto es mayor: una diferencia del 13% en la masa. Rutherford nota esta diferencia y sugiere que se realicen experimentos con átomos más ligeros. ^{[39] : 677}$${\displaystyle \mu ={\cfrac {m_{1}m_{2}}{m_{1}+m_{2}}}.}$$$${\displaystyle \mu _{\text{Au}}={\cfrac {4\times 197}{4+197}}=3.92\approx 4}$$$${\displaystyle \mu _{\text{Au}}={\cfrac {4\times 27}{4+27}}=3.48}$$

El segundo efecto es un cambio en el ángulo de dispersión. El ángulo en el sistema de coordenadas relativas o el marco del centro de masa debe convertirse en un ángulo en el marco de laboratorio. ^{[47] : 85} En el marco de laboratorio, denotado por un subíndice L, el ángulo de dispersión para un potencial central general es Para una partícula pesada como el oro utilizado por Rutherford, y en casi todos los ángulos podemos descuidar este factor: los ángulos de laboratorio y relativos son los mismos, . $${\displaystyle \tan \Theta _{L}={\frac {\sin \Theta }{\cos \Theta +(m_{1}/m_{2})}}}$$${\displaystyle m_{1}/m_{2}=4/197\approx 0.02\ll 1}$${\displaystyle \Theta _{L}\approx \Theta }$

El cambio en el ángulo de dispersión altera la fórmula para la sección transversal diferencial necesaria para la comparación con el experimento. Para cualquier potencial central, la sección transversal diferencial en el marco de laboratorio está relacionada con la del marco del centro de masas por ^{[47] : 88} donde$${\displaystyle {\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}_{L}={\frac {\left(1+2s\cos \Theta +s^{2}\right)^{3/2}}{1+s\cos \Theta }}{\frac {\mathrm {d} \sigma }{\mathrm {d} \Omega }}}$$${\displaystyle s=m_{1}/m_{2}}$

En 1919, Rutherford analizó la dispersión de partículas alfa de los átomos de hidrógeno, ^[56] mostrando los límites de la fórmula de 1911 incluso con correcciones para la masa reducida. ^{[57] : 191} Problemas similares con desviaciones más pequeñas para He, Mg y Al ^[58] llevaron a la conclusión de que la partícula alfa estaba penetrando el núcleo en estos casos. Esto permitió las primeras estimaciones del tamaño de los núcleos atómicos. ^{[1] : 255} Experimentos posteriores basados ​​en la aceleración ciclotrónica de partículas alfa que golpeaban núcleos más pesados ​​proporcionaron datos para el análisis de la interacción entre la partícula alfa y la superficie nuclear. Sin embargo, a energías que empujan las partículas alfa más profundamente, son fuertemente absorbidas por los núcleos, una interacción más compleja. ^{[57] : 228  [24] : 441}

El tratamiento de Rutherford de la dispersión de partículas alfa parece basarse en la mecánica clásica y, sin embargo, las partículas son de dimensiones subatómicas. Sin embargo, los aspectos críticos de la teoría dependen en última instancia de la conservación del momento y la energía. Estos conceptos se aplican por igual en regímenes clásicos y cuánticos: las ideas de dispersión desarrolladas por Rutherford se aplican a problemas de dispersión elástica subatómica como la dispersión neutrón-protón. ^{[47] : 89}

Esta sección presenta un método alternativo para encontrar la relación entre el parámetro de impacto y el ángulo de deflexión en un encuentro de un solo átomo, utilizando un enfoque centrado en la fuerza en oposición al centrado en la energía que utilizó Rutherford.

La geometría de dispersión se muestra en este diagrama ^{[59] [55] : 106}

El parámetro de impacto b es la distancia entre la trayectoria inicial de la partícula alfa y una línea paralela que pasa por el núcleo. Los valores más pequeños de b acercan la partícula al átomo, por lo que siente más fuerza de desviación, lo que da como resultado un ángulo de desviación θ mayor . ^{[47] : 82} El objetivo es encontrar la relación entre b y el ángulo de desviación.

La trayectoria de la partícula alfa es una hipérbola y el cambio neto en el momento se desarrolla a lo largo del eje de simetría. A partir de la geometría del diagrama y de la magnitud de los vectores de momento inicial y final, , la magnitud de se puede relacionar con el ángulo de deflexión: ^{[55] : 111}${\displaystyle \Delta {\vec {P}}}$${\displaystyle |{\vec {P}}_{i}|=|{\vec {P}}_{f}|=mv}$${\displaystyle \Delta {\vec {P}}}$

$${\displaystyle \Delta P=2mv\cdot \sin {\frac {\theta }{2}}.}$$

Una segunda fórmula para involucrar b dará la relación con el ángulo de deflexión. El cambio neto en el momento también se puede encontrar sumando pequeños incrementos al momento a lo largo de la trayectoria utilizando la integral${\displaystyle \Delta P}$

$${\displaystyle \Delta P=\int \limits _{0}^{\infty }{\frac {kq_{a}q_{g}}{r^{2}}}\cdot \cos \varphi \cdot \mathrm {\mathrm {d} } t}$$

donde es la distancia entre la partícula alfa y el centro del núcleo y es su ángulo desde el eje de simetría. Estas dos son las coordenadas polares de la partícula alfa en el tiempo . Aquí la fuerza de Coulomb ejercida a lo largo de la línea entre la partícula alfa y el átomo es y el factor da la parte de la fuerza que causa la desviación. ${\displaystyle r}$${\displaystyle \varphi }$${\displaystyle t}$${\displaystyle {\frac {kq_{a}q_{g}}{r^{2}}}}$${\displaystyle \cos \varphi }$

Las coordenadas polares r y φ dependen de t en la integral, pero deben estar relacionadas entre sí, ya que ambas varían a medida que la partícula se mueve. Al cambiar la variable y los límites de integración de t a φ, esta conexión queda explícita: ^{[55] : 112}

$${\displaystyle \Delta P=\int \limits _{-{\frac {\pi -\theta }{2}}}^{\frac {\pi -\theta }{2}}{\frac {kq_{a}q_{g}}{r^{2}}}\cdot \cos \varphi \cdot {\frac {\mathrm {d} t}{\mathrm {d} \varphi }}\cdot \mathrm {d} \varphi }$$

El factor es el recíproco de la velocidad angular de la partícula. Como la fuerza sólo se ejerce a lo largo de la línea entre la partícula y el átomo, el momento angular , que es proporcional a la velocidad angular, es constante: Esta ley de conservación del momento angular proporciona una fórmula para :${\displaystyle \mathrm {d} t/\mathrm {d} \varphi =1/\omega }$$${\displaystyle mvb=mr^{2}\omega =mr^{2}{\frac {\mathrm {d} \varphi }{\mathrm {d} t}}}$$${\displaystyle \mathrm {d} t/\mathrm {d} \varphi }$

$${\displaystyle {\frac {\mathrm {d} t}{\mathrm {d} \varphi }}={\frac {r^{2}}{vb}}}$$

Reemplazando en la integral por Δ P se elimina simultáneamente la dependencia de r :${\displaystyle \mathrm {d} t/\mathrm {d} \varphi }$

$${\displaystyle \Delta P=\int \limits _{-{\frac {\pi -\theta }{2}}}^{\frac {\pi -\theta }{2}}{\frac {kq_{a}q_{g}}{vb}}\cdot \cos \varphi \cdot \mathrm {d} \varphi }$$

$${\displaystyle ={\frac {kq_{a}q_{g}}{vb}}\left(\sin \left[{\frac {\pi -\theta }{2}}\right]-\sin \left[-{\frac {\pi -\theta }{2}}\right]\right)}$$

Aplicando las identidades trigonométricas y simplificando este resultado se obtiene la segunda fórmula para :${\displaystyle \sin({\tfrac {\pi }{2}}-\theta )=\cos \theta }$${\displaystyle \sin(\theta \pm {\tfrac {\pi }{2}})=\pm \cos \theta }$${\displaystyle \Delta P}$

$${\displaystyle \Delta P={\frac {kq_{a}q_{g}}{vb}}\cdot 2\cos {\frac {\theta }{2}}=2mv\cdot \sin {\frac {\theta }{2}}}$$Resolviendo θ como función de b obtenemos el resultado final

$${\displaystyle \theta =2\arctan \left({\frac {kq_{a}q_{g}}{mv^{2}b}}\right)}$$

Ahora podemos estimar algunos valores para θ en relación con b utilizando los siguientes valores:

• q _g = carga positiva del átomo de oro =79  y =1,26 × 10 ⁻¹⁷  C
• q _a = carga de la partícula alfa =2  y =3,20 × 10 ⁻¹⁹  C
• v = velocidad de la partícula alfa =1,53 × 10 ⁷  m/s
• m = masa de la partícula alfa =6,64 × 10 ⁻²⁷  kg
• k = constante de Coulomb =8,987 × 109 ^N  · ^{m2 /} C2

Si suponemos un parámetro de impacto b igual al radio de un núcleo de oro,7 × 10 ⁻¹⁵  m , el ángulo de deflexión θ será 2,56 radianes (147°). Si b es igual al radio de un átomo de oro (1,44 × 10 ⁻¹⁰  m ), lo que da como resultado un ángulo de desviación minúsculo de 0,0003 radianes (0,02°). ^{[55] : 109  [60]}

El propio J. J. Thomson no estudió la dispersión de partículas alfa, pero sí la de partículas beta . En su artículo de 1910 "Sobre la dispersión de partículas electrificadas en rápido movimiento", Thomson presentó ecuaciones que modelaban cómo se dispersan las partículas beta en una colisión con un átomo. ^{[61] [8] : 277} Rutherford adaptó esas ecuaciones a la dispersión de partículas alfa en su artículo de 1911 "La dispersión de partículas α y β por la materia y la estructura del átomo".

En el artículo de Thomson de 1910 "Sobre la dispersión de partículas electrificadas en rápido movimiento", Thomson presentó la siguiente ecuación (en la notación de este artículo) que aísla el efecto de la esfera positiva en el modelo de pudín de pasas sobre una partícula beta entrante. ^{[61] [8] : 278}

$${\displaystyle {\bar {\theta }}_{2}={\frac {\pi }{4}}\cdot {\frac {kq_{e}q_{g}}{mv^{2}R}}}$$

Thomson no explicó cómo llegó a esta ecuación, pero esta sección proporciona una conjetura fundamentada y al mismo tiempo adapta la ecuación a la dispersión de partículas alfa. ^[62]

Consideremos una partícula alfa que pasa por una esfera positiva de carga positiva pura (sin electrones) con un radio R y una masa igual a la de un átomo de oro. La partícula alfa pasa lo suficientemente cerca como para rozar el borde de la esfera, que es donde el campo eléctrico de la esfera es más fuerte.

En una sección anterior de este artículo se presentó una ecuación que modela cómo una partícula cargada entrante es desviada por otra partícula cargada en una posición fija.

$${\displaystyle \theta =2\arctan {\frac {kq_{a}q_{g}}{mv^{2}b}}}$$

Esta ecuación se puede utilizar para calcular el ángulo de deflexión en el caso especial de la Figura 4, fijando el parámetro de impacto b en el mismo valor que el radio de la esfera R. Mientras la partícula alfa no penetre en la esfera, no existe ninguna diferencia práctica entre una esfera de carga y una carga puntual.

• q _g = carga positiva del átomo de oro =79  y =1,26 × 10 ⁻¹⁷  C
• q _a = carga de la partícula alfa =2  y =3,20 × 10 ⁻¹⁹  C
• R = radio del átomo de oro =1,44 × 10 ⁻¹⁰  m
• v = velocidad de la partícula alfa =1,53 × 10 ⁷  m/s
• m = masa de la partícula alfa =6,64 × 10 ⁻²⁷  kg
• k = constante de Coulomb =8,987 × 109 ^N  · ^{m2 /} C2

$${\displaystyle \theta _{2}=2\arctan {\frac {kq_{a}q_{g}}{mv^{2}R}}\approx 0.02{\text{ degrees}}}$$

Esto demuestra que la desviación máxima posible será muy pequeña, hasta el punto de que la trayectoria de la partícula alfa es casi una línea recta. Esto nos indica cómo calculamos la desviación media, que será aún menor.

Consideremos una partícula alfa que pasa a través de la esfera positiva de un átomo de oro. La desviación es tan leve que podemos considerar la longitud del recorrido de la partícula a través de la esfera como una cuerda de longitud L.

Dentro de una esfera de carga positiva distribuida uniformemente, la fuerza ejercida sobre la partícula alfa en cualquier punto a lo largo de su trayectoria a través de la esfera es ^{[63] [64] : 106}

$${\displaystyle F={\frac {kq_{a}q_{g}}{r^{2}}}\cdot {\frac {r^{3}}{R^{3}}}}$$

El componente lateral de esta fuerza es

$${\displaystyle F_{y}={\frac {kq_{a}q_{g}}{r^{2}}}\cdot {\frac {r^{3}}{R^{3}}}\cdot \cos \varphi ={\frac {bkq_{a}q_{g}}{R^{3}}}}$$

Por lo tanto, el cambio lateral en el momento p _y es

$${\displaystyle \Delta p_{y}=F_{y}t={\frac {bkq_{a}q_{g}}{R^{3}}}\cdot {\frac {L}{v}}}$$

El ángulo de deflexión viene dado por${\displaystyle \theta _{2}}$

$${\displaystyle \tan \theta _{2}={\frac {\Delta p_{y}}{p_{x}}}={\frac {bkq_{a}q_{g}}{R^{3}}}\cdot {\frac {L}{v}}\cdot {\frac {1}{mv}}}$$

donde p _x es el momento horizontal medio, que primero se reduce y luego se restablece a medida que la fuerza horizontal cambia de dirección cuando la partícula alfa atraviesa la esfera. Como ya sabemos que la desviación es muy pequeña, podemos considerarla igual a . Es obvio que , según el teorema de Pitágoras .${\displaystyle \tan \theta _{2}}$${\displaystyle \theta _{2}}$${\displaystyle L=2{\sqrt {R^{2}-b^{2}}}}$

Para encontrar el ángulo de deflexión promedio , debemos promediar b y L en toda la sección transversal de la esfera:${\displaystyle {\bar {\theta }}_{2}}$

$${\displaystyle {\bar {\theta }}_{2}={\frac {1}{\pi R^{2}}}\int _{0}^{R}{\frac {bkq_{a}q_{g}}{R^{3}}}\cdot {\frac {2{\sqrt {R^{2}-b^{2}}}}{v}}\cdot {\frac {1}{mv}}\cdot 2\pi b\cdot \mathrm {d} b}$$

$${\displaystyle ={\frac {\pi }{4}}\cdot {\frac {kq_{a}q_{g}}{mv^{2}R}}}$$

Esto coincide con la fórmula de Thomson en su artículo de 1910.

Consideremos una partícula alfa que pasa a través de un átomo de radio R siguiendo una trayectoria de longitud L. Se ignora el efecto de la esfera positiva para aislar el efecto de los electrones atómicos. Al igual que con la esfera positiva, esperamos que la desviación de los electrones sea muy pequeña hasta el punto de que la trayectoria sea prácticamente una línea recta.

Para los electrones dentro de una distancia arbitraria s de la trayectoria de la partícula alfa, su distancia media será1/2⁠ s . Por lo tanto, la desviación media por electrón será

$${\displaystyle 2\arctan {\frac {kq_{a}q_{e}}{mv^{2}{\tfrac {1}{2}}s}}\approx {\frac {4kq_{a}q_{e}}{mv^{2}s}}}$$

donde q _e es la carga elemental . La desviación neta promedio de todos los electrones dentro de este cilindro arbitrario de efecto alrededor de la trayectoria de la partícula alfa es

$${\displaystyle \theta _{1}={\frac {4kq_{a}q_{e}}{mv^{2}s}}{\sqrt {N_{0}\pi s^{2}L}}}$$

donde N ₀ es el número de electrones por unidad de volumen y es el volumen de este cilindro.${\displaystyle \pi s^{2}L}$

Dado que tratamos a L como una línea recta, entonces donde b es la distancia de esta línea desde el centro. La media de es por lo tanto${\displaystyle L=2{\sqrt {R^{2}-b^{2}}}}$${\displaystyle {\sqrt {L}}}$

$${\displaystyle {\frac {1}{\pi R^{2}}}\int _{0}^{R}{\sqrt {2{\sqrt {R^{2}-b^{2}}}}}\cdot 2\pi b\cdot \mathrm {d} b={\frac {4}{5}}{\sqrt {2R}}}$$

Ahora podemos reemplazar en la ecuación para obtener la deflexión media :${\displaystyle {\sqrt {L}}}$${\displaystyle \theta _{1}}$${\displaystyle {\bar {\theta }}_{1}}$

$${\displaystyle {\bar {\theta }}_{1}={\frac {4kq_{a}q_{e}}{mv^{2}s}}{\sqrt {N_{0}\pi s^{2}}}\cdot {\frac {4}{5}}{\sqrt {2R}}}$$

$${\displaystyle ={\frac {16}{5}}\cdot {\frac {kq_{a}q_{e}}{mv^{2}R}}{\sqrt {\frac {3N}{2}}}}$$

donde N es el número de electrones en el átomo, igual a .${\displaystyle N_{0}{\tfrac {4}{3}}\pi R^{3}}$

Ahora aplicamos las ecuaciones de Thomson descritas anteriormente a una partícula alfa que choca con un átomo de oro, utilizando los siguientes valores:

• q _g = carga positiva del átomo de oro =79  q _e =1,26 × 10 ⁻¹⁷  C
• q _a = carga de la partícula alfa =2  q _e =3,20 × 10 ⁻¹⁹  C
• q _e = carga elemental =1,602 × 10 ⁻¹⁹  C
• R = radio del átomo de oro =1,44 × 10 ⁻¹⁰  m
• v = velocidad de la partícula alfa =1,53 × 10 ⁷  m/s
• m = masa de la partícula alfa =6,64 × 10 ⁻²⁷  kg
• k = constante de Coulomb =8,987 × 109 ^N  · ^{m2 /} C2
• N = número de electrones en el átomo de oro = 79

El ángulo promedio con el que la partícula alfa debe ser desviada por los electrones atómicos es:

$${\displaystyle {\bar {\theta }}_{1}={\frac {16}{5}}\cdot {\frac {kq_{a}q_{e}}{mv^{2}R}}{\sqrt {\frac {3N}{2}}}\approx 0.00007{\text{ radians or }}0.004{\text{ degrees}}}$$

El ángulo promedio con el que una partícula alfa debe ser desviada por la esfera positiva es:

$${\displaystyle {\bar {\theta }}_{2}={\frac {\pi }{4}}\cdot {\frac {kq_{a}q_{g}}{mv^{2}R}}\approx 0.00013{\text{ radians or 0.007 degrees}}}$$

La desviación neta para una sola colisión atómica es:

$${\displaystyle {\bar {\theta }}={\sqrt {{\bar {\theta }}_{1}^{2}+{\bar {\theta }}_{2}^{2}}}\approx 0.008{\text{ degrees}}}$$

En promedio, tanto la esfera positiva como los electrones proporcionan muy poca desviación en una sola colisión. El modelo de Thomson combinó muchos eventos de dispersión única de los electrones del átomo y una esfera positiva. Cada colisión puede aumentar o disminuir el ángulo de dispersión total. Solo en muy raras ocasiones una serie de colisiones se alinearían todas en la misma dirección. El resultado es similar al problema estadístico estándar llamado paseo aleatorio . Si el ángulo de desviación promedio de la partícula alfa en una sola colisión con un átomo es , entonces la desviación promedio después de n colisiones es${\displaystyle {\bar {\theta }}}$

$${\displaystyle {\bar {\theta }}_{n}={\bar {\theta }}{\sqrt {n}}}$$

La probabilidad de que una partícula alfa se desvíe un total de más de 90° después de n desviaciones viene dada por:

$${\displaystyle e^{-(90/{\bar {\theta }}_{n})^{2}}}$$

donde e es el número de Euler (≈2,71828...). Suponiendo una desviación media por colisión de 0,008°, y por tanto una desviación media de 0,8° tras 10.000 colisiones, la probabilidad de que una partícula alfa se desvíe más de 90° será ^{[64] : 109}

$${\displaystyle e^{-(90/0.8)^{2}}\approx e^{-12656}\approx 10^{-5946}}$$

Si bien en el modelo del pudín de pasas de Thomson es matemáticamente posible que una partícula alfa pueda desviarse más de 90° después de 10.000 colisiones, la probabilidad de que se produzca tal acontecimiento es tan baja que resulta indetectable. Este número extremadamente pequeño demuestra que el modelo de Thomson no puede explicar los resultados del experimento de Geiger-Mardsen de 1909.

Rutherford asumió que el radio de los átomos en general era del orden de 10 ⁻¹⁰ m y que la carga positiva de un átomo de oro era aproximadamente 100 veces la del hidrógeno (100  q _e ). ^[40] Se sabía que el peso atómico del oro rondaba los 197 desde principios del siglo XIX. ^[65] A partir de un experimento de 1906, Rutherford midió que las partículas alfa tenían una carga de2  q _e y un peso atómico de 4, y las partículas alfa emitidas por el radón tienen una velocidad de1,70 × 10 ⁷  m/s . ^[66] Sin embargo, antes del artículo de Rutherford de 1911, todavía se pensaba que la partícula alfa tenía el tamaño de un átomo y contenía hasta 10 electrones. ^{[8] : 285} En esta época se informaron muchos valores diferentes de la carga elemental ( q _e ), pero los valores variaban considerablemente. Rutherford planeó resolver este problema en 1907 con nuevos experimentos sobre partículas alfa, pero su enfoque se vio frustrado por la dispersión, lo que finalmente lo llevó a sugerir los experimentos de Geiger-Marsden. ^{[8] : 261} Jean Perrin en 1909 midió la masa del hidrógeno en1,43 × 10 ⁻²⁷  kg , ^[67] y si las partículas alfa son cuatro veces más pesadas que eso, tendrían una masa absoluta de5,72 × 10 ⁻²⁷  kg .

En la época de Rutherford, la convención era medir la carga en unidades electrostáticas , la distancia en centímetros, la fuerza en dinas y la energía en ergios . La convención moderna es medir la carga en culombios , la distancia en metros, la fuerza en newtons y la energía en julios . El uso de culombios requiere el uso de la constante de Coulomb ( k ) en las ecuaciones. En este artículo, las ecuaciones de Rutherford y Thomson se han reescrito para que se ajusten a las convenciones de notación modernas.

• Teoría atómica
• Espectroscopia de retrodispersión de Rutherford
• Lista de experimentos de dispersión

• "El mundo nuclear de Rutherford: la historia del descubrimiento del núcleo". Instituto Americano de Física . Consultado el 23 de octubre de 2014 .
• "Dispersión de Rutherford". HyperPhysics . Universidad Estatal de Georgia . Consultado el 13 de agosto de 2014 .
• Arthur Beiser (1969). Perspectivas de la física moderna. McGraw-Hill Book Company.
• Arthur Stewart Eve (1939). Rutherford: La vida y las cartas del honorable Lord Rutherford, OM MacMillan.
• Ernest Rutherford (1899). "Radiación de uranio y la conducción eléctrica que produce" (PDF) . Philosophical Magazine . 47 (284): 109–163.
• Ernest Rutherford (1911). "La dispersión de partículas α y β por la materia y la estructura del átomo" (PDF) . Philosophical Magazine . Serie 6. 21 (125): 669–688. doi :10.1080/14786440508637080.
• Ernest Rutherford (1906). "La masa y la velocidad de las partículas α expulsadas del radio y el actinio". Revista filosófica . Serie 6. 12 (70): 348–371. doi :10.1080/14786440609463549.
• Ernest Rutherford (1912). «El origen de los rayos β y γ a partir de sustancias radiactivas». Revista filosófica . Serie 6. 24 (142): 453–462. doi :10.1080/14786441008637351.
• Ernest Rutherford; John Mitchell Nuttal (1913). "Dispersión de partículas α por gases". Revista filosófica . Serie 6. 26 (154): 702–712. doi :10.1080/14786441308635014.
• Ernest Rutherford (1914). "La estructura del átomo". Revista filosófica . Serie 6. 27 (159): 488–498. doi :10.1080/14786440308635117.
• Ernest Rutherford (1938). "Cuarenta años de física". En Needham, Joseph; Pagel, Walter (eds.). Antecedentes de la ciencia moderna: diez conferencias en Cambridge organizadas por el Comité de Historia de la Ciencia 1936. Cambridge University Press .
• Ernest Rutherford (1913). Sustancias radiactivas y sus radiaciones. Cambridge University Press .
• Ernest Rutherford (1936). "Radioactividad y estructura atómica". Revista de la Sociedad Química . 1936 : 508–516. doi :10.1039/JR9360000508.
• "Geiger y Marsden". Laboratorio Cavendish . Archivado desde el original el 6 de octubre de 2014. Consultado el 23 de julio de 2014 .
• John Daintith; Derek Gjertsen (1999). Diccionario de científicos. Oxford University Press . ISBN 978-0-19-280086-2.
• Michael Fowler. "Dispersión de Rutherford". Apuntes de clase de Física 252. Universidad de Virginia . Consultado el 23 de julio de 2014 .
• Hans Geiger (1908). "Sobre la dispersión de partículas α por la materia". Actas de la Royal Society of London A . 81 (546): 174–177. Bibcode :1908RSPSA..81..174G. doi : 10.1098/rspa.1908.0067 .
• Hans Geiger; Ernest Marsden (1909). "Sobre una reflexión difusa de las partículas α". Actas de la Royal Society of London A . 82 (557): 495–500. Bibcode :1909RSPSA..82..495G. doi : 10.1098/rspa.1909.0054 .
• Hans Geiger (1910). "La dispersión de las partículas α por la materia". Actas de la Royal Society of London A . 83 (565): 492–504. Bibcode :1910RSPSA..83..492G. doi : 10.1098/rspa.1910.0038 .
• Hans Geiger; Ernest Marsden (1913). "Las leyes de deflexión de partículas α a través de grandes ángulos" (PDF) . Revista filosófica . Serie 6. 25 (148): 604–623. doi :10.1080/14786440408634197.
• John L. Heilbron (enero de 1968). «La dispersión de partículas α y β y el átomo de Rutherford». Archivo de Historia de las Ciencias Exactas . 4 (4): 247–307. doi :10.1007/BF00411591.
• John L. Heilbron (2003). Ernest Rutherford y la explosión de átomos . Oxford University Press . ISBN 978-0-19-512378-4.
• John W. Jewett Jr.; Raymond A. Serway (2014). "Modelos tempranos del átomo". Física para científicos e ingenieros con Física moderna (novena edición). Brooks/Cole. pág. 1299.
• Joy Manners (2000). Física cuántica: una introducción. CRC Press. ISBN 978-0-7503-0720-8.
• Hantaro Nagaoka (1904). "Cinética de un sistema de partículas que ilustra el espectro de líneas y bandas y los fenómenos de la radiactividad". Revista filosófica . Serie 6. 7 (41): 445–455. doi :10.1080/14786440409463141.
• Richard Reeves (2008). Una fuerza de la naturaleza: el genio de la frontera de Ernest Rutherford . WW Norton & Co. ISBN 978-0-393-07604-2.
• JA Crowther (1910). "Sobre la dispersión de rayos β homogéneos y el número de electrones en el átomo". Actas de la Royal Society de Londres . 84 (570): 226–247. Bibcode :1910RSPSA..84..226C. doi :10.1098/rspa.1910.0074.
• Joseph J. Thomson (1904). "Sobre la estructura del átomo: una investigación de la estabilidad y los períodos de oscilación de un número de corpúsculos dispuestos a intervalos iguales alrededor de la circunferencia de un círculo; con aplicación de los resultados a la teoría de la estructura atómica". Revista filosófica . Serie 6. 7 (39): 237. doi :10.1080/14786440409463107.
• JJ Thomson (1906). "Sobre el número de corpúsculos en un átomo" (PDF) . Revista filosófica . 6. 11 (66): 769–781. doi :10.1080/14786440609463496.
• JJ Thomson (1910). "Sobre la dispersión de partículas electrificadas en rápido movimiento". Actas de la Sociedad Filosófica de Cambridge . 15 : 465–471.
• Gary Tibbetts (2007). Cómo razonaron los grandes científicos: el método científico en acción . Elsevier . ISBN 978-0-12-398498-2.
• Jean Perrin (1910) [1909]. Movimiento browniano y realidad molecular. Traducido por F. Soddy. Taylor y Francis.
• EA Davis; IJ Falconer (1997). JJ Thomson y el descubrimiento del electrón . Taylor & Francis. ISBN 0-7484-0720-0.
• Giora Hon; Bernard R. Goldstein (6 de septiembre de 2013). "El modelo atómico del budín de pasas de JJ Thomson: la creación de un mito científico". Annalen der Physik . 525 (8–9): A129–A133. Bibcode :2013AnP...525A.129H. doi :10.1002/andp.201300732.
• JJ Thomson (1907). La teoría corpuscular de la materia. Charles Scribner's Sons.
• Goldstein, Herbert ; Poole, Charles; Safko, John (2002). Mecánica clásica (tercera edición). Addison-Wesley. ISBN 978-0-201-65702-9.
• Tong, David. "Conferencias sobre dinámica y relatividad". Universidad de Cambridge . Consultado el 14 de julio de 2024 .| Capítulo 4 Fuerzas centrales

• Descripción del experimento, de cambridgephysics.org