5-ortoplexes runcinados

5-ortoplex	5-ortoplex runcinado	5 cubos runcinados
Ortoplex 5-runcitruncado	5-ortoplex runcicantelado	5-ortoplex antitruncado de Runcic
Cubo de 5 truncados	5 cubos runcicantelados	Cubo de 5 truncados Runcicanti
Proyecciones ortogonales en el plano B 5 de Coxeter

En geometría de cinco dimensiones , un 5-ortoplex runcinado es un 5-politopo uniforme convexo con truncamiento de tercer orden ( runcinación ) del 5-ortoplex regular .

Hay 8 runcinaciones del 5-ortoplex con permutaciones de truncamientos y cantelaciones . Cuatro son de construcción más simple en relación con el 5-cubo .

5-ortoplex runcinado
Tipo	Politopo 5 uniforme
Símbolo de Schläfli	t0,3 { 3,3,3,4}
Diagrama de Coxeter-Dynkin
4 caras	162
Células	1200
Caras	2160
Bordes	1440
Vértices	320
Figura de vértice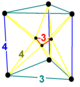
Grupo Coxeter	B 5 [4,3,3,3] D 5 [3 2,1,1 ]
Propiedades	convexo

• Pentacross runcinado
• Triacontiditero pequeño prismático (acrónimo: spat) (Jonathan Bowers) ^[1]

Los vértices del se pueden realizar en el espacio de 5, como permutaciones y combinaciones de signos de:

(0,1,1,1,2)

proyecciones ortográficas

Avión Coxeter	B 5	B4 / D5​	B3 / D4 / A2​
Gráfico
Simetría diedral	[10]	[8]	[6]
Avión Coxeter	B2​	Un 3
Gráfico
Simetría diedral	[4]	[4]

Ortoplex 5-runcitruncado
Tipo	5-politopo uniforme
Símbolo de Schläfli	t0,1,3 {3,3,3,4 } t0,1,3 { 3,3 1,1 }
Diagramas de Coxeter-Dynkin
4 caras	162
Células	1440
Caras	3680
Bordes	3360
Vértices	960
Figura de vértice
Grupos de Coxeter	B 5 , [3,3,3,4] D 5 , [3 2,1,1 ]
Propiedades	convexo

• Pentacross truncado y runcitruncado
• Triacontiditerona prismatruncada (acrónimo: pattit) (Jonathan Bowers) ^[2]

Las coordenadas cartesianas para los vértices de un 5-ortoplex runcitruncado, centrado en el origen, son todos los 80 vértices que son permutaciones de signo (4) y coordenada (20) de

(±3,±2,±1,±1,0)

proyecciones ortográficas

Avión Coxeter	B 5	B4 / D5​	B3 / D4 / A2​
Gráfico
Simetría diedral	[10]	[8]	[6]
Avión Coxeter	B2​	Un 3
Gráfico
Simetría diedral	[4]	[4]

5-ortoplex runcicantelado
Tipo	Politopo 5 uniforme
Símbolo de Schläfli	t0,2,3 {3,3,3,4 } t0,2,3 { 3,3,3 1,1 }
Diagrama de Coxeter-Dynkin
4 caras	162
Células	1200
Caras	2960
Bordes	2880
Vértices	960
Figura de vértice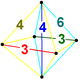
Grupo Coxeter	B 5 [4,3,3,3] D 5 [3 2,1,1 ]
Propiedades	convexo

• Pentacross runcicantelado
• Triacontiditeron prismatorrombado (acrónimo: pirt) (Jonathan Bowers) ^[3]

Los vértices del 5-ortoplex runcicantelado se pueden realizar en el 5-espacio, como permutaciones y combinaciones de signos de:

(0,1,2,2,3)

proyecciones ortográficas

Avión Coxeter	B 5	B4 / D5​	B3 / D4 / A2​
Gráfico
Simetría diedral	[10]	[8]	[6]
Avión Coxeter	B2​	Un 3
Gráfico
Simetría diedral	[4]	[4]

5-ortoplex antitruncado de Runcic
Tipo	Politopo 5 uniforme
Símbolo de Schläfli	t0,1,2,3 { 3,3,3,4 }
Diagrama de Coxeter-Dynkin
4 caras	162
Células	1440
Caras	4160
Bordes	4800
Vértices	1920
Figura de vértice	5 celdas irregulares
Grupos de Coxeter	B 5 [4,3,3,3] D 5 [3 2,1,1 ]
Propiedades	convexo , isogonal

• Pentacross antitruncado Runcic
• Gran triacontiditeron prismático (gippit) (Jonathan Bowers) ^[4]

Las coordenadas cartesianas de los vértices de un 5-ortoplex runcicantitruncado que tiene una longitud de arista de √ 2 están dadas por todas las permutaciones de coordenadas y signo de:

${\displaystyle \left(0,1,2,3,4\right)}$

proyecciones ortográficas

Avión Coxeter	B 5	B4 / D5​	B3 / D4 / A2​
Gráfico
Simetría diedral	[10]	[8]	[6]
Avión Coxeter	B2​	Un 3
Gráfico
Simetría diedral	[4]	[4]

El 5-demicubo romo definido como una alternancia del 5-demicubo omnitruncado no es uniforme, pero se puede dar un diagrama de Coxeter.oy simetría [3 ^2,1,1 ] ⁺ o [4,(3,3,3) ⁺ ], y construida a partir de 10 celdas chatas de 24 , 32 celdas chatas de 5 , 40 antiprismas tetraédricos chatos , 80 duoantiprismas de 2-3 y 960 celdas irregulares de 5 que llenan los huecos en los vértices eliminados.

Este politopo es uno de los 31 5-politopos uniformes generados a partir del 5-cubo o 5-ortoplex regular .

Politopos B5
β5​	t1β5​​​	t2γ5​​​	t1γ5​​​	γ5​	t 0,1 β 5	t0,2β5​​​	t1,2β5​​​
t0,3β5​​​	t1,3γ5​​​	t1,2γ5​​​	t 0,4 γ 5	t 0,3 γ ​​5	t 0,2 γ 5	t 0,1 γ 5	t0,1,2β5​​​
t0,1,3β5​​​	t0,2,3β5​​​	t1,2,3γ5​​​	t0,1,4β5​​​	t0,2,4γ5​​​	t0,2,3γ5​​​	t 0,1,4 γ 5	t 0,1,3 γ 5
t 0,1,2 γ 5	t0,1,2,3β5​​​	t0,1,2,4β5​​​	t0,1,3,4γ5​​​	t 0,1,2,4 γ 5	t0,1,2,3γ5​​​	t 0,1,2,3,4 γ 5

• HSM Coxeter :
  • HSM Coxeter, Politopos regulares , 3.ª edición, Dover, Nueva York, 1973
  • Caleidoscopios: escritos selectos de HSM Coxeter , editado por F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN  978-0-471-01003-6 [1]
    • (Artículo 22) HSM Coxeter, Politopos regulares y semirregulares I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Artículo 23) HSM Coxeter, Politopos regulares y semirregulares II , [Math. Zeit. 188 (1985) 559-591]
    • (Artículo 24) HSM Coxeter, Politopos regulares y semirregulares III , [Math. Zeit. 200 (1988) 3-45]
• Manuscrito de politopos uniformes de Norman Johnson (1991)
  • NW Johnson: La teoría de politopos uniformes y panales , Ph.D.
• Klitzing, Richard. "Polítopos uniformes 5D (politera)".x3o3o3x4o - escupió, x3x3o3x4o - pattit, x3o3x3x4o - pirt, x3x3x3x4o - gippit

• Glosario del hiperespacio, George Olshevsky.
• Politopos de varias dimensiones, Jonathan Bowers
  • Políteros uniformes runcinados (spid), Jonathan Bowers
• Glosario multidimensional