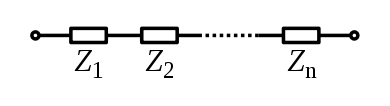Impedancia eléctrica

Artículos sobre
Electromagnetismo
Electricidad Magnetismo Óptica Historia Computacional Libros de texto Fenómenos
Electrostática Densidad de carga Conductor Ley de Coulomb Electreto Carga eléctrica Dipolo eléctrico Campo eléctrico Flujo eléctrico Potencial eléctrico Descarga electrostática Inducción electrostática Ley de Gauss Aislante Permitividad Polarización Energía potencial Electricidad estática Triboelectricidad
Magnetostática Ley de Ampère Ley de Biot-Savart Ley magnética de Gauss Dipolo magnético Campo magnético Flujo magnético Potencial escalar magnético Potencial vectorial magnético Magnetización Permeabilidad Regla de la mano derecha
Electrodinámica Radiación de frenado Radiación ciclotrónica Corriente de desplazamiento Corriente de Foucault Campo electromagnético Inducción electromagnética Pulso electromagnético Radiación electromagnética Ley de Faraday Ecuaciones de Jefimenko Fórmula de Larmor Ley de Lenz Potencial de Liénard-Wiechert Ecuaciones de Londres Fuerza de Lorentz Ecuaciones de Maxwell Tensor de Maxwell Vector de Poynting Radiación de sincrotrón
Red eléctrica Corriente alterna Capacidad Densidad de corriente Corriente continua Corriente eléctrica Energía eléctrica Electrólisis Electromotive force Impedance Inductance Joule heating Kirchhoff laws Network analysis Ohm law Parallel circuit Resistance Resonant cavities Series circuit Voltage Watt Waveguides
Magnetic circuit AC motor DC motor Electric machine Electric motor Gyrator–capacitor Induction motor Linear motor Magnetomotive force Permeance Reluctance (complex) Reluctance (real) Rotor Stator Transformer
Covariant formulation Electromagnetic tensor Electromagnetism and special relativity Four-current Four-potential Mathematical descriptions Maxwell equations in curved spacetime Relativistic electromagnetism Stress–energy tensor
Scientists Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Helmholtz Henry Hertz Hopkinson Jefimenko Joule Kelvin Kirchhoff Larmor Lenz Liénard Lorentz Maxwell Neumann Ohm Ørsted Poisson Poynting Ritchie Savart Singer Steinmetz Tesla Thomson Volta Weber Wiechert
v t e

En ingeniería eléctrica , la impedancia es la oposición a la corriente alterna presentada por el efecto combinado de la resistencia y la reactancia en un circuito . ^[1]

Cuantitativamente, la impedancia de un elemento de circuito de dos terminales es la relación entre la representación compleja del voltaje sinusoidal entre sus terminales y la representación compleja de la corriente que fluye a través de él. ^[2] En general, depende de la frecuencia del voltaje sinusoidal.

La impedancia extiende el concepto de resistencia a los circuitos de corriente alterna (CA) y posee tanto magnitud como fase , a diferencia de la resistencia, que solo tiene magnitud.

La impedancia se puede representar como un número complejo , con las mismas unidades que la resistencia, para la cual la unidad del SI es el ohmio ( Ω ). Su símbolo es generalmente Z y se puede representar escribiendo su magnitud y fase en la forma polar | Z | ∠θ . Sin embargo, la representación de números complejos cartesianos suele ser más eficaz para fines de análisis de circuitos.

La noción de impedancia es útil para realizar análisis de CA de redes eléctricas , ya que permite relacionar voltajes y corrientes sinusoidales mediante una ley lineal simple. En redes con múltiples puertos , la definición de impedancia de dos terminales es inadecuada, pero los voltajes complejos en los puertos y las corrientes que fluyen a través de ellos aún están relacionados linealmente mediante la matriz de impedancia . ^[3]

El recíproco de la impedancia es la admitancia , cuya unidad SI es el siemens , antiguamente llamado mho .

Los instrumentos utilizados para medir la impedancia eléctrica se denominan analizadores de impedancia .

Tal vez el primer uso de números complejos en el análisis de circuitos fue realizado por Johann Victor Wietlisbach en 1879 al analizar el puente de Maxwell . Wietlisbach evitó el uso de ecuaciones diferenciales al expresar corrientes y voltajes de CA como funciones exponenciales con exponentes imaginarios (ver § Validez de la representación compleja). Wietlisbach descubrió que el voltaje requerido se daba al multiplicar la corriente por un número complejo (impedancia), aunque no lo identificó como un parámetro general por derecho propio. ^[4]

El término impedancia fue acuñado por Oliver Heaviside en julio de 1886. ^{[5] [6]} Heaviside reconoció que el "operador de resistencia" (impedancia) en su cálculo operacional era un número complejo. En 1887 demostró que existía un equivalente en corriente alterna a la ley de Ohm . ^[7]

En 1893, Arthur Kennelly publicó un influyente artículo sobre la impedancia. Kennelly llegó a una representación de números complejos de una manera bastante más directa que utilizando funciones exponenciales imaginarias. Kennelly siguió la representación gráfica de la impedancia (que muestra la resistencia, la reactancia y la impedancia como las longitudes de los lados de un triángulo rectángulo) desarrollada por John Ambrose Fleming en 1889. De este modo, las impedancias se podían sumar vectorialmente . Kennelly se dio cuenta de que esta representación gráfica de la impedancia era directamente análoga a la representación gráfica de números complejos ( diagrama de Argand ). De este modo, los problemas en el cálculo de la impedancia se podían abordar algebraicamente con una representación de números complejos. ^{[8] [9]} Más tarde ese mismo año, el trabajo de Kennelly se generalizó a todos los circuitos de CA por Charles Proteus Steinmetz . Steinmetz no solo representó impedancias mediante números complejos, sino también voltajes y corrientes. A diferencia de Kennelly, Steinmetz fue capaz de expresar equivalentes en corriente alterna de leyes de corriente continua, como las leyes de Ohm y Kirchhoff. ^[10] El trabajo de Steinmetz fue muy influyente en la difusión de la técnica entre los ingenieros. ^[11]

Además de la resistencia que se observa en los circuitos de CC, la impedancia en los circuitos de CA incluye los efectos de la inducción de voltajes en los conductores por los campos magnéticos ( inductancia ) y el almacenamiento electrostático de carga inducido por voltajes entre conductores ( capacidad ). La impedancia causada por estos dos efectos se conoce colectivamente como reactancia y forma la parte imaginaria de la impedancia compleja, mientras que la resistencia forma la parte real .

La impedancia de un elemento de circuito de dos terminales se representa como una cantidad compleja . La forma polar captura convenientemente las características de magnitud y fase como${\displaystyle Z}$

${\displaystyle \ Z=|Z|e^{j\arg(Z)}}$

donde la magnitud representa la relación entre la amplitud de la diferencia de voltaje y la amplitud de la corriente, mientras que el argumento (comúnmente representado por el símbolo ) da la diferencia de fase entre el voltaje y la corriente. es la unidad imaginaria , y se utiliza en lugar de en este contexto para evitar confusiones con el símbolo de corriente eléctrica . ^{[12] : 21}${\displaystyle |Z|}$${\displaystyle \arg(Z)}$${\displaystyle \theta }$${\displaystyle j}$${\displaystyle i}$

En forma cartesiana , la impedancia se define como

${\displaystyle \ Z=R+jX}$

donde la parte real de la impedancia es la resistencia R y la parte imaginaria es la reactancia X.

Cuando es necesario sumar o restar impedancias, la forma cartesiana es más conveniente; pero cuando se multiplican o dividen cantidades, el cálculo se vuelve más simple si se utiliza la forma polar. Un cálculo de circuito, como encontrar la impedancia total de dos impedancias en paralelo, puede requerir la conversión entre formas varias veces durante el cálculo. La conversión entre las formas sigue las reglas de conversión normales de números complejos .

Para simplificar los cálculos, las ondas de voltaje y corriente sinusoidales se representan comúnmente como funciones de tiempo de valor complejo denotadas como y . ^{[13] [14]}${\displaystyle V}$${\displaystyle I}$

${\displaystyle {\begin{aligned}V&=|V|e^{j(\omega t+\phi _{V})},\\I&=|I|e^{j(\omega t+\phi _{I})}.\end{aligned}}}$

La impedancia de un circuito bipolar se define como la relación de estas cantidades:

${\displaystyle Z={\frac {V}{I}}={\frac {|V|}{|I|}}e^{j(\phi _{V}-\phi _{I})}.}$

Por lo tanto, denotando , tenemos${\displaystyle \theta =\phi _{V}-\phi _{I}}$

${\displaystyle {\begin{aligned}|V|&=|I||Z|,\\\phi _{V}&=\phi _{I}+\theta .\end{aligned}}}$

La ecuación de magnitud es la conocida ley de Ohm aplicada a las amplitudes de voltaje y corriente, mientras que la segunda ecuación define la relación de fase.

Esta representación mediante exponenciales complejas puede justificarse observando que (por la fórmula de Euler ):

${\displaystyle \ \cos(\omega t+\phi )={\frac {1}{2}}{\Big [}e^{j(\omega t+\phi )}+e^{-j(\omega t+\phi )}{\Big ]}}$

La función sinusoidal de valor real que representa voltaje o corriente se puede dividir en dos funciones de valor complejo. Por el principio de superposición , podemos analizar el comportamiento de la sinusoide del lado izquierdo analizando el comportamiento de los dos términos complejos del lado derecho. Dada la simetría, solo necesitamos realizar el análisis para un término del lado derecho. Los resultados son idénticos para el otro. Al final de cualquier cálculo, podemos volver a las sinusoides de valor real observando además que

${\displaystyle \ \cos(\omega t+\phi )=\operatorname {\mathcal {R_{e}}} {\Big \{}e^{j(\omega t+\phi )}{\Big \}}}$

El significado de la impedancia eléctrica se puede entender sustituyéndola en la ley de Ohm. ^{[15] [16]} Suponiendo que un elemento de circuito de dos terminales con impedancia es impulsado por un voltaje o corriente sinusoidal como el anterior, se cumple ${\displaystyle Z}$

${\displaystyle \ V=IZ=I|Z|e^{j\arg(Z)}}$

La magnitud de la impedancia actúa como una resistencia, dando la caída en la amplitud del voltaje a través de una impedancia para una corriente dada . El factor de fase nos dice que la corriente está retrasada respecto del voltaje por una fase (es decir, en el dominio del tiempo , la señal de corriente se desplaza más tarde con respecto a la señal de voltaje).${\displaystyle |Z|}$${\displaystyle Z}$${\displaystyle I}$${\displaystyle \theta =\arg(Z)}$${\textstyle {\frac {\theta }{2\pi }}T}$

Así como la impedancia extiende la ley de Ohm para cubrir circuitos de CA, otros resultados del análisis de circuitos de CC, como la división de voltaje , la división de corriente , el teorema de Thévenin y el teorema de Norton , también se pueden extender a circuitos de CA reemplazando la resistencia por impedancia.

Un fasor se representa mediante un número complejo constante, generalmente expresado en forma exponencial, que representa la amplitud compleja (magnitud y fase) de una función sinusoidal del tiempo. Los ingenieros eléctricos utilizan fasores para simplificar los cálculos que involucran senos (como en circuitos de CA ^{[12] : 53} ), donde a menudo pueden reducir un problema de ecuación diferencial a uno algebraico.

La impedancia de un elemento de circuito se puede definir como la relación entre el voltaje fasorial a través del elemento y la corriente fasorial a través del elemento, determinada por las amplitudes y fases relativas del voltaje y la corriente. Esto es idéntico a la definición de la ley de Ohm dada anteriormente, reconociendo que los factores de se cancelan.${\displaystyle e^{j\omega t}}$

La impedancia de una resistencia ideal es puramente real y se llama impedancia resistiva :

${\displaystyle \ Z_{R}=R}$

En este caso, las formas de onda de voltaje y corriente son proporcionales y están en fase.

Los inductores y condensadores ideales tienen una impedancia reactiva puramente imaginaria :

La impedancia de los inductores aumenta a medida que aumenta la frecuencia;

${\displaystyle Z_{L}=j\omega L}$^[a]

La impedancia de los condensadores disminuye a medida que aumenta la frecuencia;

${\displaystyle Z_{C}={\frac {1}{j\omega C}}}$

En ambos casos, para una tensión sinusoidal aplicada, la corriente resultante también es sinusoidal, pero en cuadratura , desfasada 90 grados con respecto a la tensión. Sin embargo, las fases tienen signos opuestos: en un inductor, la corriente va en atraso ; en un condensador, la corriente va en adelanto .

Tenga en cuenta las siguientes identidades para la unidad imaginaria y su recíproco:

${\displaystyle {\begin{aligned}j&\equiv \cos {\left({\frac {\pi }{2}}\right)}+j\sin {\left({\frac {\pi }{2}}\right)}\equiv e^{j{\frac {\pi }{2}}}\\{\frac {1}{j}}\equiv -j&\equiv \cos {\left(-{\frac {\pi }{2}}\right)}+j\sin {\left(-{\frac {\pi }{2}}\right)}\equiv e^{j\left(-{\frac {\pi }{2}}\right)}\end{aligned}}}$

De esta manera, las ecuaciones de impedancia del inductor y del condensador se pueden reescribir en forma polar:

${\displaystyle {\begin{aligned}Z_{L}&=\omega Le^{j{\frac {\pi }{2}}}\\Z_{C}&={\frac {1}{\omega C}}e^{j\left(-{\frac {\pi }{2}}\right)}\end{aligned}}}$

La magnitud da el cambio en la amplitud de voltaje para una amplitud de corriente dada a través de la impedancia, mientras que los factores exponenciales dan la relación de fase.

Lo que sigue a continuación es una derivación de la impedancia para cada uno de los tres elementos básicos del circuito : la resistencia, el condensador y el inductor. Aunque la idea se puede ampliar para definir la relación entre el voltaje y la corriente de cualquier señal arbitraria , estas derivaciones suponen señales sinusoidales . De hecho, esto se aplica a cualquier señal periódica arbitraria, porque estas se pueden aproximar como una suma de senos a través del análisis de Fourier .

Para una resistencia, existe la relación

${\displaystyle v_{\text{R}}{\mathord {\left(t\right)}}=i_{\text{R}}{\mathord {\left(t\right)}}R}$

cual es la ley de Ohm .

Considerando que la señal de voltaje es

${\displaystyle v_{\text{R}}(t)=V_{p}\sin(\omega t)}$

resulta que

${\displaystyle {\frac {v_{\text{R}}{\mathord {\left(t\right)}}}{i_{\text{R}}{\mathord {\left(t\right)}}}}={\frac {V_{p}\sin(\omega t)}{I_{p}\sin {\mathord {\left(\omega t\right)}}}}=R}$

Esto dice que la relación entre la amplitud del voltaje de CA y la amplitud de la corriente alterna (CA) a través de una resistencia es , y que el voltaje de CA adelanta la corriente a través de una resistencia en 0 grados.${\displaystyle R}$

Este resultado se expresa comúnmente como

${\displaystyle Z_{\text{resistor}}=R}$

Para un condensador, existe la relación:

${\displaystyle i_{\text{C}}(t)=C{\frac {\mathrm {d} v_{\text{C}}(t)}{\mathrm {d} t}}}$

Considerando que la señal de voltaje es

${\displaystyle v_{\text{C}}(t)=V_{p}e^{j\omega t}}$

resulta que

${\displaystyle {\frac {\mathrm {d} v_{\text{C}}(t)}{\mathrm {d} t}}=j\omega V_{p}e^{j\omega t}}$

y así, como anteriormente,

${\displaystyle Z_{\text{capacitor}}={\frac {v_{\text{C}}{\mathord {\left(t\right)}}}{i_{\text{C}}{\mathord {\left(t\right)}}}}={\frac {1}{j\omega C}}.}$

Por el contrario, si se supone que la corriente a través del circuito es sinusoidal, su representación compleja es

${\displaystyle i_{\text{C}}(t)=I_{p}e^{j\omega t}}$

Luego integramos la ecuación diferencial

${\displaystyle i_{\text{C}}(t)=C{\frac {\mathrm {d} v_{\text{C}}(t)}{\mathrm {d} t}}}$

conduce a

${\displaystyle v_{C}(t)={\frac {1}{j\omega C}}I_{p}e^{j\omega t}+{\text{Const.}}={\frac {1}{j\omega C}}i_{C}(t)+{\text{Const.}}}$

El término Const representa una polarización de potencial fija superpuesta al potencial sinusoidal de CA, que no desempeña ningún papel en el análisis de CA. Para este propósito, se puede suponer que este término es 0, por lo tanto, nuevamente la impedancia

${\displaystyle Z_{\text{capacitor}}={\frac {1}{j\omega C}}.}$

Para el inductor, tenemos la relación (de la ley de Faraday ):

${\displaystyle v_{\text{L}}(t)=L{\frac {\mathrm {d} i_{\text{L}}(t)}{\mathrm {d} t}}}$

Esta vez, considerando que la señal actual es:

${\displaystyle i_{\text{L}}(t)=I_{p}\sin(\omega t)}$

resulta que:

${\displaystyle {\frac {\mathrm {d} i_{\text{L}}(t)}{\mathrm {d} t}}=\omega I_{p}\cos {\mathord {\left(\omega t\right)}}}$

Este resultado se expresa comúnmente en forma polar como

${\displaystyle Z_{\text{inductor}}=\omega Le^{j{\frac {\pi }{2}}}}$

o, utilizando la fórmula de Euler, como

${\displaystyle Z_{\text{inductor}}=j\omega L}$

Al igual que en el caso de los condensadores, también es posible derivar esta fórmula directamente de las representaciones complejas de los voltajes y corrientes, o suponiendo un voltaje sinusoidal entre los dos polos del inductor. En este último caso, la integración de la ecuación diferencial anterior conduce a un término constante para la corriente, que representa una polarización de CC fija que fluye a través del inductor. Este término se establece en cero porque el análisis de CA que utiliza la impedancia del dominio de frecuencia considera una frecuencia a la vez y la CC representa una frecuencia separada de cero hertz en este contexto.

La impedancia definida en términos de jω se puede aplicar estrictamente solo a circuitos que funcionan con una señal de CA de estado estable. El concepto de impedancia se puede extender a un circuito energizado con cualquier señal arbitraria utilizando una frecuencia compleja en lugar de jω . La frecuencia compleja se representa con el símbolo s y, en general, es un número complejo. Las señales se expresan en términos de frecuencia compleja tomando la transformada de Laplace de la expresión de dominio temporal de la señal. La impedancia de los elementos básicos del circuito en esta notación más general es la siguiente:

Elemento	Expresión de impedancia
Resistor	${\displaystyle R\,}$
Inductor	${\displaystyle sL\,}$
Condensador	${\displaystyle {\frac {1}{sC}}\,}$

Para un circuito de CC, esto se simplifica a s = 0. Para una señal de CA sinusoidal de estado estable, s = jω .

La impedancia de un componente eléctrico se define como la relación entre las transformadas de Laplace del voltaje sobre él y la corriente a través de él, es decir${\displaystyle Z}$

${\displaystyle Z(s)={\frac {{\mathcal {L}}\{v(t)\}}{{\mathcal {L}}\{i(t)\}}}={\frac {V(s)}{I(s)}}\qquad {\text{(general impedance)}}}$

donde es el parámetro complejo de Laplace. A modo de ejemplo, según la ley IV de un condensador, , de lo que se deduce que .${\displaystyle s=\sigma +j\omega }$${\displaystyle {\mathcal {L}}\{i(t)\}={\mathcal {L}}\{C\,\mathrm {d} v(t)/\mathrm {d} t\}=sC{\mathcal {L}}\{v(t)\}}$${\displaystyle Z_{C}(s)=1/sC}$

En el régimen fasorial (CA de estado estable, lo que significa que todas las señales se representan matemáticamente como exponenciales complejos simples y oscilan a una frecuencia común ), la impedancia se puede calcular simplemente como la relación voltaje-corriente, en la que el factor común dependiente del tiempo se cancela:${\displaystyle v(t)={\hat {V}}\,e^{j\omega t}}$${\displaystyle i(t)={\hat {I}}\,e^{j\omega t}}$${\displaystyle \omega }$

${\displaystyle Z(\omega )={\frac {v(t)}{i(t)}}={\frac {{\hat {V}}\,e^{j\omega t}}{{\hat {I}}\,e^{j\omega t}}}={\frac {\hat {V}}{\hat {I}}}\qquad {\text{(phasor-regime impedance)}}}$

Nuevamente, para un capacitor, se obtiene que , y por lo tanto . El dominio fasorial a veces se denomina dominio de frecuencia, aunque carece de una de las dimensiones del parámetro de Laplace. ^[17] Para CA en estado estable, la forma polar de la impedancia compleja relaciona la amplitud y la fase del voltaje y la corriente. En particular:${\displaystyle i(t)=C\,\mathrm {d} v(t)/\mathrm {d} t=j\omega C\,v(t)}$${\displaystyle Z_{C}(\omega )=1/j\omega C}$

• La magnitud de la impedancia compleja es la relación entre la amplitud del voltaje y la amplitud de la corriente;
• La fase de la impedancia compleja es el cambio de fase por el cual la corriente se retrasa respecto del voltaje.

Estas dos relaciones se mantienen incluso después de tomar la parte real de los exponenciales complejos (ver fasores ), que es la parte de la señal que uno realmente mide en los circuitos de la vida real.

La resistencia y la reactancia juntas determinan la magnitud y la fase de la impedancia a través de las siguientes relaciones:

${\displaystyle {\begin{aligned}|Z|&={\sqrt {ZZ^{*}}}={\sqrt {R^{2}+X^{2}}}\\\theta &=\arctan {\left({\frac {X}{R}}\right)}\end{aligned}}}$

En muchas aplicaciones, la fase relativa del voltaje y la corriente no es crítica, por lo que solo la magnitud de la impedancia es significativa.

La resistencia es la parte real de la impedancia; un dispositivo con una impedancia puramente resistiva no presenta ningún cambio de fase entre el voltaje y la corriente.${\displaystyle R}$

${\displaystyle \ R=|Z|\cos {\theta }\quad }$

La reactancia es la parte imaginaria de la impedancia; un componente con una reactancia finita induce un cambio de fase entre el voltaje a través de él y la corriente a través de él.${\displaystyle X}$${\displaystyle \theta }$

${\displaystyle \ X=|Z|\sin {\theta }\quad }$

Un componente puramente reactivo se distingue por el hecho de que la tensión sinusoidal que atraviesa el componente está en cuadratura con la corriente sinusoidal que lo atraviesa. Esto implica que el componente absorbe energía del circuito de forma alternada y luego la devuelve al circuito. Una reactancia pura no disipa ninguna potencia.

Un condensador tiene una impedancia puramente reactiva que es inversamente proporcional a la frecuencia de la señal . Un condensador consta de dos conductores separados por un aislante , también conocido como dieléctrico .

${\displaystyle X_{\mathsf {C}}={\frac {-1\ ~}{\ \omega \ C\ }}={\frac {-1\ ~}{\ 2\pi \ f\ C\ }}~.}$

El signo menos indica que la parte imaginaria de la impedancia es negativa.

A bajas frecuencias, un condensador se aproxima a un circuito abierto, por lo que no fluye corriente a través de él.

Un voltaje de CC aplicado a un capacitor hace que la carga se acumule en un lado; el campo eléctrico debido a la carga acumulada es la fuente de oposición a la corriente. Cuando el potencial asociado con la carga equilibra exactamente el voltaje aplicado, la corriente se vuelve cero.

Un condensador alimentado por una fuente de corriente alterna acumula solo una carga limitada antes de que la diferencia de potencial cambie de signo y la carga se disipe. Cuanto mayor sea la frecuencia, menos carga se acumula y menor es la oposición a la corriente.

La reactancia inductiva es proporcional a la frecuencia de la señal y a la inductancia .${\displaystyle X_{L}}$ ${\displaystyle f}$ ${\displaystyle L}$

${\displaystyle X_{L}=\omega L=2\pi fL\quad }$

Un inductor consiste en un conductor enrollado. La ley de inducción electromagnética de Faraday proporciona la fuerza contraelectromotriz (tensión opuesta a la corriente) debido a una tasa de cambio de la densidad de flujo magnético a través de un bucle de corriente.${\displaystyle {\mathcal {E}}}$ ${\displaystyle B}$

${\displaystyle {\mathcal {E}}=-{{d\Phi _{B}} \over dt}\quad }$

Para un inductor que consta de una bobina con bucles esto da:${\displaystyle N}$

${\displaystyle {\mathcal {E}}=-N{d\Phi _{B} \over dt}\quad }$

La fuerza contraelectromotriz es la fuente de la oposición al flujo de corriente. Una corriente continua constante tiene una tasa de cambio cero y ve un inductor como un cortocircuito (normalmente está hecho de un material con una resistividad baja ). Una corriente alterna tiene una tasa de cambio promediada en el tiempo que es proporcional a la frecuencia, lo que provoca el aumento de la reactancia inductiva con la frecuencia.

La reactancia total viene dada por

${\displaystyle {X=X_{L}+X_{C}}}$( es negativo)${\displaystyle X_{C}}$

de modo que la impedancia total es

${\displaystyle \ Z=R+jX}$

La impedancia total de muchas redes simples de componentes se puede calcular utilizando las reglas para combinar impedancias en serie y en paralelo. Las reglas son idénticas a las de combinación de resistencias, excepto que los números en general son números complejos . Sin embargo, el caso general requiere transformadas de impedancia equivalentes además de las de serie y paralelo.

Para los componentes conectados en serie, la corriente a través de cada elemento del circuito es la misma; la impedancia total es la suma de las impedancias de los componentes.

${\displaystyle \ Z_{\text{eq}}=Z_{1}+Z_{2}+\cdots +Z_{n}\quad }$

O explícitamente en términos reales e imaginarios:

${\displaystyle \ Z_{\text{eq}}=R+jX=(R_{1}+R_{2}+\cdots +R_{n})+j(X_{1}+X_{2}+\cdots +X_{n})\quad }$

Para los componentes conectados en paralelo, el voltaje en cada elemento del circuito es el mismo; la relación de las corrientes a través de dos elementos es la relación inversa de sus impedancias.

Por lo tanto, la impedancia total inversa es la suma de las inversas de las impedancias de los componentes:

${\displaystyle {\frac {1}{Z_{\text{eq}}}}={\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}+\cdots +{\frac {1}{Z_{n}}}}$

o, cuando n = 2:

${\displaystyle {\frac {1}{Z_{\text{eq}}}}={\frac {1}{Z_{1}}}+{\frac {1}{Z_{2}}}={\frac {Z_{1}+Z_{2}}{Z_{1}Z_{2}}}}$

${\displaystyle \ Z_{\text{eq}}={\frac {Z_{1}Z_{2}}{Z_{1}+Z_{2}}}}$

La impedancia equivalente se puede calcular en términos de la resistencia en serie equivalente y la reactancia . ^[18]${\displaystyle Z_{\text{eq}}}$${\displaystyle R_{\text{eq}}}$${\displaystyle X_{\text{eq}}}$

${\displaystyle {\begin{aligned}Z_{\text{eq}}&=R_{\text{eq}}+jX_{\text{eq}}\\R_{\text{eq}}&={\frac {(X_{1}R_{2}+X_{2}R_{1})(X_{1}+X_{2})+(R_{1}R_{2}-X_{1}X_{2})(R_{1}+R_{2})}{(R_{1}+R_{2})^{2}+(X_{1}+X_{2})^{2}}}\\X_{\text{eq}}&={\frac {(X_{1}R_{2}+X_{2}R_{1})(R_{1}+R_{2})-(R_{1}R_{2}-X_{1}X_{2})(X_{1}+X_{2})}{(R_{1}+R_{2})^{2}+(X_{1}+X_{2})^{2}}}\end{aligned}}}$

La medición de la impedancia de dispositivos y líneas de transmisión es un problema práctico en la tecnología de radio y otros campos. Las mediciones de impedancia se pueden realizar en una frecuencia, o puede ser de interés la variación de la impedancia del dispositivo en un rango de frecuencias. La impedancia se puede medir o visualizar directamente en ohmios, o se pueden visualizar otros valores relacionados con la impedancia; por ejemplo, en una antena de radio , la relación de onda estacionaria o el coeficiente de reflexión pueden ser más útiles que la impedancia sola. La medición de la impedancia requiere la medición de la magnitud del voltaje y la corriente, y la diferencia de fase entre ellos. La impedancia se mide a menudo mediante métodos de "puente" , similares al puente de Wheatstone de corriente continua ; se ajusta una impedancia de referencia calibrada para equilibrar el efecto de la impedancia del dispositivo bajo prueba. La medición de la impedancia en dispositivos electrónicos de potencia puede requerir la medición simultánea y el suministro de energía al dispositivo operativo.

La impedancia de un dispositivo se puede calcular mediante la división compleja del voltaje y la corriente. La impedancia del dispositivo se puede calcular aplicando un voltaje sinusoidal al dispositivo en serie con una resistencia y midiendo el voltaje a través de la resistencia y a través del dispositivo. Al realizar esta medición barriendo las frecuencias de la señal aplicada, se obtiene la fase y la magnitud de la impedancia. ^[19]

El uso de una respuesta de impulso se puede utilizar en combinación con la transformada rápida de Fourier (FFT) para medir rápidamente la impedancia eléctrica de varios dispositivos eléctricos. ^[19]

El medidor LCR (Inductancia (L), Capacitancia (C) y Resistencia (R)) es un dispositivo comúnmente utilizado para medir la inductancia, resistencia y capacitancia de un componente; a partir de estos valores, se puede calcular la impedancia en cualquier frecuencia.

Consideremos un circuito de tanque LC . La impedancia compleja del circuito es

${\displaystyle Z(\omega )={\frac {j\omega L}{1-\omega ^{2}LC}}.}$

Se ve inmediatamente que el valor de es mínimo (en realidad igual a 0 en este caso) siempre que ${\textstyle {1 \over |Z|}}$

${\displaystyle \omega ^{2}LC=1.}$

Por lo tanto, la frecuencia angular de resonancia fundamental es

${\displaystyle \omega ={1 \over {\sqrt {LC}}}.}$

En general, ni la impedancia ni la admitancia pueden variar con el tiempo, ya que se definen para exponenciales complejos en los que −∞ < t < +∞ . Si la relación de voltaje a corriente exponencial compleja cambia con el tiempo o la amplitud, el elemento del circuito no se puede describir utilizando el dominio de la frecuencia. Sin embargo, muchos componentes y sistemas (por ejemplo, varicaps que se utilizan en sintonizadores de radio ) pueden exhibir relaciones de voltaje a corriente no lineales o variables en el tiempo que parecen ser lineales invariantes en el tiempo (LTI) para señales pequeñas y sobre pequeñas ventanas de observación, por lo que se pueden describir aproximadamente como si tuvieran una impedancia variable en el tiempo. Esta descripción es una aproximación: sobre grandes oscilaciones de señal o amplias ventanas de observación, la relación de voltaje a corriente no será LTI y no se puede describir por impedancia.

• Análisis de impedancia bioeléctrica  : método para estimar la composición corporal
• Impedancia característica  – Propiedad de un circuito eléctrico
• Características eléctricas de los altavoces dinámicos
• Alta impedancia  : nodo en un circuito que restringe el flujo de corriente
• Inmitancia  : medida combinada de impedancia y admitancia.
• Analizador de impedancia  : tipo de equipo de prueba electrónico
• Puente de impedancia
• Cardiografía de impedancia  : técnica hemorreológica para detectar las propiedades del flujo sanguíneo en el tórax.Pages displaying wikidata descriptions as a fallback
• Control de impedancia
• Adaptación de impedancia  : ajuste de las impedancias de entrada/salida de un circuito eléctrico para algún propósito.
• Microbiología de impedancia
• Convertidor de impedancia negativa  : circuito activo que inyecta energía en los circuitos.
• Distancia de resistencia  : métrica gráfica de la resistencia eléctrica entre nodos
• Impedancia de la línea de transmisión
• Respuesta dieléctrica universal  : un comportamiento de escalamiento emergente en materiales heterogéneos bajo corriente alternaPages displaying wikidata descriptions as a fallback

• Kline, Ronald R., Steinmetz: ingeniero y socialista , Plunkett Lake Press, 2019 (reimpresión de libro electrónico de Johns Hopkins University Press, 1992 ISBN 9780801842986 ). 

• ECE 209: Revisión de circuitos como sistemas LTI – Breve explicación del análisis de circuitos en el dominio de Laplace; incluye una definición de impedancia.