Potencial eléctrico

Potencial eléctrico
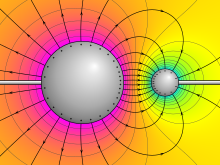Potencial eléctrico alrededor de dos esferas conductoras con cargas opuestas. El violeta representa el potencial más alto, el amarillo el cero y el cian el potencial más bajo. Las líneas de campo eléctrico se muestran perpendiculares a la superficie de cada esfera.
Símbolos comunes	V , φ
Unidad SI	voltio
Otras unidades	estatvoltio
En unidades básicas del SI	V = kg⋅m 2 ⋅s −3 ⋅A −1
¿ Extenso ?	Sí
Dimensión	ml 2 T −3 yo −1​

Artículos sobre
Electromagnetismo
Electricidad Magnetismo Óptica Historia Computacional Libros de texto Fenómenos
Electrostática Densidad de carga Conductor Ley de Coulomb Electreto Carga eléctrica Dipolo eléctrico Campo eléctrico Flujo eléctrico Potencial eléctrico Descarga electrostática Inducción electrostática Ley de Gauss Aislante Permitividad Polarización Energía potencial Electricidad estática Triboelectricidad
Magnetostática Ley de Ampère Ley de Biot-Savart Ley magnética de Gauss Dipolo magnético Campo magnético Flujo magnético Potencial escalar magnético Potencial vectorial magnético Magnetización Permeabilidad Regla de la mano derecha
Electrodinámica Radiación de frenado Radiación ciclotrónica Corriente de desplazamiento Corriente de Foucault Campo electromagnético Inducción electromagnética Pulso electromagnético Radiación electromagnética Ley de Faraday Ecuaciones de Jefimenko Fórmula de Larmor Ley de Lenz Potencial de Liénard-Wiechert Ecuaciones de Londres Fuerza de Lorentz Ecuaciones de Maxwell Tensor de Maxwell Vector de Poynting Radiación de sincrotrón
Red eléctrica Corriente alterna Capacidad Densidad de corriente Corriente continua Corriente eléctrica Energía eléctrica Electrólisis Fuerza electromotriz Impedancia Inductancia Calentamiento Joule Leyes de Kirchhoff Análisis de red Ley de Ohm Circuito paralelo Resistencia Cavidades resonantes Circuito en serie Voltaje Vatio Guías de ondas
Circuito magnético Motor de corriente alterna Motor de corriente continua Maquina electrica Motor eléctrico Gyrator–capacitor Induction motor Linear motor Magnetomotive force Permeance Reluctance (complex) Reluctance (real) Rotor Stator Transformer
Covariant formulation Electromagnetic tensor Electromagnetism and special relativity Four-current Four-potential Mathematical descriptions Maxwell equations in curved spacetime Relativistic electromagnetism Stress–energy tensor
Scientists Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Helmholtz Henry Hertz Hopkinson Jefimenko Joule Kelvin Kirchhoff Larmor Lenz Liénard Lorentz Maxwell Neumann Ohm Ørsted Poisson Poynting Ritchie Savart Singer Steinmetz Tesla Thomson Volta Weber Wiechert
v t e

El potencial eléctrico (también llamado potencial de campo eléctrico , caída de potencial, potencial electrostático ) se define como la cantidad de trabajo / energía necesaria por unidad de carga eléctrica para mover la carga desde un punto de referencia a un punto específico en un campo eléctrico. Más precisamente, el potencial eléctrico es la energía por unidad de carga para una carga de prueba que es tan pequeña que la perturbación del campo en consideración es insignificante. Se supone que el movimiento a través del campo se realiza con una aceleración insignificante, para evitar que la carga de prueba adquiera energía cinética o produzca radiación. Por definición, el potencial eléctrico en el punto de referencia es cero unidades. Normalmente, el punto de referencia es la Tierra o un punto en el infinito , aunque se puede utilizar cualquier punto.

En electrostática clásica , el campo electrostático es una cantidad vectorial expresada como el gradiente del potencial electrostático, que es una cantidad escalar denotada por V o, ocasionalmente , φ , ^[1] igual a la energía potencial eléctrica de cualquier partícula cargada en cualquier ubicación (medida en julios ) dividida por la carga de esa partícula (medida en culombios ). Al dividir la carga de la partícula se obtiene un cociente que es una propiedad del propio campo eléctrico. En resumen, un potencial eléctrico es la energía potencial eléctrica por unidad de carga.

Este valor se puede calcular en un campo eléctrico estático (invariante en el tiempo) o dinámico (variable en el tiempo) en un momento específico con la unidad julios por culombio (J⋅C ⁻¹ ) o voltio (V). Se supone que el potencial eléctrico en el infinito es cero.

En electrodinámica , cuando hay campos que varían con el tiempo, el campo eléctrico no se puede expresar solo como un potencial escalar . En cambio, el campo eléctrico se puede expresar tanto como el potencial eléctrico escalar como el potencial vectorial magnético . ^[2] El potencial eléctrico y el potencial vectorial magnético juntos forman un cuatrivector , de modo que los dos tipos de potencial se mezclan bajo las transformaciones de Lorentz .

En la práctica, el potencial eléctrico es una función continua en todo el espacio, porque una derivada espacial de un potencial eléctrico discontinuo produce un campo eléctrico de magnitud imposiblemente infinita. En particular, el potencial eléctrico debido a una carga puntual idealizada (proporcional a 1 ⁄ r , con r la distancia desde la carga puntual) es continuo en todo el espacio excepto en la ubicación de la carga puntual. Aunque el campo eléctrico no es continuo a través de una carga superficial idealizada , no es infinito en ningún punto. Por lo tanto, el potencial eléctrico es continuo a través de una carga superficial idealizada. Además, una línea de carga idealizada tiene potencial eléctrico (proporcional a ln( r ) , con r la distancia radial desde la línea de carga) es continuo en todas partes excepto en la línea de carga.

La mecánica clásica explora conceptos como fuerza , energía y potencial . ^[3] La fuerza y ​​la energía potencial están directamente relacionadas. Una fuerza neta que actúa sobre cualquier objeto hará que este se acelere . A medida que un objeto se mueve en la dirección de una fuerza que actúa sobre él, su energía potencial disminuye. Por ejemplo, la energía potencial gravitatoria de una bala de cañón en la cima de una colina es mayor que en la base de la colina. A medida que rueda cuesta abajo, su energía potencial disminuye y se traduce en movimiento: energía cinética .

Es posible definir el potencial de ciertos campos de fuerza de modo que la energía potencial de un objeto en ese campo dependa únicamente de la posición del objeto con respecto al campo. Dos de esos campos de fuerza son el campo gravitacional y el campo eléctrico (en ausencia de campos magnéticos variables en el tiempo). Dichos campos afectan a los objetos debido a las propiedades intrínsecas (por ejemplo, masa o carga) y las posiciones de los objetos.

Un objeto puede poseer una propiedad conocida como carga eléctrica . Dado que un campo eléctrico ejerce fuerza sobre un objeto cargado, si el objeto tiene una carga positiva, la fuerza estará en la dirección del vector del campo eléctrico en la ubicación de la carga; si la carga es negativa, la fuerza estará en la dirección opuesta.

La magnitud de la fuerza viene dada por la cantidad de carga multiplicada por la magnitud del vector del campo eléctrico,

$${\displaystyle |\mathbf {F} |=q|\mathbf {E} |.}$$

Un potencial eléctrico en un punto r en un campo eléctrico estático E está dado por la integral de línea

donde C es una trayectoria arbitraria desde algún punto de referencia fijo hasta r ; está determinada de forma única hasta una constante que se suma o se resta de la integral. En electrostática, la ecuación de Maxwell-Faraday revela que el rotacional es cero, lo que hace que el campo eléctrico sea conservativo . Por lo tanto, la integral de línea anterior no depende de la trayectoria específica C elegida, sino solo de sus puntos finales, lo que hace que esté bien definida en todas partes. El teorema del gradiente nos permite escribir:${\textstyle \nabla \times \mathbf {E} }$${\textstyle V_{\mathbf {E} }}$

Esto indica que el campo eléctrico apunta "cuesta abajo" hacia voltajes más bajos. Por la ley de Gauss , también se puede determinar que el potencial satisface la ecuación de Poisson :$${\displaystyle \mathbf {\nabla } \cdot \mathbf {E} =\mathbf {\nabla } \cdot \left(-\mathbf {\nabla } V_{\mathbf {E} }\right)=-\nabla ^{2}V_{\mathbf {E} }=\rho /\varepsilon _{0}}$$

donde ρ es la densidad de carga total y denota la divergencia .${\textstyle \mathbf {\nabla } \cdot }$

El concepto de potencial eléctrico está estrechamente relacionado con el de energía potencial . Una carga de prueba , q , tiene una energía potencial eléctrica , U _E , dada por

$${\displaystyle U_{\mathbf {E} }=q\,V.}$$

La energía potencial y, por tanto, también el potencial eléctrico, sólo se define hasta una constante aditiva: se debe elegir arbitrariamente una posición en la que la energía potencial y el potencial eléctrico sean cero.

Estas ecuaciones no se pueden utilizar si , es decir, en el caso de un campo eléctrico no conservativo (causado por un campo magnético cambiante ; véanse las ecuaciones de Maxwell ). La generalización del potencial eléctrico a este caso se describe en la sección § Generalización a la electrodinámica.${\textstyle \nabla \times \mathbf {E} \neq \mathbf {0} }$

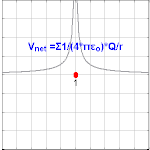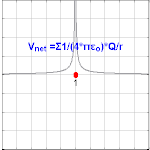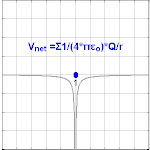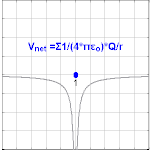
Se observa que el potencial eléctrico que surge de una carga puntual, Q , a una distancia, r , de la ubicación de Q es donde ε ₀ es la permitividad del vacío ^[4] , V _E se conoce como el potencial de Coulomb . Nótese que, en contraste con la magnitud de un campo eléctrico debido a una carga puntual, el potencial eléctrico escala con respecto al recíproco del radio, en lugar del radio al cuadrado.$${\displaystyle V_{\mathbf {E} }={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}},}$$

El potencial eléctrico en cualquier posición, r , en un sistema de cargas puntuales es igual a la suma de los potenciales eléctricos individuales debidos a cada carga puntual en el sistema. Este hecho simplifica los cálculos significativamente, porque la suma de campos potenciales (escalares) es mucho más fácil que la suma de campos eléctricos (vectoriales). Específicamente, el potencial de un conjunto de cargas puntuales discretas q _i en los puntos r _i se convierte en

$${\displaystyle V_{\mathbf {E} }(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\sum _{i=1}^{n}{\frac {q_{i}}{|\mathbf {r} -\mathbf {r} _{i}|}}\,}$$

dónde

• r es un punto en el que se evalúa el potencial;
• r _i es un punto en el que hay una carga distinta de cero; y
• q _i es la carga en el punto r _i .

Y el potencial de una distribución de carga continua ρ ( r ) se convierte en

$${\displaystyle V_{\mathbf {E} }(\mathbf {r} )={\frac {1}{4\pi \varepsilon _{0}}}\int _{R}{\frac {\rho (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}\mathrm {d} ^{3}r'\,,}$$

dónde

• r es un punto en el que se evalúa el potencial;
• R es una región que contiene todos los puntos en los que la densidad de carga es distinta de cero;
• r ' es un punto dentro de R ; y
• ρ ( r ' ) es la densidad de carga en el punto r ' .

Las ecuaciones dadas anteriormente para el potencial eléctrico (y todas las ecuaciones utilizadas aquí) están en las formas requeridas por las unidades del SI . En otros sistemas de unidades (menos comunes), como el CGS-Gaussiano , muchas de estas ecuaciones se verían alteradas.

Cuando hay campos magnéticos que varían en el tiempo (lo cual es cierto siempre que hay campos eléctricos que varían en el tiempo y viceversa), no es posible describir el campo eléctrico simplemente como un potencial escalar V porque el campo eléctrico ya no es conservativo : depende de la trayectoria porque (debido a la ecuación de Maxwell-Faraday ).${\displaystyle \textstyle \int _{C}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}}$${\displaystyle \mathbf {\nabla } \times \mathbf {E} \neq \mathbf {0} }$

En cambio, todavía se puede definir un potencial escalar incluyendo también el potencial vectorial magnético A . En particular, A se define para satisfacer:

$${\displaystyle \mathbf {B} =\mathbf {\nabla } \times \mathbf {A} }$$

donde B es el campo magnético . Por el teorema fundamental del cálculo vectorial , siempre se puede encontrar tal A , ya que la divergencia del campo magnético siempre es cero debido a la ausencia de monopolos magnéticos . Ahora, la cantidad es un campo conservativo, ya que el rotacional de se cancela por el rotacional de según la ecuación de Maxwell-Faraday . Por lo tanto, se puede escribir$${\displaystyle \mathbf {F} =\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}}$$${\displaystyle \mathbf {E} }$${\displaystyle {\frac {\partial \mathbf {A} }{\partial t}}}$$${\displaystyle \mathbf {E} =-\mathbf {\nabla } V-{\frac {\partial \mathbf {A} }{\partial t}},}$$

donde V es el potencial escalar definido por el campo conservativo F .

El potencial electrostático es simplemente el caso especial de esta definición donde A es invariante en el tiempo. Por otro lado, para campos que varían en el tiempo, a diferencia de la electrostática.$${\displaystyle -\int _{a}^{b}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\neq V_{(b)}-V_{(a)}}$$

Al potencial electrostático se le puede añadir cualquier constante sin afectar al campo eléctrico. En electrodinámica, el potencial eléctrico tiene infinitos grados de libertad. Para cualquier campo escalar (que puede variar en el tiempo o en el espacio), 𝜓 , podemos realizar la siguiente transformación de calibre para encontrar un nuevo conjunto de potenciales que produzcan exactamente los mismos campos eléctricos y magnéticos: ^[5]

$${\displaystyle {\begin{aligned}V^{\prime }&=V-{\frac {\partial \psi }{\partial t}}\\\mathbf {A} ^{\prime }&=\mathbf {A} +\nabla \psi \end{aligned}}}$$

Dadas distintas opciones de calibre, el potencial eléctrico podría tener propiedades muy diferentes. En el calibre de Coulomb , el potencial eléctrico viene dado por la ecuación de Poisson.

$${\displaystyle \nabla ^{2}V=-{\frac {\rho }{\varepsilon _{0}}}}$$

Al igual que en la electrostática, sin embargo, en el calibre de Lorenz , el potencial eléctrico es un potencial retardado que se propaga a la velocidad de la luz y es la solución de una ecuación de onda no homogénea :

$${\displaystyle \nabla ^{2}V-{\frac {1}{c^{2}}}{\frac {\partial ^{2}V}{\partial t^{2}}}=-{\frac {\rho }{\varepsilon _{0}}}}$$

La unidad de potencial eléctrico derivada del SI es el voltio (en honor a Alessandro Volta ), denotado como V, por lo que la diferencia de potencial eléctrico entre dos puntos en el espacio se conoce como voltaje . Las unidades más antiguas rara vez se utilizan hoy en día. Las variantes del sistema de unidades centímetro-gramo-segundo incluían varias unidades diferentes para el potencial eléctrico, entre ellas el abvoltio y el estatvoltio .

En el interior de los metales (y otros sólidos y líquidos), la energía de un electrón se ve afectada no solo por el potencial eléctrico, sino también por el entorno atómico específico en el que se encuentra. Cuando se conecta un voltímetro entre dos tipos diferentes de metal, mide la diferencia de potencial corregida para los diferentes entornos atómicos. ^[6] La cantidad medida por un voltímetro se llama potencial electroquímico o nivel de Fermi , mientras que el potencial eléctrico puro sin ajustar, V , a veces se llama potencial de Galvani , ϕ . Los términos "voltaje" y "potencial eléctrico" son un poco ambiguos, pero uno puede referirse a cualquiera de ellos en diferentes contextos.

Configuración de carga	Cifra	Potencial eléctrico
Alambre infinito		${\displaystyle V=-{\frac {\lambda }{2\pi \varepsilon _{0}}}\ln x,}$ donde es la densidad de carga lineal uniforme.${\displaystyle \lambda }$
Superficie infinitamente grande		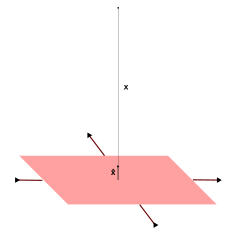${\displaystyle V=-{\frac {\sigma x}{2\varepsilon _{0}}},}$ donde es la densidad de carga superficial uniforme.${\displaystyle \sigma }$
Volumen cilíndrico infinitamente largo		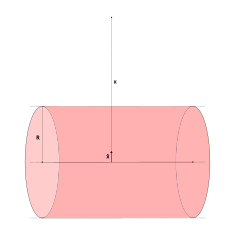${\displaystyle V=-{\frac {\lambda }{2\pi \varepsilon _{0}}}\ln x,}$ donde es la densidad de carga lineal uniforme.${\displaystyle \lambda }$
Volumen esférico		${\displaystyle V={\frac {Q}{4\pi \varepsilon _{0}x}},}$ fuera de la esfera, donde está la carga total distribuida uniformemente en el volumen.${\displaystyle Q}$	${\displaystyle V={\frac {Q(3R^{2}-r^{2})}{8\pi \varepsilon _{0}R^{3}}},}$ dentro de la esfera, donde está la carga total distribuida uniformemente en el volumen.${\displaystyle Q}$
Superficie esférica		${\displaystyle V={\frac {Q}{4\pi \varepsilon _{0}x}},}$ fuera de la esfera, donde está la carga total distribuida uniformemente en la superficie.${\displaystyle Q}$	${\displaystyle V={\frac {Q}{4\pi \varepsilon _{0}R}},}$ dentro de la esfera para una distribución uniforme de la carga.
Anillo cargado		${\displaystyle V={\frac {Q}{4\pi \varepsilon _{0}{\sqrt {R^{2}+x^{2}}}}},}$ en el eje, donde está la carga total distribuida uniformemente en el anillo.${\displaystyle Q}$
Disco cargado		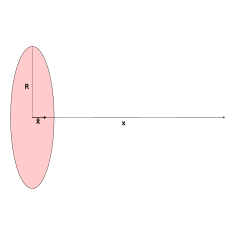${\displaystyle V={\frac {\sigma }{2\varepsilon _{0}}}\left[{\sqrt {x^{2}+R^{2}}}-x\right],}$ en el eje, donde es la densidad de carga superficial uniforme.${\displaystyle \sigma }$
Dipolo eléctrico		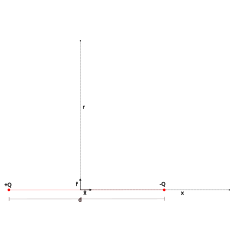${\displaystyle V=0,}$ en el plano ecuatorial.	${\displaystyle V={\frac {p}{4\pi \varepsilon _{0}x^{2}}},}$ en el eje (dado que ), donde también puede ser negativo para indicar la posición en la dirección opuesta en el eje, y es la magnitud del momento dipolar eléctrico .${\displaystyle x\gg d}$${\displaystyle x}$${\displaystyle p}$

• Potencial absoluto del electrodo
• Potencial electroquímico
• Potencial de electrodo

Wikimedia Commons alberga una categoría multimedia sobre Potencial eléctrico .