Teoría VSEPR
Modelo para predecir la geometría molecular
Ejemplo de disposición de electrones doblados (molécula de agua). Muestra la ubicación de los electrones desapareados, los átomos enlazados y los ángulos de enlace. El ángulo de enlace del agua es de 104,5°.

La teoría de repulsión de pares de electrones de la capa de valencia ( VSEPR ) ( / ˈ v ɛ s p ər , v ə ˈ s ɛ p ər / VESP -ər , [1] : 410  və- SEP -ər [2] ) es un modelo utilizado en química para predecir la geometría de moléculas individuales a partir del número de pares de electrones que rodean sus átomos centrales. [3] También se denomina teoría de Gillespie-Nyholm en honor a sus dos desarrolladores principales, Ronald Gillespie y Ronald Nyholm .

La premisa de la RPECV es que los pares de electrones de valencia que rodean a un átomo tienden a repelerse entre sí. Cuanto mayor sea la repulsión, mayor será la energía (menos estable) de la molécula. Por lo tanto, la geometría molecular predicha por la RPECV de una molécula es la que tiene la menor cantidad posible de esta repulsión. Gillespie ha enfatizado que la repulsión electrón-electrón debido al principio de exclusión de Pauli es más importante para determinar la geometría molecular que la repulsión electrostática . [4]

Los conocimientos de la teoría VSEPR se derivan del análisis topológico de la densidad electrónica de las moléculas. Estos métodos de topología química cuántica (QCT) incluyen la función de localización electrónica (ELF) y la teoría cuántica de átomos en moléculas (AIM o QTAIM). [4] [5]

Historia

La idea de una correlación entre la geometría molecular y el número de pares de electrones de valencia (tanto pares compartidos como no compartidos) fue propuesta originalmente en 1939 por Ryutaro Tsuchida en Japón, [6] y fue presentada de forma independiente en una Conferencia Bakerian en 1940 por Nevil Sidgwick y Herbert Powell de la Universidad de Oxford . [7] En 1957, Ronald Gillespie y Ronald Sydney Nyholm del University College de Londres refinaron este concepto en una teoría más detallada, capaz de elegir entre varias geometrías alternativas. [8] [9]

Descripción general

La teoría VSEPR se utiliza para predecir la disposición de pares de electrones alrededor de átomos centrales en moléculas, especialmente moléculas simples y simétricas. Un átomo central se define en esta teoría como un átomo que está unido a dos o más átomos, mientras que un átomo terminal está unido solo a otro átomo. [1] : 398  Por ejemplo, en la molécula de isocianato de metilo (H 3 C-N=C=O), los dos carbonos y un nitrógeno son átomos centrales, y los tres hidrógenos y un oxígeno son átomos terminales. [1] : 416  La geometría de los átomos centrales y sus pares de electrones no enlazantes determinan a su vez la geometría de la molécula completa más grande.

El número de pares de electrones en la capa de valencia de un átomo central se determina después de dibujar la estructura de Lewis de la molécula y expandirla para mostrar todos los grupos de enlace y pares solitarios de electrones. [1] : 410–417  En la teoría VSEPR, un enlace doble o triple se trata como un grupo de enlace simple. [1] La suma del número de átomos unidos a un átomo central y el número de pares solitarios formados por sus electrones de valencia no enlazantes se conoce como número estérico del átomo central.

Se supone que los pares de electrones (o grupos si hay enlaces múltiples) se encuentran en la superficie de una esfera centrada en el átomo central y tienden a ocupar posiciones que minimizan sus repulsiones mutuas al maximizar la distancia entre ellos. [1] : 410–417  [10] Por lo tanto, el número de pares de electrones (o grupos) determina la geometría general que adoptarán. Por ejemplo, cuando hay dos pares de electrones que rodean al átomo central, su repulsión mutua es mínima cuando se encuentran en polos opuestos de la esfera. Por lo tanto, se predice que el átomo central adoptará una geometría lineal . Si hay 3 pares de electrones que rodean al átomo central, su repulsión se minimiza al colocarlos en los vértices de un triángulo equilátero centrado en el átomo. Por lo tanto, la geometría predicha es trigonal . Del mismo modo, para 4 pares de electrones, la disposición óptima es tetraédrica . [1] : 410–417 

Como herramienta para predecir la geometría adoptada con un número dado de pares de electrones, una demostración física que se utiliza a menudo para demostrar el principio de repulsión mínima de pares de electrones es la utilización de globos inflados. Mediante la manipulación, los globos adquieren una ligera carga electrostática superficial que da lugar a la adopción de aproximadamente las mismas geometrías cuando se los ata por sus vástagos que el número correspondiente de pares de electrones. Por ejemplo, cinco globos atados entre sí adoptan la geometría bipiramidal trigonal , al igual que los cinco pares de enlaces de una molécula de PCl 5 .

Número estérico

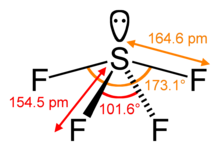
El tetrafluoruro de azufre tiene un número estérico de 5.

El número estérico de un átomo central en una molécula es el número de átomos unidos a ese átomo central, llamado su número de coordinación , más el número de pares solitarios de electrones de valencia en el átomo central. [11] En la molécula SF 4 , por ejemplo, el átomo central de azufre tiene cuatro ligandos ; el número de coordinación del azufre es cuatro. Además de los cuatro ligandos, el azufre también tiene un par solitario en esta molécula. Por lo tanto, el número estérico es 4 + 1 = 5.

Grado de repulsión

La geometría general se refina aún más al distinguir entre pares de electrones enlazantes y no enlazantes . El par de electrones enlazante compartido en un enlace sigma con un átomo adyacente se encuentra más alejado del átomo central que un par no enlazante (solitario) de ese átomo, que se mantiene cerca de su núcleo cargado positivamente. Por lo tanto, la teoría VSEPR considera que la repulsión por el par solitario es mayor que la repulsión por un par enlazante. Como tal, cuando una molécula tiene 2 interacciones con diferentes grados de repulsión, la teoría VSEPR predice la estructura donde los pares solitarios ocupan posiciones que les permiten experimentar menos repulsión. Las repulsiones par solitario-par solitario (lp-lp) se consideran más fuertes que las repulsiones par solitario-par enlazante (lp-bp), que a su vez se consideran más fuertes que las repulsiones par enlazante-par enlazante (bp-bp), distinciones que luego guían las decisiones sobre la geometría general cuando son posibles 2 o más posiciones no equivalentes. [1] : 410–417  Por ejemplo, cuando 5 pares de electrones de valencia rodean un átomo central, adoptan una geometría molecular bipiramidal trigonal con dos posiciones axiales colineales y tres posiciones ecuatoriales . Un par de electrones en posición axial tiene tres vecinos ecuatoriales cercanos a solo 90° de distancia y un cuarto mucho más lejos a 180°, mientras que un par de electrones ecuatorial tiene solo dos pares adyacentes a 90° y dos a 120°. La repulsión de los vecinos cercanos a 90° es más importante, de modo que las posiciones axiales experimentan más repulsión que las posiciones ecuatoriales; por lo tanto, cuando hay pares solitarios, tienden a ocupar posiciones ecuatoriales como se muestra en los diagramas de la siguiente sección para el número estérico cinco. [10]

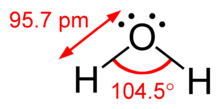
La diferencia entre pares solitarios y pares enlazantes también puede utilizarse para racionalizar las desviaciones de las geometrías idealizadas. Por ejemplo, la molécula de H 2 O tiene cuatro pares de electrones en su capa de valencia: dos pares solitarios y dos pares enlazantes. Los cuatro pares de electrones están distribuidos de forma que apuntan aproximadamente hacia los vértices de un tetraedro. Sin embargo, el ángulo de enlace entre los dos enlaces O–H es de sólo 104,5°, en lugar de los 109,5° de un tetraedro regular, porque los dos pares solitarios (cuyas envolventes de densidad o probabilidad se encuentran más cerca del núcleo del oxígeno) ejercen una mayor repulsión mutua que los dos pares enlazantes. [1] : 410–417  [10]

Un enlace de orden de enlace superior también ejerce mayor repulsión, ya que los electrones del enlace pi contribuyen. [10] Por ejemplo, en el isobutileno , (H 3 C) 2 C=CH 2 , el ángulo H 3 C−C=C (124°) es mayor que el ángulo H 3 C−C−CH 3 (111,5°). Sin embargo, en el ion carbonato , CO2−
3Los tres enlaces C−O son equivalentes con ángulos de 120° debido a la resonancia .

Método AXE

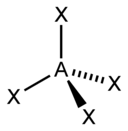
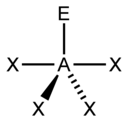
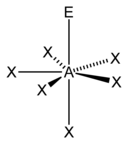
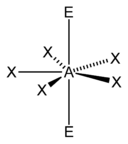
El "método AXE" de conteo de electrones se utiliza comúnmente cuando se aplica la teoría VSEPR. Los pares de electrones alrededor de un átomo central se representan mediante una fórmula AX m E n , donde A representa el átomo central y siempre tiene un subíndice implícito uno. Cada X representa un ligando (un átomo unido a A). Cada E representa un par solitario de electrones en el átomo central. [1] : 410–417  El número total de X y E se conoce como número estérico. Por ejemplo, en una molécula AX 3 E 2 , el átomo A tiene un número estérico de 5.

Cuando los átomos sustituyentes (X) no son todos iguales, la geometría sigue siendo aproximadamente válida, pero los ángulos de enlace pueden ser ligeramente diferentes de aquellos en los que todos los átomos externos son iguales. Por ejemplo, los carbonos de doble enlace en alquenos como C 2 H 4 son AX 3 E 0 , pero los ángulos de enlace no son todos exactamente 120°. Del mismo modo, SOCl 2 es AX 3 E 1 , pero debido a que los sustituyentes X no son idénticos, los ángulos X–A–X no son todos iguales.

Basándose en el número estérico y la distribución de X y E , la teoría VSEPR hace las predicciones de las siguientes tablas.

Elementos del grupo principal

En el caso de los elementos del grupo principal , existen pares solitarios estereoquímicamente activos E cuyo número puede variar entre 0 y 3. Nótese que las geometrías se nombran de acuerdo con las posiciones atómicas únicamente y no con la disposición de los electrones. Por ejemplo, la descripción de AX 2 E 1 como una molécula doblada significa que los tres átomos AX 2 no están en una línea recta, aunque el par solitario ayuda a determinar la geometría.


Número estérico		Geometría molecular [12]
0 pares solitarios		Geometría molecular [1] : 413–414 
1 par solitario		Geometría molecular [1] : 413–414 
2 pares solitarios		Geometría molecular [1] : 413–414 
3 pares solitarios
2
Lineal
   
3
Trigonal plana
Doblado
  
4
Tetraédrico
Pirámide trigonal
Doblado
 
5
Bipiramidal trigonal
Balancín
En forma de T
Lineal
6
Octaédrico
Pirámide cuadrada
Plano cuadrado
 
7
Bipiramidal pentagonal
Pirámide pentagonal
Planar pentagonal
 
8
Antiprismático cuadrado

 		  

Tipo de molécula		Forma molecular [1] : 413–414 Disposición electrónica [1] : 413–414 
, incluidos pares solitarios, que se muestran en amarillo		Geometría [1] : 413–414 
excluyendo pares solitarios		Ejemplos
Eje 2 E 0LinealBeCl2 , [ 3] CO2 [ 10]
Eje 2 E 1DobladoNO−
2, [3] SO 2 , [1] : 413–414  O 3 , [3] CCl 2
Eje 2 E 2Doblado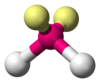H2O , [1] : 413–414  OF2 [ 13 ] : 448 
Eje 2 y 3LinealXeF 2 , [1] : 413–414  I−
3, [13] : 483  XeCl2
Eje 3 E 0Trigonal planaBF 3 , [1] : 413–414  CO2−
3, [13] : 368  CH
2Oh , no−
3, [3] SO 3 [10]
Eje 3 E 1Pirámide trigonalNH3 , [1] : 413–414  PCl3 [ 13 ] : 407 
Eje 3 y 2En forma de TClF3 , [1] : 413–414  BrF3 [ 13 ] : 481 
Eje 4 E 0Tetraédrico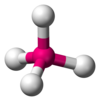Capítulo 4 , [1] : 413–414  PO3−
4, ENTONCES2−
4, [10] ClO−
4, [ 3] XeO4 [13] : 499 
Eje 4 E 1Balancín o diesfenoidal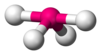SF 4 [1] : 413–414  [13] : 45 
Eje 4 E 2Plano cuadradoXeF 4 [1] : 413–414 
Eje 5 E 0Bipiramidal trigonalPCl5 , [1] : 413–414  PF5 , [ 1 ] : 413–414 
Eje 5 E 1Pirámide cuadrada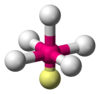ClF 5 , [13] : 481  BrF 5 , [1] : 413–414  XeOF 4 [10]
Eje 5 E 2Planar pentagonalXeF−
5[13] : 498 
Eje 6 E 0Octaédrico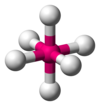SF 6 [1] : 413–414 
Eje 6 E 1Pirámide pentagonalXeOF−
5, [14] OIF2−
5[14]
Eje 7 E 0Bipiramidal pentagonal [10]SI 7 [10]
Eje 8 E 0Antiprismático cuadrado [10]SI−
8, XeF 8 2- en (NO) 2 XeF 8

Metales de transición (modelo Kepert)

Los pares solitarios en los átomos de metales de transición son usualmente estereoquímicamente inactivos, lo que significa que su presencia no cambia la geometría molecular. Por ejemplo, los complejos hexaaquo M(H 2 O) 6 son todos octaédricos para M = V 3+ , Mn 3+ , Co 3+ , Ni 2+ y Zn 2+ , a pesar del hecho de que las configuraciones electrónicas del ion metálico central son d 2 , d 4 , d 6 , d 8 y d 10 respectivamente. [13] : 542  El modelo de Kepert ignora todos los pares solitarios en átomos de metales de transición, de modo que la geometría alrededor de todos esos átomos corresponde a la geometría VSEPR para AX n con 0 pares solitarios E. [15] [13] : 542  Esto a menudo se escribe ML n , donde M = metal y L = ligando. El modelo de Kepert predice las siguientes geometrías para números de coordinación de 2 a 9:


Tipo de molécula		FormaGeometríaEjemplos
Ml 2LinealHgCl2 [3 ]
Ml 3Trigonal plana
ml 4TetraédricoNiCl2−
4
ml 5Bipiramidal trigonalFe(CO)
5
Pirámide cuadradaMnCl52−​​
ML6​OctaédricoWCl6 [ 13 ] : 659 
ML7​Bipiramidal pentagonal [10]ZrF3−
7
Octaédrico con capuchónMinisterio de Finanzas−
7
Prismático trigonal con tapa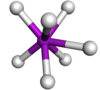TaF2−
7
ML8​Antiprismático cuadrado [10]Árbitro−
8
DodecaédricoMo(CN)4−
8
Prismático trigonal bicapeado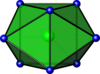ZrF4−
8
ML9​Prismático trigonal tricoplado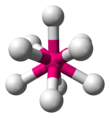ReH2−
9[13] : 254 
Cuadrado antiprismático con tapa

Ejemplos

La molécula de metano (CH 4 ) es tetraédrica porque tiene cuatro pares de electrones. Los cuatro átomos de hidrógeno están ubicados en los vértices de un tetraedro y el ángulo de enlace es cos −1 (− 1 ⁄ 3 ) ≈ 109° 28′. [16] [17] Esto se conoce como una molécula de tipo AX 4 . Como se mencionó anteriormente, A representa el átomo central y X representa un átomo externo. [1] : 410–417 

La molécula de amoniaco (NH 3 ) tiene tres pares de electrones involucrados en la unión, pero hay un par solitario de electrones en el átomo de nitrógeno. [1] : 392–393  No está enlazado con otro átomo; sin embargo, influye en la forma general a través de repulsiones. Al igual que en el metano anterior, hay cuatro regiones de densidad electrónica. Por lo tanto, la orientación general de las regiones de densidad electrónica es tetraédrica. Por otro lado, solo hay tres átomos externos. Esto se conoce como una molécula de tipo AX 3 E porque el par solitario está representado por una E. [1] : 410–417  Por definición, la forma o geometría molecular describe solo la disposición geométrica de los núcleos atómicos, que es trigonal-piramidal para NH 3 . [1] : 410–417 

Son posibles números estéricos de 7 o mayores, pero son menos comunes. El número estérico de 7 se presenta en el heptafluoruro de yodo (IF 7 ); la geometría base para un número estérico de 7 es bipiramidal pentagonal. [10] La geometría más común para un número estérico de 8 es una geometría antiprismática cuadrada . [18] : 1165  Ejemplos de esto incluyen el octacianomolibdato ( Mo(CN)4−
8) y octafluorocirconato ( ZrF4−
8) aniones. [18] : 1165  El ion nonahidrurohenato ( ReH2−
9) en nonahidruro de potasio es un ejemplo raro de un compuesto con un número estérico de 9, que tiene una geometría prismática trigonal tricapada. [13] : 254  [18]

Los números estéricos superiores a 9 son muy raros y no está claro qué geometría se prefiere generalmente. [19] Las posibles geometrías para números estéricos de 10, 11, 12 o 14 son antiprismático cuadrado bicapipado (o dodecadeltahédrico bicapipado ), octadecaédrico , icosaédrico y antiprismático hexagonal bicapipado , respectivamente. No existen compuestos con números estéricos tan altos que involucren ligandos monodentados , y aquellos que involucran ligandos multidentados a menudo se pueden analizar de manera más simple como complejos con números estéricos más bajos cuando algunos ligandos multidentados se tratan como una unidad. [18] : 1165, 1721 

Excepciones

Hay grupos de compuestos en los que la ecuación VSEPR no logra predecir la geometría correcta.

Algunos AX2mi0Moléculas

Se ha calculado que las formas de los análogos de alquinos de elementos más pesados ​​del Grupo 14 (RM≡MR, donde M = Si, Ge, Sn o Pb) están dobladas. [20] [21] [22]

Algunos AX2mi2Moléculas

Un ejemplo de la geometría AX 2 E 2 es el óxido de litio molecular , Li 2 O, una estructura lineal en lugar de curvada, que se atribuye a que sus enlaces son esencialmente iónicos y la fuerte repulsión litio-litio resultante. [23] Otro ejemplo es O(SiH 3 ) 2 con un ángulo Si–O–Si de 144,1°, que se compara con los ángulos en Cl 2 O (110,9°), (CH 3 ) 2 O (111,7°) y N(CH 3 ) 3 (110,9°). [24] Gillespie y Robinson racionalizan el ángulo de enlace Si–O–Si basándose en la capacidad observada del par solitario de un ligando para repeler en gran medida otros pares de electrones cuando la electronegatividad del ligando es mayor o igual que la del átomo central. [24] En O(SiH 3 ) 2 , el átomo central es más electronegativo y los pares solitarios están menos localizados y son más débilmente repulsivos. El mayor ángulo de enlace Si–O–Si resulta de esto y de la fuerte repulsión ligando-ligando por el ligando -SiH 3 relativamente grande . [24] Burford et al. demostraron a través de estudios de difracción de rayos X que Cl 3 Al–O–PCl 3 tiene un ángulo de enlace Al–O–P lineal y, por lo tanto, es una molécula no VSEPR. [25]

Algunos AX6mi1y AX8mi1Moléculas

Hexafluoruro de xenón , que tiene una geometría octaédrica distorsionada

Algunas moléculas de AX 6 E 1 , por ejemplo, hexafluoruro de xenón (XeF 6 ) y los aniones Te(IV) y Bi(III), TeCl2−
6, TeBr2−
6, BiCl3−
6, BiBr3−
6y BiI3−
6, son pirámides octaédricas, en lugar de pentagonales, y el par solitario no afecta la geometría en el grado predicho por la RPECV. [26] De manera similar, el ion octafluoroxenato ( XeF2−
8) en octafluoroxenato de nitrosonio(VI) [13] : 498  [27] [28] es un antiprisma cuadrado con una distorsión mínima, a pesar de tener un par solitario. Una racionalización es que el hacinamiento estérico de los ligandos deja poco o ningún espacio para el par solitario no enlazante; [24] otra racionalización es el efecto del par inerte . [13] : 214 

ML plana cuadrada4complejos

El modelo de Kepert predice que las moléculas del metal de transición ML 4 tienen forma tetraédrica y no puede explicar la formación de complejos planos cuadrados. [13] : 542  La mayoría de estos complejos exhiben una configuración ad 8 como en el caso del tetracloroplatinato ( PtCl2−
4) ion. La explicación de la forma de los complejos planos cuadrados implica efectos electrónicos y requiere el uso de la teoría de campos cristalinos . [13] : 562–4 

Complejos con fuerte contribución d

Hexametiltungsteno , un complejo de metal de transición cuya geometría es diferente de la del grupo principal de coordinación.

Algunos complejos de metales de transición con un bajo conteo de electrones d tienen geometrías inusuales, que pueden atribuirse a la interacción de enlace de la subcapa d. [29] Gillespie descubrió que esta interacción produce pares de enlace que también ocupan los respectivos puntos antípodas (ligando opuesto) de la esfera. [30] [4] Este fenómeno es un efecto electrónico que resulta de la forma bilobulada de los orbitales híbridos sd x subyacentes . [31] [32] La repulsión de estos pares de enlace conduce a un conjunto diferente de formas.

Tipo de moléculaFormaGeometríaEjemplos
Ml 2DobladoTiO2 [29 ]
Ml 3Pirámide trigonalCromo3 [33 ]
ml 4TetraédricoTiCl4 [ 13 ] : 598–599 
ml 5Pirámide cuadradaTa(CH3 ) 5 [ 34]
ML6​C 3v Prismático trigonalW(CH3 ) 6 [ 35]

Las estructuras en fase gaseosa de los haluros triatómicos de los miembros más pesados ​​del grupo 2 (es decir, haluros de calcio, estroncio y bario, MX 2 ), no son lineales como se predijo, sino que están curvadas (ángulos X–M–X aproximados: CaF 2 , 145°; SrF 2 , 120°; BaF 2 , 108°; SrCl 2 , 130°; BaCl 2 , 115°; BaBr 2 , 115°; BaI 2 , 105°). [36] Gillespie ha propuesto que esto también es causado por la interacción de enlace de los ligandos con la subcapa d del átomo de metal, influyendo así en la geometría molecular. [24] [37]

Elementos superpesados

Se predice que los efectos relativistas en los orbitales electrónicos de los elementos superpesados ​​influirán en la geometría molecular de algunos compuestos. Por ejemplo, los electrones 6d 5/2 en el nihonio juegan un papel inesperadamente fuerte en la unión, por lo que el NhF 3 debería asumir una geometría en forma de T, en lugar de una geometría plana trigonal como su congénere más ligero BF 3 . [38] En contraste, se predice que la estabilidad adicional de los electrones 7p 1/2 en la tenesina hará que el TsF 3 sea trigonal plano, a diferencia de la geometría en forma de T observada para el IF 3 y predicha para el At F 3 ; [39] de manera similar, el Og F 4 debería tener una geometría tetraédrica, mientras que el XeF 4 tiene una geometría plana cuadrada y se predice que el Rn F 4 tendrá la misma. [40]

Moléculas con electrones impares

La teoría VSEPR se puede extender a moléculas con un número impar de electrones al tratar al electrón desapareado como un "medio par de electrones"; por ejemplo, Gillespie y Nyholm [8] : 364-365  sugirieron que la disminución del ángulo de enlace en la serie NO+
2(180°), NO 2 (134°), NO−
2(115°) indica que un conjunto dado de pares de electrones enlazantes ejerce una repulsión más débil sobre un único electrón no enlazante que sobre un par de electrones no enlazantes. En efecto, consideraron al dióxido de nitrógeno como una molécula AX 2 E 0,5 , con una geometría intermedia entre NO+
2y NO−
2De manera similar, el dióxido de cloro (ClO 2 ) es una molécula AX 2 E 1,5 , con una geometría intermedia entre ClO+
2y ClO−
2. [ cita requerida ]

Finalmente, se predice que el radical metilo (CH 3 ) es piramidal trigonal como el anión metilo ( CH−
3), pero con un ángulo de enlace mayor (como en el catión metilo trigonal planar ( CH+
3)). Sin embargo, en este caso, la predicción VSEPR no es del todo cierta, ya que el CH 3 es en realidad planar, aunque su distorsión a una geometría piramidal requiere muy poca energía. [41]

Véase también

Referencias

  1. ^ abcdefghijklmnopqrstu vwxyz aa ab ac ad ae af ag Petrucci, RH; WS, Harwood; FG, Herring (2002). Química general: principios y aplicaciones modernas (8.ª ed.). Prentice-Hall. ISBN 978-0-13-014329-7.
  2. ^ Stoker, H. Stephen (2009). Química general, orgánica y biológica . Cengage Learning. pág. 119. ISBN 978-0-547-15281-3.
  3. ^ abcdefg Jolly, WL (1984). Química inorgánica moderna. McGraw-Hill. págs. 77–90. ISBN 978-0-07-032760-3.
  4. ^ abc Gillespie, RJ (2008). "Cincuenta años del modelo VSEPR". Coord. Chem. Rev. 252 ( 12–14): 1315–1327. doi :10.1016/j.ccr.2007.07.007.
  5. ^ Bader, Richard FW; Gillespie, Ronald J.; MacDougall, Preston J. (1988). "Una base física para el modelo VSEPR de geometría molecular". J. Am. Chem. Soc . 110 (22): 7329–7336. doi :10.1021/ja00230a009.
  6. ^ Tsuchida, Ryutaro (1939). "Una nueva teoría simple de la valencia" 新簡易原子價論 [Nueva teoría de la valencia simple]. Nippon Kagaku Kaishi (en japonés). 60 (3): 245–256. doi : 10.1246/nikkashi1921.60.245 .
  7. ^ Sidgwick, NV; Powell, HM (1940). "Bakerian Lecture. Stereochemical Types and Valencia Groups". Proc. R. Soc. A . 176 (965): 153–180. Código Bibliográfico :1940RSPSA.176..153S. doi : 10.1098/rspa.1940.0084 .
  8. ^ ab Gillespie, RJ ; Nyholm, RS (1957). "Estereoquímica inorgánica". Q. Rev. Chem. Soc . 11 (4): 339. doi :10.1039/QR9571100339.
  9. ^ Gillespie, RJ (1970). "El modelo de repulsión de pares de electrones para la geometría molecular". J. Chem. Educ . 47 (1): 18. Bibcode :1970JChEd..47...18G. doi :10.1021/ed047p18.
  10. ^ abcdefghijklmn Miessler, GL; Tarr, DA (1999). Química inorgánica (2.ª ed.). Prentice-Hall. págs. 54–62. ISBN 978-0-13-841891-5.
  11. ^ Miessler, GL; Tarr, DA (1999). Química inorgánica (2.ª ed.). Prentice-Hall. pág. 55. ISBN 978-0-13-841891-5.
  12. ^ Petrucci, RH; WS, Harwood; FG, Herring (2002). Química general: principios y aplicaciones modernas (8.ª ed.). Prentice-Hall. pp. 413–414 (Tabla 11.1). ISBN 978-0-13-014329-7.
  13. ^ abcdefghijklmnopqrs Housecroft, CE; Sharpe, AG (2005). Química inorgánica (2.ª ed.). Pearson. ISBN 978-0-130-39913-7.
  14. ^ ab Baran, E. (2000). "Amplitudes medias de vibración de la pirámide pentagonal XeOF−
    5    y la OIF2−
    5    aniones". J. Fluorine Chem . 101 : 61–63. doi :10.1016/S0022-1139(99)00194-3.
  15. ^ Anderson, OP (1983). "Reseñas de libros: Estereoquímica inorgánica (por David L. Kepert)" (PDF) . Acta Crystallographica B. 39 : 527–528. doi : 10.1107/S0108768183002864 . Consultado el 14 de septiembre de 2020. basado en una aplicación cuantitativa sistemática de las ideas comunes sobre la repulsión de pares de electrones .
  16. ^ Brittin, WE (1945). "Ángulo de valencia del átomo de carbono tetraédrico". J. Chem. Educ . 22 (3): 145. Código Bibliográfico :1945JChEd..22..145B. doi :10.1021/ed022p145.
  17. ^ "Ángulo entre dos patas de un tetraedro" Archivado el 3 de octubre de 2018 en Wayback Machine – Maze5.net
  18. ^ abcd Wiberg, E.; Holleman, AF (2001). Química inorgánica . Academic Press. ISBN 978-0-12-352651-9.
  19. ^ Wulfsberg, Gary (2000). Química inorgánica . University Science Books. pág. 107. ISBN 9781891389016.
  20. ^ Power, Philip P. (septiembre de 2003). "Análogos de acetilenos de silicio, germanio, estaño y plomo". Chem. Commun. (17): 2091–2101. doi :10.1039/B212224C. PMID  13678155.
  21. ^ Nagase, Shigeru; Kobayashi, Kaoru; Takagi, Nozomi (6 de octubre de 2000). "Triples enlaces entre elementos más pesados ​​del grupo 14. Un enfoque teórico". J. Organomet. Chem. 11 (1–2): 264–271. doi :10.1016/S0022-328X(00)00489-7.
  22. ^ Sekiguchi, Akira; Kinjō, Rei; Ichinohe, Masaaki (septiembre de 2004). "Un compuesto estable que contiene un triple enlace silicio-silicio" (PDF) . Ciencia . 305 (5691): 1755-1757. Código bibliográfico : 2004 Ciencia... 305.1755S. doi :10.1126/ciencia.1102209. PMID  15375262. S2CID  24416825.[ enlace muerto permanente ]
  23. ^ Bellert, D.; Breckenridge, WH (2001). "Una determinación espectroscópica de la longitud de enlace de la molécula de LiOLi: fuerte enlace iónico". J. Chem. Phys. 114 (7): 2871. Bibcode :2001JChPh.114.2871B. doi :10.1063/1.1349424.
  24. ^ abcde Gillespie, RJ; Robinson, EA (2005). "Modelos de geometría molecular". Chem. Soc. Rev. 34 (5): 396–407. doi :10.1039/b405359c. PMID  15852152.
  25. ^ Burford, Neil; Phillips, Andrew; Schurko, Robert; Wasylishen, Roderick; Richardson, John (1997). "Aislamiento y caracterización integral del estado sólido de Cl3Al–O–PCl3". Chemical Communications . 1997 (24): 2363–2364 . Consultado el 3 de abril de 2024 .
  26. ^ Wells, AF (1984). Química inorgánica estructural (5.ª ed.). Oxford Science Publications. ISBN 978-0-19-855370-0.
  27. ^ Peterson, W.; Holloway, H.; Coyle, A.; Williams, M. (septiembre de 1971). "Coordinación antiprismática sobre el xenón: la estructura del octafluoroxenato de nitrosonio (VI)". Science . 173 (4003): 1238–1239. Bibcode :1971Sci...173.1238P. doi :10.1126/science.173.4003.1238. ISSN  0036-8075. PMID  17775218. S2CID  22384146.
  28. ^ Hanson, Robert M. (1995). Origami molecular: modelos a escala de precisión a partir de papel . University Science Books. ISBN 978-0-935702-30-9.
  29. ^ ab Kaupp, Martin (2001). "Estructuras y enlaces "no VSEPR" en sistemas d0" (PDF) . Angew. Chem. Int. Ed. Engl. 40 (1): 3534–3565. doi :10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#. PMID  11592184.
  30. ^ Gillespie, Ronald J.; Noury, Stéphane; Pilmé, Julien; Silvi, Bernard (2004). "Estudio de la función de localización electrónica de la geometría de las moléculas d 0 de los metales del periodo 4 Ca a Mn". Inorg. Química. 43 (10): 3248–3256. doi :10.1021/ic0354015. PMID  15132634.
  31. ^ Landis, CR; Cleveland, T.; Firman, T.K. (1995). "Dando sentido a las formas de hidruros metálicos simples". J. Am. Chem. Soc. 117 (6): 1859–1860. doi :10.1021/ja00111a036.
  32. ^ Landis, CR; Cleveland, T.; Firman, T.K. (1996). "Estructura de W(CH3)6". Science . 272 ​​(5259): 179–183. doi : 10.1126/science.272.5259.179f .
  33. ^ Zhai, HJ; Li, S.; Dixon, DA; Wang, LS (2008). "Investigación de las propiedades electrónicas y estructurales de los cúmulos de óxido de cromo (CrO
    3    )−n
    ​    y (CrO 3 ) n ( n  = 1–5): espectroscopía de fotoelectrones y cálculos funcionales de densidad". Revista de la Sociedad Química Americana . 130 (15): 5167–77. doi :10.1021/ja077984d. PMID  18327905.
  34. ^ King, R. Bruce (2000). "Orbitales atómicos, simetría y poliedros de coordinación". Coord. Chem. Rev. 197 : 141–168. doi :10.1016/s0010-8545(99)00226-x.
  35. ^ Haalan, A.; Hammel, A.; Rydpal, K.; Volden, HV (1990). "La geometría de coordinación del hexametiltungsteno gaseoso no es octaédrica". J. Am. Chem. Soc. 112 (11): 4547–4549. doi :10.1021/ja00167a065.
  36. ^ Greenwood, Norman N. ; Earnshaw, Alan (1997). Química de los elementos (2.ª ed.). Butterworth-Heinemann . ISBN 978-0-08-037941-8.
  37. ^ Seijo, Luis; Barandiarán, Zoila; Huzinaga, Sigeru (1991). "Estudio del potencial del modelo ab initio de la geometría de equilibrio de dihaluros alcalinotérreos: MX2 (M = Mg, Ca, Sr, Ba; X = F, Cl, Br, I)" (PDF) . J. química. Física. 94 (5): 3762. Código bibliográfico : 1991JChPh..94.3762S. doi : 10.1063/1.459748. hdl : 10486/7315 .
  38. ^ Seth, Michael; Schwerdtfeger, Peter; Fægri, Knut (1999). "La química de los elementos superpesados. III. Estudios teóricos sobre los compuestos del elemento 113". Journal of Chemical Physics . 111 (14): 6422–6433. Bibcode :1999JChPh.111.6422S. doi : 10.1063/1.480168 . hdl : 2292/5178 . S2CID  41854842.
  39. ^ Bae, Ch.; Han, Y.-K.; Lee, Yo. S. (18 de enero de 2003). "Efectos de espín-órbita y relativistas en las estructuras y estabilidades de los fluoruros del grupo 17 EF 3 (E = I, At y elemento 117): estabilidad inducida por la relatividad para la estructura D 3h de (117)F 3 ". The Journal of Physical Chemistry A . 107 (6): 852–858. Bibcode :2003JPCA..107..852B. doi :10.1021/jp026531m.
  40. ^ Han, Young-Kyu; Lee, Yoon Sup (1999). "Estructuras de RgFn (Rg = Xe, Rn y elemento 118. n = 2, 4.) calculadas mediante métodos de espín-órbita de dos componentes. Un isómero inducido por espín-órbita de (118)F 4 ". Journal of Physical Chemistry A . 103 (8): 1104–1108. Bibcode :1999JPCA..103.1104H. doi :10.1021/jp983665k.
  41. ^ Anslyn, EV; Dougherty, DA (2006). Química orgánica física moderna . University Science Books. pág. 57. ISBN 978-1891389313.

Lectura adicional

  • Lagowski, JJ, ed. (2004). Química: fundamentos y aplicaciones . Vol. 3. Nueva York: Macmillan. Págs. 99-104. ISBN. 978-0-02-865721-9.
El Wikilibro A-level Chemistry/OCR (Salters) tiene una página sobre el tema: Geometría molecular y pares solitarios
  • VSEPR AR: visualización de la teoría VSEPR en 3D con aplicación de realidad aumentada
  • 3D Chem: química, estructuras y moléculas en 3D
  • Centro de Estructura Molecular de la Universidad de Indiana (IUMSC)
Obtenido de "https://es.wikipedia.org/w/index.php?title=Teoría_VSEPR&oldid=1256728170"