Icositetraedro pentagonal

Poliedro catalán

Icositetraedro pentagonal
(Haga clic en ccw* o cw para rotar modelos).*
Tipo	catalán
Notación de Conway	gC
Diagrama de Coxeter
Polígono de cara	pentágono irregular
Caras	24
Bordes	60
Vértices	38 = 6 + 8 + 24
Configuración de la cara	V3.3.3.3.4
Ángulo diedro	136° 18' 33'
Grupo de simetría	Oh , ⁠1/2⁠ ₃ antes de Cristo , [4,3] ⁺ , 432
Poliedro dual	cubo chato
Propiedades	convexo , transitivo de caras , quiral
Neto

Construcción geométrica de la constante de Tribonacci (AC), con compás y regla marcada, según el método descrito por Xerardo Neira.

En geometría , un icositetraedro pentagonal o icosikaitetraedro pentagonal ^[1] es un sólido catalán que es el dual del cubo romo . En cristalografía también se le llama giroide . ^[2]^[3]

Tiene dos formas distintas, que son imágenes especulares (o " enantiomorfos ") una de la otra.

Construcción

El icositetraedro pentagonal se puede construir a partir de un cubo romo sin tomar el dual. Se añaden pirámides cuadradas a las seis caras cuadradas del cubo romo, y pirámides triangulares a las ocho caras triangulares que no comparten una arista con un cuadrado. Las alturas de las pirámides se ajustan para que sean coplanares con las otras 24 caras triangulares del cubo romo. El resultado es el icositetraedro pentagonal.

Coordenadas cartesianas

Denotemos la constante de Tribonacci por . (Véase el cubo romo para una explicación geométrica de la constante de Tribonacci.) Las coordenadas cartesianas para los 38 vértices de un icositetraedro pentagonal centrado en el origen son las siguientes: $t\aprox. 1,839\,286\,755\,21$

las 12 permutaciones pares de $(\pm1, \pm(2 t +1), \pm t 2)$ con un número par de signos menos
las 12 permutaciones impares de $(\pm1, \pm(2 t +1), \pm t 2)$ con un número impar de signos menos
los 6 puntos $(\pm t 3, 0, 0)$ , $(0, \pm t 3, 0)$ y $(0, 0, \pm t 3)$
los 8 puntos $(\pm t 2, \pm t 2, \pm t 2)$

Las envolturas convexas para estos vértices ^[4] escaladas por dan como resultado un octaedro circunradio unitario centrado en el origen, un cubo unitario centrado en el origen escalado a y un cubo romo quiral irregular escalado a , como se visualiza en la siguiente figura: $estilo de visualización t^{-3}}$ $R\aproximadamente 0,9416969935$ ${\estilo de visualización R}$

Geometría

Las caras pentagonales tienen cuatro ángulos de y un ángulo de . El pentágono tiene tres aristas cortas de longitud unitaria cada una y dos aristas largas de longitud . El ángulo agudo está entre las dos aristas largas. El ángulo diedro es igual a . $\arccos((1-t)/2)\aproximadamente 114.812\,074\,477\,90^{\circ }$ $\arccos(2-t)\aproximadamente 80,751\,702\,088\,39^{\circ }$ $(t+1)/2\aproximadamente 1,419\,643\,377\,607\,08$ $\arccos(-1/(t^{2}-2))\aproximadamente 136,309\,232\,892\,32^{\circ }$

Si su cubo doble tiene una longitud de arista unitaria, su área de superficie y su volumen son: ^[5]

{\begin{aligned}A&=3{\sqrt {\frac {22(5t-1)}{4t-3}}}&&\aproximadamente 19,299\,94\\V&={\sqrt {\frac {11(t-4)}{2(20t-37)}}}&&\aproximadamente 7,4474\end{aligned}}

Proyecciones ortogonales

El icositetraedro pentagonal tiene tres posiciones de simetría, dos centradas en los vértices y una en el borde medio.

Proyecciones ortogonales
Simetría proyectiva	[3]	[4] ⁺	[2]
Imagen
Imagen dual

Variaciones

Se pueden construir variaciones isoédricas con la misma simetría octaédrica quiral con caras pentagonales que tienen 3 longitudes de arista.

Esta variación mostrada se puede construir agregando pirámides a 6 caras cuadradas y 8 caras triangulares de un cubo romo de modo que las nuevas caras triangulares con 3 triángulos coplanares se fusionen en caras pentagonales idénticas.

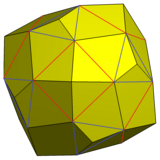Cubo de forma chata con pirámides aumentadas y caras fusionadas	Icositetraedro pentagonal	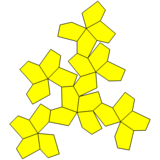Neto

Poliedros y teselaciones relacionados

Este poliedro está relacionado topológicamente como parte de una secuencia de poliedros y teselas de pentágonos con configuraciones de caras (V3.3.3.3. n ). (La secuencia progresa hacia teselas en el plano hiperbólico hasta cualquier n ). Estas figuras transitivas de caras tienen simetría rotacional (n32) .

n 32 mutaciones de simetría de teselaciones snub: 3.3.3.3.n en a mi
Simetría n.° 32	Esférico				Euclidiano	Hiperbólica compacta		Paracomp.
Simetría n.° 32	232	332	432	532	632	732	832	∞32
Figuras desairadas
Configuración.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Figuras de giroscopio
Configuración.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

El icositetraedro pentagonal es el segundo de una serie de poliedros y teselaciones duales con configuración de caras V3.3.4.3. n .

4 n 2 mutaciones de simetría de teselaciones snub: 3.3.4.3.n en a mi
Simetría 4 n 2	Esférico		Euclidiano	Hiperbólica compacta				Paracomp.
Simetría 4 n 2	242	342	442	542	642	742	842	∞42
Figuras desairadas
Configuración.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Figuras de giroscopio
Configuración.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

El icositetraedro pentagonal pertenece a una familia de duales de los poliedros uniformes relacionados con el cubo y el octaedro regular.

Poliedros octaédricos uniformes
Simetría : [4,3], (*432)							[4,3] ⁺ (432)	[1 ⁺ ,4,3] = [3,3] (*332)		[3 ⁺ ,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3 ^1,1 }	t{3,4} t{3 ^1,1 }	{3,4} {3 ^1,1 }	_{rr {}4,3} s2 {3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2 {4,3} t _{ 3,3}	s{3,4} s{3 ^1,1 }

		=	=	=				= o	= o	=

De poliedros duales a uniformes
V4 ³	Versión 3.8 ²	V(3.4) ²	Versión 4.6 ²	Versión 3 ⁴	Versión 3.4 ³	V4.6.8	V34.4	V3 ³	Versión 3.6 ²	V3 ⁵

Referencias

^ Conway, Simetrías de las cosas, p.284
^ "Promorfología de Cristales I".
^ "Forma, zonas y hábitos de los cristales". Archivado desde el original el 23 de agosto de 2003.
^ Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). "Sólidos Catalanes Derivados de Sistemas de Raíces 3D y Cuaterniones". Journal of Mathematical Physics . 51 (4). arXiv : 0908.3272 . doi :10.1063/1.3356985.
^ Weisstein, Eric W. , "Icositetraedro pentagonal" ("Sólido catalán") en MathWorld .

Williams, Robert (1979). La base geométrica de la estructura natural: un libro de consulta sobre diseño . Dover Publications, Inc. ISBN 0-486-23729-X.(Sección 3-9)
Wenninger, Magnus (1983), Modelos duales , Cambridge University Press , doi :10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, Sr. 0730208(Los trece poliedros convexos semirregulares y sus duales, página 28, Icositetraedro pentagonal)
Las simetrías de las cosas 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss , ISBN 978-1-56881-220-5 [1] (Capítulo 21, Denominación de los poliedros y teselaciones de Arquímedes y de Catalan, página 287, icosicaitetraedro pentagonal)

Enlaces externos

Icositetraedro pentagonal: modelo poliedro interactivo

[1] Conway, Simetrías de las cosas, p.284

[2] "Promorfología de Cristales I".

[3] "Forma, zonas y hábitos de los cristales". Archivado desde el original el 23 de agosto de 2003.

[4] Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). "Sólidos Catalanes Derivados de Sistemas de Raíces 3D y Cuaterniones". Journal of Mathematical Physics . 51 (4). arXiv : 0908.3272 . doi :10.1063/1.3356985.

[5] Weisstein, Eric W. , "Icositetraedro pentagonal" ("Sólido catalán") en MathWorld .