Antiprisma cuadrado chato
85.° equipo sólido de Johnson (26 caras)
Antiprisma cuadrado chato
TipoJohnson
J 84 – J 85 – J 86
Caras24 triángulos
2 cuadrados
Bordes40
Vértices16
Configuración de vértice 8 × 3 5 + 8 × 3 4 × 4 {\displaystyle 8\veces 3^{5}+8\veces 3^{4}\veces 4}
Grupo de simetría D 4 d Estilo de visualización D_{4d}}
Propiedadesconvexo
Neto
Modelo 3D de un antiprisma cuadrado romo

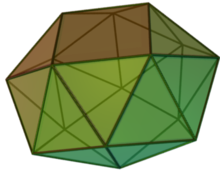
En geometría , el antiprisma cuadrado romo es el sólido de Johnson que se puede construir rozando el antiprisma cuadrado . Es uno de los sólidos de Johnson elementales que no surgen de manipulaciones de "cortar y pegar" de los sólidos platónicos y arquimedianos , aunque es un pariente del icosaedro que tiene simetría cuádruple en lugar de triple.

Construcción y propiedades

El antiprisma cuadrado romo es el proceso de construir poliedros cortando las caras de las aristas, girándolas y luego uniendo triángulos equiláteros a sus aristas. [1] Como sugiere el nombre, el antiprisma cuadrado romo se construye cortando el antiprisma cuadrado , [2] y esta construcción da como resultado 24 triángulos equiláteros y 2 cuadrados como sus caras. [3] Los sólidos de Johnson son los poliedros convexos cuyas caras son regulares, y el antiprisma cuadrado romo es uno de ellos, enumerado como , el 85.º sólido de Johnson. [4] Yo 85 Estilo de visualización J_ {85}}

Sea la raíz positiva del polinomio cúbico Además, sea definida por Entonces, las coordenadas cartesianas de un antiprisma cuadrado romo con longitud de arista 2 están dadas por la unión de las órbitas de los puntos bajo la acción del grupo generado por una rotación alrededor del eje - de 90° y por una rotación de 180° alrededor de una línea recta perpendicular al eje - y que forma un ángulo de 22,5° con el eje - . [5] Tiene la simetría tridimensional del grupo diedro de orden 16. [2] a ≈ 0,82354 {\displaystyle k\aproximadamente 0,82354} 9 incógnita 3 + 3 3 ( 5 − 2 ) incógnita 2 − 3 ( 5 − 2 2 ) incógnita − 17 3 + 7 6 . {\displaystyle 9x^{3}+3{\sqrt {3}}\left(5-{\sqrt {2}}\right)x^{2}-3\left(5-2{\sqrt {2}}\right)x-17{\sqrt {3}}+7{\sqrt {6}}.} yo ≈ 1.35374 {\displaystyle h\aprox 1,35374} yo = 2 + 8 + 2 3 a − 3 ( 2 + 2 ) a 2 4 3 − 3 a 2 . {\displaystyle h={\frac {{\sqrt {2}}+8+2{\sqrt {3}}k-3\left(2+{\sqrt {2}}\right)k^{2}}{4{\sqrt {3-3k^{2}}}}}.} ( 1 , 1 , yo ) , ( 1 + 3 a , 0 , yo − 3 − 3 a 2 ) {\displaystyle (1,1,h),\,\left(1+{\sqrt {3}}k,0,h-{\sqrt {3-3k^{2}}}\right)} el {\estilo de visualización z} el {\estilo de visualización z} incógnita {\estilo de visualización x} D 4 d Estilo de visualización D_{4d}}

El área de superficie y el volumen de un antiprisma cuadrado chato con longitud de arista se pueden calcular como: [3] a {\estilo de visualización a} A = ( 2 + 6 3 ) a 2 ≈ 12.392 a 2 , V ≈ 3.602 a 3 . {\displaystyle {\begin{aligned}A=\left(2+6{\sqrt {3}}\right)a^{2}&\approx 12.392a^{2},\\V&\approx 3.602a^{3}.\end{aligned}}}

Referencias

  1. ^ Holme, Audun (2010). Geometría: nuestro patrimonio cultural. Springer. pág. 99. doi :10.1007/978-3-642-14441-7. ISBN 978-3-642-14441-7.
  2. ^ ab Johnson, Norman W. (1966). "Poliedros convexos con caras regulares". Revista Canadiense de Matemáticas . 18 : 169–200. doi :10.4153/cjm-1966-021-8. MR  0185507. Zbl  0132.14603.
  3. ^ ab Berman, Martin (1971). "Poliedros convexos de caras regulares". Revista del Instituto Franklin . 291 (5): 329–352. doi :10.1016/0016-0032(71)90071-8. MR  0290245.
  4. ^ Francis, Darryl (2013). "Sólidos de Johnson y sus acrónimos". Word Ways . 46 (3): 177.
  5. ^ Timofeenko, AV (2009). "Los poliedros no compuestos no platónicos y no arquimedianos". Revista de Ciencias Matemáticas . 162 (5): 725. doi :10.1007/s10958-009-9655-0. S2CID  120114341.
Obtenido de "https://es.wikipedia.org/w/index.php?title=Antiprisma_cuadrado_redondeado&oldid=1234006160"