Antiprisma pentagonal
| Antiprisma pentagonal uniforme | |
|---|---|
 | |
| Tipo | Poliedro prismático uniforme |
| Elementos | F = 12, E = 20 V = 10 (χ = 2) |
| Caras por lados | 10{3}+2{5} |
| Símbolo de Schläfli | s{2,10} sr{2,5} |
| Símbolo de Wythoff | | 2 2 5 |
| Diagrama de Coxeter |      |
| Grupo de simetría | D 5d , [2 + ,10], (2*5), orden 20 |
| Grupo de rotación | D 5 , [5,2] + , (522), orden 10 |
| Referencias | U 77(c) |
| Dual | Trapezoedro pentagonal |
| Propiedades | convexo |
 Figura de vértice 3.3.3.5 | |
En geometría , el antiprisma pentagonal es el tercero de un conjunto infinito de antiprismas formados por una secuencia par de lados triangulares cerrados por dos casquetes poligonales. Está formado por dos pentágonos unidos entre sí por un anillo de diez triángulos para un total de doce caras. Por lo tanto, es un dodecaedro no regular .
Geometría
Si las caras del antiprisma pentagonal son todas regulares, se trata de un poliedro semirregular . También puede considerarse como un icosaedro parabidisminuido , una forma formada al eliminar dos pirámides pentagonales de un icosaedro regular, dejando dos caras pentagonales no adyacentes; una forma relacionada, el icosaedro metabidisminuido (uno de los sólidos de Johnson ), también se forma a partir del icosaedro al eliminar dos pirámides, pero sus caras pentagonales son adyacentes entre sí. Las dos caras pentagonales de cualquiera de las formas se pueden aumentar con pirámides para formar el icosaedro.
Relación con los politopos
El antiprisma pentagonal aparece como elemento constituyente en algunos politopos de dimensiones superiores . Dos anillos de diez antiprismas pentagonales cada uno delimitan la hipersuperficie del gran antiprisma de cuatro dimensiones . Si estos antiprismas se amplían con pirámides de prismas pentagonales y se unen con anillos de cinco tetraedros cada uno, se obtiene el conjunto de 600 celdas .
Véase también
El antiprisma pentagonal se puede truncar y alternar para formar un antiprisma chato :
| Antiprisma A5 | tA5 truncado | htA5 alternado |
|---|---|---|
|  |  |
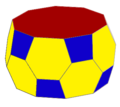| s{2,10} | ts{2,10} | ss{2,10} |
| v:10; e:20; f:12 | v:40; e:60; f:22 | v:20; e:50; f:32 |
| Nombre del antiprisma | Antiprisma digonal | Antiprisma triangular (trigonal) | Antiprisma cuadrado (tetragonal) | Antiprisma pentagonal | Antiprisma hexagonal | Antiprisma heptagonal | ... | Antiprisma apeirogonal |
|---|---|---|---|---|---|---|---|---|
| Imagen de poliedro |  |  |  | |  |  | ... | |
| Imagen de mosaico esférico |  |  |  |  |  |  | Imagen de mosaico plano |  |
| Configuración de vértice. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | ... | ∞.3.3.3 |
Antiprisma cruzado
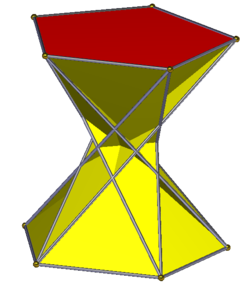
Un antiprisma pentagonal cruzado es topológicamente idéntico al antiprisma pentagonal , aunque no puede hacerse uniforme. Los lados son triángulos isósceles . Tiene simetría d 5d , orden 10. Su configuración de vértices es 3.3/2.3.5, con un triángulo retrógrado y su disposición de vértices es la misma que la de un prisma pentagonal .
Enlaces externos
- Weisstein, Eric W. "Antiprisma". MathWorld .
- [1]
- Antiprisma pentagonal: modelo poliedro interactivo
- Poliedros de realidad virtual www.georgehart.com: La enciclopedia de poliedros
- Modelo VRML
- poliedronismo A5
 | Este artículo relacionado con el poliedro es un esbozo . Puedes ayudar a Wikipedia expandiéndolo. |
