Dieléctrico

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «Dieléctrico» – noticias  · periódicos  · libros  · académico  · JSTOR ( diciembre de 2022 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Artículos sobre
Electromagnetismo
Electricidad Magnetismo Óptica Historia Computacional Libros de texto Fenómenos
Electrostática Densidad de carga Conductor Ley de Coulomb Electreto Carga eléctrica Dipolo eléctrico Campo eléctrico Flujo eléctrico Potencial eléctrico Descarga electrostática Inducción electrostática Ley de Gauss Aislante Permitividad Polarización Energía potencial Electricidad estática Triboelectricidad
Magnetostática Ley de Ampère Ley de Biot-Savart Ley magnética de Gauss Dipolo magnético Campo magnético Flujo magnético Potencial escalar magnético Potencial vectorial magnético Magnetización Permeabilidad Regla de la mano derecha
Electrodinámica Radiación de frenado Radiación ciclotrónica Corriente de desplazamiento Corriente de Foucault Campo electromagnético Inducción electromagnética Pulso electromagnético Radiación electromagnética Ley de Faraday Ecuaciones de Jefimenko Fórmula de Larmor Ley de Lenz Potencial de Liénard-Wiechert Ecuaciones de Londres Fuerza de Lorentz Ecuaciones de Maxwell Maxwell tensor Poynting vector Synchrotron radiation
Electrical network Alternating current Capacitance Current density Direct current Electric current Electric power Electrolysis Electromotive force Impedance Inductance Joule heating Kirchhoff laws Network analysis Ohm law Parallel circuit Resistance Resonant cavities Series circuit Voltage Watt Waveguides
Magnetic circuit AC motor DC motor Electric machine Electric motor Gyrator–capacitor Induction motor Linear motor Magnetomotive force Permeance Reluctance (complex) Reluctance (real) Rotor Stator Transformer
Covariant formulation Electromagnetic tensor Electromagnetism and special relativity Four-current Four-potential Mathematical descriptions Maxwell equations in curved spacetime Relativistic electromagnetism Stress–energy tensor
Scientists Ampère Biot Coulomb Davy Einstein Faraday Fizeau Gauss Heaviside Helmholtz Henry Hertz Hopkinson Jefimenko Joule Kelvin Kirchhoff Larmor Lenz Liénard Lorentz Maxwell Neumann Ohm Ørsted Poisson Poynting Ritchie Savart Singer Steinmetz Tesla Thomson Volta Weber Wiechert
v t e

En electromagnetismo , un dieléctrico (o medio dieléctrico ) es un aislante eléctrico que puede polarizarse mediante un campo eléctrico aplicado . Cuando un material dieléctrico se coloca en un campo eléctrico, las cargas eléctricas no fluyen a través del material como lo hacen en un conductor eléctrico , porque no tienen electrones sueltos o libres que puedan desplazarse a través del material, sino que se desplazan, solo ligeramente, de sus posiciones de equilibrio promedio, lo que provoca la polarización dieléctrica . Debido a la polarización dieléctrica , las cargas positivas se desplazan en la dirección del campo y las cargas negativas se desplazan en la dirección opuesta al campo. Esto crea un campo eléctrico interno que reduce el campo general dentro del propio dieléctrico. Si un dieléctrico está compuesto de moléculas débilmente enlazadas , esas moléculas no solo se polarizan, sino que también se reorientan de modo que sus ejes de simetría se alinean con el campo. ^[1]

El estudio de las propiedades dieléctricas se ocupa del almacenamiento y la disipación de energía eléctrica y magnética en los materiales. ^{[2] [3] [4]} Los dieléctricos son importantes para explicar diversos fenómenos en electrónica , óptica , física del estado sólido y biofísica celular . ^{[5] [6]}

Aunque el término aislante implica una baja conducción eléctrica , el término dieléctrico se refiere típicamente a materiales con una alta polarizabilidad . Esta última se expresa mediante un número llamado permitividad relativa . El término aislante se utiliza generalmente para indicar una obstrucción eléctrica, mientras que el término dieléctrico se utiliza para indicar la capacidad de almacenamiento de energía del material (por medio de la polarización). Un ejemplo común de un dieléctrico es el material eléctricamente aislante entre las placas metálicas de un condensador . La polarización del dieléctrico por el campo eléctrico aplicado aumenta la carga superficial del condensador para la intensidad del campo eléctrico dada. ^[1]

El término dieléctrico fue acuñado por William Whewell (de dia + eléctrico ) en respuesta a una solicitud de Michael Faraday . ^{[7] [8]}

Un dieléctrico perfecto es un material con conductividad eléctrica cero ( cf. conductor perfecto conductividad eléctrica infinita), ^[9] por lo que exhibe sólo una corriente de desplazamiento ; por lo tanto, almacena y devuelve energía eléctrica como si fuera un capacitor ideal.

La susceptibilidad eléctrica de un material dieléctrico es una medida de la facilidad con la que se polariza en respuesta a un campo eléctrico. Esto, a su vez, determina la permitividad eléctrica del material y, por lo tanto, influye en muchos otros fenómenos en ese medio, desde la capacitancia de los condensadores hasta la velocidad de la luz .${\displaystyle \chi _{e}}$

Se define como la constante de proporcionalidad (que puede ser un tensor ) que relaciona un campo eléctrico con la densidad de polarización dieléctrica inducida tal que${\displaystyle \mathbf {E} }$${\displaystyle \mathbf {P} }$

$${\displaystyle \mathbf {P} =\varepsilon _{0}\chi _{e}\mathbf {E} ,}$$

donde es la permitividad eléctrica del espacio libre .${\displaystyle \varepsilon _{0}}$

La susceptibilidad de un medio está relacionada con su permitividad relativa por${\displaystyle \varepsilon _{r}}$

$${\displaystyle \chi _{e}\ =\varepsilon _{r}-1.}$$

Así que en el caso de un vacío clásico ,

$${\displaystyle \chi _{e}\ =0.}$$

El desplazamiento eléctrico está relacionado con la densidad de polarización por${\displaystyle \mathbf {D} }$${\displaystyle \mathbf {P} }$

$${\displaystyle \mathbf {D} \ =\ \varepsilon _{0}\mathbf {E} +\mathbf {P} \ =\ \varepsilon _{0}\left(1+\chi _{e}\right)\mathbf {E} \ =\ \varepsilon _{0}\varepsilon _{r}\mathbf {E} .}$$

En general, un material no puede polarizarse instantáneamente en respuesta a un campo aplicado. La formulación más general en función del tiempo es

$${\displaystyle \mathbf {P} (t)=\varepsilon _{0}\int _{-\infty }^{t}\chi _{e}\left(t-t'\right)\mathbf {E} (t')\,dt'.}$$

Es decir, la polarización es una convolución del campo eléctrico en tiempos anteriores con susceptibilidad dependiente del tiempo dada por . El límite superior de esta integral puede extenderse hasta el infinito también si se define para . Una respuesta instantánea corresponde a la susceptibilidad de la función delta de Dirac .${\displaystyle \chi _{e}(\Delta t)}$${\displaystyle \chi _{e}(\Delta t)=0}$${\displaystyle \Delta t<0}$${\displaystyle \chi _{e}(\Delta t)=\chi _{e}\delta (\Delta t)}$

En un sistema lineal es más conveniente tomar la transformada de Fourier y escribir esta relación como una función de la frecuencia. Debido al teorema de convolución , la integral se convierte en un producto simple,$${\displaystyle \mathbf {P} (\omega )=\varepsilon _{0}\chi _{e}(\omega )\mathbf {E} (\omega ).}$$

La susceptibilidad (o equivalentemente, la permitividad) depende de la frecuencia. El cambio de susceptibilidad con respecto a la frecuencia caracteriza las propiedades de dispersión del material.

Además, el hecho de que la polarización sólo puede depender del campo eléctrico en tiempos anteriores (es decir, para ), una consecuencia de la causalidad , impone restricciones de Kramers-Kronig sobre las partes reales e imaginarias de la susceptibilidad .${\displaystyle \chi _{e}(\Delta t)=0}$${\displaystyle \Delta t<0}$${\displaystyle \chi _{e}(\omega )}$

En el enfoque clásico del dieléctrico, el material está formado por átomos. Cada átomo está formado por una nube de carga negativa (electrones) unida a una carga puntual positiva en su centro y que la rodea. En presencia de un campo eléctrico, la nube de carga se distorsiona, como se muestra en la parte superior derecha de la figura.

Esto se puede reducir a un simple dipolo utilizando el principio de superposición . Un dipolo se caracteriza por su momento dipolar , una cantidad vectorial que se muestra en la figura como la flecha azul etiquetada como M. Es la relación entre el campo eléctrico y el momento dipolar lo que da lugar al comportamiento del dieléctrico. (Tenga en cuenta que el momento dipolar apunta en la misma dirección que el campo eléctrico en la figura. Esto no siempre es así y es una simplificación importante, pero es cierto para muchos materiales).

Cuando se elimina el campo eléctrico, el átomo vuelve a su estado original. El tiempo necesario para ello se denomina tiempo de relajación ; una desintegración exponencial.

Ésta es la esencia del modelo en física. El comportamiento del dieléctrico depende ahora de la situación. Cuanto más complicada sea la situación, más rico debe ser el modelo para describir con precisión el comportamiento. Las preguntas importantes son:

• ¿El campo eléctrico es constante o varía con el tiempo? ¿A qué ritmo?
• ¿La respuesta depende de la dirección del campo aplicado ( isotropía del material)?
• ¿La respuesta es la misma en todas partes ( homogeneidad del material)?
• ¿Hay que tener en cuenta algún límite o interfaz?
• ¿La respuesta es lineal con respecto al campo o existen no linealidades ?

La relación entre el campo eléctrico E y el momento dipolar M da lugar al comportamiento del dieléctrico, que, para un material dado, puede caracterizarse por la función F definida por la ecuación:$${\displaystyle \mathbf {M} =\mathbf {F} (\mathbf {E} ).}$$

Una vez definidos tanto el tipo de campo eléctrico como el tipo de material, se elige la función F más simple que prediga correctamente los fenómenos de interés. Algunos ejemplos de fenómenos que pueden modelarse de esta manera son:

• Índice de refracción
• Dispersión de velocidad de grupo
• Birrefringencia
• Enfoque en uno mismo
• Generación de armónicos

La polarización dipolar es una polarización que es inherente a las moléculas polares (polarización de orientación) o puede ser inducida en cualquier molécula en la que sea posible la distorsión asimétrica de los núcleos (polarización de distorsión). La polarización de orientación resulta de un dipolo permanente, por ejemplo, que surge del ángulo de 104,45° entre los enlaces asimétricos entre los átomos de oxígeno e hidrógeno en la molécula de agua, que conserva la polarización en ausencia de un campo eléctrico externo. El conjunto de estos dipolos forma una polarización macroscópica.

Cuando se aplica un campo eléctrico externo, la distancia entre cargas dentro de cada dipolo permanente, que está relacionada con el enlace químico , permanece constante en la polarización de orientación; sin embargo, la dirección de polarización en sí misma gira. Esta rotación ocurre en una escala de tiempo que depende del torque y la viscosidad local circundante de las moléculas. Debido a que la rotación no es instantánea, las polarizaciones dipolares pierden la respuesta a los campos eléctricos en las frecuencias más altas. Una molécula gira alrededor de 1 radián por picosegundo en un fluido, por lo tanto, esta pérdida ocurre a aproximadamente 10 ¹¹ Hz (en la región de microondas). El retraso de la respuesta al cambio del campo eléctrico causa fricción y calor.

Cuando se aplica un campo eléctrico externo a frecuencias infrarrojas o inferiores, las moléculas se doblan y estiran por el campo y el momento dipolar molecular cambia. La frecuencia de vibración molecular es aproximadamente la inversa del tiempo que tardan las moléculas en doblarse, y esta polarización distorsionada desaparece por encima del infrarrojo.

La polarización iónica es la polarización causada por desplazamientos relativos entre iones positivos y negativos en cristales iónicos (por ejemplo, NaCl ).

Si un cristal o molécula está formado por átomos de más de un tipo, la distribución de cargas alrededor de un átomo en el cristal o molécula tiende a ser positiva o negativa. Como resultado, cuando las vibraciones reticulares o las vibraciones moleculares inducen desplazamientos relativos de los átomos, los centros de cargas positivas y negativas también se desplazan. La ubicación de estos centros se ve afectada por la simetría de los desplazamientos. Cuando los centros no se corresponden, surge la polarización en las moléculas o cristales. Esta polarización se denomina polarización iónica .

La polarización iónica provoca el efecto ferroeléctrico , así como la polarización dipolar. La transición ferroeléctrica, que se produce por la alineación de las orientaciones de los dipolos permanentes a lo largo de una dirección determinada, se denomina transición de fase de orden-desorden . La transición causada por polarizaciones iónicas en los cristales se denomina transición de fase desplazativa .

La polarización iónica permite la producción de compuestos ricos en energía en las células (la bomba de protones en las mitocondrias ) y, en la membrana plasmática , el establecimiento del potencial de reposo , el transporte energéticamente desfavorable de iones y la comunicación de célula a célula (la Na+/K+-ATPasa ).

Todas las células de los tejidos corporales animales están polarizadas eléctricamente; en otras palabras, mantienen una diferencia de voltaje a través de la membrana plasmática de la célula , conocida como potencial de membrana . Esta polarización eléctrica es el resultado de una interacción compleja entre los transportadores de iones y los canales de iones .

En las neuronas, los tipos de canales iónicos en la membrana suelen variar en las distintas partes de la célula, lo que confiere a las dendritas , al axón y al cuerpo celular propiedades eléctricas diferentes. Como resultado, algunas partes de la membrana de una neurona pueden ser excitables (capaces de generar potenciales de acción), mientras que otras no.

En física, la dispersión dieléctrica es la dependencia de la permitividad de un material dieléctrico con respecto a la frecuencia de un campo eléctrico aplicado. Debido a que existe un desfase entre los cambios en la polarización y los cambios en el campo eléctrico, la permitividad del dieléctrico es una función compleja de la frecuencia del campo eléctrico. La dispersión dieléctrica es muy importante para las aplicaciones de materiales dieléctricos y el análisis de sistemas de polarización.

Este es un ejemplo de un fenómeno general conocido como dispersión material : una respuesta dependiente de la frecuencia de un medio para la propagación de ondas.

Cuando la frecuencia se hace más alta:

1. La polarización dipolar ya no puede seguir las oscilaciones del campo eléctrico en la región de microondas alrededor de 10 ¹⁰ Hz .
2. La polarización iónica y la polarización por distorsión molecular ya no pueden rastrear el campo eléctrico más allá de la región infrarroja o infrarroja lejana alrededor de 10 ¹³ Hz,
3. La polarización electrónica pierde su respuesta en la región ultravioleta alrededor de 10 ¹⁵ Hz.

En la región de frecuencias por encima del ultravioleta, la permitividad se acerca a la constante ε ₀ en cada sustancia, donde ε ₀ es la permitividad del espacio libre. Debido a que la permitividad indica la fuerza de la relación entre un campo eléctrico y la polarización, si un proceso de polarización pierde su respuesta, la permitividad disminuye.

La relajación dieléctrica es el retraso momentáneo (o desfase) en la constante dieléctrica de un material. Esto suele deberse al retraso en la polarización molecular con respecto a un campo eléctrico cambiante en un medio dieléctrico (por ejemplo, en el interior de condensadores o entre dos grandes superficies conductoras ). La relajación dieléctrica en campos eléctricos cambiantes podría considerarse análoga a la histéresis en campos magnéticos cambiantes (por ejemplo, en núcleos de inductores o transformadores ). La relajación en general es un retraso o desfase en la respuesta de un sistema lineal y, por lo tanto, la relajación dieléctrica se mide en relación con los valores dieléctricos lineales de estado estable (equilibrio) esperados. El desfase temporal entre el campo eléctrico y la polarización implica una degradación irreversible de la energía libre de Gibbs .

En física , la relajación dieléctrica se refiere a la respuesta de relajación de un medio dieléctrico a un campo eléctrico externo oscilante. Esta relajación se describe a menudo en términos de permitividad en función de la frecuencia , que, para sistemas ideales, puede describirse mediante la ecuación de Debye. Por otro lado, la distorsión relacionada con la polarización iónica y electrónica muestra un comportamiento de tipo resonancia u oscilador . El carácter del proceso de distorsión depende de la estructura, la composición y el entorno de la muestra.

La relajación de Debye es la respuesta de relajación dieléctrica de una población ideal de dipolos que no interactúan con un campo eléctrico externo alterno. Generalmente se expresa en la permitividad compleja ε de un medio en función de la frecuencia angular del campo ω :

$${\displaystyle {\hat {\varepsilon }}(\omega )=\varepsilon _{\infty }+{\frac {\Delta \varepsilon }{1+i\omega \tau }},}$$

donde ε _∞ es la permitividad en el límite de alta frecuencia, Δ ε = ε _s − ε _∞ donde ε _s es la permitividad estática de baja frecuencia y τ es el tiempo de relajación característico del medio. Al separar la permitividad dieléctrica compleja en la parte real y la parte imaginaria, se obtiene: ^[10]${\displaystyle \varepsilon '}$${\displaystyle \varepsilon ''}$

$${\displaystyle {\begin{aligned}\varepsilon '&=\varepsilon _{\infty }+{\frac {\varepsilon _{s}-\varepsilon _{\infty }}{1+\omega ^{2}\tau ^{2}}}\\[3pt]\varepsilon ''&={\frac {(\varepsilon _{s}-\varepsilon _{\infty })\omega \tau }{1+\omega ^{2}\tau ^{2}}}\end{aligned}}}$$

Nótese que la ecuación anterior para a veces se escribe con en el denominador debido a una ambigüedad en la convención de signos por la cual muchas fuentes representan la dependencia temporal del campo eléctrico complejo con mientras que otras usan . En la primera convención, las funciones y que representan partes reales e imaginarias se dan por mientras que en la segunda convención . La ecuación anterior usa la última convención. ^[11]${\displaystyle {\hat {\varepsilon }}(\omega )}$${\displaystyle 1-i\omega \tau }$${\displaystyle \exp(-i\omega t)}$${\displaystyle \exp(+i\omega t)}$${\displaystyle \varepsilon '}$${\displaystyle \varepsilon ''}$${\displaystyle {\hat {\varepsilon }}(\omega )=\varepsilon '+i\varepsilon ''}$${\displaystyle {\hat {\varepsilon }}(\omega )=\varepsilon '-i\varepsilon ''}$

La pérdida dieléctrica también está representada por la tangente de pérdida:

$${\displaystyle \tan(\delta )={\frac {\varepsilon ''}{\varepsilon '}}={\frac {\left(\varepsilon _{s}-\varepsilon _{\infty }\right)\omega \tau }{\varepsilon _{s}+\varepsilon _{\infty }\omega ^{2}\tau ^{2}}}}$$

Este modelo de relajación fue introducido por el físico Peter Debye (1913) y recibió su nombre en honor a él. ^[12] Es característico de la polarización dinámica con un solo tiempo de relajación.

Ecuación de Cole-Cole

Esta ecuación se utiliza cuando el pico de pérdida dieléctrica muestra un ensanchamiento simétrico.

Ecuación de Cole-Davidson

Esta ecuación se utiliza cuando el pico de pérdida dieléctrica muestra un ensanchamiento asimétrico.

Relajación Havriliak-Negami

Esta ecuación considera tanto el ensanchamiento simétrico como el asimétrico.

Función de Kohlrausch-Williams-Watts

Transformada de Fourier de una función exponencial estirada .

Ley de Curie-von Schweidler

Esto muestra la respuesta de los dieléctricos a un campo de CC aplicado para comportarse de acuerdo con una ley de potencia, que puede expresarse como una integral sobre funciones exponenciales ponderadas.

Aproximación de Djordjevic-Sarkar

Esto se utiliza cuando la pérdida dieléctrica es aproximadamente constante para un amplio rango de frecuencias.

La paraelectricidad es el comportamiento nominal de los dieléctricos cuando el tensor de permitividad dieléctrica es proporcional a la matriz unitaria, es decir, un campo eléctrico aplicado provoca polarización y/o alineación de dipolos solo en paralelo al campo eléctrico aplicado. Contrariamente a la analogía con un material paramagnético, no es necesario que exista un dipolo eléctrico permanente en un material paraeléctrico. La eliminación de los campos da como resultado que la polarización dipolar vuelva a cero. ^[13] Los mecanismos que causan el comportamiento paraeléctrico son la distorsión de iones individuales (desplazamiento de la nube de electrones desde el núcleo) y la polarización de moléculas o combinaciones de iones o defectos.

La paraelectricidad puede ocurrir en fases cristalinas donde los dipolos eléctricos no están alineados y, por lo tanto, tienen el potencial de alinearse en un campo eléctrico externo y debilitarlo.

La mayoría de los materiales dieléctricos son paraeléctricos. Un ejemplo específico de un material paraeléctrico de constante dieléctrica alta es el titanato de estroncio .

El cristal de LiNbO ₃ es ferroeléctrico por debajo de 1430 K y, por encima de esta temperatura, se transforma en una fase paraeléctrica desordenada. De manera similar, otras perovskitas también presentan paraelectricidad a altas temperaturas.

Se ha explorado la paraelectricidad como un posible mecanismo de refrigeración; polarizar un paraeléctrico mediante la aplicación de un campo eléctrico en condiciones de proceso adiabático aumenta la temperatura, mientras que eliminar el campo la reduce. ^[14] Una bomba de calor que funciona polarizando el paraeléctrico, lo que le permite volver a la temperatura ambiente (al disipar el calor adicional), poniéndolo en contacto con el objeto a enfriar y finalmente despolarizándolo, daría como resultado la refrigeración.

Los dieléctricos sintonizables son aislantes cuya capacidad para almacenar carga eléctrica cambia cuando se aplica un voltaje. ^[15]

Generalmente, el titanato de estroncio ( SrTiO
₃) se utiliza para dispositivos que funcionan a bajas temperaturas, mientras que el titanato de bario y estroncio ( Ba
_1−xSr
_incógnitaTiO
₃) sustitutos de los dispositivos a temperatura ambiente. Otros materiales potenciales incluyen dieléctricos de microondas y compuestos de nanotubos de carbono (CNT). ^{[15] [16] [17]}

En 2013, capas de múltiples láminas de titanato de estroncio intercaladas con capas individuales de óxido de estroncio produjeron un dieléctrico capaz de operar a hasta 125 GHz. El material se creó mediante epitaxia de haz molecular . Los dos tienen un espaciado desigual de los cristales que produce tensión dentro de la capa de titanato de estroncio que la hace menos estable y ajustable. ^[15]

Sistemas como Ba
_1−xSr
_incógnitaTiO
₃Tienen una transición paraeléctrica-ferroeléctrica justo por debajo de la temperatura ambiente, lo que proporciona una alta capacidad de ajuste. Las películas sufren pérdidas significativas que surgen de los defectos.

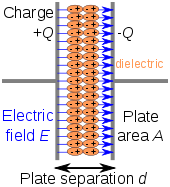
Los condensadores fabricados comercialmente suelen utilizar un material dieléctrico sólido con alta permitividad como medio intermedio entre las cargas positivas y negativas almacenadas. Este material suele denominarse en contextos técnicos dieléctrico del condensador . ^[18]

La ventaja más obvia de utilizar un material dieléctrico de este tipo es que evita que las placas conductoras, en las que se almacenan las cargas, entren en contacto eléctrico directo. Sin embargo, lo más importante es que una permitividad alta permite almacenar una mayor carga a un voltaje dado. Esto se puede ver al tratar el caso de un dieléctrico lineal con permitividad ε y espesor d entre dos placas conductoras con densidad de carga uniforme σ _ε . En este caso, la densidad de carga viene dada por

$${\displaystyle \sigma _{\varepsilon }=\varepsilon {\frac {V}{d}}}$$

y la capacitancia por unidad de área por

$${\displaystyle c={\frac {\sigma _{\varepsilon }}{V}}={\frac {\varepsilon }{d}}}$$

A partir de esto, se puede ver fácilmente que un ε mayor conduce a una mayor carga almacenada y, por lo tanto, a una mayor capacitancia.

Los materiales dieléctricos utilizados para los condensadores también se eligen de manera que sean resistentes a la ionización . Esto permite que el condensador funcione a voltajes más altos antes de que el dieléctrico aislante se ionice y comience a permitir el paso de corrientes no deseadas.

Un oscilador resonador dieléctrico (DRO) es un componente electrónico que muestra resonancia de la respuesta de polarización para un rango estrecho de frecuencias, generalmente en la banda de microondas. Consiste en un "disco" de cerámica que tiene una constante dieléctrica grande y un factor de disipación bajo . Dichos resonadores se utilizan a menudo para proporcionar una referencia de frecuencia en un circuito oscilador. Un resonador dieléctrico sin blindaje se puede utilizar como una antena resonadora dieléctrica (DRA).

Entre 2002 y 2004, el Laboratorio de Investigación del Ejército de los Estados Unidos (ARL) llevó a cabo investigaciones sobre tecnología de película delgada. Se estudió el titanato de bario y estroncio (BST), una película delgada ferroeléctrica, para la fabricación de componentes de radiofrecuencia y microondas, como osciladores controlados por voltaje, filtros sintonizables y desfasadores. ^[19]

La investigación fue parte de un esfuerzo para proporcionar al Ejército materiales altamente ajustables y compatibles con microondas para dispositivos ajustables por campo eléctrico de banda ancha, que operan de manera consistente en temperaturas extremas. ^[20] Este trabajo mejoró la capacidad de ajuste del titanato de bario y estroncio a granel, que es un facilitador de película delgada para componentes electrónicos. ^[21]

En un artículo de investigación de 2004, los investigadores del ARL de EE. UU. exploraron cómo pequeñas concentraciones de dopantes aceptores pueden modificar drásticamente las propiedades de materiales ferroeléctricos como el BST. ^[22]

Los investigadores "doparon" películas delgadas de BST con magnesio y analizaron la "estructura, la microestructura, la morfología de la superficie y la calidad de la composición de la película/sustrato" del resultado. Las películas de BST dopadas con Mg mostraron "propiedades dieléctricas mejoradas, baja corriente de fuga y buena capacidad de ajuste", lo que las hace potencialmente aptas para su uso en dispositivos sintonizables por microondas. ^[19]

Los materiales dieléctricos pueden ser sólidos, líquidos o gases. (El alto vacío también puede ser un dieléctrico útil, ^[23] casi sin pérdidas, aunque su constante dieléctrica relativa sea solo la unidad).

Los dieléctricos sólidos son quizás los más utilizados en ingeniería eléctrica, y muchos sólidos son muy buenos aislantes. Algunos ejemplos son la porcelana , el vidrio y la mayoría de los plásticos . El aire, el nitrógeno y el hexafluoruro de azufre son los tres dieléctricos gaseosos más utilizados .

• Los recubrimientos industriales como el parileno proporcionan una barrera dieléctrica entre el sustrato y su entorno.
• El aceite mineral se utiliza ampliamente en el interior de los transformadores eléctricos como fluido dieléctrico y para ayudar a la refrigeración. Los fluidos dieléctricos con constantes dieléctricas más altas, como el aceite de ricino de grado eléctrico , se utilizan a menudo en los condensadores de alta tensión para ayudar a prevenir la descarga de corona y aumentar la capacitancia.
• Debido a que los dieléctricos resisten el flujo de electricidad, la superficie de un dieléctrico puede retener cargas eléctricas sobrantes. Esto puede ocurrir accidentalmente cuando se frota el dieléctrico ( efecto triboeléctrico ). Esto puede ser útil, como en un generador de Van de Graaff o un electróforo , o puede ser potencialmente destructivo, como en el caso de una descarga electrostática .
• Los dieléctricos especialmente procesados, llamados electretos (que no deben confundirse con los ferroeléctricos ), pueden retener un exceso de carga interna o una polarización "congelada". Los electretos tienen un campo eléctrico semipermanente y son el equivalente electrostático de los imanes. Los electretos tienen numerosas aplicaciones prácticas en el hogar y la industria.
• Algunos dieléctricos pueden generar una diferencia de potencial cuando se someten a una tensión mecánica o (de manera equivalente) cambiar de forma física si se aplica un voltaje externo a través del material. Esta propiedad se denomina piezoelectricidad . Los materiales piezoeléctricos son otra clase de dieléctricos muy útiles.
• Algunos cristales iónicos y dieléctricos poliméricos presentan un momento dipolar espontáneo, que puede revertirse mediante un campo eléctrico aplicado externamente. Este comportamiento se denomina efecto ferroeléctrico . Estos materiales son análogos a la forma en que se comportan los materiales ferromagnéticos dentro de un campo magnético aplicado externamente. Los materiales ferroeléctricos suelen tener constantes dieléctricas muy altas, lo que los hace muy útiles para los condensadores.

• Jackson, John David (10 de agosto de 1998) [1962]. Electrodinámica clásica (3.ª ed.). John Wiley & Sons . ISBN 978-0-471-30932-1.OCLC 535998  .
• Scaife, Brendan KP (3 de septiembre de 1998). Principios de dieléctricos. Monografías sobre física y química de materiales (2.ª ed.). Oxford University Press . ISBN 978-0-198-56557-4.

• Conferencia de Feynman sobre dieléctricos
• Esfera dieléctrica en un campo eléctrico
• Paquete de enseñanza y aprendizaje de Difusión de TI para la promoción de la ciencia de los materiales (DoITPoMS) "Materiales dieléctricos" de la Universidad de Cambridge
• Textos en Wikisource:
  • "Dieléctrico". Enciclopedia Americana . 1920.
  • "Dieléctrico". Enciclopedia Británica (11ª ed.). 1911.