Circunvolución

En matemáticas (en particular, análisis funcional ), la convolución es una operación matemática sobre dos funciones ( y ) que produce una tercera función ( ). El término convolución se refiere tanto a la función resultante como al proceso de calcularla. Se define como la integral del producto de las dos funciones después de que una se refleja sobre el eje y y se desplaza. La integral se evalúa para todos los valores de desplazamiento, produciendo la función de convolución. La elección de qué función se refleja y se desplaza antes de la integral no cambia el resultado integral (ver conmutatividad). Gráficamente, expresa cómo la "forma" de una función es modificada por la otra.${\estilo de visualización f}$${\estilo de visualización g}$${\estilo de visualización f*g}$

Algunas características de la convolución son similares a la correlación cruzada : para funciones de valores reales, de una variable continua o discreta, la convolución ( )${\estilo de visualización f*g}$ difiere de la correlación cruzada ( ) solo en que o se refleja sobre el eje y en la convolución; por lo tanto, es una correlación cruzada de y , o y . ^[A]  Para funciones de valores complejos, el operador de correlación cruzada es el adjunto del operador de convolución.${\displaystyle f\star g}$${\estilo de visualización f(x)}$${\estilo de visualización g(x)}$${\displaystyle g(-x)}$${\estilo de visualización f(x)}$${\estilo de visualización f(-x)}$${\estilo de visualización g(x)}$

La convolución tiene aplicaciones que incluyen probabilidad , estadística , acústica , espectroscopia , procesamiento de señales y procesamiento de imágenes , geofísica , ingeniería , física , visión artificial y ecuaciones diferenciales . ^[1]

La convolución puede definirse para funciones en el espacio euclidiano y otros grupos (como estructuras algebraicas ). ^{[ cita requerida ]} Por ejemplo, las funciones periódicas , como la transformada de Fourier de tiempo discreto , pueden definirse en un círculo y convolucionarse mediante convolución periódica . (Véase la fila 18 en DTFT § Propiedades ). Una convolución discreta puede definirse para funciones en el conjunto de números enteros .

Las generalizaciones de convolución tienen aplicaciones en el campo del análisis numérico y el álgebra lineal numérica , y en el diseño e implementación de filtros de respuesta de impulso finito en el procesamiento de señales. ^{[ cita requerida ]}

El cálculo de la inversa de la operación de convolución se conoce como deconvolución .

La convolución de y se escribe , denotando al operador con el símbolo . ^[B] Se define como la integral del producto de las dos funciones después de que una se refleja sobre el eje y y se desplaza. Como tal, es un tipo particular de transformación integral :${\estilo de visualización f}$${\estilo de visualización g}$${\estilo de visualización f*g}$${\estilo de visualización *}$

${\displaystyle (f*g)(t):=\int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau .}$

Una definición equivalente es (ver conmutatividad):

${\displaystyle (f*g)(t):=\int _{-\infty }^{\infty }f(t-\tau )g(\tau )\,d\tau .}$

Si bien el símbolo se utiliza arriba, no necesita representar el dominio del tiempo. En cada , la fórmula de convolución se puede describir como el área bajo la función ponderada por la función desplazada por la cantidad . A medida que cambia, la función de ponderación enfatiza diferentes partes de la función de entrada ; Si es un valor positivo, entonces es igual a que se desliza o se desplaza a lo largo del eje hacia la derecha (hacia ) por la cantidad de , mientras que si es un valor negativo, entonces es igual a que se desliza o se desplaza hacia la izquierda (hacia ) por la cantidad de .${\displaystyle t}$${\displaystyle t}$${\displaystyle f(\tau )}$${\displaystyle g(-\tau )}$${\displaystyle t}$${\displaystyle t}$${\displaystyle g(t-\tau )}$${\displaystyle f(\tau )}$${\displaystyle t}$${\displaystyle g(t-\tau )}$${\displaystyle g(-\tau )}$${\displaystyle \tau }$${\displaystyle +\infty }$${\displaystyle t}$${\displaystyle t}$${\displaystyle g(t-\tau )}$${\displaystyle g(-\tau )}$${\displaystyle -\infty }$${\displaystyle |t|}$

Para las funciones admitidas únicamente en (es decir, cero para argumentos negativos), los límites de integración se pueden truncar, lo que da como resultado:${\displaystyle f}$${\displaystyle g}$ ${\displaystyle [0,\infty )}$

${\displaystyle (f*g)(t)=\int _{0}^{t}f(\tau )g(t-\tau )\,d\tau \quad \ {\text{for }}f,g:[0,\infty )\to \mathbb {R} .}$

Para la formulación multidimensional de la convolución, consulte el dominio de definición (a continuación).

Una convención de notación de ingeniería común es: ^[2]

${\displaystyle f(t)*g(t)\mathrel {:=} \underbrace {\int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau } _{(f*g)(t)},}$

que debe interpretarse con cuidado para evitar confusiones. Por ejemplo, es equivalente a , pero en realidad es equivalente a . ^[3]${\displaystyle f(t)*g(t-t_{0})}$${\displaystyle (f*g)(t-t_{0})}$${\displaystyle f(t-t_{0})*g(t-t_{0})}$${\displaystyle (f*g)(t-2t_{0})}$

Dadas dos funciones y con transformadas de Laplace bilaterales (transformada de Laplace de dos lados)${\displaystyle f(t)}$${\displaystyle g(t)}$

${\displaystyle F(s)=\int _{-\infty }^{\infty }e^{-su}\ f(u)\ {\text{d}}u}$

y

${\displaystyle G(s)=\int _{-\infty }^{\infty }e^{-sv}\ g(v)\ {\text{d}}v}$

respectivamente, la operación de convolución se puede definir como la transformada de Laplace inversa del producto de y . ^{[4] [5]} Más precisamente,${\displaystyle (f*g)(t)}$${\displaystyle F(s)}$${\displaystyle G(s)}$

${\displaystyle {\begin{aligned}F(s)\cdot G(s)&=\int _{-\infty }^{\infty }e^{-su}\ f(u)\ {\text{d}}u\cdot \int _{-\infty }^{\infty }e^{-sv}\ g(v)\ {\text{d}}v\\&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-s(u+v)}\ f(u)\ g(v)\ {\text{d}}u\ {\text{d}}v\end{aligned}}}$

Sea tal que${\displaystyle t=u+v}$

${\displaystyle {\begin{aligned}F(s)\cdot G(s)&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }e^{-st}\ f(u)\ g(t-u)\ {\text{d}}u\ {\text{d}}t\\&=\int _{-\infty }^{\infty }e^{-st}\underbrace {\int _{-\infty }^{\infty }f(u)\ g(t-u)\ {\text{d}}u} _{(f*g)(t)}\ {\text{d}}t\\&=\int _{-\infty }^{\infty }e^{-st}(f*g)(t)\ {\text{d}}t\end{aligned}}}$

Nótese que es la transformada de Laplace bilateral de . Se puede hacer una derivación similar utilizando la transformada de Laplace unilateral (transformada de Laplace unilateral).${\displaystyle F(s)\cdot G(s)}$${\displaystyle (f*g)(t)}$

La operación de convolución también describe la salida (en términos de la entrada) de una clase importante de operaciones conocidas como operaciones lineales invariantes en el tiempo (LTI). Véase la teoría de sistemas LTI para una derivación de la convolución como resultado de las restricciones LTI. En términos de las transformadas de Fourier de la entrada y la salida de una operación LTI, no se crean nuevos componentes de frecuencia. Los existentes solo se modifican (amplitud y/o fase). En otras palabras, la transformada de salida es el producto puntual de la transformada de entrada con una tercera transformada (conocida como función de transferencia ). Véase el teorema de convolución para una derivación de esa propiedad de la convolución. A la inversa, la convolución puede derivarse como la transformada de Fourier inversa del producto puntual de dos transformadas de Fourier.

Expresar cada función en términos de una variable ficticia ${\displaystyle \tau .}$ Refleja una de las funciones: →${\displaystyle g(\tau )}$${\displaystyle g(-\tau ).}$ Añade un desfase temporal que permite deslizarse a lo largo del eje . Si t es un valor positivo, entonces es igual a que se desliza o se desplaza a lo largo del eje hacia la derecha (hacia ) en la cantidad de . Si es un valor negativo, entonces es igual a que se desliza o se desplaza hacia la izquierda (hacia ) en la cantidad de .${\displaystyle t}$${\displaystyle g(-\tau )}$${\displaystyle \tau }$${\displaystyle g(t-\tau )}$${\displaystyle g(-\tau )}$${\displaystyle \tau }$${\displaystyle +\infty }$${\displaystyle t}$${\displaystyle t}$${\displaystyle g(t-\tau )}$${\displaystyle g(-\tau )}$${\displaystyle -\infty }$${\displaystyle |t|}$ Comience en y deslícelo hasta el final . En cualquier punto en que se intersequen las dos funciones, encuentre la integral de su producto. En otras palabras, en el momento , calcule el área bajo la función ponderada por la función de ponderación.${\displaystyle t}$${\displaystyle -\infty }$${\displaystyle +\infty }$${\displaystyle t}$${\displaystyle f(\tau )}$${\displaystyle g(t-\tau ).}$ La forma de onda resultante (no se muestra aquí) es la convolución de las funciones y .${\displaystyle f}$${\displaystyle g}$ Si es un impulso unitario , el resultado de este proceso es simplemente . Formalmente: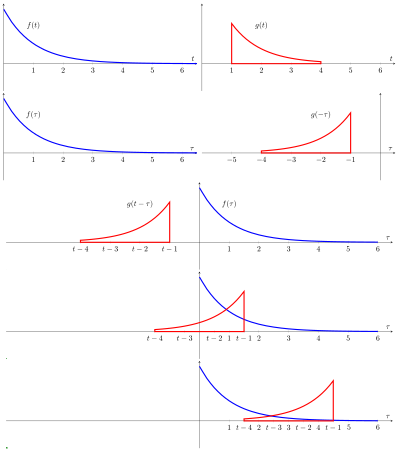${\displaystyle f(t)}$${\displaystyle g(t)}$ ${\displaystyle \int _{-\infty }^{\infty }\delta (\tau )g(t-\tau )\,d\tau =g(t)}$
En este ejemplo, el "pulso" de color rojo es una función par, por lo que la convolución es equivalente a la correlación. Una instantánea de esta "película" muestra las funciones y (en azul) para algún valor de parámetro que se define arbitrariamente como la distancia a lo largo del eje desde el punto hasta el centro del pulso rojo. La cantidad de amarillo es el área del producto calculado por la integral de convolución/correlación. La película se crea cambiando y recalculando continuamente la integral. El resultado (mostrado en negro) es una función de pero se representa gráficamente en el mismo eje para mayor comodidad y comparación.${\displaystyle \ g(\tau ),}$ ${\displaystyle (\ g(-\tau )=g(\tau )\ ),}$${\displaystyle g(t-\tau )}$${\displaystyle f(\tau )}$${\displaystyle t,}$${\displaystyle \tau }$${\displaystyle \tau =0}$${\displaystyle f(\tau )\cdot g(t-\tau ),}$${\displaystyle t}$${\displaystyle t,}$${\displaystyle \tau ,}$
En esta representación, se podría representar la respuesta de un circuito resistor-capacitador a un pulso estrecho que ocurre en En otras palabras, si el resultado de la convolución es justo Pero cuando es el pulso más ancho (en rojo), la respuesta es una versión "manchada" de Comienza en porque lo definimos como la distancia desde el eje hasta el centro del pulso ancho (en lugar del borde delantero).${\displaystyle f(\tau )}$${\displaystyle \tau =0.}$${\displaystyle g(\tau )=\delta (\tau ),}$${\displaystyle f(t).}$${\displaystyle g(\tau )}$${\displaystyle f(t).}$${\displaystyle t=-0.5,}$${\displaystyle t}$${\displaystyle \tau =0}$

Uno de los primeros usos de la integral de convolución apareció en la derivación del teorema de Taylor de D'Alembert en Recherches sur différents points importants du système du monde, publicado en 1754. ^[6]

Además, una expresión del tipo:

${\displaystyle \int f(u)\cdot g(x-u)\,du}$

es utilizado por Sylvestre François Lacroix en la página 505 de su libro titulado Tratado de las diferencias y las series , que es el último de los 3 volúmenes de la serie enciclopédica: Traité du calcul différentiel et du calcul intégral , Chez Courcier, París, 1797-1800. ^[7] Poco después, las operaciones de convolución aparecen en las obras de Pierre Simon Laplace , Jean-Baptiste Joseph Fourier , Siméon Denis Poisson y otros. El término en sí no entró en uso generalizado hasta la década de 1950 o 1960. Antes de eso, a veces se conocía como Faltung (que significa plegado en alemán ), producto de composición , integral de superposición e integral de Carson . ^[8] Sin embargo, aparece ya en 1903, aunque la definición es bastante desconocida en usos más antiguos. ^{[9] [10]}

La operación:

${\displaystyle \int _{0}^{t}\varphi (s)\psi (t-s)\,ds,\quad 0\leq t<\infty ,}$

es un caso particular de productos de composición considerados por el matemático italiano Vito Volterra en 1913. ^[11]

Cuando una función es periódica, con período , entonces para funciones, , tales que existe, la convolución también es periódica e idéntica a:${\displaystyle g_{T}}$${\displaystyle T}$${\displaystyle f}$${\displaystyle f*g_{T}}$

${\displaystyle (f*g_{T})(t)\equiv \int _{t_{0}}^{t_{0}+T}\left[\sum _{k=-\infty }^{\infty }f(\tau +kT)\right]g_{T}(t-\tau )\,d\tau ,}$

donde es una elección arbitraria. La suma se denomina suma periódica de la función .${\displaystyle t_{0}}$${\displaystyle f}$

Cuando es una suma periódica de otra función, , entonces se conoce como una convolución circular o cíclica de y .${\displaystyle g_{T}}$${\displaystyle g}$${\displaystyle f*g_{T}}$${\displaystyle f}$${\displaystyle g}$

Y si la suma periódica anterior se reemplaza por , la operación se llama convolución periódica de y .${\displaystyle f_{T}}$${\displaystyle f_{T}}$${\displaystyle g_{T}}$

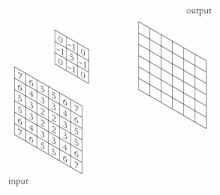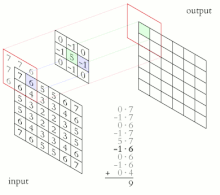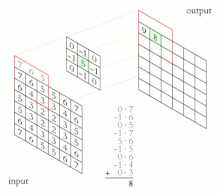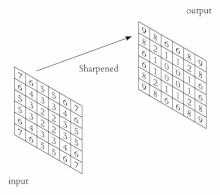
Para funciones de valor complejo y definidas en el conjunto de números enteros, la convolución discreta de y viene dada por: ^[12]${\displaystyle f}$${\displaystyle g}$${\displaystyle \mathbb {Z} }$${\displaystyle f}$${\displaystyle g}$

${\displaystyle (f*g)[n]=\sum _{m=-\infty }^{\infty }f[m]g[n-m],}$

o equivalentemente (ver conmutatividad) por:

${\displaystyle (f*g)[n]=\sum _{m=-\infty }^{\infty }f[n-m]g[m].}$

La convolución de dos secuencias finitas se define extendiendo las secuencias a funciones finitas en el conjunto de números enteros. Cuando las secuencias son los coeficientes de dos polinomios , entonces los coeficientes del producto ordinario de los dos polinomios son la convolución de las dos secuencias originales. Esto se conoce como el producto de Cauchy de los coeficientes de las secuencias.

Por lo tanto, cuando g tiene un soporte finito en el conjunto (lo que representa, por ejemplo, una respuesta de impulso finita ), se puede utilizar una suma finita: ^[13]${\displaystyle \{-M,-M+1,\dots ,M-1,M\}}$

${\displaystyle (f*g)[n]=\sum _{m=-M}^{M}f[n-m]g[m].}$

Cuando una función es periódica, con período entonces para funciones tales que existe, la convolución también es periódica e idéntica a :${\displaystyle g_{_{N}}}$${\displaystyle N,}$${\displaystyle f,}$${\displaystyle f*g_{_{N}}}$

${\displaystyle (f*g_{_{N}})[n]\equiv \sum _{m=0}^{N-1}\left(\sum _{k=-\infty }^{\infty }{f}[m+kN]\right)g_{_{N}}[n-m].}$

La suma de se llama suma periódica de la función.${\displaystyle k}$${\displaystyle f.}$

Si es una suma periódica de otra función, entonces se conoce como convolución circular de y${\displaystyle g_{_{N}}}$${\displaystyle g,}$${\displaystyle f*g_{_{N}}}$${\displaystyle f}$${\displaystyle g.}$

Cuando las duraciones distintas de cero de ambos y están limitadas al intervalo se reducen a estas formas comunes :${\displaystyle f}$${\displaystyle g}$${\displaystyle [0,N-1],}$  ${\displaystyle f*g_{_{N}}}$

${\displaystyle {\begin{aligned}\left(f*g_{N}\right)[n]&=\sum _{m=0}^{N-1}f[m]g_{N}[n-m]\\&=\sum _{m=0}^{n}f[m]g[n-m]+\sum _{m=n+1}^{N-1}f[m]g[N+n-m]\\[2pt]&=\sum _{m=0}^{N-1}f[m]g[(n-m)_{\bmod {N}}]\\[2pt]&\triangleq \left(f*_{N}g\right)[n]\end{aligned}}}$

( Ec.1 )

La notación para convolución cíclica denota convolución sobre el grupo cíclico de números enteros módulo N.${\displaystyle f*_{N}g}$

La convolución circular surge con mayor frecuencia en el contexto de la convolución rápida con un algoritmo de transformada rápida de Fourier (FFT).

En muchas situaciones, las convoluciones discretas se pueden convertir en convoluciones circulares, de modo que se puedan utilizar transformaciones rápidas con una propiedad de convolución para implementar el cálculo. Por ejemplo, la convolución de secuencias de dígitos es la operación principal en la multiplicación de números de varios dígitos, que por lo tanto se puede implementar de manera eficiente con técnicas de transformación (Knuth 1997, §4.3.3.C; von zur Gathen & Gerhard 2003, §8.2).

La ecuación 1 requiere N operaciones aritméticas por valor de salida y N ² operaciones para N salidas. Esto se puede reducir significativamente con cualquiera de varios algoritmos rápidos. El procesamiento de señales digitales y otras aplicaciones suelen utilizar algoritmos de convolución rápidos para reducir el coste de la convolución a una complejidad de O( N log N ).

Los algoritmos de convolución rápida más comunes utilizan algoritmos de transformada rápida de Fourier (FFT) a través del teorema de convolución circular . Específicamente, la convolución circular de dos secuencias de longitud finita se encuentra tomando una FFT de cada secuencia, multiplicando puntualmente y luego realizando una FFT inversa. Las convoluciones del tipo definido anteriormente se implementan de manera eficiente utilizando esa técnica junto con la extensión cero y/o descartando partes de la salida. Otros algoritmos de convolución rápida, como el algoritmo de Schönhage-Strassen o la transformada de Mersenne, ^[14] utilizan transformadas rápidas de Fourier en otros anillos . El método de Winograd se utiliza como una alternativa a la FFT. ^[15] Acelera significativamente la convolución 1D, ^[16] 2D, ^[17] y 3D ^[18] .

Si una secuencia es mucho más larga que la otra, la extensión cero de la secuencia más corta y la convolución circular rápida no es el método computacionalmente más eficiente disponible. ^[19] En cambio, descomponer la secuencia más larga en bloques y convolucionar cada bloque permite algoritmos más rápidos como el método de superposición-guardado y el método de superposición-adición . ^[20] Un método de convolución híbrido que combina algoritmos de bloque y FIR permite una latencia de entrada-salida cero que es útil para cálculos de convolución en tiempo real. ^[21]

La convolución de dos funciones de valor complejo en R ^d es en sí misma una función de valor complejo en R ^d , definida por:

${\displaystyle (f*g)(x)=\int _{\mathbf {R} ^{d}}f(y)g(x-y)\,dy=\int _{\mathbf {R} ^{d}}f(x-y)g(y)\,dy,}$

y está bien definida sólo si f y g decaen lo suficientemente rápido en el infinito para que exista la integral. Las condiciones para la existencia de la convolución pueden ser complicadas, ya que una explosión en g en el infinito puede compensarse fácilmente con un decaimiento suficientemente rápido en f . La cuestión de la existencia puede implicar, por tanto, diferentes condiciones en f y g :

Si f y g son funciones continuas con soporte compacto , entonces existe su convolución, que también tiene soporte compacto y es continua (Hörmander 1983, Capítulo 1). En términos más generales, si una de las funciones (por ejemplo, f ) tiene soporte compacto y la otra es localmente integrable , entonces la convolución f ∗ g está bien definida y es continua.

La convolución de f y g también está bien definida cuando ambas funciones son integrables localmente cuadradas en R y están soportadas en un intervalo de la forma [ a , +∞) (o ambas están soportadas en [−∞, a ] ).

La convolución de f y g existe si f y g son ambas funciones integrables de Lebesgue en L ¹ ( R ^d ) , y en este caso f ∗ g también es integrable (Stein y Weiss 1971, Teorema 1.3). Esto es una consecuencia del teorema de Tonelli . Esto también es cierto para funciones en L ¹ , bajo la convolución discreta, o más generalmente para la convolución en cualquier grupo.

De la misma manera, si f ∈ L ¹ ( R ^d ) y   g ∈ L ^p ( R ^d ) donde 1 ≤ p ≤ ∞ , entonces   f * g ∈ L ^p ( R ^d ), y

${\displaystyle \|{f}*g\|_{p}\leq \|f\|_{1}\|g\|_{p}.}$

En el caso particular p = 1 , esto demuestra que L ¹ es un álgebra de Banach bajo la convolución (y la igualdad de los dos lados se cumple si f y g son no negativos en casi todas partes).

En términos más generales, la desigualdad de Young implica que la convolución es una función bilineal continua entre espacios L ^p adecuados . Específicamente, si 1 ≤ p , q , r ≤ ∞ satisfacen:

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{r}}+1,}$

entonces

${\displaystyle \left\Vert f*g\right\Vert _{r}\leq \left\Vert f\right\Vert _{p}\left\Vert g\right\Vert _{q},\quad f\in L^{p},\ g\in L^{q},}$

de modo que la convolución es una aplicación bilineal continua de L ^p × L ^q a L ^r . La desigualdad de Young para la convolución también es verdadera en otros contextos (grupo de círculos, convolución en Z ). La desigualdad anterior no es nítida en la línea real: cuando 1 < p , q , r < ∞ , existe una constante B _{p , q} < 1 tal que:

${\displaystyle \left\Vert f*g\right\Vert _{r}\leq B_{p,q}\left\Vert f\right\Vert _{p}\left\Vert g\right\Vert _{q},\quad f\in L^{p},\ g\in L^{q}.}$

El valor óptimo de B _{p , q} fue descubierto en 1975 ^[22] e independientemente en 1976, ^[23] véase desigualdad de Brascamp-Lieb .

Una estimación más fuerte es verdadera siempre que 1 < p , q , r < ∞ :

${\displaystyle \|f*g\|_{r}\leq C_{p,q}\|f\|_{p}\|g\|_{q,w}}$

donde es la norma débil L ^q . La convolución también define una función continua bilineal para , debido a la desigualdad débil de Young: ^[24]${\displaystyle \|g\|_{q,w}}$${\displaystyle L^{p,w}\times L^{q,w}\to L^{r,w}}$${\displaystyle 1<p,q,r<\infty }$

${\displaystyle \|f*g\|_{r,w}\leq C_{p,q}\|f\|_{p,w}\|g\|_{r,w}.}$

Además de las funciones con soporte compacto y las funciones integrables, también se pueden convolucionar las funciones que tienen un decaimiento suficientemente rápido en el infinito. Una característica importante de la convolución es que si f y g decaen rápidamente, entonces f ∗ g también decae rápidamente. En particular, si f y g son funciones que decrecen rápidamente , entonces también lo es la convolución f ∗ g . Combinado con el hecho de que la convolución conmuta con la diferenciación (ver #Propiedades), se deduce que la clase de funciones de Schwartz está cerrada bajo convolución (Stein & Weiss 1971, Teorema 3.3).

Si f es una función suave que está soportada de forma compacta y g es una distribución, entonces f ∗ g es una función suave definida por

${\displaystyle \int _{\mathbb {R} ^{d}}{f}(y)g(x-y)\,dy=(f*g)(x)\in C^{\infty }(\mathbb {R} ^{d}).}$

De manera más general, es posible extender la definición de la convolución de una manera única con la misma f anterior, de modo que la ley asociativa${\displaystyle \varphi }$

${\displaystyle f*(g*\varphi )=(f*g)*\varphi }$

sigue siendo válida en el caso en que f es una distribución y g una distribución con soporte compacto (Hörmander 1983, §4.2).

La convolución de dos medidas de Borel cualesquiera μ y ν de variación acotada es la medida definida por (Rudin 1962)${\displaystyle \mu *\nu }$

${\displaystyle \int _{\mathbf {R} ^{d}}f(x)\,d(\mu *\nu )(x)=\int _{\mathbf {R} ^{d}}\int _{\mathbf {R} ^{d}}f(x+y)\,d\mu (x)\,d\nu (y).}$

En particular,

${\displaystyle (\mu *\nu )(A)=\int _{\mathbf {R} ^{d}\times \mathbf {R} ^{d}}1_{A}(x+y)\,d(\mu \times \nu )(x,y),}$

donde es un conjunto medible y es la función indicadora de .${\displaystyle A\subset \mathbf {R} ^{d}}$${\displaystyle 1_{A}}$${\displaystyle A}$

Esto concuerda con la convolución definida anteriormente cuando μ y ν se consideran distribuciones, así como con la convolución de funciones L ¹ cuando μ y ν son absolutamente continuas con respecto a la medida de Lebesgue.

La convolución de medidas también satisface la siguiente versión de la desigualdad de Young

${\displaystyle \|\mu *\nu \|\leq \|\mu \|\|\nu \|}$

donde la norma es la variación total de una medida. Debido a que el espacio de medidas de variación acotada es un espacio de Banach , la convolución de medidas se puede tratar con métodos estándar de análisis funcional que pueden no ser aplicables para la convolución de distribuciones.

La convolución define un producto en el espacio lineal de funciones integrables. Este producto satisface las siguientes propiedades algebraicas, que formalmente significan que el espacio de funciones integrables con el producto dado por la convolución es un álgebra asociativa conmutativa sin identidad (Strichartz 1994, §3.3). Otros espacios lineales de funciones, como el espacio de funciones continuas de soporte compacto, son cerrados bajo la convolución y, por lo tanto, también forman álgebras asociativas conmutativas.

Conmutatividad

$${\displaystyle f*g=g*f}$$Demostración: Por definición: Cambiando la variable de integración al resultado se sigue.$${\displaystyle (f*g)(t)=\int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau }$$${\displaystyle u=t-\tau }$

Asociatividad

$${\displaystyle f*(g*h)=(f*g)*h}$$Demostración: Esto se deduce del uso del teorema de Fubini (es decir, las integrales dobles pueden evaluarse como integrales iteradas en cualquier orden).

Distributividad

$${\displaystyle f*(g+h)=(f*g)+(f*h)}$$Demostración: Esto se deduce de la linealidad de la integral.

Asociatividad con multiplicación escalar

$${\displaystyle a(f*g)=(af)*g}$$para cualquier número real (o complejo) .${\displaystyle a}$

Identidad multiplicativa

Ningún álgebra de funciones posee una identidad para la convolución. La falta de identidad no suele ser un inconveniente importante, ya que la mayoría de las colecciones de funciones en las que se realiza la convolución pueden convolucionarse con una distribución delta (un impulso unitario, centrado en cero) o, como mínimo (como es el caso de L ¹ ) admiten aproximaciones a la identidad . Sin embargo, el espacio lineal de distribuciones con soporte compacto admite una identidad bajo la convolución. Específicamente, donde δ es la distribución delta.$${\displaystyle f*\delta =f}$$

Elemento inverso

Algunas distribuciones S tienen un elemento inverso S ⁻¹ para la convolución que luego debe satisfacer, a partir de lo cual se puede obtener una fórmula explícita para S ^{−1 .}$${\displaystyle S^{-1}*S=\delta }$$

El conjunto de distribuciones invertibles forma un grupo abeliano bajo la convolución.

Conjugación compleja

$${\displaystyle {\overline {f*g}}={\overline {f}}*{\overline {g}}}$$

Inversión del tiempo

Si     entonces  ${\displaystyle q(t)=r(t)*s(t),}$${\displaystyle q(-t)=r(-t)*s(-t).}$

Prueba (usando el teorema de convolución ):

${\displaystyle q(t)\ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ Q(f)=R(f)S(f)}$

${\displaystyle q(-t)\ {\stackrel {\mathcal {F}}{\Longleftrightarrow }}\ \ Q(-f)=R(-f)S(-f)}$

${\displaystyle {\begin{aligned}q(-t)&={\mathcal {F}}^{-1}{\bigg \{}R(-f)S(-f){\bigg \}}\\&={\mathcal {F}}^{-1}{\bigg \{}R(-f){\bigg \}}*{\mathcal {F}}^{-1}{\bigg \{}S(-f){\bigg \}}\\&=r(-t)*s(-t)\end{aligned}}}$

Relación con la diferenciación

$${\displaystyle (f*g)'=f'*g=f*g'}$$Prueba:

${\displaystyle {\begin{aligned}(f*g)'&={\frac {d}{dt}}\int _{-\infty }^{\infty }f(\tau )g(t-\tau )\,d\tau \\&=\int _{-\infty }^{\infty }f(\tau ){\frac {\partial }{\partial t}}g(t-\tau )\,d\tau \\&=\int _{-\infty }^{\infty }f(\tau )g'(t-\tau )\,d\tau =f*g'.\end{aligned}}}$

Relación con la integración

Si y entonces${\textstyle F(t)=\int _{-\infty }^{t}f(\tau )d\tau ,}$${\textstyle G(t)=\int _{-\infty }^{t}g(\tau )\,d\tau ,}$$${\displaystyle (F*g)(t)=(f*G)(t)=\int _{-\infty }^{t}(f*g)(\tau )\,d\tau .}$$

Si f y g son funciones integrables, entonces la integral de su convolución en todo el espacio se obtiene simplemente como el producto de sus integrales: ^[25]

${\displaystyle \int _{\mathbf {R} ^{d}}(f*g)(x)\,dx=\left(\int _{\mathbf {R} ^{d}}f(x)\,dx\right)\left(\int _{\mathbf {R} ^{d}}g(x)\,dx\right).}$

Esto se desprende del teorema de Fubini . El mismo resultado se cumple si se supone que f y g son funciones mensurables no negativas, según el teorema de Tonelli .

En el caso de una variable,

${\displaystyle {\frac {d}{dx}}(f*g)={\frac {df}{dx}}*g=f*{\frac {dg}{dx}}}$

donde es la derivada . De manera más general, en el caso de funciones de varias variables, se cumple una fórmula análoga con la derivada parcial :${\displaystyle {\frac {d}{dx}}}$

${\displaystyle {\frac {\partial }{\partial x_{i}}}(f*g)={\frac {\partial f}{\partial x_{i}}}*g=f*{\frac {\partial g}{\partial x_{i}}}.}$

Una consecuencia particular de esto es que la convolución puede verse como una operación de "suavizado": la convolución de f y g es diferenciable tantas veces como f y g lo sean en total.

Estas identidades se cumplen, por ejemplo, bajo la condición de que f y g sean absolutamente integrables y al menos una de ellas tenga una derivada débil absolutamente integrable (L ¹ ), como consecuencia de la desigualdad de convolución de Young . Por ejemplo, cuando f es continuamente diferenciable con soporte compacto y g es una función arbitraria localmente integrable,

${\displaystyle {\frac {d}{dx}}(f*g)={\frac {df}{dx}}*g.}$

Estas identidades también se cumplen de manera mucho más amplia en el sentido de distribuciones templadas si una de f o g es una distribución templada de rápida disminución , una distribución templada con soporte compacto o una función de Schwartz y la otra es una distribución templada. Por otro lado, dos funciones integrables positivas e infinitamente diferenciables pueden tener una convolución continua en ninguna parte.

En el caso discreto, el operador de diferencia D f ( n ) = f ( n + 1) − f ( n ) satisface una relación análoga:

${\displaystyle D(f*g)=(Df)*g=f*(Dg).}$

El teorema de convolución establece que ^[26]

${\displaystyle {\mathcal {F}}\{f*g\}={\mathcal {F}}\{f\}\cdot {\mathcal {F}}\{g\}}$

donde denota la transformada de Fourier de .${\displaystyle {\mathcal {F}}\{f\}}$${\displaystyle f}$

Versiones de este teorema también son válidas para la transformada de Laplace , la transformada de Laplace de dos lados , la transformada Z y la transformada de Mellin .

Si es la matriz de transformada de Fourier , entonces${\displaystyle {\mathcal {W}}}$

${\displaystyle {\mathcal {W}}\left(C^{(1)}x\ast C^{(2)}y\right)=\left({\mathcal {W}}C^{(1)}\bullet {\mathcal {W}}C^{(2)}\right)(x\otimes y)={\mathcal {W}}C^{(1)}x\circ {\mathcal {W}}C^{(2)}y}$,

donde es el producto de división de caras , ^{[27] [28] [29] [30] [31]} denota el producto de Kronecker , denota el producto de Hadamard (este resultado es una evolución de las propiedades del bosquejo de conteo ^[32] ).${\displaystyle \bullet }$ ${\displaystyle \otimes }$${\displaystyle \circ }$

Esto se puede generalizar para matrices apropiadas :${\displaystyle \mathbf {A} ,\mathbf {B} }$

${\displaystyle {\mathcal {W}}\left((\mathbf {A} x)\ast (\mathbf {B} y)\right)=\left(({\mathcal {W}}\mathbf {A} )\bullet ({\mathcal {W}}\mathbf {B} )\right)(x\otimes y)=({\mathcal {W}}\mathbf {A} x)\circ ({\mathcal {W}}\mathbf {B} y)}$

de las propiedades del producto que parte la cara .

La convolución conmuta con las traslaciones, lo que significa que

${\displaystyle \tau _{x}(f*g)=(\tau _{x}f)*g=f*(\tau _{x}g)}$

donde τ _x f es la traslación de la función f por x definida por

${\displaystyle (\tau _{x}f)(y)=f(y-x).}$

Si f es una función de Schwartz , entonces τ _x f es la convolución con una función delta de Dirac trasladada τ _x f = f ∗ τ _x δ . Por lo tanto, la invariancia de la traslación de la convolución de las funciones de Schwartz es una consecuencia de la asociatividad de la convolución.

Además, en determinadas condiciones, la convolución es la operación de traducción invariante más general. En términos informales, se cumple lo siguiente:

Supóngase que S es un operador lineal acotado que actúa sobre funciones que conmutan con traslaciones: S ( τ _x f ) = τ _x ( Sf ) para todo x . Entonces S se da como convolución con una función (o distribución) g _S ; es decir Sf = g _S ∗ f .

Por lo tanto, algunas operaciones invariantes de traslación pueden representarse como convolución. Las convoluciones desempeñan un papel importante en el estudio de sistemas invariantes en el tiempo , y especialmente en la teoría de sistemas LTI . La función representativa g _S es la respuesta al impulso de la transformación S .

Una versión más precisa del teorema citado anteriormente requiere especificar la clase de funciones en las que se define la convolución, y también requiere suponer además que S debe ser un operador lineal continuo con respecto a la topología apropiada . Se sabe, por ejemplo, que todo operador lineal continuo invariante de traslación continua sobre L ^{1 es la convolución con una} medida de Borel finita . De manera más general, todo operador lineal continuo invariante de traslación continua sobre L ^p para 1 ≤ p < ∞ es la convolución con una distribución templada cuya transformada de Fourier está acotada. Es decir, todos están dados por multiplicadores de Fourier acotados .

Si G es un grupo adecuado dotado de una medida λ, y si f y g son funciones integrables reales o complejas en G , entonces podemos definir su convolución por

${\displaystyle (f*g)(x)=\int _{G}f(y)g\left(y^{-1}x\right)\,d\lambda (y).}$

En general, no es conmutativa. En casos típicos de interés, G es un grupo topológico localmente compacto de Hausdorff y λ es una medida de Haar (izquierda) . En ese caso, a menos que G sea unimodular , la convolución definida de esta manera no es la misma que . La preferencia de una sobre la otra se realiza de modo que la convolución con una función fija g conmute con la traslación izquierda en el grupo:${\textstyle \int f\left(xy^{-1}\right)g(y)\,d\lambda (y)}$

${\displaystyle L_{h}(f*g)=(L_{h}f)*g.}$

Además, la convención también es necesaria para mantener la coherencia con la definición de la convolución de medidas que se da a continuación. Sin embargo, con una medida de Haar derecha en lugar de izquierda, se prefiere la última integral a la primera.

En los grupos abelianos localmente compactos , se cumple una versión del teorema de convolución : la transformada de Fourier de una convolución es el producto puntual de las transformadas de Fourier. El grupo circular T con la medida de Lebesgue es un ejemplo inmediato. Para una g fija en L ¹ ( T ), tenemos el siguiente operador familiar que actúa sobre el espacio de Hilbert L ² ( T ):

${\displaystyle T{f}(x)={\frac {1}{2\pi }}\int _{\mathbf {T} }{f}(y)g(x-y)\,dy.}$

El operador T es compacto . Un cálculo directo muestra que su adjunto T* es convolución con

${\displaystyle {\bar {g}}(-y).}$

Por la propiedad de conmutatividad citada anteriormente, T es normal : T * T = TT * . Además, T conmuta con los operadores de traslación. Considere la familia S de operadores que consiste en todas esas convoluciones y los operadores de traslación. Entonces S es una familia conmutativa de operadores normales. Según la teoría espectral , existe una base ortonormal { h _k } que diagonaliza simultáneamente a S . Esto caracteriza a las convoluciones en el círculo. Específicamente, tenemos

${\displaystyle h_{k}(x)=e^{ikx},\quad k\in \mathbb {Z} ,\;}$

que son precisamente los caracteres de T . Cada convolución es un operador de multiplicación compacto en esta base. Esto puede verse como una versión del teorema de convolución discutido anteriormente.

Un ejemplo discreto es un grupo cíclico finito de orden n . Los operadores de convolución se representan aquí mediante matrices circulantes y se pueden diagonalizar mediante la transformada de Fourier discreta .

Un resultado similar se aplica a los grupos compactos (no necesariamente abelianos): los coeficientes matriciales de representaciones unitarias de dimensión finita forman una base ortonormal en L ² según el teorema de Peter-Weyl , y un análogo del teorema de convolución sigue siendo válido, junto con muchos otros aspectos del análisis armónico que dependen de la transformada de Fourier.

Sea G un grupo topológico (escrito multiplicativamente). Si μ y ν son medidas de Borel finitas en G , entonces su convolución μ ∗ ν se define como la medida de empuje hacia delante de la acción del grupo y se puede escribir como

${\displaystyle (\mu *\nu )(E)=\iint 1_{E}(xy)\,d\mu (x)\,d\nu (y)}$

para cada subconjunto medible E de G . La convolución es también una medida finita, cuya variación total satisface

${\displaystyle \|\mu *\nu \|\leq \left\|\mu \right\|\left\|\nu \right\|.}$

En el caso en que G es localmente compacto con medida de Haar (izquierda) λ, y μ y ν son absolutamente continuos con respecto a λ, de modo que cada uno tiene una función de densidad , entonces la convolución μ∗ν también es absolutamente continua, y su función de densidad es simplemente la convolución de las dos funciones de densidad separadas.

Si μ y ν son medidas de probabilidad en el grupo topológico ( R ,+), entonces la convolución μ ∗ ν es la distribución de probabilidad de la suma X + Y de dos variables aleatorias independientes X e Y cuyas distribuciones respectivas son μ y ν.

En el análisis convexo , la convolución infimal de funciones convexas propias (no idénticas ) en se define por: ^[33] Se puede demostrar que la convolución infimal de funciones convexas es convexa. Además, satisface una identidad análoga a la de la transformada de Fourier de una convolución tradicional, en la que el papel de la transformada de Fourier lo desempeña la transformada de Legendre : Tenemos:${\displaystyle +\infty }$ ${\displaystyle f_{1},\dots ,f_{m}}$${\displaystyle \mathbb {R} ^{n}}$$${\displaystyle (f_{1}*\cdots *f_{m})(x)=\inf _{x}\{f_{1}(x_{1})+\cdots +f_{m}(x_{m})|x_{1}+\cdots +x_{m}=x\}.}$$$${\displaystyle \varphi ^{*}(x)=\sup _{y}(x\cdot y-\varphi (y)).}$$$${\displaystyle (f_{1}*\cdots *f_{m})^{*}(x)=f_{1}^{*}(x)+\cdots +f_{m}^{*}(x).}$$

Sea ( X , Δ, ∇, ε , η ) una biálgebra con comultiplicación Δ, multiplicación ∇, unidad η y counit ε . La convolución es un producto definido en el álgebra de endomorfismos End( X ) de la siguiente manera. Sean φ , ψ ∈ End( X ), es decir, φ , ψ : X → X funciones que respetan toda la estructura algebraica de X , entonces la convolución φ ∗ ψ se define como la composición

${\displaystyle X\mathrel {\xrightarrow {\Delta } } X\otimes X\mathrel {\xrightarrow {\phi \otimes \psi } } X\otimes X\mathrel {\xrightarrow {\nabla } } X.}$

La convolución aparece notablemente en la definición de álgebras de Hopf (Kassel 1995, §III.3). Una biálgebra es un álgebra de Hopf si y sólo si tiene un antípoda: un endomorfismo S tal que

${\displaystyle S*\operatorname {id} _{X}=\operatorname {id} _{X}*S=\eta \circ \varepsilon .}$

La convolución y operaciones relacionadas se encuentran en muchas aplicaciones en ciencia, ingeniería y matemáticas.

• Las redes neuronales convolucionales aplican múltiples núcleos de convolución en cascada con aplicaciones en visión artificial e inteligencia artificial . ^{[34] [35]} Aunque en realidad se trata de correlaciones cruzadas en lugar de convoluciones en la mayoría de los casos. ^[36]
• En el procesamiento de imágenes no basado en redes neuronales
  • En el procesamiento de imágenes digitales, el filtrado convolucional juega un papel importante en muchos algoritmos importantes en la detección de bordes y procesos relacionados (ver Kernel (procesamiento de imágenes) ).
  • En óptica , una fotografía desenfocada es una convolución de la imagen nítida con una función de lente. El término fotográfico para esto es bokeh .
  • En aplicaciones de procesamiento de imágenes, como agregar desenfoque.
• En el procesamiento de datos digitales
  • En química analítica , los filtros de suavizado Savitzky-Golay se utilizan para el análisis de datos espectroscópicos. Pueden mejorar la relación señal-ruido con una distorsión mínima de los espectros.
  • En estadística , una media móvil ponderada es una convolución.
• En acústica , la reverberación es la convolución del sonido original con ecos de los objetos que rodean la fuente del sonido.
  • En el procesamiento de señales digitales, se utiliza la convolución para mapear la respuesta al impulso de una sala real en una señal de audio digital.
  • En la música electrónica, la convolución es la imposición de una estructura espectral o rítmica a un sonido. A menudo, esta envolvente o estructura se toma de otro sonido. La convolución de dos señales es el filtrado de una a través de la otra. ^[37]
• En ingeniería eléctrica , la convolución de una función (la señal de entrada ) con una segunda función (la respuesta al impulso) da como resultado un sistema lineal invariante en el tiempo (LTI). En cualquier momento dado, el resultado es un efecto acumulado de todos los valores anteriores de la función de entrada, y los valores más recientes suelen tener la mayor influencia (expresada como un factor multiplicativo). La función de respuesta al impulso proporciona ese factor como una función del tiempo transcurrido desde que se produjo cada valor de entrada.
• En física , siempre que hay un sistema lineal con un " principio de superposición ", aparece una operación de convolución. Por ejemplo, en espectroscopia , el ensanchamiento de línea debido al efecto Doppler por sí solo da una forma de línea espectral gaussiana y el ensanchamiento por colisión por sí solo da una forma de línea lorentziana . Cuando ambos efectos están en funcionamiento, la forma de la línea es una convolución de Gauss y Lorentziana, una función de Voigt .
  • En la espectroscopia de fluorescencia resuelta en el tiempo , la señal de excitación puede tratarse como una cadena de pulsos delta, y la fluorescencia medida es una suma de desintegraciones exponenciales de cada pulso delta.
  • En dinámica de fluidos computacional , el modelo de turbulencia de simulación de grandes remolinos (LES) utiliza la operación de convolución para reducir el rango de escalas de longitud necesarias en el cálculo, reduciendo así el costo computacional.
• En teoría de probabilidad , la distribución de probabilidad de la suma de dos variables aleatorias independientes es la convolución de sus distribuciones individuales.
  • En la estimación de densidad de kernel , una distribución se estima a partir de puntos de muestra mediante convolución con un kernel, como un gaussiano isótropo. ^[38]
• En los sistemas de planificación de tratamientos de radioterapia, la mayor parte de todos los códigos de cálculo modernos aplican un algoritmo de superposición de convolución. ^{[ aclaración necesaria ]}
• En confiabilidad estructural, el índice de confiabilidad se puede definir con base en el teorema de convolución.
  • La definición del índice de fiabilidad para funciones de estado límite con distribuciones no normales se puede establecer a partir de la función de distribución conjunta . De hecho, la función de distribución conjunta se puede obtener utilizando la teoría de convolución. ^[39]
• En la hidrodinámica de partículas suavizadas , las simulaciones de la dinámica de fluidos se calculan utilizando partículas, cada una con núcleos circundantes. Para cualquier partícula dada , se calcula alguna cantidad física como una convolución de con una función de ponderación, donde denota los vecinos de la partícula : aquellos que se encuentran dentro de su núcleo. La convolución se aproxima como una suma sobre cada vecino. ^[40]${\displaystyle i}$${\displaystyle A_{i}}$${\displaystyle A_{j}}$${\displaystyle j}$${\displaystyle i}$
• En el cálculo fraccional, la convolución es fundamental en varias definiciones de integral fraccional y derivada fraccional.

• Bracewell, R. (1986), La transformada de Fourier y sus aplicaciones (2.ª ed.), McGraw–Hill, ISBN 0-07-116043-4.
• Damelin, S.; Miller, W. (2011), Las matemáticas del procesamiento de señales , Cambridge University Press, ISBN 978-1107601048
• Diggle, PJ (1985), "Un método de núcleo para suavizar datos de procesos puntuales", Journal of the Royal Statistical Society, Serie C , 34 (2): 138–147, doi :10.2307/2347366, JSTOR  2347366, S2CID  116746157
• Dominguez-Torres, Alejandro (2 de noviembre de 2010). "Origen e historia de la convolución". 41 págs. https://slideshare.net/Alexdfar/origin-adn-history-of-convolution. Cranfield, Bedford MK43 OAL, Reino Unido. Consultado el 13 de marzo de 2013.
• Ghasemi, S. Hooman; Nowak, Andrzej S. (2017), "Índice de confiabilidad para distribuciones no normales de funciones de estado límite", Ingeniería estructural y mecánica , 62 (3): 365–372, doi :10.12989/sem.2017.62.3.365
• Grinshpan, AZ (2017), "Una desigualdad para convoluciones múltiples con respecto a la medida de probabilidad de Dirichlet", Advances in Applied Mathematics , 82 (1): 102–119, doi : 10.1016/j.aam.2016.08.001
• Hewitt, Edwin; Ross, Kenneth A. (1979), Análisis armónico abstracto. vol. I , Grundlehren der Mathematischen Wissenschaften [Principios fundamentales de las ciencias matemáticas], vol. 115 (2ª ed.), Berlín, Nueva York: Springer-Verlag , ISBN 978-3-540-09434-0, Sr.  0551496.
• Hewitt, Edwin; Ross, Kenneth A. (1970), Análisis armónico abstracto. vol. II: Estructura y análisis de grupos compactos. Análisis de grupos abelianos localmente compactos , Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlín, Nueva York: Springer-Verlag , MR  0262773.
• Hörmander, L. (1983), El análisis de operadores diferenciales parciales lineales I , Grundl. Matemáticas. Wissenschaft., vol. 256, Springer, doi :10.1007/978-3-642-96750-4, ISBN 3-540-12104-8, Sr.  0717035.
• Kassel, Christian (1995), Grupos cuánticos , Textos de posgrado en matemáticas, vol. 155, Berlín, Nueva York: Springer-Verlag , doi :10.1007/978-1-4612-0783-2, ISBN 978-0-387-94370-1, Sr.  1321145.
• Knuth, Donald (1997), Algoritmos seminuméricos (3.ª ed.), Reading, Massachusetts: Addison–Wesley, ISBN 0-201-89684-2.
• Narici, Lawrence; Beckenstein, Edward (2011). Espacios vectoriales topológicos . Matemáticas puras y aplicadas (segunda edición). Boca Raton, FL: CRC Press. ISBN 978-1584888666.OCLC 144216834  .
• Reed, Michael; Simon, Barry (1975), Métodos de la física matemática moderna. II. Análisis de Fourier, autoadjunción , Nueva York-Londres: Academic Press Harcourt Brace Jovanovich, Publishers, pp. xv+361, ISBN 0-12-585002-6, Sr.  0493420
• Rudin, Walter (1962), Análisis de Fourier en grupos , Interscience Tracts in Pure and Applied Mathematics, vol. 12, Nueva York–Londres: Interscience Publishers, ISBN 0-471-52364-X, Sr.  0152834.
• Schaefer, Helmut H. ; Wolff, Manfred P. (1999). Espacios vectoriales topológicos . GTM . Vol. 8 (Segunda ed.). Nueva York, NY: Springer New York Imprenta Springer. ISBN 978-1-4612-7155-0.OCLC 840278135  .
• Stein, Elias ; Weiss, Guido (1971), Introducción al análisis de Fourier en espacios euclidianos , Princeton University Press, ISBN 0-691-08078-X.
• Sobolev, VI (2001) [1994], "Convolución de funciones", Enciclopedia de Matemáticas , EMS Press.
• Strichartz, R. (1994), Una guía para la teoría de la distribución y las transformadas de Fourier , CRC Press, ISBN 0-8493-8273-4.
• Titchmarsh, E (1948), Introducción a la teoría de las integrales de Fourier (2.ª ed.), Nueva York, NY: Chelsea Pub. Co. (publicado en 1986), ISBN 978-0-8284-0324-5.
• Trèves, François (2006) [1967]. Espacios vectoriales topológicos, distribuciones y núcleos . Mineola, Nueva York: Publicaciones de Dover. ISBN 978-0-486-45352-1.OCLC 853623322  .
• Uludag, AM (1998), "Sobre el posible deterioro de la suavidad bajo la operación de convolución", J. Math. Anal. Appl. , 227 (2): 335–358, doi : 10.1006/jmaa.1998.6091
• von zur Gathen, J.; Gerhard, J. (2003), Álgebra informática moderna , Cambridge University Press, ISBN 0-521-82646-2.

Busque convolución en Wikcionario, el diccionario libre.

Wikimedia Commons tiene medios relacionados con Convolución .

• Primeros usos: La entrada sobre convolución tiene cierta información histórica.
• Convolución, en el libro The Data Analysis Brief
• https://jhu.edu/~signals/convolve/index.html Applet de Java de convolución visual
• Applet Java de convolución visual para funciones de tiempo discreto
• Calculadora en línea de convolución discreta https://get-the-solution.net/projects/discret-convolution
• https://lpsa.swarthmore.edu/Convolution/CI.html Demostración y visualización de convolución en JavaScript
• https://phiresky.github.io/convolution-demo/ Otra demostración de convolución en JavaScript
• Lecciones sobre procesamiento de imágenes: una colección de 18 lecciones en formato PDF de la Universidad de Vanderbilt. La lección 7 trata sobre convolución 2D, a cargo de Alan Peters
• https://archive.org/details/Lectures_on_Image_Processing
• Tutorial interactivo de la operación de máscara de núcleo de convolución
• Convolución en MathWorld
• Procesador de respuesta a impulsos Freeverb3: procesador de respuesta a impulsos de latencia cero de código abierto con complementos VST
• Demostración Flash interactiva de CS 178 de la Universidad de Stanford que muestra cómo funciona la convolución espacial.
• Una videoconferencia sobre el tema de la convolución impartida por Salman Khan
• Ejemplo de convolución FFT para reconocimiento de patrones (procesamiento de imágenes)
• Guía intuitiva sobre la convolución Una publicación de blog sobre una interpretación intuitiva de la convolución.