Gran gran estrella de 120 celdas
| Gran gran estrella de 120 celdas | |
|---|---|
 Proyección ortogonal | |
| Tipo | Policorono de Schläfli-Hess |
| Células | 120 {5/2,3} |
| Caras | 720 {5/2} |
| Bordes | 1200 |
| Vértices | 600 |
| Figura de vértice | {3,3} |
| Símbolo de Schläfli | {5/2,3,3} |
| Diagrama de Coxeter-Dynkin |          |
| Grupo de simetría | H 4 , [3,3,5] |
| Dual | Gran 600 celdas |
| Propiedades | Regular |

En geometría , el gran polidodecaedro estrellado de 120 celdas o gran polidodecaedro estrellado es un politopo regular de 4 estrellas con símbolo de Schläfli {5/2,3,3}, uno de los 10 politopos regulares de Schläfli-Hess. Es único entre los 10 por tener 600 vértices y tiene la misma disposición de vértices que el polidodecaedro regular convexo de 120 celdas .
Es una de las cuatro estrellas policoras regulares descubiertas por Ludwig Schläfli . Su nombre fue dado por John Horton Conway , extendiendo el sistema de nombres de Arthur Cayley para los sólidos de Kepler-Poinsot , y es la única que contiene los tres modificadores en el nombre.
Imágenes
| H4 | A2 / B3 | A3 / B2 |
|---|---|---|
| Gran estrella de 120 celdas, {5/2,3,3} | ||
 |  |  |
| [10] | [6] | [4] |
| 120 celdas, {5,3,3} | ||
 | 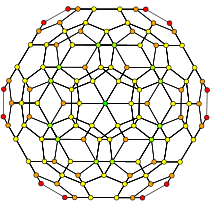 | 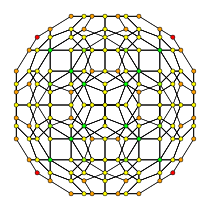 |
Como una estelación
El gran policoron estelado de 120 celdas es la estelación final del policoron estelado de 120 celdas y es el único policoron estelado de Schläfli-Hess que tiene la celda estelada de 120 celdas como envoltura convexa. En este sentido, es análogo al gran dodecaedro estelado tridimensional , que es la estelación final del dodecaedro y el único poliedro de Kepler-Poinsot que tiene el dodecaedro como envoltura convexa. De hecho, el gran policoron estelado de 120 celdas es dual del gran policoronado de 600 celdas , que podría tomarse como un análogo en 4D del gran icosaedro , dual del gran dodecaedro estelado.
Los bordes de la gran estrella de 120 células tienen una longitud τ 6 veces mayor que los del núcleo de 120 células en la profundidad del policoronte, y una longitud τ 3 mayor que la de la pequeña estrella de 120 células en la profundidad del policoronte.
Véase también
- Lista de politopos regulares
- 4-politopo regular convexo – Conjunto de policoras regulares convexas
- Sólidos de Kepler-Poinsot : poliedro estelar regular
- Polígono estrellado – polígonos estrellados regulares
Referencias
- Edmund Hess , (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder [1].
- HSM Coxeter , Politopos regulares , 3.ª ed., Dover Publications, 1973. ISBN 0-486-61480-8 .
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Capítulo 26, Politopos estelares regulares, págs. 404-408)
- Klitzing, Richard. "Polítopos uniformes 4D (policoros) o3o3o5/2x - gogishi".
Enlaces externos
- Polychora regular Archivado el 6 de septiembre de 2003 en Wayback Machine.
- Discusión sobre nombres
- Politopo regular
- La estrella regular Polychora
- Modelo Zome de la estelación final de las 120 celdas Archivado el 10 de octubre de 2022 en Wayback Machine.