Factorial

Factoriales seleccionados; los valores en notación científica están redondeados

${\estilo de visualización n}$	${\estilo de visualización n!}$
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5 040
8	40 320
9	362 880
10	3 628 800
11	39 916 800
12	479 001 600
13	6 227 020 800
14	87 178 291 200
15	1 307 674 368 000
16	20 922 789 888 000
17	355 687 428 096 000
18	6 402 373 705 728 000
19	121 645 100 408 832 000
20	2 432 902 008 176 640 000
25	1.551 121 004 × 10 25
50	3.041 409 320 × 10 64
70	1.197 857 167 × 10 100
100	9.332 621 544 × 10 157
450	1.733 368 733 × 10 1 000
1 000	4.023 872 601 × 10 2 567
3 249	6.412 337 688 × 10 10 000
10 000	2.846 259 681 × 10 35 659
25 206	1.205 703 438 × 10 100 000
100 000	2.824 229 408 × 10 456 573
205 023	2.503 898 932 × 10 1 000 004
1 000 000	8.263 931 688 × 10 5 565 708
10 100	1010 101.998 109 775 4820

En matemáticas , el factorial de un entero ${\estilo de visualización n}$ no negativo , denotado por ,${\estilo de visualización n!}$ es el producto de todos los enteros positivos menores o iguales a .${\estilo de visualización n}$ El factorial de${\estilo de visualización n}$ también es igual al producto de con el factorial inmediatamente inferior: Por ejemplo, El valor de 0! es 1, según la convención para un producto vacío . ^[1]${\estilo de visualización n}$$${\displaystyle {\begin{aligned}n!&=n\veces (n-1)\veces (n-2)\veces (n-3)\veces \cdots \veces 3\veces 2\veces 1\\&=n\veces (n-1)!\\\end{aligned}}}$$$${\displaystyle 5!=5\veces 4!=5\veces 4\veces 3\veces 2\veces 1=120.}$$

Los factoriales se han descubierto en varias culturas antiguas, en particular en las matemáticas indias en las obras canónicas de la literatura jainista , y por los místicos judíos en el libro talmúdico Sefer Yetzirah . La operación factorial se encuentra en muchas áreas de las matemáticas, en particular en la combinatoria , donde su uso más básico cuenta las posibles secuencias distintas (las permutaciones ) de objetos distintos: hay . En el análisis matemático , los factoriales se utilizan en series de potencias para la función exponencial y otras funciones, y también tienen aplicaciones en álgebra , teoría de números , teoría de la probabilidad y ciencias de la computación .${\estilo de visualización n}$${\estilo de visualización n!}$

Gran parte de las matemáticas de la función factorial se desarrollaron a finales del siglo XVIII y principios del XIX. La aproximación de Stirling proporciona una aproximación precisa al factorial de números grandes, mostrando que crece más rápidamente que el crecimiento exponencial . La fórmula de Legendre describe los exponentes de los números primos en una factorización prima de los factoriales, y se puede utilizar para contar los ceros finales de los factoriales. Daniel Bernoulli y Leonhard Euler interpolaron la función factorial a una función continua de números complejos , excepto en los enteros negativos, la función gamma (desplazada) .

Muchas otras funciones y secuencias numéricas notables están estrechamente relacionadas con los factoriales, incluidos los coeficientes binomiales , los factoriales dobles , los factoriales descendentes , los primoriales y los subfactoriales . Las implementaciones de la función factorial se utilizan comúnmente como un ejemplo de diferentes estilos de programación informática y se incluyen en calculadoras científicas y bibliotecas de software de computación científica. Aunque calcular directamente factoriales grandes utilizando la fórmula del producto o la recurrencia no es eficiente, se conocen algoritmos más rápidos, que coinciden con un factor constante en el tiempo para algoritmos de multiplicación rápida para números con la misma cantidad de dígitos.

El concepto de factoriales ha surgido de forma independiente en muchas culturas:

• En matemáticas indias , una de las primeras descripciones conocidas de factoriales proviene del Anuyogadvāra-sūtra, ^[2] una de las obras canónicas de la literatura jainista , a la que se le han asignado fechas que varían desde el 300 a. C. hasta el 400 d. C. ^[3] Separa el orden ordenado e invertido de un conjunto de elementos de los otros órdenes ("mixtos"), evaluando el número de órdenes mixtos restando dos de la fórmula habitual del producto para el factorial. La regla del producto para permutaciones también fue descrita por el monje jainista del siglo VI d. C. Jinabhadra . ^[2] Los eruditos hindúes han estado usando fórmulas factoriales desde al menos 1150, cuando Bhāskara II mencionó los factoriales en su obra Līlāvatī , en relación con un problema de cuántas maneras podía Vishnu sostener sus cuatro objetos característicos (una caracola , un disco , una maza y una flor de loto ) en sus cuatro manos, y un problema similar para un dios de diez manos. ^[4]
• En las matemáticas de Oriente Medio, el libro místico hebreo de la creación Sefer Yetzirah , del periodo talmúdico (200 a 500 d. C.), enumera factoriales de hasta 7! como parte de una investigación sobre el número de palabras que se pueden formar a partir del alfabeto hebreo . ^{[5] [6]} Los factoriales también fueron estudiados por razones similares por el gramático árabe del siglo VIII Al-Khalil ibn Ahmad al-Farahidi . ^[5] El matemático árabe Ibn al-Haytham (también conocido como Alhazen, c. 965 - c. 1040) fue el primero en formular el teorema de Wilson que conecta los factoriales con los números primos . ^[7]
• En Europa, aunque las matemáticas griegas incluían algo de combinatoria, y Platón utilizó 5.040 (un factorial) como la población de una comunidad ideal, en parte debido a sus propiedades de divisibilidad, ^[8] no hay evidencia directa de un estudio griego antiguo de los factoriales. En cambio, el primer trabajo sobre factoriales en Europa fue realizado por eruditos judíos como Shabbethai Donnolo , explicando el pasaje del Sefer Yetzirah. ^[9] En 1677, el autor británico Fabian Stedman describió la aplicación de los factoriales al cambio de timbre , un arte musical que implica el sonido de varias campanas afinadas. ^{[10] [11]}

Desde finales del siglo XV en adelante, los factoriales se convirtieron en objeto de estudio por parte de los matemáticos occidentales. En un tratado de 1494, el matemático italiano Luca Pacioli calculó factoriales hasta 11!, en relación con un problema de arreglos de mesas de comedor. ^[12] Christopher Clavius ​​analizó los factoriales en un comentario de 1603 sobre el trabajo de Johannes de Sacrobosco , y en la década de 1640, el polímata francés Marin Mersenne publicó grandes (pero no del todo correctas) tablas de factoriales, hasta 64!, basadas en el trabajo de Clavius. ^[13] La serie de potencias para la función exponencial , con los recíprocos de los factoriales para sus coeficientes, fue formulada por primera vez en 1676 por Isaac Newton en una carta a Gottfried Wilhelm Leibniz . ^[14] Otras obras importantes de las primeras matemáticas europeas sobre factoriales incluyen una amplia cobertura en un tratado de 1685 de John Wallis , un estudio de sus valores aproximados para grandes valores de por Abraham de Moivre en 1721, una carta de 1729 de James Stirling a de Moivre indicando lo que se conoció como la aproximación de Stirling , y el trabajo al mismo tiempo de Daniel Bernoulli y Leonhard Euler formulando la extensión continua de la función factorial a la función gamma . ^[15] Adrien-Marie Legendre incluyó la fórmula de Legendre , que describe los exponentes en la factorización de factoriales en potencias primos , en un texto de 1808 sobre teoría de números . ^[16]${\estilo de visualización n}$

La notación para factoriales fue introducida por el matemático francés Christian Kramp en 1808. ^[17] También se han utilizado muchas otras notaciones. Otra notación posterior , en la que el argumento del factorial estaba medio encerrado por los lados izquierdo e inferior de una caja, fue popular durante algún tiempo en Gran Bretaña y Estados Unidos, pero cayó en desuso, tal vez porque es difícil de componer. ^[17] La ​​palabra "factorial" (originalmente en francés: factorielle ) fue utilizada por primera vez en 1800 por Louis François Antoine Arbogast , ^[18] en el primer trabajo sobre la fórmula de Faà di Bruno , ^[19] pero refiriéndose a un concepto más general de productos de progresiones aritméticas . Los "factores" a los que se refiere este nombre son los términos de la fórmula del producto para el factorial. ^[20]${\estilo de visualización n!}$${\displaystyle \vert \!{\underline {\,n}}}$

La función factorial de un entero positivo se define como el producto de todos los enteros positivos no mayores que ^[1]. Esto se puede escribir de manera más concisa en notación de producto como ^[1].${\estilo de visualización n}$${\estilo de visualización n}$$${\displaystyle n!=1\cdot 2\cdot 3\cdots (n-2)\cdot (n-1)\cdot n.}$$$${\displaystyle n!=\prod _{i=1}^{n}i.}$$

Si se cambia esta fórmula del producto para conservar todos los términos excepto el último, se definiría un producto de la misma forma, para un factorial más pequeño. Esto conduce a una relación de recurrencia , según la cual cada valor de la función factorial se puede obtener multiplicando el valor anterior por : ^[21]${\estilo de visualización n}$ Por ejemplo, .$${\displaystyle n!=n\cdot (n-1)!.}$$${\displaystyle 5!=5\cdot 4!=5\cdot 24=120}$

El factorial de ${\estilo de visualización 0}$ es ,${\estilo de visualización 1}$ o en símbolos, . Hay varias motivaciones para esta definición:${\estilo de visualización 0!=1}$

• Para , la definición de como producto no implica el producto de ningún número, y por lo tanto es un ejemplo de la convención más amplia de que el producto vacío , un producto de ningún factor, es igual a la identidad multiplicativa. ^[22]${\estilo de visualización n=0}$${\estilo de visualización n!}$
• Hay exactamente una permutación de cero objetos: al no haber nada que permutar, el único reordenamiento es no hacer nada. ^[21]
• Esta convención hace que muchas identidades en combinatoria sean válidas para todas las elecciones válidas de sus parámetros. Por ejemplo, la cantidad de maneras de elegir todos los elementos de un conjunto de es una identidad de coeficiente binomial que solo sería válida con . ^[23]${\estilo de visualización n}$${\estilo de visualización n}$${\textstyle {\tbinom {n}{n}}={\tfrac {n!}{n!0!}}=1,}$${\estilo de visualización 0!=1}$
• Con , la relación de recurrencia para el factorial sigue siendo válida en . Por lo tanto, con esta convención, un cálculo recursivo del factorial necesita tener solo el valor de cero como caso base , simplificando el cálculo y evitando la necesidad de casos especiales adicionales. ^[24]${\estilo de visualización 0!=1}$${\estilo de visualización n=1}$
• La configuración permite la expresión compacta de muchas fórmulas, como la función exponencial , como una serie de potencias : ^[14]${\estilo de visualización 0!=1}$${\textstyle e^{x}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}.}$
• Esta elección coincide con la función gamma , y ​​la función gamma debe tener este valor para ser una función continua . ^[25]${\displaystyle 0!=\Gamma (0+1)=1}$

Los primeros usos de la función factorial implican contar permutaciones : hay diferentes formas de organizar objetos distintos en una secuencia. ^[26] Los factoriales aparecen de forma más amplia en muchas fórmulas en combinatoria , para dar cuenta de diferentes ordenaciones de objetos. Por ejemplo, los coeficientes binomiales cuentan las combinaciones de elementos (subconjuntos de elementos) de un conjunto con elementos, y se pueden calcular a partir de factoriales utilizando la fórmula ^[27] Los números de Stirling del primer tipo suman los factoriales y cuentan las permutaciones de agrupadas en subconjuntos con el mismo número de ciclos. ^[28] Otra aplicación combinatoria es en el conteo de desarreglos , permutaciones que no dejan ningún elemento en su posición original; el número de desarreglos de elementos es el entero más cercano a . ^[29]${\estilo de visualización n!}$${\estilo de visualización n}$ ${\displaystyle {\tbinom {n}{k}}}$${\estilo de visualización k}$ ${\estilo de visualización k}$${\estilo de visualización n}$ $${\displaystyle {\binom {n}{k}}={\frac {n!}{k!(nk)!}}.}$$${\estilo de visualización n}$${\estilo de visualización n}$ ${\displaystyle n!/e}$

En álgebra , los factoriales surgen a través del teorema del binomio , que utiliza coeficientes binomiales para expandir potencias de sumas. ^[30] También aparecen en los coeficientes utilizados para relacionar ciertas familias de polinomios entre sí, por ejemplo en las identidades de Newton para polinomios simétricos . ^[31] Su uso para contar permutaciones también se puede reformular algebraicamente: los factoriales son los órdenes de grupos simétricos finitos . ^[32] En cálculo , los factoriales aparecen en la fórmula de Faà di Bruno para encadenar derivadas superiores. ^[19] En análisis matemático , los factoriales aparecen frecuentemente en los denominadores de series de potencias , más notablemente en la serie para la función exponencial , ^[14] y en los coeficientes de otras series de Taylor (en particular las de las funciones trigonométricas e hiperbólicas ), donde cancelan factores de que vienen de la derivada ésima de . ^[33] Este uso de factoriales en series de potencias se conecta con la combinatoria analítica a través de la función generadora exponencial , que para una clase combinatoria con elementos de tamaño se define como la serie de potencias ^[34]$${\displaystyle e^{x}=1+{\frac {x}{1}}+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+\cdots =\sum _{i=0}^{\infty }{\frac {x^{i}}{i!}},}$$${\estilo de visualización n!}$${\estilo de visualización n}$ $Estilo de visualización x^{n}}$${\displaystyle n_{i}}$${\estilo de visualización i}$ $${\displaystyle \sum_{i=0}^{\infty} {\frac {x^{i}n_{i}}{i!}}.}$$

En teoría de números , la propiedad más destacada de los factoriales es la divisibilidad de por todos los números enteros positivos hasta , descrita con mayor precisión para los factores primos por la fórmula de Legendre . De ello se deduce que se pueden encontrar números primos arbitrariamente grandes como factores primos de los números , lo que conduce a una prueba del teorema de Euclides de que el número de primos es infinito. ^[35] Cuando es primo en sí mismo se llama primo factorial ; ^[36] en relación con esto, el problema de Brocard , también planteado por Srinivasa Ramanujan , se refiere a la existencia de números cuadrados de la forma . ^[37] Por el contrario, todos los números deben ser compuestos, lo que demuestra la existencia de huecos primos arbitrariamente grandes . ^[38] Una prueba elemental del postulado de Bertrand sobre la existencia de un primo en cualquier intervalo de la forma , uno de los primeros resultados de Paul Erdős , se basó en las propiedades de divisibilidad de los factoriales. ^{[39] [40]} El sistema de numeración factorial es una notación de base mixta para números en la que los valores de posición de cada dígito son factoriales. ^[41]${\estilo de visualización n!}$${\estilo de visualización n}$${\displaystyle n!\pm 1}$${\displaystyle n!\pm 1}$${\estilo de visualización n!+1}$${\displaystyle n!+2,n!+3,\puntos n!+n}$${\estilo de visualización [n,2n]}$

Los factoriales se utilizan ampliamente en la teoría de la probabilidad , por ejemplo en la distribución de Poisson ^[42] y en las probabilidades de permutaciones aleatorias . ^[43] En informática , además de aparecer en el análisis de búsquedas de fuerza bruta sobre permutaciones, ^[44] los factoriales surgen en el límite inferior del número de comparaciones necesarias para ordenar por comparación un conjunto de elementos, ^{[45] y en el análisis de} tablas hash encadenadas , donde la distribución de claves por celda se puede aproximar con precisión mediante una distribución de Poisson. ^[46] Además, los factoriales aparecen naturalmente en fórmulas de física cuántica y estadística , donde a menudo se consideran todas las permutaciones posibles de un conjunto de partículas. En mecánica estadística , los cálculos de entropía como la fórmula de entropía de Boltzmann o la ecuación de Sackur-Tetrode deben corregir el recuento de microestados dividiéndolos por los factoriales de los números de cada tipo de partícula indistinguible para evitar la paradoja de Gibbs . La física cuántica proporciona la razón subyacente por la que estas correcciones son necesarias. ^[47]${\displaystyle \log _{2}n!=n\log _{2}nO(n)}$${\estilo de visualización n}$

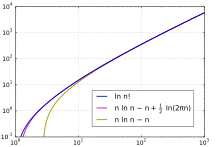
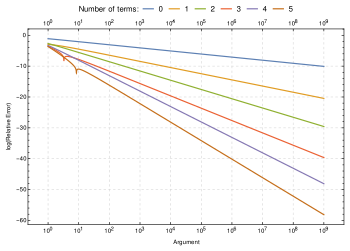
Como función de ,${\estilo de visualización n}$ el factorial tiene un crecimiento más rápido que el exponencial , pero crece más lentamente que una función exponencial doble . ^[48] Su tasa de crecimiento es similar a ,${\estilo de visualización n^{n}}$ pero más lenta por un factor exponencial. Una forma de aproximarse a este resultado es tomando el logaritmo natural del factorial, que convierte su fórmula de producto en una suma, y ​​luego estimar la suma por una integral: Exponenciando el resultado (e ignorando el término despreciable) se aproxima como . ^[49] Acotando más cuidadosamente la suma tanto por encima como por debajo por una integral, usando la regla del trapezoide , se muestra que esta estimación necesita un factor de corrección proporcional a . La constante de proporcionalidad para esta corrección se puede encontrar a partir del producto de Wallis , que se expresa como una razón límite de factoriales y potencias de dos. El resultado de estas correcciones es la aproximación de Stirling : ^[50] Aquí, el símbolo significa que, como tiende a infinito, la razón entre los lados izquierdo y derecho se acerca a uno en el límite . La fórmula de Stirling proporciona el primer término en una serie asintótica que se vuelve aún más precisa cuando se lleva a un mayor número de términos: ^[51] Una versión alternativa utiliza solo exponentes impares en los términos de corrección: ^[51] Srinivasa Ramanujan , Bill Gosper y otros también han desarrollado muchas otras variaciones de estas fórmulas . ^[51]$${\displaystyle \ln n!=\sum _{x=1}^{n}\ln x\approx \int _{1}^{n}\ln x\,dx=n\ln n-n+1.}$$${\estilo de visualización +1}$${\estilo de visualización n!}$${\displaystyle (n/e)^{n}}$${\displaystyle {\sqrt {n}}}$${\estilo de visualización \pi}$$${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\,.}$$${\estilo de visualización \sim}$${\estilo de visualización n}$$${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots \right).}$$$${\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp \left({\frac {1}{12n}}-{\frac {1}{360n^{3}}}+{\frac {1}{1260n^{5}}}-{\frac {1}{1680n^{7}}}+\cdots \right).}$$

El logaritmo binario del factorial, utilizado para analizar la clasificación por comparación , se puede estimar con mucha precisión utilizando la aproximación de Stirling. En la fórmula siguiente, el término invoca la notación O mayúscula . ^[45]${\estilo de visualización O(1)}$$${\displaystyle \log _{2}n!=n\log _{2}n-(\log _{2}e)n+{\frac {1}{2}}\log _{2}n+O(1).}$$

La fórmula del producto para el factorial implica que es divisible por todos los números primos que son como máximo , y por ningún número primo mayor. ^[52] Información más precisa sobre su divisibilidad se da por la fórmula de Legendre , que da el exponente de cada primo en la factorización prima de como ^{[53] [54]} Aquí denota la suma de los dígitos base de , y el exponente dado por esta fórmula también se puede interpretar en matemáticas avanzadas como la valoración p -ádica del factorial. ^[54] La aplicación de la fórmula de Legendre a la fórmula del producto para coeficientes binomiales produce el teorema de Kummer , un resultado similar sobre el exponente de cada primo en la factorización de un coeficiente binomial. ^[55] Agrupar los factores primos del factorial en potencias primos de diferentes maneras produce las particiones multiplicativas de factoriales . ^[56]${\displaystyle n!}$${\displaystyle n}$${\displaystyle p}$${\displaystyle n!}$$${\displaystyle \sum _{i=1}^{\infty }\left\lfloor {\frac {n}{p^{i}}}\right\rfloor ={\frac {n-s_{p}(n)}{p-1}}.}$$${\displaystyle s_{p}(n)}$${\displaystyle p}$${\displaystyle n}$

El caso especial de la fórmula de Legendre para da el número de ceros finales en la representación decimal de los factoriales. ^[57] Según esta fórmula, el número de ceros se puede obtener restando los dígitos de base 5 de de , y dividiendo el resultado por cuatro. ^[58] La fórmula de Legendre implica que el exponente del primo es siempre mayor que el exponente de , por lo que cada factor de cinco se puede emparejar con un factor de dos para producir uno de estos ceros finales. ^[57] Los dígitos iniciales de los factoriales se distribuyen de acuerdo con la ley de Benford . ^[59] Cada secuencia de dígitos, en cualquier base, es la secuencia de dígitos iniciales de algún número factorial en esa base. ^[60]${\displaystyle p=5}$${\displaystyle n}$${\displaystyle n}$${\displaystyle p=2}$${\displaystyle p=5}$

Otro resultado sobre la divisibilidad de factoriales, el teorema de Wilson , establece que es divisible por si y solo si es un número primo . ^[52] Para cualquier entero dado , la función de Kempner de está dada por el menor para el cual divide a . ^[61] Para casi todos los números (todos excepto un subconjunto de excepciones con densidad asintótica cero), coincide con el mayor factor primo de . ^[62]${\displaystyle (n-1)!+1}$${\displaystyle n}$${\displaystyle n}$${\displaystyle x}$${\displaystyle x}$${\displaystyle n}$${\displaystyle x}$${\displaystyle n!}$${\displaystyle x}$

El producto de dos factoriales, , siempre divide exactamente a . ^[63] Hay infinitos factoriales que son iguales al producto de otros factoriales: si es en sí mismo cualquier producto de factoriales, entonces es igual a ese mismo producto multiplicado por un factorial más, . Los únicos ejemplos conocidos de factoriales que son productos de otros factoriales pero que no son de esta forma "trivial" son , , y . ^[64] Se seguiría de la conjetura abc que solo hay un número finito de ejemplos no triviales. ^[65]${\displaystyle m!\cdot n!}$${\displaystyle (m+n)!}$${\displaystyle n}$${\displaystyle n!}$${\displaystyle (n-1)!}$${\displaystyle 9!=7!\cdot 3!\cdot 3!\cdot 2!}$ ${\displaystyle 10!=7!\cdot 6!=7!\cdot 5!\cdot 3!}$${\displaystyle 16!=14!\cdot 5!\cdot 2!}$

El máximo común divisor de los valores de un polinomio primitivo de grado sobre los números enteros divide exactamente a . ^[63]${\displaystyle d}$${\displaystyle d!}$

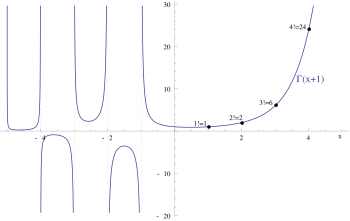
Hay infinitas formas de extender los factoriales a una función continua . ^[66] La más utilizada de ellas ^[67] utiliza la función gamma , que puede definirse para números reales positivos como la integral La función resultante está relacionada con el factorial de un entero no negativo mediante la ecuación que puede usarse como definición del factorial para argumentos no enteros. En todos los valores para los que se definen tanto y , la función gamma obedece a la ecuación funcional que generaliza la relación de recurrencia para los factoriales. ^[66]$${\displaystyle \Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\,dx.}$$${\displaystyle n}$$${\displaystyle n!=\Gamma (n+1),}$$${\displaystyle x}$${\displaystyle \Gamma (x)}$${\displaystyle \Gamma (x-1)}$$${\displaystyle \Gamma (n)=(n-1)\Gamma (n-1),}$$

La misma integral converge de manera más general para cualquier número complejo cuya parte real sea positiva. Puede extenderse a los puntos no enteros en el resto del plano complejo resolviendo la fórmula de reflexión de Euler . Sin embargo, esta fórmula no puede usarse en números enteros porque, para ellos, el término produciría una división por cero . El resultado de este proceso de extensión es una función analítica , la continuación analítica de la fórmula integral para la función gamma. Tiene un valor distinto de cero en todos los números complejos, excepto para los enteros no positivos donde tiene polos simples . En consecuencia, esto proporciona una definición para el factorial en todos los números complejos que no sean los enteros negativos. ^[67] Una propiedad de la función gamma, que la distingue de otras interpolaciones continuas de los factoriales, está dada por el teorema de Bohr-Mollerup , que establece que la función gamma (desplazada por uno) es la única función log-convexa en los números reales positivos que interpola los factoriales y obedece a la misma ecuación funcional. Un teorema de unicidad relacionado de Helmut Wielandt establece que la función gamma compleja y sus múltiplos escalares son las únicas funciones holomorfas en el semiplano complejo positivo que obedecen a la ecuación funcional y permanecen acotadas para números complejos con parte real entre 1 y 2. ^[68]${\displaystyle z}$$${\displaystyle \Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin \pi z}}.}$$${\displaystyle \sin \pi z}$

Otras funciones complejas que interpolan los valores factoriales incluyen la función gamma de Hadamard , que es una función completa sobre todos los números complejos, incluidos los enteros no positivos. ^{[69] [70]} En los números p -ádicos , no es posible interpolar continuamente la función factorial directamente, porque los factoriales de los enteros grandes (un subconjunto denso de los p -ádicos) convergen a cero de acuerdo con la fórmula de Legendre, lo que obliga a que cualquier función continua que esté cerca de sus valores sea cero en todas partes. En cambio, la función gamma p -ádica proporciona una interpolación continua de una forma modificada del factorial, omitiendo los factores en el factorial que son divisibles por p . ^[71]

La función digamma es la derivada logarítmica de la función gamma. Así como la función gamma proporciona una interpolación continua de los factoriales, compensada por uno, la función digamma proporciona una interpolación continua de los números armónicos , compensada por la constante de Euler-Mascheroni . ^[72]

La función factorial es una característica común en las calculadoras científicas . ^[73] También se incluye en bibliotecas de programación científica como el módulo de funciones matemáticas de Python ^[74] y la biblioteca Boost C++ . ^[75] Si la eficiencia no es una preocupación, calcular factoriales es trivial: simplemente multiplica sucesivamente una variable inicializada a${\displaystyle 1}$ por los números enteros hasta .${\displaystyle n}$ La simplicidad de este cálculo lo convierte en un ejemplo común en el uso de diferentes estilos y métodos de programación informática. ^[76]

El cálculo de se puede expresar en pseudocódigo usando iteración ^[77] como${\displaystyle n!}$

definir factorial( n ): f  := 1 para i  := 1, 2, 3, ..., n : f  := f * i devuelve f

o utilizando la recursión ^[78] basándose en su relación de recurrencia como

definir factorial( n ): si ( n = 0) devuelve 1 devuelve n * factorial( n − 1)

Otros métodos adecuados para su cálculo incluyen la memorización , ^[79] la programación dinámica , ^[80] y la programación funcional . ^[81] La complejidad computacional de estos algoritmos puede analizarse utilizando el modelo de cálculo de máquina de acceso aleatorio de costo unitario , en el que cada operación aritmética toma un tiempo constante y cada número utiliza una cantidad constante de espacio de almacenamiento. En este modelo, estos métodos pueden calcular en tiempo , y la versión iterativa utiliza espacio . A menos que se optimice para la recursión de cola , la versión recursiva toma espacio lineal para almacenar su pila de llamadas . ^[82] Sin embargo, este modelo de cálculo solo es adecuado cuando es lo suficientemente pequeño como para permitir que quepa en una palabra de máquina . ^[83] Los valores 12! y 20! son los factoriales más grandes que se pueden almacenar en, respectivamente, los enteros de 32 bits ^[84] y 64 bits . ^[85] El punto flotante puede representar factoriales más grandes, pero aproximadamente en lugar de exactamente, y aún se desbordará para factoriales mayores que . ^[84]${\displaystyle n!}$${\displaystyle O(n)}$${\displaystyle O(1)}$${\displaystyle n}$${\displaystyle n!}$ ${\displaystyle 170!}$

El cálculo exacto de factoriales más grandes implica aritmética de precisión arbitraria , debido al rápido crecimiento y al desbordamiento de enteros . El tiempo de cálculo se puede analizar como una función del número de dígitos o bits en el resultado. ^[85] Por la fórmula de Stirling, tiene bits. ^[86] El algoritmo de Schönhage-Strassen puede producir un producto de -bit en tiempo , y se conocen algoritmos de multiplicación más rápidos que toman tiempo . ^[87] Sin embargo, calcular el factorial involucra productos repetidos, en lugar de una sola multiplicación, por lo que estos límites de tiempo no se aplican directamente. En este contexto, calcular multiplicando los números del 1 al en secuencia es ineficiente, porque involucra multiplicaciones, una fracción constante de las cuales toman tiempo cada una, dando un tiempo total . Un mejor enfoque es realizar las multiplicaciones como un algoritmo de divide y vencerás que multiplica una secuencia de números dividiéndola en dos subsecuencias de números, multiplica cada subsecuencia y combina los resultados con una última multiplicación. Este enfoque del factorial requiere un tiempo total : un logaritmo proviene del número de bits del factorial, un segundo proviene del algoritmo de multiplicación y un tercero proviene del algoritmo de divide y vencerás. ^[88]${\displaystyle n!}$${\displaystyle b=O(n\log n)}$${\displaystyle b}$${\displaystyle O(b\log b\log \log b)}$${\displaystyle O(b\log b)}$${\displaystyle n!}$${\displaystyle n}$${\displaystyle n}$${\displaystyle O(n\log ^{2}n)}$${\displaystyle O(n^{2}\log ^{2}n)}$${\displaystyle i}$${\displaystyle i/2}$${\displaystyle O(n\log ^{3}n)}$

Se obtiene una eficiencia aún mejor calculando n ! a partir de su factorización prima, basándose en el principio de que la exponenciación por cuadrado es más rápida que expandir un exponente en un producto. ^{[86] [89]} Un algoritmo para esto por Arnold Schönhage comienza encontrando la lista de los primos hasta , por${\displaystyle n}$ ejemplo usando la criba de Eratóstenes , y usa la fórmula de Legendre para calcular el exponente para cada primo. Luego calcula el producto de las potencias de los primos con estos exponentes, usando un algoritmo recursivo, de la siguiente manera:

• Utilice dividir y vencer para calcular el producto de los números primos cuyos exponentes son impares.
• Divida todos los exponentes por dos (redondeando hacia abajo a un número entero), calcule recursivamente el producto de las potencias primas con estos exponentes más pequeños y eleve al cuadrado el resultado.
• Multiplica juntos los resultados de los dos pasos anteriores.

El producto de todos los primos hasta es un número de -bits, según el teorema de los números primos , por lo que el tiempo para el primer paso es , con un logaritmo proveniente del algoritmo divide y vencerás y otro proveniente del algoritmo de multiplicación. En las llamadas recursivas al algoritmo, se puede invocar nuevamente el teorema de los números primos para demostrar que los números de bits en los productos correspondientes disminuyen en un factor constante en cada nivel de recursión, por lo que el tiempo total para estos pasos en todos los niveles de recursión se suma en una serie geométrica a . El tiempo para elevar al cuadrado en el segundo paso y la multiplicación en el tercer paso son nuevamente , porque cada uno es una sola multiplicación de un número con bits. Nuevamente, en cada nivel de recursión los números involucrados tienen una fracción constante de bits (porque de lo contrario elevarlos al cuadrado repetidamente produciría un resultado final demasiado grande) por lo que nuevamente las cantidades de tiempo para estos pasos en las llamadas recursivas se suman en una serie geométrica a . Consecuentemente, todo el algoritmo toma tiempo , proporcional a una sola multiplicación con el mismo número de bits en su resultado. ^[89]${\displaystyle n}$${\displaystyle O(n)}$${\displaystyle O(n\log ^{2}n)}$ ${\displaystyle O(n\log ^{2}n)}$${\displaystyle O(n\log ^{2}n)}$${\displaystyle O(n\log n)}$${\displaystyle O(n\log ^{2}n)}$${\displaystyle O(n\log ^{2}n)}$

Varias otras secuencias de números enteros son similares o están relacionadas con los factoriales:

Factorial alterno

El factorial alterno es el valor absoluto de la suma alternada de los primeros factoriales, . Estos se han estudiado principalmente en relación con su primalidad; solo un número finito de ellos puede ser primo, pero no se conoce una lista completa de primos de esta forma. ^[90]${\displaystyle n}$${\textstyle \sum _{i=1}^{n}(-1)^{n-i}i!}$

Factorial de Bhargava

Los factoriales de Bhargava son una familia de secuencias de números enteros definidas por Manjul Bhargava con propiedades teóricas de números similares a los factoriales, incluyendo los factoriales mismos como un caso especial. ^[63]

Factor doble

El producto de todos los números enteros impares hasta algún número entero${\displaystyle n}$ positivo impar se llama factorial doble de ,${\displaystyle n}$ y se denota por . ^[91] Es decir, por ejemplo, 9!! = 1 × 3 × 5 × 7 × 9 = 945 . Los factoriales dobles se utilizan en integrales trigonométricas , ^[92] en expresiones para la función gamma en semienteros y los volúmenes de hiperesferas , ^[93] y en el conteo de árboles binarios y emparejamientos perfectos . ^{[91] [94]}${\displaystyle n!!}$$${\displaystyle (2k-1)!!=\prod _{i=1}^{k}(2i-1)={\frac {(2k)!}{2^{k}k!}}.}$$

Factorial exponencial

Así como los números triangulares suman los números de a , y los factoriales toman su producto, el factorial exponencial potencia. El factorial exponencial se define recursivamente como . Por ejemplo, el factorial exponencial de 4 es Estos números crecen mucho más rápido que los factoriales regulares. ^[95]${\displaystyle 1}$ ${\displaystyle n}$${\displaystyle a_{0}=1,\ a_{n}=n^{a_{n-1}}}$$${\displaystyle 4^{3^{2^{1}}}=262144.}$$

Factorial descendente

Las notaciones o se utilizan a veces para representar el producto de los números enteros contando hasta e incluyendo , igual a . Esto también se conoce como factorial descendente o factorial inverso, y la notación es un símbolo de Pochhammer. ^[96] Los factoriales descendentes cuentan el número de secuencias diferentes de elementos distintos que se pueden extraer de un universo de elementos. ^[97] Se presentan como coeficientes en las derivadas superiores de polinomios, ^[98] y en los momentos factoriales de variables aleatorias . ^[99]${\displaystyle (x)_{n}}$${\displaystyle x^{\underline {n}}}$${\displaystyle n}$${\displaystyle x}$${\displaystyle x!/(x-n)!}$${\displaystyle (x)_{n}}$${\displaystyle n}$${\displaystyle x}$

Hiperfactoriales

El hiperfactorial de es el producto de . Estos números forman los discriminantes de los polinomios de Hermite . ^[100] Pueden interpolarse continuamente mediante la función K , ^[101] y obedecen a analogías con la fórmula de Stirling ^[102] y el teorema de Wilson. ^[103]${\displaystyle n}$${\displaystyle 1^{1}\cdot 2^{2}\cdots n^{n}}$

Números de Jordan–Pólya

Los números de Jordan-Pólya son productos de factores, lo que permite repeticiones. Cada árbol tiene un grupo de simetría cuyo número de simetrías es un número de Jordan-Pólya, y cada número de Jordan-Pólya cuenta las simetrías de algún árbol. ^[104]

Primordial

El primorial es el producto de números primos menores o iguales a ; esta construcción les da algunas propiedades de divisibilidad similares a los factoriales, ^[36] pero a diferencia de los factoriales no tienen cuadrados . ^[105] Al igual que con los primos factoriales , los investigadores han estudiado los primos primoriales . ^[36]${\displaystyle n\#}$${\displaystyle n}$ ${\displaystyle n!\pm 1}$ ${\displaystyle n\#\pm 1}$

Subfactorial

El subfactorial da como resultado el número de desajustes de un conjunto de objetos. A veces se denota como , y es igual al entero más cercano a . ^[29]${\displaystyle n}$${\displaystyle !n}$${\displaystyle n!/e}$

Superfactorial

El superfactorial de es el producto de los primeros factoriales. Los superfactoriales se interpolan continuamente mediante la función G de Barnes . ^[106]${\displaystyle n}$${\displaystyle n}$

Wikimedia Commons tiene medios relacionados con Factorial (función) .

• Secuencia OEIS A000142 (Números factoriales)
• "Factorial". Enciclopedia de Matemáticas . EMS Press . 2001 [1994].
• Weisstein, Eric W. "Factorial". MathWorld .