Variable aleatoria

Parte de una serie sobre estadísticas
Teoría de la probabilidad
Probabilidad Axiomas Determinismo Sistema Indeterminismo Aleatoriedad
Espacio de probabilidad Espacio muestral Evento Eventos colectivamente exhaustivos Evento elemental Exclusividad mutua Resultado Semifallo Experimento El proceso de Bernoulli Distribución de probabilidad Distribución de Bernoulli Distribución binomial Distribución exponencial Distribución normal Distribución de Pareto Distribución de Poisson Medida de probabilidad Variable aleatoria Proceso de Bernoulli Continuo o discreto Valor esperado Diferencia Cadena de Markov Valor observado Paseo aleatorio Proceso estocástico
Evento complementario Probabilidad conjunta Probabilidad marginal Probabilidad condicional
Independencia Independencia condicional Ley de probabilidad total Ley de los grandes números Teorema de Bayes Desigualdad de Boole
Diagrama de Venn Diagrama de árbol
en a mi

Una variable aleatoria (también llamada cantidad aleatoria , variable aleatoria o variable estocástica ) es una formalización matemática de una cantidad u objeto que depende de eventos aleatorios . ^[1] El término "variable aleatoria" en su definición matemática no se refiere ni a la aleatoriedad ni a la variabilidad ^[2] , sino a una función matemática en la que

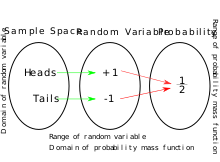
• el dominio es el conjunto de resultados posibles en un espacio muestral (por ejemplo, el conjunto que son los posibles lados superiores de una moneda lanzada, cara o cruz como resultado de lanzar una moneda); y${\estilo de visualización \{H,T\}}$${\estilo de visualización H}$${\estilo de visualización T}$
• el rango es un espacio medible (por ejemplo, correspondiente al dominio anterior, el rango podría ser el conjunto si, por ejemplo, caras se asignan a -1 y se asignan a 1). Por lo general, el rango de una variable aleatoria es un subconjunto de los números reales .${\estilo de visualización \{-1,1\}}$${\estilo de visualización H}$${\estilo de visualización T}$

De manera informal, la aleatoriedad suele representar algún elemento fundamental del azar, como en el lanzamiento de un dado ; también puede representar incertidumbre, como un error de medición . ^[1] Sin embargo, la interpretación de la probabilidad es filosóficamente complicada, e incluso en casos específicos no siempre es sencilla. El análisis puramente matemático de variables aleatorias es independiente de tales dificultades de interpretación y puede basarse en un planteamiento axiomático riguroso.

En el lenguaje matemático formal de la teoría de la medida , una variable aleatoria se define como una función medible de un espacio de medida de probabilidad (llamado espacio muestral ) a un espacio medible . Esto permite considerar la medida de empuje hacia adelante , que se llama la distribución de la variable aleatoria; la distribución es, por lo tanto, una medida de probabilidad en el conjunto de todos los valores posibles de la variable aleatoria. Es posible que dos variables aleatorias tengan distribuciones idénticas pero difieran de manera significativa; por ejemplo, pueden ser independientes .

Es común considerar los casos especiales de variables aleatorias discretas y variables aleatorias absolutamente continuas , que corresponden a si una variable aleatoria se valora en un subconjunto contable o en un intervalo de números reales . Existen otras posibilidades importantes, especialmente en la teoría de procesos estocásticos , en las que es natural considerar secuencias aleatorias o funciones aleatorias . A veces se considera que una variable aleatoria se valora automáticamente en los números reales, y las cantidades aleatorias más generales se denominan en cambio elementos aleatorios .

Según George Mackey , Pafnuty Chebyshev fue la primera persona "en pensar sistemáticamente en términos de variables aleatorias". ^[3]

Una variable aleatoria es una función medible de un espacio muestral como un conjunto de resultados posibles a un espacio medible . La definición axiomática técnica requiere que el espacio muestral sea un espacio muestral de un triple de probabilidad (véase la definición de teoría de la medida). Una variable aleatoria se denota a menudo con letras romanas mayúsculas como . ^[4]${\estilo de visualización X}$ ${\displaystyle X\colon \Omega \to E}$${\estilo de visualización\Omega}$ ${\estilo de visualización E}$${\estilo de visualización\Omega}$ ${\displaystyle (\Omega ,{\mathcal {F}},\operatorname {P} )}$${\estilo de visualización X, Y, Z, T}$

La probabilidad de que tome un valor en un conjunto medible se escribe como${\estilo de visualización X}$${\displaystyle S\subseteq E}$

${\displaystyle \operatorname {P} (X\in S)=\operatorname {P} (\{\omega \in \Omega \mid X(\omega )\in S\})}$.

En muchos casos, tiene un valor real , es decir , . En algunos contextos, el término elemento aleatorio (ver extensiones) se utiliza para indicar una variable aleatoria que no tiene esta forma.${\estilo de visualización X}$${\displaystyle E=\mathbb {R}}$

Cuando la imagen (o rango) de es finita o infinitamente contable , la variable aleatoria se denomina variable aleatoria discreta ^{[5] : 399} y su distribución es una distribución de probabilidad discreta , es decir, puede describirse mediante una función de masa de probabilidad que asigna una probabilidad a cada valor en la imagen de . Si la imagen es incontablemente infinita (normalmente un intervalo ), entonces se denomina variable aleatoria continua . ^{[6] [7]} En el caso especial de que sea absolutamente continua , su distribución puede describirse mediante una función de densidad de probabilidad , que asigna probabilidades a intervalos; en particular, cada punto individual debe tener necesariamente probabilidad cero para una variable aleatoria absolutamente continua. No todas las variables aleatorias continuas son absolutamente continuas. ^[8]${\estilo de visualización X}$${\estilo de visualización X}$${\estilo de visualización X}$

Cualquier variable aleatoria puede describirse mediante su función de distribución acumulativa , que describe la probabilidad de que la variable aleatoria sea menor o igual a un valor determinado.

El término "variable aleatoria" en estadística se limita tradicionalmente al caso de valores reales ( ). En este caso, la estructura de los números reales permite definir magnitudes como el valor esperado y la varianza de una variable aleatoria, su función de distribución acumulativa y los momentos de su distribución.${\displaystyle E=\mathbb {R}}$

Sin embargo, la definición anterior es válida para cualquier espacio medible de valores. Por lo tanto, se pueden considerar elementos aleatorios de otros conjuntos , como valores booleanos aleatorios , valores categóricos , números complejos , vectores , matrices , secuencias , árboles , conjuntos , formas , variedades y funciones . Se puede hacer referencia, entonces, específicamente a una variable aleatoria de tipo , o a una variable aleatoria de valor .${\estilo de visualización E}$${\estilo de visualización E}$ ${\estilo de visualización E}$${\estilo de visualización E}$

Este concepto más general de un elemento aleatorio es particularmente útil en disciplinas como la teoría de grafos , el aprendizaje automático , el procesamiento del lenguaje natural y otros campos de las matemáticas discretas y la informática , donde a menudo se está interesado en modelar la variación aleatoria de estructuras de datos no numéricas . En algunos casos, no obstante, es conveniente representar cada elemento de , utilizando uno o más números reales. En este caso, un elemento aleatorio puede representarse opcionalmente como un vector de variables aleatorias de valor real (todas definidas en el mismo espacio de probabilidad subyacente , que permite que las diferentes variables aleatorias covaríen ). Por ejemplo:${\estilo de visualización E}$${\estilo de visualización\Omega}$

• Una palabra aleatoria puede representarse como un entero aleatorio que sirve como índice en el vocabulario de palabras posibles. Alternativamente, puede representarse como un vector indicador aleatorio, cuya longitud es igual al tamaño del vocabulario, donde los únicos valores de probabilidad positiva son , , y la posición del 1 indica la palabra.${\displaystyle (1\ 0\ 0\ 0\ \cdots )}$${\displaystyle (0\ 1\ 0\ 0\ \cdots )}$${\displaystyle (0\ 0\ 1\ 0\ \cdots )}$
• Una oración aleatoria de una longitud determinada puede representarse como un vector de palabras aleatorias.${\estilo de visualización N}$${\estilo de visualización N}$
• Un gráfico aleatorio en vértices dados puede representarse como una matriz de variables aleatorias, cuyos valores especifican la matriz de adyacencia del gráfico aleatorio.${\estilo de visualización N}$${\displaystyle N\veces N}$
• Una función aleatoria puede representarse como una colección de variables aleatorias , que dan los valores de la función en los distintos puntos del dominio de la función. Las son variables aleatorias ordinarias de valor real siempre que la función sea de valor real. Por ejemplo, un proceso estocástico es una función aleatoria del tiempo, un vector aleatorio es una función aleatoria de algún conjunto de índices como , y un campo aleatorio es una función aleatoria en cualquier conjunto (normalmente tiempo, espacio o un conjunto discreto).${\estilo de visualización F}$${\displaystyle F(x)}$${\displaystyle x}$${\displaystyle F(x)}$${\displaystyle 1,2,\ldots ,n}$

Si se da una variable aleatoria definida en el espacio de probabilidad , podemos hacer preguntas como "¿Qué probabilidad hay de que el valor de sea igual a 2?". Esto es lo mismo que la probabilidad del evento, que a menudo se escribe como o para abreviar.${\displaystyle X\colon \Omega \to \mathbb {R} }$${\displaystyle (\Omega ,{\mathcal {F}},\operatorname {P} )}$${\displaystyle X}$${\displaystyle \{\omega :X(\omega )=2\}\,\!}$${\displaystyle P(X=2)\,\!}$${\displaystyle p_{X}(2)}$

Al registrar todas estas probabilidades de salidas de una variable aleatoria se obtiene la distribución de probabilidad de . La distribución de probabilidad "olvida" el espacio de probabilidad particular utilizado para definir y solo registra las probabilidades de varios valores de salida de . Una distribución de probabilidad de este tipo, si es de valor real, siempre puede ser capturada por su función de distribución acumulativa.${\displaystyle X}$${\displaystyle X}$${\displaystyle X}$${\displaystyle X}$${\displaystyle X}$

${\displaystyle F_{X}(x)=\operatorname {P} (X\leq x)}$

y a veces también usando una función de densidad de probabilidad , . En términos de teoría de medidas , usamos la variable aleatoria para "empujar hacia adelante" la medida en a una medida en . La medida se llama "distribución (de probabilidad) de " o "ley de ". ^[9] La densidad , la derivada de Radon-Nikodym de con respecto a alguna medida de referencia en (a menudo, esta medida de referencia es la medida de Lebesgue en el caso de variables aleatorias continuas, o la medida de conteo en el caso de variables aleatorias discretas). El espacio de probabilidad subyacente es un dispositivo técnico utilizado para garantizar la existencia de variables aleatorias, a veces para construirlas y para definir nociones como correlación y dependencia o independencia basadas en una distribución conjunta de dos o más variables aleatorias en el mismo espacio de probabilidad. En la práctica, a menudo se elimina el espacio por completo y solo se coloca una medida en que asigna la medida 1 a toda la línea real, es decir, se trabaja con distribuciones de probabilidad en lugar de variables aleatorias. Vea el artículo sobre funciones cuantiles para un desarrollo más completo.${\displaystyle f_{X}}$${\displaystyle X}$${\displaystyle P}$${\displaystyle \Omega }$${\displaystyle p_{X}}$${\displaystyle \mathbb {R} }$${\displaystyle p_{X}}$${\displaystyle X}$${\displaystyle X}$${\displaystyle f_{X}=dp_{X}/d\mu }$${\displaystyle p_{X}}$${\displaystyle \mu }$${\displaystyle \mathbb {R} }$${\displaystyle \Omega }$${\displaystyle \Omega }$${\displaystyle \mathbb {R} }$

Consideremos un experimento en el que se elige una persona al azar. Un ejemplo de variable aleatoria puede ser la altura de la persona. Matemáticamente, la variable aleatoria se interpreta como una función que asigna la altura de la persona a la persona. Asociada a la variable aleatoria hay una distribución de probabilidad que permite calcular la probabilidad de que la altura se encuentre en cualquier subconjunto de valores posibles, como la probabilidad de que la altura esté entre 180 y 190 cm, o la probabilidad de que la altura sea menor de 150 o mayor de 200 cm.

Otra variable aleatoria puede ser el número de hijos de una persona; se trata de una variable aleatoria discreta con valores enteros no negativos. Permite el cálculo de probabilidades para valores enteros individuales (la función de masa de probabilidad o FMP) o para conjuntos de valores, incluidos los conjuntos infinitos. Por ejemplo, el evento de interés puede ser "un número par de hijos". Tanto para los conjuntos de eventos finitos como para los infinitos, sus probabilidades se pueden encontrar sumando las FMP de los elementos; es decir, la probabilidad de un número par de hijos es la suma infinita .${\displaystyle \operatorname {PMF} (0)+\operatorname {PMF} (2)+\operatorname {PMF} (4)+\cdots }$

En ejemplos como estos, el espacio muestral suele suprimirse, ya que es matemáticamente difícil de describir, y los posibles valores de las variables aleatorias se tratan entonces como un espacio muestral. Pero cuando dos variables aleatorias se miden en el mismo espacio muestral de resultados, como la altura y el número de hijos que se calculan en las mismas personas aleatorias, es más fácil rastrear su relación si se reconoce que tanto la altura como el número de hijos provienen de la misma persona aleatoria, por ejemplo, de modo que se puedan plantear preguntas sobre si dichas variables aleatorias están correlacionadas o no.

Si son conjuntos contables de números reales, y , entonces es una función de distribución discreta. Aquí , para , para . Si tomamos, por ejemplo, una enumeración de todos los números racionales como , se obtiene una función discreta que no es necesariamente una función escalonada (constante por partes).${\textstyle \{a_{n}\},\{b_{n}\}}$${\textstyle b_{n}>0}$${\textstyle \sum _{n}b_{n}=1}$${\textstyle F=\sum _{n}b_{n}\delta _{a_{n}}(x)}$${\displaystyle \delta _{t}(x)=0}$${\displaystyle x<t}$${\displaystyle \delta _{t}(x)=1}$${\displaystyle x\geq t}$${\displaystyle \{a_{n}\}}$

Los posibles resultados de un lanzamiento de moneda se pueden describir mediante el espacio muestral . Podemos introducir una variable aleatoria de valor real que modele una ganancia de $1 por una apuesta exitosa a cara de la siguiente manera:${\displaystyle \Omega =\{{\text{heads}},{\text{tails}}\}}$${\displaystyle Y}$$${\displaystyle Y(\omega )={\begin{cases}1,&{\text{if }}\omega ={\text{heads}},\\[6pt]0,&{\text{if }}\omega ={\text{tails}}.\end{cases}}}$$

Si la moneda es una moneda justa , Y tiene una función de masa de probabilidad dada por:${\displaystyle f_{Y}}$$${\displaystyle f_{Y}(y)={\begin{cases}{\tfrac {1}{2}},&{\text{if }}y=1,\\[6pt]{\tfrac {1}{2}},&{\text{if }}y=0,\end{cases}}}$$

También se puede utilizar una variable aleatoria para describir el proceso de lanzamiento de dados y los posibles resultados. La representación más obvia para el caso de dos dados es tomar el conjunto de pares de números n ₁ y n ₂ de {1, 2, 3, 4, 5, 6} (que representan los números de los dos dados) como espacio muestral. El número total de números lanzados (la suma de los números de cada par) es entonces una variable aleatoria X dada por la función que asigna el par a la suma: y (si los dados son justos ) tiene una función de masa de probabilidad f _X dada por:$${\displaystyle X((n_{1},n_{2}))=n_{1}+n_{2}}$$$${\displaystyle f_{X}(S)={\frac {\min(S-1,13-S)}{36}},{\text{ for }}S\in \{2,3,4,5,6,7,8,9,10,11,12\}}$$

Formalmente, una variable aleatoria continua es una variable aleatoria cuya función de distribución acumulativa es continua en todas partes. ^[10] No hay " huecos ", que corresponderían a números que tienen una probabilidad finita de ocurrir . En cambio, las variables aleatorias continuas casi nunca toman un valor prescrito exacto c (formalmente, ) pero hay una probabilidad positiva de que su valor se encuentre en intervalos particulares que pueden ser arbitrariamente pequeños . Las variables aleatorias continuas generalmente admiten funciones de densidad de probabilidad (PDF), que caracterizan su CDF y medidas de probabilidad ; tales distribuciones también se denominan absolutamente continuas ; pero algunas distribuciones continuas son singulares , o mezclas de una parte absolutamente continua y una parte singular.${\textstyle \forall c\in \mathbb {R} :\;\Pr(X=c)=0}$

Un ejemplo de una variable aleatoria continua sería una basada en un spinner que puede elegir una dirección horizontal. Entonces, los valores tomados por la variable aleatoria son direcciones. Podríamos representar estas direcciones por Norte, Oeste, Este, Sur, Sudeste, etc. Sin embargo, es comúnmente más conveniente mapear el espacio muestral a una variable aleatoria que toma valores que son números reales. Esto se puede hacer, por ejemplo, mapeando una dirección a un rumbo en grados en el sentido de las agujas del reloj desde el Norte. La variable aleatoria entonces toma valores que son números reales del intervalo [0, 360), siendo todas las partes del rango "igualmente probables". En este caso, X = el ángulo girado. Cualquier número real tiene probabilidad cero de ser seleccionado, pero se puede asignar una probabilidad positiva a cualquier rango de valores. Por ejemplo, la probabilidad de elegir un número en [0, 180] es 1 ⁄ 2 . En lugar de hablar de una función de masa de probabilidad, decimos que la densidad de probabilidad de X es 1/360. La probabilidad de un subconjunto de [0, 360) se puede calcular multiplicando la medida del conjunto por 1/360. En general, la probabilidad de un conjunto para una variable aleatoria continua dada se puede calcular integrando la densidad sobre el conjunto dado.

De manera más formal, dado cualquier intervalo , una variable aleatoria se denomina " variable aleatoria uniforme continua " (CURV) si la probabilidad de que tome un valor en un subintervalo depende únicamente de la longitud del subintervalo. Esto implica que la probabilidad de caer en cualquier subintervalo es proporcional a la longitud del subintervalo, es decir, si a ≤ c ≤ d ≤ b , se tiene${\textstyle I=[a,b]=\{x\in \mathbb {R} :a\leq x\leq b\}}$${\displaystyle X_{I}\sim \operatorname {U} (I)=\operatorname {U} [a,b]}$${\displaystyle X_{I}}$${\displaystyle [c,d]\subseteq [a,b]}$

$${\displaystyle \Pr \left(X_{I}\in [c,d]\right)={\frac {d-c}{b-a}}}$$

donde la última igualdad resulta del axioma de unitaridad de probabilidad. La función de densidad de probabilidad de una CURV está dada por la función indicadora de su intervalo de soporte normalizado por la longitud del intervalo: De particular interés es la distribución uniforme en el intervalo unitario . Se pueden generar muestras de cualquier distribución de probabilidad deseada calculando la función cuantil de en un número generado aleatoriamente distribuido uniformemente en el intervalo unitario. Esto explota las propiedades de las funciones de distribución acumulativa , que son un marco unificador para todas las variables aleatorias.${\displaystyle X\sim \operatorname {U} [a,b]}$$${\displaystyle f_{X}(x)={\begin{cases}\displaystyle {1 \over b-a},&a\leq x\leq b\\0,&{\text{otherwise}}.\end{cases}}}$$ ${\displaystyle [0,1]}$ ${\displaystyle \operatorname {D} }$${\displaystyle \operatorname {D} }$

Una variable aleatoria mixta es una variable aleatoria cuya función de distribución acumulativa no es ni discreta ni continua en todas partes . ^[10] Puede realizarse como una mezcla de una variable aleatoria discreta y una variable aleatoria continua; en cuyo caso la CDF será el promedio ponderado de las CDF de las variables componentes. ^[10]

Un ejemplo de una variable aleatoria de tipo mixto se basaría en un experimento en el que se lanza una moneda y se hace girar la ruleta solo si el resultado del lanzamiento de la moneda es cara. Si el resultado es cruz, X = −1; en caso contrario, X = el valor de la ruleta, como en el ejemplo anterior. Existe una probabilidad de 1 ⁄ 2 de que esta variable aleatoria tenga el valor −1. Otros rangos de valores tendrían la mitad de las probabilidades del último ejemplo.

En términos generales, cada distribución de probabilidad en la línea real es una mezcla de una parte discreta, una parte singular y una parte absolutamente continua; véase el teorema de descomposición de Lebesgue § Refinamiento . La parte discreta se concentra en un conjunto numerable, pero este conjunto puede ser denso (como el conjunto de todos los números racionales).

La definición axiomática más formal de una variable aleatoria implica la teoría de la medida . Las variables aleatorias continuas se definen en términos de conjuntos de números, junto con funciones que asignan dichos conjuntos a probabilidades. Debido a varias dificultades (por ejemplo, la paradoja de Banach-Tarski ) que surgen si dichos conjuntos no están suficientemente restringidos, es necesario introducir lo que se denomina un álgebra sigma para restringir los conjuntos posibles sobre los que se pueden definir probabilidades. Normalmente, se utiliza un álgebra sigma particular, el σ-álgebra de Borel , que permite definir probabilidades sobre cualquier conjunto que pueda derivarse directamente de intervalos continuos de números o mediante un número finito o infinito contable de uniones y/o intersecciones de dichos intervalos. ^[11]

La definición teórica de la medida es la siguiente.

Sea un espacio de probabilidad y un espacio medible . Entonces, una variable aleatoria con valor - es una función medible , lo que significa que, para cada subconjunto , su preimagen es -medible; , donde . ^[12] Esta definición nos permite medir cualquier subconjunto en el espacio objetivo observando su preimagen, que por supuesto es medible.${\displaystyle (\Omega ,{\mathcal {F}},P)}$${\displaystyle (E,{\mathcal {E}})}$${\displaystyle (E,{\mathcal {E}})}$${\displaystyle X\colon \Omega \to E}$${\displaystyle B\in {\mathcal {E}}}$${\displaystyle {\mathcal {F}}}$${\displaystyle X^{-1}(B)\in {\mathcal {F}}}$${\displaystyle X^{-1}(B)=\{\omega :X(\omega )\in B\}}$${\displaystyle B\in {\mathcal {E}}}$

En términos más intuitivos, un miembro de es un resultado posible, un miembro de es un subconjunto medible de resultados posibles, la función da la probabilidad de cada uno de esos subconjuntos mesurables, representa el conjunto de valores que la variable aleatoria puede tomar (como el conjunto de números reales), y un miembro de es un subconjunto "de buen comportamiento" (medible) de (aquellos para los que se puede determinar la probabilidad). La variable aleatoria es entonces una función de cualquier resultado a una cantidad, de modo que los resultados que conducen a cualquier subconjunto útil de cantidades para la variable aleatoria tienen una probabilidad bien definida.${\displaystyle \Omega }$${\displaystyle {\mathcal {F}}}$${\displaystyle P}$${\displaystyle E}$${\displaystyle {\mathcal {E}}}$${\displaystyle E}$

Cuando es un espacio topológico , entonces la opción más común para el σ-álgebra es el σ-álgebra de Borel , que es el σ-álgebra generado por la colección de todos los conjuntos abiertos en . En tal caso, la variable aleatoria de valor real se llama variable aleatoria de valor real . Además, cuando el espacio es la línea real , entonces dicha variable aleatoria de valor real se llama simplemente variable aleatoria .${\displaystyle E}$ ${\displaystyle {\mathcal {E}}}$ ${\displaystyle {\mathcal {B}}(E)}$${\displaystyle E}$${\displaystyle (E,{\mathcal {E}})}$${\displaystyle E}$${\displaystyle E}$${\displaystyle \mathbb {R} }$

En este caso, el espacio de observación es el conjunto de números reales. Recordemos que es el espacio de probabilidad. Para un espacio de observación real, la función es una variable aleatoria de valor real si${\displaystyle (\Omega ,{\mathcal {F}},P)}$${\displaystyle X\colon \Omega \rightarrow \mathbb {R} }$

${\displaystyle \{\omega :X(\omega )\leq r\}\in {\mathcal {F}}\qquad \forall r\in \mathbb {R} .}$

Esta definición es un caso especial de la anterior porque el conjunto genera la σ-álgebra de Borel en el conjunto de números reales y es suficiente para comprobar la mensurabilidad en cualquier grupo electrógeno. Aquí podemos demostrar la mensurabilidad en este grupo electrógeno utilizando el hecho de que .${\displaystyle \{(-\infty ,r]:r\in \mathbb {R} \}}$${\displaystyle \{\omega :X(\omega )\leq r\}=X^{-1}((-\infty ,r])}$

La distribución de probabilidad de una variable aleatoria se caracteriza a menudo por un pequeño número de parámetros, que también tienen una interpretación práctica. Por ejemplo, a menudo basta con saber cuál es su "valor medio". Esto se refleja en el concepto matemático de valor esperado de una variable aleatoria, denotado como , y también llamado primer momento . En general, no es igual a . Una vez que se conoce el "valor medio", se podría preguntar a qué distancia de este valor medio se encuentran normalmente los valores de , una pregunta que se responde con la varianza y la desviación típica de una variable aleatoria. puede verse intuitivamente como un promedio obtenido de una población infinita, cuyos miembros son evaluaciones particulares de .${\displaystyle \operatorname {E} [X]}$${\displaystyle \operatorname {E} [f(X)]}$${\displaystyle f(\operatorname {E} [X])}$${\displaystyle X}$${\displaystyle \operatorname {E} [X]}$${\displaystyle X}$

Matemáticamente, esto se conoce como el problema (generalizado) de los momentos : para una clase dada de variables aleatorias , encontrar una colección de funciones tales que los valores esperados caractericen completamente la distribución de la variable aleatoria .${\displaystyle X}$${\displaystyle \{f_{i}\}}$${\displaystyle \operatorname {E} [f_{i}(X)]}$${\displaystyle X}$

Los momentos sólo se pueden definir para funciones de valores reales de variables aleatorias (o de valores complejos, etc.). Si la variable aleatoria es en sí misma de valor real, entonces se pueden tomar los momentos de la propia variable, que son equivalentes a los momentos de la función identidad de la variable aleatoria. Sin embargo, incluso para variables aleatorias que no son de valores reales, se pueden tomar los momentos de funciones de valores reales de esas variables. Por ejemplo, para una variable aleatoria categórica X que puede tomar los valores nominales "rojo", "azul" o "verde", se puede construir la función de valor real ; esto utiliza el corchete de Iverson , y tiene el valor 1 si tiene el valor "verde", 0 en caso contrario. Luego, se puede determinar el valor esperado y otros momentos de esta función.${\displaystyle f(X)=X}$${\displaystyle [X={\text{green}}]}$${\displaystyle X}$

Se puede definir una nueva variable aleatoria Y aplicando una función real medible de Borel a los resultados de una variable aleatoria de valor real . Es decir, . La función de distribución acumulativa de es entonces${\displaystyle g\colon \mathbb {R} \rightarrow \mathbb {R} }$${\displaystyle X}$${\displaystyle Y=g(X)}$${\displaystyle Y}$

${\displaystyle F_{Y}(y)=\operatorname {P} (g(X)\leq y).}$

Si la función es invertible (es decir, existe, donde es la función inversa de ) y es creciente o decreciente , entonces la relación anterior se puede extender para obtener${\displaystyle g}$${\displaystyle h=g^{-1}}$${\displaystyle h}$${\displaystyle g}$

${\displaystyle F_{Y}(y)=\operatorname {P} (g(X)\leq y)={\begin{cases}\operatorname {P} (X\leq h(y))=F_{X}(h(y)),&{\text{if }}h=g^{-1}{\text{ increasing}},\\\\\operatorname {P} (X\geq h(y))=1-F_{X}(h(y)),&{\text{if }}h=g^{-1}{\text{ decreasing}}.\end{cases}}}$

Con las mismas hipótesis de invertibilidad de , asumiendo también diferenciabilidad , la relación entre las funciones de densidad de probabilidad se puede encontrar diferenciando ambos lados de la expresión anterior con respecto a , para obtener ^[10]${\displaystyle g}$${\displaystyle y}$

${\displaystyle f_{Y}(y)=f_{X}{\bigl (}h(y){\bigr )}\left|{\frac {dh(y)}{dy}}\right|.}$

Si no hay invertibilidad de pero cada uno admite como máximo un número contable de raíces (es decir, un número finito, o infinito contable, de tales que ), entonces la relación anterior entre las funciones de densidad de probabilidad se puede generalizar con${\displaystyle g}$${\displaystyle y}$${\displaystyle x_{i}}$${\displaystyle y=g(x_{i})}$

${\displaystyle f_{Y}(y)=\sum _{i}f_{X}(g_{i}^{-1}(y))\left|{\frac {dg_{i}^{-1}(y)}{dy}}\right|}$

donde , según el teorema de la función inversa . Las fórmulas para densidades no exigen que sean crecientes.${\displaystyle x_{i}=g_{i}^{-1}(y)}$${\displaystyle g}$

En el enfoque axiomático y teórico de la medida de la probabilidad, si una variable aleatoria en y una función medible de Borel , entonces también es una variable aleatoria en , ya que la composición de funciones medibles también es medible . (Sin embargo, esto no es necesariamente cierto si es medible según Lebesgue . ^{[ cita requerida ]} ) El mismo procedimiento que permitió pasar de un espacio de probabilidad a se puede utilizar para obtener la distribución de .${\displaystyle X}$${\displaystyle \Omega }$ ${\displaystyle g\colon \mathbb {R} \rightarrow \mathbb {R} }$${\displaystyle Y=g(X)}$${\displaystyle \Omega }$${\displaystyle g}$${\displaystyle (\Omega ,P)}$${\displaystyle (\mathbb {R} ,dF_{X})}$${\displaystyle Y}$

Sea una variable aleatoria continua de valor real y sea .${\displaystyle X}$${\displaystyle Y=X^{2}}$

${\displaystyle F_{Y}(y)=\operatorname {P} (X^{2}\leq y).}$

Si , entonces , entonces${\displaystyle y<0}$${\displaystyle P(X^{2}\leq y)=0}$

${\displaystyle F_{Y}(y)=0\qquad {\hbox{if}}\quad y<0.}$

Si , entonces${\displaystyle y\geq 0}$

${\displaystyle \operatorname {P} (X^{2}\leq y)=\operatorname {P} (|X|\leq {\sqrt {y}})=\operatorname {P} (-{\sqrt {y}}\leq X\leq {\sqrt {y}}),}$

entonces

${\displaystyle F_{Y}(y)=F_{X}({\sqrt {y}})-F_{X}(-{\sqrt {y}})\qquad {\hbox{if}}\quad y\geq 0.}$

Supongamos que es una variable aleatoria con una distribución acumulativa${\displaystyle X}$

${\displaystyle F_{X}(x)=P(X\leq x)={\frac {1}{(1+e^{-x})^{\theta }}}}$

donde es un parámetro fijo. Consideremos la variable aleatoria Entonces,${\displaystyle \theta >0}$${\displaystyle Y=\mathrm {log} (1+e^{-X}).}$

${\displaystyle F_{Y}(y)=P(Y\leq y)=P(\mathrm {log} (1+e^{-X})\leq y)=P(X\geq -\mathrm {log} (e^{y}-1)).\,}$

La última expresión se puede calcular en términos de la distribución acumulativa de so${\displaystyle X,}$

${\displaystyle {\begin{aligned}F_{Y}(y)&=1-F_{X}(-\log(e^{y}-1))\\[5pt]&=1-{\frac {1}{(1+e^{\log(e^{y}-1)})^{\theta }}}\\[5pt]&=1-{\frac {1}{(1+e^{y}-1)^{\theta }}}\\[5pt]&=1-e^{-y\theta }.\end{aligned}}}$

que es la función de distribución acumulativa (CDF) de una distribución exponencial .

Supongamos que es una variable aleatoria con una distribución normal estándar , cuya densidad es${\displaystyle X}$

${\displaystyle f_{X}(x)={\frac {1}{\sqrt {2\pi }}}e^{-x^{2}/2}.}$

Consideremos la variable aleatoria Podemos encontrar la densidad utilizando la fórmula anterior para un cambio de variables:${\displaystyle Y=X^{2}.}$

${\displaystyle f_{Y}(y)=\sum _{i}f_{X}(g_{i}^{-1}(y))\left|{\frac {dg_{i}^{-1}(y)}{dy}}\right|.}$

En este caso el cambio no es monótono , porque cada valor de tiene dos valores correspondientes de (uno positivo y otro negativo). Sin embargo, debido a la simetría, ambas mitades se transformarán de manera idéntica, es decir,${\displaystyle Y}$${\displaystyle X}$

${\displaystyle f_{Y}(y)=2f_{X}(g^{-1}(y))\left|{\frac {dg^{-1}(y)}{dy}}\right|.}$

La transformación inversa es

${\displaystyle x=g^{-1}(y)={\sqrt {y}}}$

y su derivada es

${\displaystyle {\frac {dg^{-1}(y)}{dy}}={\frac {1}{2{\sqrt {y}}}}.}$

Entonces,

${\displaystyle f_{Y}(y)=2{\frac {1}{\sqrt {2\pi }}}e^{-y/2}{\frac {1}{2{\sqrt {y}}}}={\frac {1}{\sqrt {2\pi y}}}e^{-y/2}.}$

Esta es una distribución de chi-cuadrado con un grado de libertad .

Supongamos que es una variable aleatoria con una distribución normal , cuya densidad es${\displaystyle X}$

${\displaystyle f_{X}(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-(x-\mu )^{2}/(2\sigma ^{2})}.}$

Consideremos la variable aleatoria Podemos encontrar la densidad utilizando la fórmula anterior para un cambio de variables:${\displaystyle Y=X^{2}.}$

${\displaystyle f_{Y}(y)=\sum _{i}f_{X}(g_{i}^{-1}(y))\left|{\frac {dg_{i}^{-1}(y)}{dy}}\right|.}$

En este caso el cambio no es monótono , porque cada valor de tiene dos valores correspondientes de (uno positivo y otro negativo). Sin embargo, a diferencia del ejemplo anterior, en este caso no hay simetría y tenemos que calcular los dos términos distintos:${\displaystyle Y}$${\displaystyle X}$

${\displaystyle f_{Y}(y)=f_{X}(g_{1}^{-1}(y))\left|{\frac {dg_{1}^{-1}(y)}{dy}}\right|+f_{X}(g_{2}^{-1}(y))\left|{\frac {dg_{2}^{-1}(y)}{dy}}\right|.}$

La transformación inversa es

${\displaystyle x=g_{1,2}^{-1}(y)=\pm {\sqrt {y}}}$

y su derivada es

${\displaystyle {\frac {dg_{1,2}^{-1}(y)}{dy}}=\pm {\frac {1}{2{\sqrt {y}}}}.}$

Entonces,

${\displaystyle f_{Y}(y)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}{\frac {1}{2{\sqrt {y}}}}(e^{-({\sqrt {y}}-\mu )^{2}/(2\sigma ^{2})}+e^{-(-{\sqrt {y}}-\mu )^{2}/(2\sigma ^{2})}).}$

Esta es una distribución chi-cuadrado no central con un grado de libertad .

• La distribución de probabilidad de la suma de dos variables aleatorias independientes es la convolución de cada una de sus distribuciones.
• Las distribuciones de probabilidad no son un espacio vectorial (no están cerradas bajo combinaciones lineales , ya que estas no preservan la no negatividad o la integral total 1), pero sí están cerradas bajo combinaciones convexas , formando así un subconjunto convexo del espacio de funciones (o medidas).

Existen varios sentidos diferentes en los que las variables aleatorias pueden considerarse equivalentes. Dos variables aleatorias pueden ser iguales, casi iguales con seguridad o iguales en distribución.

A continuación se da, en orden creciente de fuerza, la definición precisa de estas nociones de equivalencia.

Si el espacio muestral es un subconjunto de la recta real, las variables aleatorias X e Y son iguales en distribución (denotadas ) si tienen las mismas funciones de distribución:${\displaystyle X{\stackrel {d}{=}}Y}$

${\displaystyle \operatorname {P} (X\leq x)=\operatorname {P} (Y\leq x)\quad {\text{for all }}x.}$

Para que las variables aleatorias tengan una distribución igual, no es necesario que estén definidas en el mismo espacio de probabilidad. Dos variables aleatorias que tengan funciones generadoras de momentos iguales tienen la misma distribución. Esto proporciona, por ejemplo, un método útil para comprobar la igualdad de ciertas funciones de variables aleatorias independientes distribuidas de forma idéntica (IID) . Sin embargo, la función generadora de momentos existe solo para distribuciones que tienen una transformada de Laplace definida .

Dos variables aleatorias X e Y son iguales casi con seguridad (denotado ) si, y solo si, la probabilidad de que sean diferentes es cero :${\displaystyle X\;{\stackrel {\text{a.s.}}{=}}\;Y}$

${\displaystyle \operatorname {P} (X\neq Y)=0.}$

Para todos los efectos prácticos de la teoría de la probabilidad, esta noción de equivalencia es tan fuerte como la igualdad real. Está asociada a la siguiente distancia:

${\displaystyle d_{\infty }(X,Y)=\operatorname {ess} \sup _{\omega }|X(\omega )-Y(\omega )|,}$

donde "ess sup" representa lo esencial supremo en el sentido de la teoría de la medida .

Finalmente, las dos variables aleatorias X e Y son iguales si son iguales como funciones en su espacio medible:

${\displaystyle X(\omega )=Y(\omega )\qquad {\hbox{for all }}\omega .}$

Esta noción suele ser la menos útil en la teoría de la probabilidad porque, en la práctica y en la teoría, el espacio de medida subyacente del experimento rara vez se caracteriza explícitamente o incluso es caracterizable.

Un tema importante en la estadística matemática consiste en la obtención de resultados de convergencia para ciertas secuencias de variables aleatorias; por ejemplo, la ley de los grandes números y el teorema del límite central .

Existen varios sentidos en los que una secuencia de variables aleatorias puede converger a una variable aleatoria . Estos se explican en el artículo sobre convergencia de variables aleatorias .${\displaystyle X_{n}}$${\displaystyle X}$

• "Variable aleatoria", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Zukerman, Moshe (2014), Introducción a la teoría de colas y modelos estocásticos de teletráfico (PDF) , arXiv : 1307.2968
• Zukerman, Moshe (2014), Temas básicos de probabilidad (PDF)