Medida de probabilidad

Parte de una serie sobre estadísticas
Teoría de la probabilidad
Probabilidad Axiomas Determinismo Sistema Indeterminismo Aleatoriedad
Espacio de probabilidad Espacio muestral Evento Eventos colectivamente exhaustivos Evento elemental Exclusividad mutua Resultado Semifallo Experimento El proceso de Bernoulli Distribución de probabilidad Distribución de Bernoulli Distribución binomial Distribución exponencial Distribución normal Distribución de Pareto Distribución de Poisson Medida de probabilidad Variable aleatoria Proceso de Bernoulli Continuo o discreto Valor esperado Diferencia Cadena de Markov Valor observado Paseo aleatorio Proceso estocástico
Evento complementario Probabilidad conjunta Probabilidad marginal Probabilidad condicional
Independencia Independencia condicional Ley de probabilidad total Ley de los grandes números Teorema de Bayes Desigualdad de Boole
Diagrama de Venn Diagrama de árbol
en a mi

En matemáticas , una medida de probabilidad es una función de valor real definida en un conjunto de eventos en un σ-álgebra que satisface propiedades de medida como la aditividad contable . ^[1] La diferencia entre una medida de probabilidad y la noción más general de medida (que incluye conceptos como área o volumen ) es que una medida de probabilidad debe asignar el valor 1 a todo el espacio.

Intuitivamente, la propiedad de aditividad dice que la probabilidad asignada a la unión de dos eventos disjuntos (mutuamente excluyentes) por la medida debe ser la suma de las probabilidades de los eventos; por ejemplo, el valor asignado al resultado "1 o 2" en un lanzamiento de dados debe ser la suma de los valores asignados a los resultados "1" y "2".

Las medidas de probabilidad tienen aplicaciones en diversos campos, desde la física hasta las finanzas y la biología.

Los requisitos para que una función de conjunto sea una medida de probabilidad en un σ-álgebra son los siguientes:${\displaystyle \mu }$

• ${\displaystyle \mu }$debe devolver resultados en el intervalo de unidad que retorna para el conjunto vacío y para todo el espacio.${\displaystyle [0,1],}$${\displaystyle 0}$${\displaystyle 1}$
• ${\displaystyle \mu }$debe satisfacer la propiedad de aditividad contable que para todas las colecciones contables de conjuntos disjuntos por pares :${\displaystyle E_{1},E_{2},\ldots }$$${\displaystyle \mu \left(\bigcup _{i\in \mathbb {N} }E_{i}\right)=\sum _{i\in \mathbb {N} }\mu (E_{i}).}$$

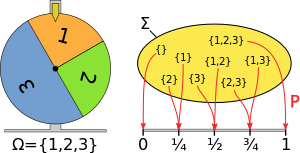
Por ejemplo, dados tres elementos 1, 2 y 3 con probabilidades y el valor asignado es como en el diagrama de la derecha.${\displaystyle 1/4,1/4}$${\displaystyle 1/2,}$${\displaystyle \{1,3\}}$${\displaystyle 1/4+1/2=3/4,}$

La probabilidad condicional basada en la intersección de eventos definida como: ^[2] satisface los requisitos de medida de probabilidad siempre que no sea cero. ^[3]$${\displaystyle \mu (B\mid A)={\frac {\mu (A\cap B)}{\mu (A)}}.}$$${\displaystyle \mu (A)}$

Las medidas de probabilidad son distintas de la noción más general de medidas difusas en las que no existe ningún requisito de que los valores difusos sumen y la propiedad aditiva se reemplaza por una relación de orden basada en la inclusión de conjuntos .${\displaystyle 1,}$

Las medidas de mercado que asignan probabilidades a los espacios del mercado financiero en función de los movimientos reales del mercado son ejemplos de medidas de probabilidad que son de interés en las finanzas matemáticas ; por ejemplo, en la fijación de precios de los derivados financieros . ^[6] Por ejemplo, una medida neutral al riesgo es una medida de probabilidad que supone que el valor actual de los activos es el valor esperado del pago futuro tomado con respecto a esa misma medida neutral al riesgo (es decir, calculado utilizando la función de densidad neutral al riesgo correspondiente), y descontado a la tasa libre de riesgo . Si hay una medida de probabilidad única que debe usarse para fijar el precio de los activos en un mercado, entonces el mercado se denomina mercado completo . ^[7]

No todas las medidas que representan intuitivamente la probabilidad o la casualidad son medidas de probabilidad. Por ejemplo, aunque el concepto fundamental de un sistema en mecánica estadística es un espacio de medida, dichas medidas no siempre son medidas de probabilidad. ^[4] En general, en física estadística, si consideramos enunciados de la forma "la probabilidad de que un sistema S suponga que el estado A es p", la geometría del sistema no siempre conduce a la definición de una medida de probabilidad en condiciones de congruencia , aunque puede hacerlo en el caso de sistemas con un solo grado de libertad. ^[5]

Las medidas de probabilidad también se utilizan en biología matemática . ^[8] Por ejemplo, en el análisis comparativo de secuencias, se puede definir una medida de probabilidad para la probabilidad de que una variante pueda ser permisible para un aminoácido en una secuencia. ^[9]

Los ultrafiltros pueden entenderse como medidas de probabilidad con valores α, lo que permite muchas demostraciones intuitivas basadas en medidas. Por ejemplo, el teorema de Hindman puede demostrarse a partir de una investigación más profunda de estas medidas y, en particular , de su convolución .${\displaystyle \{0,1\}}$

• Medida de Borel  : Medida definida en todos los conjuntos abiertos de un espacio topológico
• Medida difusa  : teoría de medidas generalizadas en la que la propiedad aditiva se reemplaza por la propiedad más débil de la monotonía.Pages displaying wikidata descriptions as a fallback
• Medida de Haar  : medida invariante a la izquierda (o invariante a la derecha) en un grupo topológico localmente compacto
• Medida de Lebesgue  – Concepto de área en cualquier dimensión
• Medida de martingala  – Medida de probabilidadPages displaying short descriptions of redirect targets
• Función de conjunto  : Función de conjuntos a números
• Distribución de probabilidad

• Billingsley, Patrick (1995). Probabilidad y medida . John Wiley. ISBN 0-471-00710-2.
• Ash, Robert B.; Doléans-Dade, Catherine A. (1999). Probabilidad y teoría de la medida . Academic Press. ISBN 0-12-065202-1.
• Distinguir entre medida de probabilidad, función y distribución, Math Stack Exchange

• Medios relacionados con Medida de probabilidad en Wikimedia Commons