Distribución de Pareto

Pareto tipo I

Función de densidad de probabilidad Funciones de densidad de probabilidad de Pareto tipo I para varias con A medida que la distribución se aproxima a donde es la función delta de Dirac .${\estilo de visualización \alpha}$${\displaystyle x_{\mathrm {m} }=1.}$${\displaystyle \alpha \rightarrow \infty,}$${\displaystyle \delta(x-x_{\mathrm {m}}),}$${\estilo de visualización \delta}$
Función de distribución acumulativa Funciones de distribución acumulativa de Pareto tipo I para varios con${\estilo de visualización \alpha}$${\displaystyle x_{\mathrm {m} }=1.}$
Parámetros	${\displaystyle x_{\mathrm {m} }>0}$ escala ( real ) forma (real) ${\displaystyle \alpha >0}$
Apoyo	${\displaystyle x\in[x_{\mathrm {m}},\infty)}$
PDF	${\displaystyle {\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}}$
CDF	${\displaystyle 1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }}$
Cuantil	${\displaystyle x_{\mathrm {m} }{(1-p)}^{-{\frac {1}{\alpha }}}}$
Significar	${\displaystyle {\begin{casos}\infty &{\text{for }}\alpha \leq 1\\{\dfrac {\alpha x_{\mathrm {m} }}{\alpha -1}}&{ \text{para }}\alpha >1\end{casos}}}$
Mediana	${\displaystyle x_{\mathrm {m} }{\sqrt[{\alpha }]{2}}}$
Modo	${\displaystyle x_{\mathrm {m} }}$
Diferencia	${\displaystyle {\begin{casos}\infty &{\text{para }}\alpha \leq 2\\{\dfrac {x_{\mathrm {m} }^{2}\alpha }{(\alpha - 1)^{2}(\alpha -2)}}&{\text{para }}\alpha >2\end{casos}}}$
Oblicuidad	${\displaystyle {\frac {2(1+\alpha )}{\alpha -3}}{\sqrt {\frac {\alpha -2}{\alpha }}}{\text{ para }}\alpha >3}$
Exceso de curtosis	${\displaystyle {\frac {6(\alpha ^{3}+\alpha ^{2}-6\alpha -2)}{\alpha (\alpha -3)(\alpha -4)}}{\text{ para }}\alpha >4}$
Entropía	${\displaystyle \log \left(\left({\frac {x_{\mathrm {m} }}{\alpha }}\right)\,e^{1+{\tfrac {1}{\alpha }}}\right)}$
MGF	no existe
CF	${\displaystyle \alpha (-ix_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t)}$
Información de Fisher	${\displaystyle {\mathcal {I}}(x_{\mathrm {m} },\alpha )={\begin{bmatrix}{\dfrac {\alpha ^{2}}{x_{\mathrm {m} } ^{2}}}&0\\0&{\dfrac {1}{\alpha ^{2}}}\end{bmatrix}}}$
Déficit esperado	${\displaystyle {\frac {x_{m}\alpha }{(1-p)^{\frac {1}{\alpha }}(\alpha -1)}}}$[1]

La distribución de Pareto , llamada así por el ingeniero civil , economista y sociólogo italiano Vilfredo Pareto , ^[2] es una distribución de probabilidad de ley de potencia que se utiliza en la descripción de fenómenos sociales , de control de calidad , científicos , geofísicos , actuariales y muchos otros tipos de fenómenos observables; el principio se aplicó originalmente para describir la distribución de la riqueza en una sociedad, ajustándose a la tendencia de que una gran parte de la riqueza está en manos de una pequeña fracción de la población. ^{[3] [4]} El principio de Pareto o "regla 80-20" que establece que el 80% de los resultados se deben al 20% de las causas fue nombrado en honor a Pareto, pero los conceptos son distintos, y solo las distribuciones de Pareto con valor de forma ( α ) de log ₄ 5 ≈ 1,16 lo reflejan con precisión. La observación empírica ha demostrado que esta distribución 80-20 se ajusta a una amplia gama de casos, incluidos los fenómenos naturales ^[5] y las actividades humanas. ^{[6] [7]}

Si X es una variable aleatoria con una distribución de Pareto (Tipo I), ^[8] entonces la probabilidad de que X sea mayor que algún número x , es decir, la función de supervivencia (también llamada función de cola), está dada por

${\displaystyle {\overline {F}}(x)=\Pr(X>x)={\begin{cases}\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&x\geq x_{\mathrm {m} },\\1&x<x_{\mathrm {m} },\end{cases}}}$

donde x _m es el valor mínimo posible (necesariamente positivo) de X , y α es un parámetro positivo. La distribución de Pareto de tipo I se caracteriza por un parámetro de escala x _m y un parámetro de forma α , que se conoce como índice de cola . Si esta distribución se utiliza para modelar la distribución de la riqueza, entonces el parámetro α se denomina índice de Pareto .

De la definición, la función de distribución acumulativa de una variable aleatoria de Pareto con parámetros α y x _m es

${\displaystyle F_{X}(x)={\begin{cases}1-\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&x\geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\end{cases}}}$

Se deduce (por diferenciación ) que la función de densidad de probabilidad es

${\displaystyle f_{X}(x)={\begin{casos}{\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}&x\ geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\end{casos}}}$

Cuando se representa en ejes lineales, la distribución asume la conocida curva en forma de J que se aproxima a cada uno de los ejes ortogonales de manera asintótica . Todos los segmentos de la curva son autosimilares (sujetos a factores de escala apropiados). Cuando se representa en un gráfico logarítmico-logarítmico , la distribución se representa mediante una línea recta.

• El valor esperado de una variable aleatoria que sigue una distribución de Pareto es

${\displaystyle \operatorname {E} (X)={\begin{cases}\infty &\alpha \leq 1,\\{\frac {\alpha x_{\mathrm {m} }}{\alpha -1} }&\alpha >1.\end{casos}}}$

• La varianza de una variable aleatoria que sigue una distribución de Pareto es

${\displaystyle \operatorname {Var} (X)={\begin{cases}\infty &\alpha \in (1,2],\\\left({\frac {x_{\mathrm {m} }}{\alpha -1}}\right)^{2}{\frac {\alpha }{\alpha -2}}&\alpha >2.\end{cases}}}$

(Si α ≤ 1, la varianza no existe.)

• Los momentos crudos son

${\displaystyle \mu _{n}'={\begin{cases}\infty &\alpha \leq n,\\{\frac {\alpha x_{\mathrm {m} }^{n}}{\alpha -n}}&\alpha >n.\end{cases}}}$

• La función generadora de momentos solo se define para valores no positivos t  ≤ 0 como

${\displaystyle M\left(t;\alpha ,x_{\mathrm {m} }\right)=\operatorname {E} \left[e^{tX}\right]=\alpha (-x_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-x_{\mathrm {m} }t)}$

${\displaystyle M\left(0,\alpha ,x_{\mathrm {m} }\right)=1.}$

Así, como la expectativa no converge en un intervalo abierto que contenga, decimos que la función generadora de momentos no existe.${\displaystyle t=0}$

• La función característica viene dada por

${\displaystyle \varphi (t;\alpha ,x_{\mathrm {m} })=\alpha (-ix_{\mathrm {m} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t),}$

donde Γ( a ,  x ) es la función gamma incompleta .

Los parámetros pueden resolverse utilizando el método de momentos . ^[9]

La distribución de probabilidad condicional de una variable aleatoria distribuida según Pareto, dado el evento de que sea mayor o igual a un número particular  que excede , es una distribución de Pareto con el mismo índice de Pareto  pero con mínimo  en lugar de :${\displaystyle x_{1}}$${\displaystyle x_{\text{m}}}$${\displaystyle \alpha }$${\displaystyle x_{1}}$${\displaystyle x_{\text{m}}}$

${\displaystyle {\text{Pr}}(X\geq x|X\geq x_{1})={\begin{cases}\left({\frac {x_{1}}{x}}\right)^{\alpha }&x\geq x_{1},\\1&x<x_{1}.\end{cases}}}$

Esto implica que el valor esperado condicional (si es finito, es decir ) es proporcional a :${\displaystyle \alpha >1}$${\displaystyle x_{1}}$

${\displaystyle {\text{E}}(X|X\geq x_{1})\propto x_{1}.}$

En el caso de variables aleatorias que describen la vida útil de un objeto, esto significa que la esperanza de vida es proporcional a la edad y se denomina efecto Lindy o Ley de Lindy. ^[10]

Supóngase que hay variables aleatorias independientes distribuidas de forma idéntica cuya distribución de probabilidad se sustenta en el intervalo para algún . Supóngase que para todos , las dos variables aleatorias y son independientes. Entonces la distribución común es una distribución de Pareto. ^{[ cita requerida ]}${\displaystyle X_{1},X_{2},X_{3},\dotsc }$ ${\displaystyle [x_{\text{m}},\infty )}$${\displaystyle x_{\text{m}}>0}$${\displaystyle n}$${\displaystyle \min\{X_{1},\dotsc ,X_{n}\}}$${\displaystyle (X_{1}+\dotsb +X_{n})/\min\{X_{1},\dotsc ,X_{n}\}}$

La media geométrica ( G ) es ^[11]

${\displaystyle G=x_{\text{m}}\exp \left({\frac {1}{\alpha }}\right).}$

La media armónica ( H ) es ^[11]

${\displaystyle H=x_{\text{m}}\left(1+{\frac {1}{\alpha }}\right).}$

La característica distribución curva de " cola larga ", cuando se representa gráficamente en una escala lineal, enmascara la simplicidad subyacente de la función cuando se representa gráficamente en un gráfico logarítmico-logarítmico , que luego toma la forma de una línea recta con gradiente negativo: De la fórmula para la función de densidad de probabilidad se deduce que para x ≥ x _m ,

${\displaystyle \log f_{X}(x)=\log \left(\alpha {\frac {x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}\right)=\log(\alpha x_{\mathrm {m} }^{\alpha })-(\alpha +1)\log x.}$

Como α es positivo, el gradiente −( α  + 1) es negativo.

Existe una jerarquía ^{[8] [12]} de distribuciones de Pareto conocidas como distribuciones de Pareto tipo I, II, III, IV y de Feller–Pareto. ^{[8] [12] [13]} La distribución de Pareto tipo IV contiene las distribuciones de Pareto tipo I–III como casos especiales. La distribución de Feller–Pareto ^{[12] [14]} generaliza la distribución de Pareto tipo IV.

La jerarquía de la distribución de Pareto se resume en la siguiente tabla comparando las funciones de supervivencia (CDF complementaria).

Cuando μ = 0, la distribución de Pareto tipo II también se conoce como distribución Lomax . ^[15]

En esta sección, el símbolo x _m ​​, utilizado anteriormente para indicar el valor mínimo de x , se reemplaza por  σ .

Distribuciones de Pareto

	${\displaystyle {\overline {F}}(x)=1-F(x)}$	Apoyo	Parámetros
Tipo I	${\displaystyle \left[{\frac {x}{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq \sigma }$	${\displaystyle \sigma >0,\alpha }$
Tipo II	${\displaystyle \left[1+{\frac {x-\mu }{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma >0,\alpha }$
Lomax	${\displaystyle \left[1+{\frac {x}{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq 0}$	${\displaystyle \sigma >0,\alpha }$
Tipo III	${\displaystyle \left[1+\left({\frac {x-\mu }{\sigma }}\right)^{1/\gamma }\right]^{-1}}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma ,\gamma >0}$
Tipo IV	${\displaystyle \left[1+\left({\frac {x-\mu }{\sigma }}\right)^{1/\gamma }\right]^{-\alpha }}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma ,\gamma >0,\alpha }$

El parámetro de forma α es el índice de cola, μ es la ubicación, σ es la escala, γ es un parámetro de desigualdad. Algunos casos especiales de tipo Pareto (IV) son

${\displaystyle P(IV)(\sigma ,\sigma ,1,\alpha )=P(I)(\sigma ,\alpha ),}$

${\displaystyle P(IV)(\mu ,\sigma ,1,\alpha )=P(II)(\mu ,\sigma ,\alpha ),}$

${\displaystyle P(IV)(\mu ,\sigma ,\gamma ,1)=P(III)(\mu ,\sigma ,\gamma ).}$

La finitud de la media y la existencia y finitud de la varianza dependen del índice de cola α (índice de desigualdad γ ). En particular, los momentos δ fraccionarios son finitos para algún δ > 0, como se muestra en la tabla siguiente, donde δ no es necesariamente un número entero.

Momentos de las distribuciones de Pareto I–IV (caso μ = 0)

	${\displaystyle \operatorname {E} [X]}$	Condición	${\displaystyle \operatorname {E} [X^{\delta }]}$	Condición
Tipo I	${\displaystyle {\frac {\sigma \alpha }{\alpha -1}}}$	${\displaystyle \alpha >1}$	${\displaystyle {\frac {\sigma ^{\delta }\alpha }{\alpha -\delta }}}$	${\displaystyle \delta <\alpha }$
Tipo II	${\displaystyle {\frac {\sigma }{\alpha -1}}+\mu }$	${\displaystyle \alpha >1}$	${\displaystyle {\frac {\sigma ^{\delta }\Gamma (\alpha -\delta )\Gamma (1+\delta )}{\Gamma (\alpha )}}}$	${\displaystyle 0<\delta <\alpha }$
Tipo III	${\displaystyle \sigma \Gamma (1-\gamma )\Gamma (1+\gamma )}$	${\displaystyle -1<\gamma <1}$	${\displaystyle \sigma ^{\delta }\Gamma (1-\gamma \delta )\Gamma (1+\gamma \delta )}$	${\displaystyle -\gamma ^{-1}<\delta <\gamma ^{-1}}$
Tipo IV	${\displaystyle {\frac {\sigma \Gamma (\alpha -\gamma )\Gamma (1+\gamma )}{\Gamma (\alpha )}}}$	${\displaystyle -1<\gamma <\alpha }$	${\displaystyle {\frac {\sigma ^{\delta }\Gamma (\alpha -\gamma \delta )\Gamma (1+\gamma \delta )}{\Gamma (\alpha )}}}$	${\displaystyle -\gamma ^{-1}<\delta <\alpha /\gamma }$

Feller ^{[12] [14]} define una variable de Pareto mediante la transformación U  =  Y ⁻¹  − 1 de una variable aleatoria beta , Y , cuya función de densidad de probabilidad es

${\displaystyle f(y)={\frac {y^{\gamma _{1}-1}(1-y)^{\gamma _{2}-1}}{B(\gamma _{1},\gamma _{2})}},\qquad 0<y<1;\gamma _{1},\gamma _{2}>0,}$

donde B ( ) es la función beta . Si

${\displaystyle W=\mu +\sigma (Y^{-1}-1)^{\gamma },\qquad \sigma >0,\gamma >0,}$

entonces W tiene una distribución de Feller-Pareto FP( μ , σ , γ , γ ₁ , γ ₂ ). ^[8]

Si y son variables Gamma independientes , otra construcción de una variable Feller-Pareto (FP) es ^[16]${\displaystyle U_{1}\sim \Gamma (\delta _{1},1)}$${\displaystyle U_{2}\sim \Gamma (\delta _{2},1)}$

${\displaystyle W=\mu +\sigma \left({\frac {U_{1}}{U_{2}}}\right)^{\gamma }}$

y escribimos W ~ FP( μ , σ , γ , δ ₁ , δ ₂ ). Los casos especiales de la distribución de Feller-Pareto son

${\displaystyle FP(\sigma ,\sigma ,1,1,\alpha )=P(I)(\sigma ,\alpha )}$

${\displaystyle FP(\mu ,\sigma ,1,1,\alpha )=P(II)(\mu ,\sigma ,\alpha )}$

${\displaystyle FP(\mu ,\sigma ,\gamma ,1,1)=P(III)(\mu ,\sigma ,\gamma )}$

${\displaystyle FP(\mu ,\sigma ,\gamma ,1,\alpha )=P(IV)(\mu ,\sigma ,\gamma ,\alpha ).}$

Cuando una variable aleatoria sigue una distribución de Pareto, su inversa sigue una distribución de Pareto inversa. La distribución de Pareto inversa es equivalente a una distribución de potencia ^[17]${\displaystyle Y}$${\displaystyle X=1/Y}$

${\displaystyle Y\sim \mathrm {Pa} (\alpha ,x_{m})={\frac {\alpha x_{m}^{\alpha }}{y^{\alpha +1}}}\quad (y\geq x_{m})\quad \Leftrightarrow \quad X\sim \mathrm {iPa} (\alpha ,x_{m})=\mathrm {Power} (x_{m}^{-1},\alpha )={\frac {\alpha x^{\alpha -1}}{(x_{m}^{-1})^{\alpha }}}\quad (0<x\leq x_{m}^{-1})}$

La distribución de Pareto está relacionada con la distribución exponencial de la siguiente manera. Si X tiene una distribución de Pareto con un mínimo x _m ​​y un índice  α , entonces

${\displaystyle Y=\log \left({\frac {X}{x_{\mathrm {m} }}}\right)}$

se distribuye exponencialmente con un parámetro de velocidad  α . De manera equivalente, si Y se distribuye exponencialmente con una velocidad  α , entonces

${\displaystyle x_{\mathrm {m} }e^{Y}}$

se distribuye según Pareto con un mínimo x _m ​​y un índice  α .

Esto se puede demostrar utilizando las técnicas estándar de cambio de variable:

${\displaystyle {\begin{aligned}\Pr(Y<y)&=\Pr \left(\log \left({\frac {X}{x_{\mathrm {m} }}}\right)<y\right)\\&=\Pr(X<x_{\mathrm {m} }e^{y})=1-\left({\frac {x_{\mathrm {m} }}{x_{\mathrm {m} }e^{y}}}\right)^{\alpha }=1-e^{-\alpha y}.\end{aligned}}}$

La última expresión es la función de distribución acumulativa de una distribución exponencial con tasa  α .

La distribución de Pareto se puede construir mediante distribuciones exponenciales jerárquicas. ^[18] Sea y . Entonces tenemos y, como resultado, .${\displaystyle \phi |a\sim {\text{Exp}}(a)}$${\displaystyle \eta |\phi \sim {\text{Exp}}(\phi )}$${\displaystyle p(\eta |a)={\frac {a}{(a+\eta )^{2}}}}$${\displaystyle a+\eta \sim {\text{Pareto}}(a,1)}$

De manera más general, si (parametrización de velocidad de forma) y , entonces .${\displaystyle \lambda \sim {\text{Gamma}}(\alpha ,\beta )}$${\displaystyle \eta |\lambda \sim {\text{Exp}}(\lambda )}$${\displaystyle \beta +\eta \sim {\text{Pareto}}(\beta ,\alpha )}$

Equivalentemente, si y , entonces .${\displaystyle Y\sim {\text{Gamma}}(\alpha ,1)}$${\displaystyle X\sim {\text{Exp}}(1)}$${\displaystyle x_{\text{m}}\!\left(1+{\frac {X}{Y}}\right)\sim {\text{Pareto}}(x_{\text{m}},\alpha )}$

La distribución de Pareto y la distribución log-normal son distribuciones alternativas para describir los mismos tipos de cantidades. Una de las conexiones entre las dos es que ambas son distribuciones de la distribución exponencial de variables aleatorias distribuidas de acuerdo con otras distribuciones comunes, respectivamente la distribución exponencial y la distribución normal . (Véase la sección anterior.)

La distribución de Pareto es un caso especial de la distribución de Pareto generalizada , que es una familia de distribuciones de forma similar, pero que contiene un parámetro adicional de tal manera que el soporte de la distribución está acotado por debajo (en un punto variable), o acotado tanto por encima como por debajo (donde ambos son variables), siendo la distribución de Lomax un caso especial. Esta familia también contiene las distribuciones exponenciales desplazadas y no desplazadas .

La distribución de Pareto con escala y forma es equivalente a la distribución de Pareto generalizada con ubicación , escala y forma y, a la inversa, se puede obtener la distribución de Pareto a partir del GPD tomando y si .${\displaystyle x_{m}}$${\displaystyle \alpha }$${\displaystyle \mu =x_{m}}$${\displaystyle \sigma =x_{m}/\alpha }$${\displaystyle \xi =1/\alpha }$${\displaystyle x_{m}=\sigma /\xi }$${\displaystyle \alpha =1/\xi }$${\displaystyle \xi >0}$

Pareto acotado

Parámetros	${\displaystyle L>0}$ Ubicación ( real ) Ubicación ( real ) ${\displaystyle H>L}$ ${\displaystyle \alpha >0}$ forma (real)
Apoyo	${\displaystyle L\leqslant x\leqslant H}$
PDF	${\displaystyle {\frac {\alpha L^{\alpha }x^{-\alpha -1}}{1-\left({\frac {L}{H}}\right)^{\alpha }}}}$
CDF	${\displaystyle {\frac {1-L^{\alpha }x^{-\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}}$
Significar	${\displaystyle {\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot \left({\frac {\alpha }{\alpha -1}}\right)\cdot \left({\frac {1}{L^{\alpha -1}}}-{\frac {1}{H^{\alpha -1}}}\right),\alpha \neq 1}$ ${\displaystyle {\frac {{H}{L}}{{H}-{L}}}\ln {\frac {H}{L}},\alpha =1}$
Mediana	${\displaystyle L\left(1-{\frac {1}{2}}\left(1-\left({\frac {L}{H}}\right)^{\alpha }\right)\right)^{-{\frac {1}{\alpha }}}}$
Diferencia	${\displaystyle {\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot \left({\frac {\alpha }{\alpha -2}}\right)\cdot \left({\frac {1}{L^{\alpha -2}}}-{\frac {1}{H^{\alpha -2}}}\right),\alpha \neq 2}$${\displaystyle {\frac {2{H}^{2}{L}^{2}}{{H}^{2}-{L}^{2}}}\ln {\frac {H}{L}},\alpha =2}$ (este es el segundo momento crudo, no la varianza)
Oblicuidad	${\displaystyle {\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot {\frac {\alpha (L^{k-\alpha }-H^{k-\alpha })}{(\alpha -k)}},\alpha \neq j}$ (este es el k-ésimo momento bruto, no la asimetría)

La distribución de Pareto acotada (o truncada) tiene tres parámetros: α , L y H . Al igual que en la distribución de Pareto estándar, α determina la forma. L denota el valor mínimo y H denota el valor máximo.

La función de densidad de probabilidad es

${\displaystyle {\frac {\alpha L^{\alpha }x^{-\alpha -1}}{1-\left({\frac {L}{H}}\right)^{\alpha }}}}$,

donde L  ≤  x  ≤  H , y α  > 0.

Si U se distribuye uniformemente en (0, 1), entonces aplicando el método de transformada inversa ^[19]

${\displaystyle U={\frac {1-L^{\alpha }x^{-\alpha }}{1-({\frac {L}{H}})^{\alpha }}}}$

${\displaystyle x=\left(-{\frac {UH^{\alpha }-UL^{\alpha }-H^{\alpha }}{H^{\alpha }L^{\alpha }}}\right)^{-{\frac {1}{\alpha }}}}$

es una distribución de Pareto acotada.

El propósito de las distribuciones de Pareto simétricas y simétricas cero es capturar alguna distribución estadística especial con un pico de probabilidad agudo y colas de probabilidad largas simétricas. Estas dos distribuciones se derivan de la distribución de Pareto. Las colas de probabilidad largas normalmente significan que la probabilidad decae lentamente y se pueden usar para ajustar una variedad de conjuntos de datos. Pero si la distribución tiene una estructura simétrica con dos colas de decaimiento lento, Pareto no podría hacerlo. Entonces se aplica la distribución de Pareto simétrica o la distribución de Pareto simétrica cero en su lugar. ^[20]

La función de distribución acumulativa (CDF) de la distribución de Pareto simétrica se define de la siguiente manera: ^[20]

${\displaystyle F(X)=P(x<X)={\begin{cases}{\tfrac {1}{2}}({b \over 2b-X})^{a}&X<b\\1-{\tfrac {1}{2}}({\tfrac {b}{X}})^{a}&X\geq b\end{cases}}}$

La función de densidad de probabilidad (PDF) correspondiente es: ^[20]

${\displaystyle p(x)={ab^{a} \over 2(b+\left\vert x-b\right\vert )^{a+1}},X\in R}$

Esta distribución tiene dos parámetros: a y b. Es simétrica respecto de b. Por lo tanto, la esperanza matemática es b. Cuando esto sucede, tiene varianza como se muestra a continuación:

${\displaystyle E((x-b)^{2})=\int _{-\infty }^{\infty }(x-b)^{2}p(x)dx={2b^{2} \over (a-2)(a-1)}}$

La CDF de la distribución Pareto simétrica cero (ZSP) se define de la siguiente manera:

${\displaystyle F(X)=P(x<X)={\begin{cases}{\tfrac {1}{2}}({b \over b-X})^{a}&X<0\\1-{\tfrac {1}{2}}({\tfrac {b}{b+X}})^{a}&X\geq 0\end{cases}}}$

El PDF correspondiente es:

${\displaystyle p(x)={ab^{a} \over 2(b+\left\vert x\right\vert )^{a+1}},X\in R}$

Esta distribución es simétrica respecto del cero. El parámetro a está relacionado con la tasa de disminución de la probabilidad y (a/2b) representa la magnitud máxima de la probabilidad. ^[20]

La distribución de Pareto univariante se ha extendido a una distribución de Pareto multivariante . ^[21]

La función de verosimilitud para los parámetros de distribución de Pareto α y x _m , dada una muestra independiente x = ( x ₁ ,  x ₂ , ...,  x _n ), es

${\displaystyle L(\alpha ,x_{\mathrm {m} })=\prod _{i=1}^{n}\alpha {\frac {x_{\mathrm {m} }^{\alpha }}{x_{i}^{\alpha +1}}}=\alpha ^{n}x_{\mathrm {m} }^{n\alpha }\prod _{i=1}^{n}{\frac {1}{x_{i}^{\alpha +1}}}.}$

Por lo tanto, la función de verosimilitud logarítmica es

${\displaystyle \ell (\alpha ,x_{\mathrm {m} })=n\ln \alpha +n\alpha \ln x_{\mathrm {m} }-(\alpha +1)\sum _{i=1}^{n}\ln x_{i}.}$

Se puede observar que aumenta monótonamente con x _m , es decir, cuanto mayor sea el valor de x _m , mayor será el valor de la función de verosimilitud. Por lo tanto, como x ≥ x _m , concluimos que${\displaystyle \ell (\alpha ,x_{\mathrm {m} })}$

${\displaystyle {\widehat {x}}_{\mathrm {m} }=\min _{i}{x_{i}}.}$

Para encontrar el estimador de α , calculamos la derivada parcial correspondiente y determinamos dónde es cero:

${\displaystyle {\frac {\partial \ell }{\partial \alpha }}={\frac {n}{\alpha }}+n\ln x_{\mathrm {m} }-\sum _{i=1}^{n}\ln x_{i}=0.}$

Por lo tanto, el estimador de máxima verosimilitud para α es:

${\displaystyle {\widehat {\alpha }}={\frac {n}{\sum _{i}\ln(x_{i}/{\widehat {x}}_{\mathrm {m} })}}.}$

El error estadístico esperado es: ^[22]

${\displaystyle \sigma ={\frac {\widehat {\alpha }}{\sqrt {n}}}.}$

Malik (1970) ^[23] proporciona la distribución conjunta exacta de . En particular, y son independientes y es de Pareto con parámetro de escala x _m y parámetro de forma nα , mientras que tiene una distribución gamma inversa con parámetros de forma y escala n  − 1 y nα , respectivamente.${\displaystyle ({\hat {x}}_{\mathrm {m} },{\hat {\alpha }})}$${\displaystyle {\hat {x}}_{\mathrm {m} }}$${\displaystyle {\hat {\alpha }}}$${\displaystyle {\hat {x}}_{\mathrm {m} }}$${\displaystyle {\hat {\alpha }}}$

Vilfredo Pareto utilizó originalmente esta distribución para describir la asignación de riqueza entre individuos, ya que parecía mostrar bastante bien la forma en que una porción mayor de la riqueza de cualquier sociedad es propiedad de un porcentaje menor de la gente en esa sociedad. También la utilizó para describir la distribución del ingreso. ^[4] Esta idea a veces se expresa de manera más simple como el principio de Pareto o la "regla 80-20", que dice que el 20% de la población controla el 80% de la riqueza. ^[24] Como señala Michael Hudson ( The Collapse of Antiquity [2023] p. 85 y n.7) "un corolario matemático [es] que el 10% tendría el 65% de la riqueza, y el 5% tendría la mitad de la riqueza nacional". Sin embargo, la regla 80-20 corresponde a un valor particular de α y, de hecho, los datos de Pareto sobre los impuestos a la renta británicos en su Cours d'économie politique indican que aproximadamente el 30% de la población tenía aproximadamente el 70% de los ingresos. ^{[ cita requerida ]} El gráfico de la función de densidad de probabilidad (PDF) al comienzo de este artículo muestra que la "probabilidad" o fracción de la población que posee una pequeña cantidad de riqueza por persona es bastante alta y luego disminuye de manera constante a medida que aumenta la riqueza. (Sin embargo, la distribución de Pareto no es realista para la riqueza del extremo inferior. De hecho, el patrimonio neto puede incluso ser negativo). Esta distribución no se limita a describir la riqueza o los ingresos, sino a muchas situaciones en las que se encuentra un equilibrio en la distribución de lo "pequeño" a lo "grande". Los siguientes ejemplos a veces se consideran aproximadamente distribuidos según Pareto:

• Las cuatro variables de la restricción presupuestaria del hogar: consumo, ingresos laborales, ingresos de capital y riqueza. ^[25]
• Los tamaños de los asentamientos humanos (pocas ciudades, muchas aldeas/pueblos) ^{[26] [27]}
• Distribución del tamaño de los archivos del tráfico de Internet que utiliza el protocolo TCP (muchos archivos más pequeños, pocos más grandes) ^[26]
• Tasas de error de la unidad de disco duro ^[28]
• Cúmulos de condensado de Bose-Einstein cerca del cero absoluto ^[29]

• Los valores de las reservas de petróleo en los yacimientos petrolíferos (unos pocos yacimientos grandes , muchos yacimientos pequeños ) ^[26]
• La distribución de la longitud de los trabajos asignados a las supercomputadoras (unas pocas grandes, muchas pequeñas) ^[30]
• Los rendimientos de precios estandarizados de las acciones individuales ^[26]
• Tamaños de partículas de arena ^[26]
• El tamaño de los meteoritos
• Gravedad de las grandes pérdidas por accidentes en determinadas líneas de negocio, como responsabilidad civil general, seguros de automóviles comerciales y compensación de trabajadores. ^{[31] [32]}
• Cantidad de tiempo que un usuario de Steam pasa jugando a distintos juegos. (Algunos juegos se juegan mucho, pero la mayoría casi nunca). [2] ^{[ ¿ Investigación original? ]}
• En hidrología, la distribución de Pareto se aplica a eventos extremos, como las precipitaciones máximas anuales de un día y las descargas de los ríos. ^[33] La imagen azul ilustra un ejemplo de ajuste de la distribución de Pareto a las precipitaciones máximas anuales de un día clasificadas, mostrando también el cinturón de confianza del 90 % basado en la distribución binomial . Los datos de precipitaciones se representan trazando posiciones como parte del análisis de frecuencia acumulada .
• En la confiabilidad de la distribución de servicios eléctricos (el 80% de los minutos interrumpidos por el cliente ocurren aproximadamente en el 20% de los días de un año determinado).

La distribución de Pareto es una distribución de probabilidad continua. La ley de Zipf , también llamada a veces distribución zeta , es una distribución discreta, que separa los valores en una clasificación simple. Ambas son una ley de potencia simple con un exponente negativo, escalada de modo que sus distribuciones acumuladas sean iguales a 1. La de Zipf se puede derivar de la distribución de Pareto si los valores (ingresos) se agrupan en rangos de modo que el número de personas en cada grupo siga un patrón de 1/rango. La distribución se normaliza definiendo de modo que donde es el número armónico generalizado . Esto hace que la función de densidad de probabilidad de Zipf se pueda derivar de la de Pareto.${\displaystyle x}$${\displaystyle N}$${\displaystyle x_{m}}$${\displaystyle \alpha x_{\mathrm {m} }^{\alpha }={\frac {1}{H(N,\alpha -1)}}}$${\displaystyle H(N,\alpha -1)}$

${\displaystyle f(x)={\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}={\frac {1}{x^{s}H(N,s)}}}$

donde y es un número entero que representa un rango de 1 a N, donde N es el nivel de ingresos más alto. Por lo tanto, una persona (o palabra, enlace de sitio web o ciudad) seleccionada al azar de una población (o idioma, Internet o país) tiene una probabilidad de clasificarse en .${\displaystyle s=\alpha -1}$${\displaystyle x}$${\displaystyle f(x)}$${\displaystyle x}$

La " ley 80-20 ", según la cual el 20% de la población recibe el 80% de los ingresos totales, y el 20% del 20% más rico recibe el 80% de ese 80%, y así sucesivamente, se cumple precisamente cuando el índice de Pareto es . Este resultado se puede derivar de la fórmula de la curva de Lorenz que se muestra a continuación. Además, se ha demostrado ^[34] que las siguientes fórmulas son matemáticamente equivalentes:${\displaystyle \alpha =\log _{4}5={\cfrac {\log _{10}5}{\log _{10}4}}\approx 1.161}$

• El ingreso se distribuye según una distribución de Pareto con índice α  > 1.
• Existe un número 0 ≤  p  ≤ 1/2 tal que el 100 p  % de todas las personas recibe el 100(1 −  p )% de todos los ingresos, y de manera similar para cada número real (no necesariamente entero) n  > 0, el 100 p ⁿ  % de todas las personas recibe el 100(1 −  p ) ⁿ porcentaje de todos los ingresos. α y p están relacionados por

${\displaystyle 1-{\frac {1}{\alpha }}={\frac {\ln(1-p)}{\ln(p)}}={\frac {\ln((1-p)^{n})}{\ln(p^{n})}}}$

Esto no se aplica sólo a los ingresos, sino también a la riqueza o a cualquier otra cosa que pueda modelarse mediante esta distribución.

Esto excluye las distribuciones de Pareto en las que 0 <  α  ≤ 1, que, como se señaló anteriormente, tienen un valor esperado infinito y, por lo tanto, no pueden modelar razonablemente la distribución del ingreso.

La ley de la raíz cuadrada de Price se presenta a veces como una propiedad de la distribución de Pareto o como algo similar a ella. Sin embargo, la ley solo se cumple en el caso de que . Nótese que, en este caso, la cantidad total y esperada de riqueza no están definidas, y la regla solo se aplica asintóticamente a muestras aleatorias. El principio de Pareto extendido mencionado anteriormente es una regla mucho más general.${\displaystyle \alpha =1}$

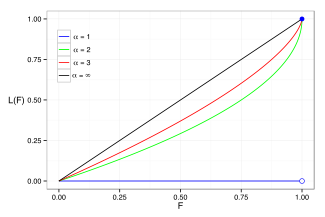
La curva de Lorenz se utiliza a menudo para caracterizar las distribuciones de ingresos y riqueza. Para cualquier distribución, la curva de Lorenz L ( F ) se escribe en términos de la función de densidad de probabilidad (PDF ) o la función de flujo de efectivo (CDF) F como

${\displaystyle L(F)={\frac {\int _{x_{\mathrm {m} }}^{x(F)}xf(x)\,dx}{\int _{x_{\mathrm {m} }}^{\infty }xf(x)\,dx}}={\frac {\int _{0}^{F}x(F')\,dF'}{\int _{0}^{1}x(F')\,dF'}}}$

donde x ( F ) es la inversa de la CDF. Para la distribución de Pareto,

${\displaystyle x(F)={\frac {x_{\mathrm {m} }}{(1-F)^{\frac {1}{\alpha }}}}}$

y se calcula que la curva de Lorenz es

${\displaystyle L(F)=1-(1-F)^{1-{\frac {1}{\alpha }}},}$

Como el denominador es infinito, se obtiene que L = 0. En el gráfico de la derecha se muestran ejemplos de la curva de Lorenz para varias distribuciones de Pareto.${\displaystyle 0<\alpha \leq 1}$

Según Oxfam (2016) las 62 personas más ricas tienen tanta riqueza como la mitad más pobre de la población mundial. ^[35] Podemos estimar el índice de Pareto que se aplicaría a esta situación. Si ε es igual, tenemos:${\displaystyle 62/(7\times 10^{9})}$

${\displaystyle L(1/2)=1-L(1-\varepsilon )}$

o

${\displaystyle 1-(1/2)^{1-{\frac {1}{\alpha }}}=\varepsilon ^{1-{\frac {1}{\alpha }}}}$

La solución es que α es igual a aproximadamente 1,15 y que aproximadamente el 9% de la riqueza está en manos de cada uno de los dos grupos. Pero en realidad el 69% más pobre de la población adulta mundial posee solo alrededor del 3% de la riqueza. ^[36]

El coeficiente de Gini es una medida de la desviación de la curva de Lorenz respecto de la línea de equidistribución, que es una línea que conecta [0, 0] y [1, 1], que se muestra en negro ( α  = ∞) en el gráfico de Lorenz de la derecha. Específicamente, el coeficiente de Gini es el doble del área entre la curva de Lorenz y la línea de equidistribución. El coeficiente de Gini para la distribución de Pareto se calcula entonces (para ) como${\displaystyle \alpha \geq 1}$

${\displaystyle G=1-2\left(\int _{0}^{1}L(F)\,dF\right)={\frac {1}{2\alpha -1}}}$

(véase Aaberge 2005).

Se pueden generar muestras aleatorias utilizando el muestreo por transformada inversa . Dada una variable aleatoria U extraída de la distribución uniforme en el intervalo unitario [0, 1], la variable T dada por

${\displaystyle T={\frac {x_{\mathrm {m} }}{U^{1/\alpha }}}}$

se distribuye según Pareto. ^[37]

• Ley de Bradford  – Patrón de referencias en revistas científicas
• Ley de Gutenberg-Richter  : ley en sismología que describe la frecuencia y magnitud de los terremotos
• Efecto Mateo  : los ricos se vuelven más ricos y los pobres más pobres
• Análisis de Pareto  : Principio estadístico sobre la relación entre los efectos y las causasPages displaying short descriptions of redirect targets
• Eficiencia de Pareto  : asignación débilmente óptima de recursos
• Interpolación de Pareto  : método para estimar la mediana de una población
• Distribuciones de probabilidad de ley de potencia  : relación funcional entre dos cantidades
• Ley de Sturgeon  : “El noventa por ciento de todo es basura”
• Modelo de generación de tráfico  : flujo simulado de datos en una red de comunicacionesPages displaying wikidata descriptions as a fallback
• Ley de Zipf  – Distribución de probabilidad
• Distribución de cola pesada  – Distribución de probabilidad

• MO Lorenz (1905). "Métodos de medición de la concentración de la riqueza". Publications of the American Statistical Association . 9 (70): 209–19. Bibcode :1905PAmSA...9..209L. doi :10.2307/2276207. JSTOR  2276207. S2CID  154048722.
• Pareto, Vilfredo (1965). Librairie Droz (ed.). Ecrits sur la courbe de la répartition de la richesse . Obras completas : T. III. pag. 48.ISBN​ 9782600040211.

• Pareto, Vilfredo (1895). "La legge della domanda". Giornale degli Economisti . 10 : 59–68.
• Pareto, Vilfredo (1896). "Curses de economía política". doi :10.1177/000271629700900314. S2CID  143528002. {{cite journal}}: Requiere citar revista |journal=( ayuda )

• "Distribución de Pareto", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Distribución de Pareto". MathWorld .
• Aabergé, Rolf (mayo de 2005). "La familia nuclear de Gini". Conferencia internacional en homenaje a dos eminentes científicos sociales (PDF) .

• Crovella, Mark E. ; Bestavros, Azer (diciembre de 1997). Autosimilitud en el tráfico de la World Wide Web: evidencia y posibles causas (PDF) . IEEE/ACM Transactions on Networking. Vol. 5. págs. 835–846. Archivado desde el original (PDF) el 2016-03-04 . Consultado el 2019-02-25 .

• syntraf1.c es un programa en C para generar tráfico de paquetes sintéticos con un tamaño de ráfaga de Pareto limitado y un tiempo entre ráfagas exponencial.