Exponenciación

Operaciones aritméticas en a mi

Adición (+) ${\displaystyle \scriptstyle \left.{\begin{matriz}\scriptstyle {\text{término}}\,+\,{\text{término}}\\\scriptstyle {\text{suma}}\,+\,{\text{suma}}\\\scriptstyle {\text{addend}}\,+\,{\text{addend}}\\\scriptstyle {\text{augend}}\,+\,{\text{addend}}\end{matriz}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{suma}}}$ Resta (−) ${\displaystyle \scriptstyle \left.{\begin{matriz}\scriptstyle {\text{término}}\,-\,{\text{término}}\\\scriptstyle {\text{minuendo}}\,-\,{\text{sustraendo}}\end{matriz}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{diferencia}}}$ Multiplicación (×) ${\displaystyle \scriptstyle \left.{\begin{matriz}\scriptstyle {\text{factor}}\,\times \,{\text{factor}}\\\scriptstyle {\text{multiplicador}}\,\times \,{\text{multiplicando}}\end{matriz}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{producto}}}$ División (÷) ${\displaystyle \scriptstyle \left.{\begin{matriz}\scriptstyle {\frac {\scriptstyle {\text{dividendo}}}{\scriptstyle {\text{divisor}}}}\\[1ex]\scriptstyle {\frac {\scriptstyle {\text{numerador}}}{\scriptstyle {\text{denominador}}}}\end{matriz}}\right\}\,=\,}$ ${\displaystyle \scriptstyle \left\{{\begin{matriz}\scriptstyle {\text{fracción}}\\\scriptstyle {\text{cociente}}\\\scriptstyle {\text{razón}}\end{matriz}}\right.}$ Exponenciación (^) ${\displaystyle \scriptstyle \left.{\begin{matriz}\scriptstyle {\text{base}}^{\text{exponente}}\\\scriptstyle {\text{base}}^{\text{potencia}}\end{matriz}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{poder}}}$ raíz n -ésima (√) ${\displaystyle \scriptstyle {\sqrt[{\text{degree}}]{\scriptstyle {\text{radicand}}}}\,=\,}$ ${\displaystyle \scriptstyle {\text{root}}}$ Logarithm (log) ${\displaystyle \scriptstyle \log _{\text{base}}({\text{anti-logarithm}})\,=\,}$ ${\displaystyle \scriptstyle {\text{logarithm}}}$

v t e

En matemáticas , la exponenciación es una operación que involucra dos números : la base y el exponente o potencia . La exponenciación se escribe como b ⁿ , donde b es la base y n es la potencia ; a menudo se dice como " b a la potencia n ". ^[1] Cuando n es un entero positivo , la exponenciación corresponde a la multiplicación repetida de la base: es decir, b ⁿ es el producto de multiplicar n bases: ^[1] En particular, . $${\displaystyle b^{n}=\underbrace {b\times b\times \dots \times b\times b} _{n{\text{ times}}}.}$$${\displaystyle b^{1}=b}$

El exponente se muestra generalmente como un superíndice a la derecha de la base como b ⁿ o en código informático como b^n, y también se puede llamar " b elevado a la n -ésima potencia", " b a la potencia de n ", "la n -ésima potencia de b ", ^[2] o más brevemente " b a la n ".

La definición anterior de inmediatamente implica varias propiedades, en particular la regla de multiplicación: ^{[nb 1]}${\displaystyle b^{n}}$

$${\displaystyle {\begin{aligned}b^{n}\times b^{m}&=\underbrace {b\times \dots \times b} _{n{\text{ times}}}\times \underbrace {b\times \dots \times b} _{m{\text{ times}}}\\[1ex]&=\underbrace {b\times \dots \times b} _{n+m{\text{ times}}}\ =\ b^{n+m}.\end{aligned}}}$$

Es decir, al multiplicar una base elevada a una potencia por la misma base elevada a otra potencia, las potencias se suman. Extendiendo esta regla a la potencia cero se obtiene , y dividiendo ambos lados por se obtiene . Es decir, la regla de multiplicación implica la definición Un argumento similar implica la definición para potencias enteras negativas: Es decir, extendiendo la regla de multiplicación se obtiene . Dividiendo ambos lados por se obtiene . Esto también implica la definición para potencias fraccionarias: Por ejemplo, , es decir , que es la definición de raíz cuadrada: .${\displaystyle b^{0}\times b^{n}=b^{0+n}=b^{n}}$${\displaystyle b^{n}}$${\displaystyle b^{0}=b^{n}/b^{n}=1}$$${\displaystyle b^{0}=1.}$$$${\displaystyle b^{-n}=1/b^{n}.}$$${\displaystyle b^{-n}\times b^{n}=b^{-n+n}=b^{0}=1}$${\displaystyle b^{n}}$${\displaystyle b^{-n}=1/b^{n}}$$${\displaystyle b^{n/m}={\sqrt[{m}]{b^{n}}}.}$$${\displaystyle b^{1/2}\times b^{1/2}=b^{1/2\,+\,1/2}=b^{1}=b}$${\displaystyle (b^{1/2})^{2}=b}$${\displaystyle b^{1/2}={\sqrt {b}}}$

La definición de exponenciación se puede ampliar de forma natural (conservando la regla de multiplicación) para definir para cualquier base real positiva y cualquier exponente real . Definiciones más complejas permiten utilizar como base o exponente a determinados tipos de matrices .${\displaystyle b^{x}}$${\displaystyle b}$${\displaystyle x}$

La exponenciación se utiliza ampliamente en muchos campos, incluidos la economía , la biología , la química , la física y la informática , con aplicaciones como el interés compuesto , el crecimiento poblacional , la cinética de las reacciones químicas , el comportamiento de las ondas y la criptografía de clave pública .

El término exponente tiene su origen en el latín exponentem , participio presente de exponere , que significa "poner adelante". ^[3] El término potencia ( latín : potentia, potestas, dignitas ) es una traducción errónea ^{[4] [5]} del griego antiguo δύναμις ( dúnamis , aquí: "amplificación" ^[4] ) utilizado por el matemático griego Euclides para el cuadrado de una línea, ^[6] siguiendo a Hipócrates de Quíos . ^[7]

En The Sand Reckoner , Arquímedes demostró la ley de los exponentes, 10 ^a · 10 ^b = 10 ^{a + b} , necesaria para manipular potencias de 10. ^[8] Luego utilizó potencias de 10 para estimar la cantidad de granos de arena que pueden contener el universo.

En el siglo IX, el matemático persa Al-Khwarizmi utilizó los términos مَال ( māl , "posesiones", "propiedad") para un cuadrado —los musulmanes, "como la mayoría de los matemáticos de aquellos tiempos y de épocas anteriores, pensaban en un número cuadrado como una representación de un área, especialmente de tierra, por lo tanto, propiedad" ^[9] —y كَعْبَة ( Kaʿbah , "cubo") para un cubo , que los matemáticos islámicos posteriores representaron en notación matemática como las letras mīm (m) y kāf (k), respectivamente, en el siglo XV, como se ve en la obra de Abu'l-Hasan ibn Ali al-Qalasadi . ^[10]

Nicolas Chuquet utilizó una forma de notación exponencial en el siglo XV, por ejemplo 12 ² para representar 12 x ² . ^[11] Esto fue utilizado más tarde por Henricus Grammateus y Michael Stifel en el siglo XVI. A finales del siglo XVI, Jost Bürgi utilizaría números romanos para exponentes de una manera similar a la de Chuquet, por ejemploiii4para 4 x ³ . ^[12]

La palabra exponente fue acuñada en 1544 por Michael Stifel. ^{[13] [14]} En el siglo XVI, Robert Recorde utilizó los términos cuadrado, cubo, zenzizenzic ( cuarta potencia ), sursólido (quinto), zenzicubo (sexto), segundo sursólido (séptimo) y zenzizenzizenzic (octavo). ^[9] Bicuadrado también se ha utilizado para referirse a la cuarta potencia.

En 1636, James Hume utilizó en esencia la notación moderna, cuando en L'algèbre de Viète escribió A ⁱⁱⁱ por A ³ . ^[15] A principios del siglo XVII, la primera forma de nuestra notación exponencial moderna fue introducida por René Descartes en su texto titulado La Géométrie ; allí, la notación se introduce en el Libro I. ^[16]

Yo designo... aa , o un ² al multiplicar a por sí mismo; y un ³ al multiplicarlo una vez más por a , y así hasta el infinito.

—  René Descartes, La geometría

Algunos matemáticos (como Descartes) utilizaban exponentes solo para potencias mayores que dos, prefiriendo representar los cuadrados como multiplicaciones repetidas. Así, escribían los polinomios , por ejemplo, como ax + bxx + cx ³ + d .

Samuel Jeake introdujo el término índices en 1696. ^[6] El término involución se usaba como sinónimo del término índices , pero su uso había disminuido ^[17] y no debe confundirse con su significado más común .

En 1748, Leonhard Euler introdujo exponentes variables y, implícitamente, exponentes no enteros escribiendo:

Consideremos exponenciales o potencias en las que el propio exponente es una variable. Es claro que cantidades de este tipo no son funciones algebraicas , ya que en ellas los exponentes deben ser constantes. ^[18]

La expresión b ² = b · b se llama "el cuadrado de b " o " b al cuadrado", porque el área de un cuadrado con lado b es b ² . (Es cierto que también podría llamarse " b elevado a la segunda potencia", pero "el cuadrado de b " y " b elevado al cuadrado" están tan arraigados por la tradición y la conveniencia que " b elevado a la segunda potencia" tiende a sonar inusual o torpe.)

De manera similar, la expresión b ³ = b · b · b se llama "el cubo de b " o " b al cubo", porque el volumen de un cubo con lados b es b ³ .

Cuando un exponente es un entero positivo , ese exponente indica cuántas copias de la base se multiplican entre sí. Por ejemplo, 3 ⁵ = 3 · 3 · 3 · 3 · 3 = 243. La base 3 aparece 5 veces en la multiplicación, porque el exponente es 5. Aquí, 243 es la quinta potencia de 3 , o 3 elevado a la quinta potencia .

La palabra "elevado" suele omitirse, y a veces también "potencia", por lo que 3 ⁵ puede leerse simplemente "3 elevado a 5", o "3 a la 5".

La operación de exponenciación con exponentes enteros puede definirse directamente a partir de operaciones aritméticas elementales .

La definición de la exponenciación como una multiplicación iterada se puede formalizar mediante el uso de inducción , ^[19] y esta definición se puede utilizar tan pronto como se tenga una multiplicación asociativa :

El caso base es

${\displaystyle b^{1}=b}$

y la recurrencia es

${\displaystyle b^{n+1}=b^{n}\cdot b.}$

La asociatividad de la multiplicación implica que para cualesquiera números enteros positivos m y n ,

${\displaystyle b^{m+n}=b^{m}\cdot b^{n},}$

y

${\displaystyle (b^{m})^{n}=b^{mn}.}$

Como se mencionó anteriormente, un número (distinto de cero) elevado a la potencia 0 es 1 : ^{[20] [1]}

${\displaystyle b^{0}=1.}$

Este valor también se obtiene por la convención del producto vacío , que se puede utilizar en cualquier estructura algebraica con una multiplicación que tenga una identidad . De esta manera la fórmula

${\displaystyle b^{m+n}=b^{m}\cdot b^{n}}$

También es válido para .${\displaystyle n=0}$

El caso de 0 ⁰ es controvertido. En contextos en los que solo se consideran potencias enteras, generalmente se asigna el valor 1 a 0 ^0, pero, en caso contrario, la elección de asignarle un valor y qué valor asignar puede depender del contexto. Para obtener más detalles, consulte Cero elevado a la potencia de cero .

La exponenciación con exponentes negativos se define por la siguiente identidad, que es válida para cualquier entero n y b distinto de cero :

${\displaystyle b^{-n}={\frac {1}{b^{n}}}}$. ^[1]

Elevar 0 a un exponente negativo no está definido pero, en algunas circunstancias, puede interpretarse como infinito ( ). ^[21]${\displaystyle \infty }$

Esta definición de exponenciación con exponentes negativos es la única que permite extender la identidad a exponentes negativos (consideremos el caso ).${\displaystyle b^{m+n}=b^{m}\cdot b^{n}}$${\displaystyle m=-n}$

La misma definición se aplica a los elementos invertibles en un monoide multiplicativo , es decir, una estructura algebraica , con una multiplicación asociativa y una identidad multiplicativa denotada 1 (por ejemplo, las matrices cuadradas de una dimensión dada). En particular, en una estructura de este tipo, el inverso de un elemento invertible x se denota de manera estándar${\displaystyle x^{-1}.}$

Las siguientes identidades , a menudo llamadasLas reglas de los exponentes se aplican a todos los exponentes enteros, siempre que la base no sea cero:^[1]

${\displaystyle {\begin{aligned}b^{m}\cdot b^{n}&=b^{m+n}\\\left(b^{m}\right)^{n}&=b^{m\cdot n}\\b^{n}\cdot c^{n}&=(b\cdot c)^{n}\end{aligned}}}$

A diferencia de la suma y la multiplicación, la exponenciación no es conmutativa : por ejemplo, , pero al invertir los operandos se obtiene el valor diferente . También a diferencia de la suma y la multiplicación, la exponenciación no es asociativa : por ejemplo, (2 ³ ) ² = 8 ² = 64 , mientras que 2 ^{(3 2 )} = 2 ⁹ = 512 . Sin paréntesis, el orden convencional de operaciones para la exponenciación serial en notación de superíndice es de arriba hacia abajo (o asociativa por la derecha ), no de abajo hacia arriba ^{[22] [23] [24]} (o asociativa por la izquierda ). Es decir,${\displaystyle 2^{3}=8}$${\displaystyle 3^{2}=9}$

${\displaystyle b^{p^{q}}=b^{\left(p^{q}\right)},}$

que, en general, es diferente de

${\displaystyle \left(b^{p}\right)^{q}=b^{pq}.}$

Las potencias de una suma normalmente se pueden calcular a partir de las potencias de los sumandos mediante la fórmula binomial.

${\displaystyle (a+b)^{n}=\sum _{i=0}^{n}{\binom {n}{i}}a^{i}b^{n-i}=\sum _{i=0}^{n}{\frac {n!}{i!(n-i)!}}a^{i}b^{n-i}.}$

Sin embargo, esta fórmula es verdadera solo si los sumandos conmutan (es decir, que ab = ba ), lo que está implícito si pertenecen a una estructura que es conmutativa . De lo contrario, si a y b son, digamos, matrices cuadradas del mismo tamaño, esta fórmula no se puede utilizar. De ello se deduce que en álgebra computacional , muchos algoritmos que involucran exponentes enteros deben cambiarse cuando las bases de exponenciación no conmutan. Algunos sistemas de álgebra computacional de propósito general usan una notación diferente (a veces ^^ en lugar de ^ ) para la exponenciación con bases no conmutativas, que entonces se llama exponenciación no conmutativa .

Para los números enteros no negativos n y m , el valor de n ^m es el número de funciones de un conjunto de m elementos a un conjunto de n elementos (véase exponenciación cardinal ). Dichas funciones se pueden representar como m - tuplas de un conjunto de n elementos (o como palabras de m - letras de un alfabeto de n - letras). En la siguiente tabla se dan algunos ejemplos de valores particulares de m y n :

En el sistema de numeración decimal , las potencias enteras de 10 se escriben como el dígito 1 seguido o precedido por una cantidad de ceros determinada por el signo y la magnitud del exponente. Por ejemplo,10 ³ =1000 y10 ⁻⁴ =0,0001 .

La exponenciación con base 10 se utiliza en notación científica para indicar números grandes o pequeños. Por ejemplo,299 792 458  m/s (la velocidad de la luz en el vacío, en metros por segundo ) se puede escribir como2,997 924 58 × 10 ⁸  m/s y luego se aproxima como2,998 × 10 ⁸  m/s .

Los prefijos del SI basados ​​en potencias de 10 también se utilizan para describir cantidades pequeñas o grandes. Por ejemplo, el prefijo kilo significa10 ³ =1000 , entonces un kilómetro es1000 metros .

Las primeras potencias negativas de 2 tienen nombres especiales: es un medio ; es un cuarto .${\displaystyle 2^{-1}}$${\displaystyle 2^{-2}}$

Las potencias de 2 aparecen en ^la teoría de conjuntos , ya que un conjunto con n miembros tiene un conjunto potencia , el conjunto de todos sus subconjuntos , que tiene 2n miembros.

Las potencias enteras de 2 son importantes en informática . Las potencias enteras positivas 2 ⁿ dan el número de valores posibles para un número binario entero de n bits ; por ejemplo, un byte puede tomar 2 ⁸ = 256 valores diferentes. El sistema de numeración binario expresa cualquier número como una suma de potencias de 2 , y lo denota como una secuencia de 0 y 1 , separados por un punto binario , donde 1 indica una potencia de 2 que aparece en la suma; el exponente está determinado por el lugar de este 1 : los exponentes no negativos son el rango del 1 a la izquierda del punto (empezando desde 0 ), y los exponentes negativos están determinados por el rango a la derecha del punto.

Toda potencia de uno es igual a: 1 ⁿ = 1 .

Para un exponente positivo n > 0 , la n- ésima potencia de cero es cero: 0 ⁿ = 0 . Para un exponente negativo, no está definido. ${\displaystyle 0^{-n}=1/0^{n}=1/0}$

La expresión 0 ⁰ se define como o se deja sin definir.${\displaystyle \lim _{x\to 0}x^{x}=1}$

Como un número negativo multiplicado por otro negativo es positivo, tenemos:

${\displaystyle (-1)^{n}=\left\{{\begin{array}{rl}1&{\text{for even }}n,\\-1&{\text{for odd }}n.\\\end{array}}\right.}$

Por este motivo, las potencias de −1 son útiles para expresar secuencias alternadas . Para un análisis similar de las potencias del número complejo i , véase § Raíces n-ésimas de un número complejo .

El límite de una secuencia de potencias de un número mayor que uno diverge; en otras palabras, la secuencia crece sin límite:

b ⁿ → ∞ cuando n → ∞ cuando b > 1

Esto puede leerse como " b elevado a n tiende a +∞ cuando n tiende a infinito cuando b es mayor que uno".

Las potencias de un número con valor absoluto menor que uno tienden a cero:

b ⁿ → 0 cuando n → ∞ cuando | b | < 1

Cualquier potencia de uno es siempre uno:

b ⁿ = 1 para todo n para b = 1

Las potencias de un número negativo alternan entre positivo y negativo a medida que n alterna entre par e impar, y por lo tanto no tienden a ningún límite a medida que n crece.${\displaystyle b\leq -1}$

Si el número exponencial varía mientras tiende a 1 a medida que el exponente tiende a infinito, entonces el límite no es necesariamente uno de los anteriores. Un caso particularmente importante es

(1 + 1/ n ) ⁿ → e como n → ∞

Véase § Función exponencial a continuación.

Otros límites, en particular los de las expresiones que toman una forma indeterminada , se describen en el § Límites de las potencias más adelante.

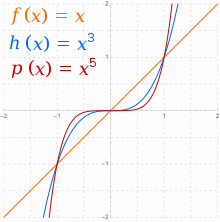
Las funciones reales de la forma , donde , a veces se denominan funciones potencia. ^[25] Cuando es un número entero y , existen dos familias principales: para par, y para impar. En general , para , cuando es par tenderá hacia el infinito positivo con un aumento de , y también hacia el infinito positivo con un descenso de . Todos los gráficos de la familia de funciones potencia pares tienen la forma general de , aplanándose más en el medio a medida que aumenta. ^[26] Las funciones con este tipo de simetría ( ) se denominan funciones pares .${\displaystyle f(x)=cx^{n}}$${\displaystyle c\neq 0}$${\displaystyle n}$${\displaystyle n\geq 1}$${\displaystyle n}$${\displaystyle n}$${\displaystyle c>0}$${\displaystyle n}$${\displaystyle f(x)=cx^{n}}$${\displaystyle x}$${\displaystyle x}$${\displaystyle y=cx^{2}}$${\displaystyle n}$ ${\displaystyle f(-x)=f(x)}$

Cuando es impar, el comportamiento asintótico de se invierte de positivo a negativo . Para , también tenderá hacia el infinito positivo con el aumento de , pero hacia el infinito negativo con la disminución de . Todos los gráficos de la familia de funciones de potencia impares tienen la forma general de , aplanándose más en el medio a medida que aumenta y perdiendo toda planitud allí en la línea recta para . Las funciones con este tipo de simetría ( ) se denominan funciones impares .${\displaystyle n}$${\displaystyle f(x)}$${\displaystyle x}$${\displaystyle x}$${\displaystyle c>0}$${\displaystyle f(x)=cx^{n}}$${\displaystyle x}$${\displaystyle x}$${\displaystyle y=cx^{3}}$${\displaystyle n}$${\displaystyle n=1}$${\displaystyle f(-x)=-f(x)}$

Para , el comportamiento asintótico opuesto es cierto en cada caso. ^[26]${\displaystyle c<0}$

Si x es un número real no negativo , y n es un entero positivo, o denota la única raíz n- ésima real no negativa de x , es decir, el único número real no negativo y tal que${\displaystyle x^{1/n}}$${\displaystyle {\sqrt[{n}]{x}}}$${\displaystyle y^{n}=x.}$

Si x es un número real positivo, y es un número racional , con p y q > 0 enteros, entonces se define como${\displaystyle {\frac {p}{q}}}$${\textstyle x^{p/q}}$

${\displaystyle x^{\frac {p}{q}}=\left(x^{p}\right)^{\frac {1}{q}}=(x^{\frac {1}{q}})^{p}.}$

La igualdad a la derecha se puede derivar estableciendo y escribiendo${\displaystyle y=x^{\frac {1}{q}},}$${\displaystyle (x^{\frac {1}{q}})^{p}=y^{p}=\left((y^{p})^{q}\right)^{\frac {1}{q}}=\left((y^{q})^{p}\right)^{\frac {1}{q}}=(x^{p})^{\frac {1}{q}}.}$

Si r es un número racional positivo, 0 ^r = 0 , por definición.

Todas estas definiciones son necesarias para extender la identidad a exponentes racionales.${\displaystyle (x^{r})^{s}=x^{rs}}$

Por otra parte, existen problemas con la extensión de estas definiciones a bases que no son números reales positivos. Por ejemplo, un número real negativo tiene una raíz n- ésima real, que es negativa, si n es impar , y no tiene raíz real si n es par. En el último caso, no se puede satisfacer la raíz n- ésima compleja que se elija para la identidad . Por ejemplo,${\displaystyle x^{\frac {1}{n}},}$${\displaystyle (x^{a})^{b}=x^{ab}}$

${\displaystyle \left((-1)^{2}\right)^{\frac {1}{2}}=1^{\frac {1}{2}}=1\neq (-1)^{2\cdot {\frac {1}{2}}}=(-1)^{1}=-1.}$

Consulte § Exponentes reales y § Potencias no enteras de números complejos para obtener detalles sobre la forma en que se pueden resolver estos problemas.

Para los números reales positivos, la exponenciación a potencias reales se puede definir de dos maneras equivalentes, ya sea extendiendo las potencias racionales a los reales por continuidad ( § Límites de exponentes racionales , a continuación), o en términos del logaritmo de la base y la función exponencial ( § Potencias mediante logaritmos , a continuación). El resultado es siempre un número real positivo, y las identidades y propiedades mostradas anteriormente para exponentes enteros siguen siendo verdaderas con estas definiciones para exponentes reales. La segunda definición se utiliza más comúnmente, ya que se generaliza directamente a exponentes complejos .

Por otra parte, la exponenciación a una potencia real de un número real negativo es mucho más difícil de definir de manera consistente, ya que puede ser no real y tener varios valores. Se puede elegir uno de estos valores, llamado valor principal , pero no hay elección del valor principal para el cual se define la identidad.

${\displaystyle \left(b^{r}\right)^{s}=b^{rs}}$

es verdadera; véase § Falla de identidades de potencia y logaritmo . Por lo tanto, la exponenciación con una base que no es un número real positivo generalmente se considera como una función multivaluada .

Dado que cualquier número irracional puede expresarse como el límite de una secuencia de números racionales, la exponenciación de un número real positivo b con un exponente real arbitrario x puede definirse por continuidad con la regla ^[27]

${\displaystyle b^{x}=\lim _{r(\in \mathbb {Q} )\to x}b^{r}\quad (b\in \mathbb {R} ^{+},\,x\in \mathbb {R} ),}$

donde el límite se toma únicamente sobre valores racionales de r . Este límite existe para cada b positivo y cada x real .

Por ejemplo, si x = π , la representación decimal no terminal π = 3,14159... y la monotonía de las potencias racionales se puede utilizar para obtener intervalos acotados por potencias racionales que sean tan pequeños como se desee, y deben contener${\displaystyle b^{\pi }:}$

${\displaystyle \left[b^{3},b^{4}\right],\left[b^{3.1},b^{3.2}\right],\left[b^{3.14},b^{3.15}\right],\left[b^{3.141},b^{3.142}\right],\left[b^{3.1415},b^{3.1416}\right],\left[b^{3.14159},b^{3.14160}\right],\ldots }$

Por lo tanto, los límites superiores y los límites inferiores de los intervalos forman dos secuencias que tienen el mismo límite, denotado${\displaystyle b^{\pi }.}$

Esto define para cada b positivo y x real como una función continua de b y x . Véase también Expresión bien definida . ^[28]${\displaystyle b^{x}}$

La función exponencial puede definirse como donde es el número de Euler , pero para evitar el razonamiento circular , esta definición no se puede utilizar aquí. En su lugar, damos una definición independiente de la función exponencial y de , basándonos únicamente en potencias enteras positivas (multiplicación repetida). A continuación, esbozamos la prueba de que esto concuerda con la definición anterior:${\displaystyle x\mapsto e^{x},}$${\displaystyle e\approx 2.718}$${\displaystyle \exp(x),}$${\displaystyle e=\exp(1)}$${\displaystyle \exp(x)=e^{x}.}$

Hay muchas formas equivalentes de definir la función exponencial , una de ellas es

${\displaystyle \exp(x)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}.}$

Se tiene y la identidad exponencial (o regla de multiplicación) también se cumple, ya que${\displaystyle \exp(0)=1,}$${\displaystyle \exp(x)\exp(y)=\exp(x+y)}$

${\displaystyle \exp(x)\exp(y)=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}\left(1+{\frac {y}{n}}\right)^{n}=\lim _{n\rightarrow \infty }\left(1+{\frac {x+y}{n}}+{\frac {xy}{n^{2}}}\right)^{n},}$

y el término de segundo orden no afecta el límite, dando como resultado .${\displaystyle {\frac {xy}{n^{2}}}}$${\displaystyle \exp(x)\exp(y)=\exp(x+y)}$

El número de Euler se puede definir como . De las ecuaciones anteriores se deduce que cuando x es un entero (esto resulta de la definición de multiplicación repetida de la exponenciación). Si x es real, resulta de las definiciones dadas en las secciones anteriores, utilizando la identidad exponencial si x es racional y la continuidad de la función exponencial en caso contrario.${\displaystyle e=\exp(1)}$${\displaystyle \exp(x)=e^{x}}$${\displaystyle \exp(x)=e^{x}}$

El límite que define la función exponencial converge para cada valor complejo de x y, por lo tanto, se puede utilizar para extender la definición de y, por lo tanto, de los números reales a cualquier argumento complejo z . Esta función exponencial extendida aún satisface la identidad exponencial y se utiliza comúnmente para definir la exponenciación para bases y exponentes complejos.${\displaystyle \exp(z)}$${\displaystyle e^{z},}$

La definición de e ^x como función exponencial permite definir b ^x para cada número real positivo b , en términos de función exponencial y logarítmica . En concreto, el hecho de que el logaritmo natural ln( x ) sea la inversa de la función exponencial e ^x significa que se tiene

${\displaystyle b=\exp(\ln b)=e^{\ln b}}$

para cada b > 0. Para preservar la identidad se debe tener${\displaystyle (e^{x})^{y}=e^{xy},}$

${\displaystyle b^{x}=\left(e^{\ln b}\right)^{x}=e^{x\ln b}}$

Por lo tanto, se puede utilizar como definición alternativa de b ^x para cualquier número real positivo b . Esto concuerda con la definición dada anteriormente utilizando exponentes racionales y continuidad, con la ventaja de extenderse directamente a cualquier exponente complejo.${\displaystyle e^{x\ln b}}$

Si b es un número real positivo, la exponenciación con base b y exponente complejo z se define por medio de la función exponencial con argumento complejo (ver el final del § Función exponencial , arriba) como

${\displaystyle b^{z}=e^{(z\ln b)},}$

donde denota el logaritmo natural de b .${\displaystyle \ln b}$

Esto satisface la identidad

${\displaystyle b^{z+t}=b^{z}b^{t},}$

En general, no está definida, ya que b ^z no es un número real. Si se le da un significado a la exponenciación de un número complejo (ver § Potencias no enteras de números complejos , más adelante), se tiene, en general,${\textstyle \left(b^{z}\right)^{t}}$

${\displaystyle \left(b^{z}\right)^{t}\neq b^{zt},}$

a menos que z sea real o t sea un entero.

Fórmula de Euler ,

${\displaystyle e^{iy}=\cos y+i\sin y,}$

permite expresar la forma polar de en términos de las partes reales e imaginarias de z , es decir${\displaystyle b^{z}}$

${\displaystyle b^{x+iy}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)),}$

donde el valor absoluto del factor trigonométrico es uno. Esto resulta de

${\displaystyle b^{x+iy}=b^{x}b^{iy}=b^{x}e^{iy\ln b}=b^{x}(\cos(y\ln b)+i\sin(y\ln b)).}$

En las secciones anteriores, la exponenciación con exponentes no enteros se ha definido sólo para bases reales positivas. Para otras bases, las dificultades aparecen ya con el caso aparentemente simple de raíces n -ésimas, es decir, de exponentes donde n es un entero positivo. Aunque la teoría general de la exponenciación con exponentes no enteros se aplica a raíces n- ésimas , este caso merece ser considerado primero, ya que no necesita utilizar logaritmos complejos y, por lo tanto, es más fácil de entender.${\displaystyle 1/n,}$

Todo número complejo distinto de cero z puede escribirse en forma polar como

${\displaystyle z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),}$

donde es el valor absoluto de z , y es su argumento . El argumento se define hasta un múltiplo entero de 2 π ; esto significa que, si es el argumento de un número complejo, entonces es también un argumento del mismo número complejo para cada entero .${\displaystyle \rho }$${\displaystyle \theta }$${\displaystyle \theta }$${\displaystyle \theta +2k\pi }$${\displaystyle k}$

La forma polar del producto de dos números complejos se obtiene multiplicando los valores absolutos y sumando los argumentos. De ello se deduce que la forma polar de una raíz n -ésima de un número complejo se puede obtener tomando la raíz n -ésima del valor absoluto y dividiendo su argumento por n :

${\displaystyle \left(\rho e^{i\theta }\right)^{\frac {1}{n}}={\sqrt[{n}]{\rho }}\,e^{\frac {i\theta }{n}}.}$

Si se suma a , el número complejo no cambia, pero esto se suma al argumento de la raíz n -ésima y proporciona una nueva raíz n -ésima. Esto se puede hacer n veces y proporciona las raíces n - ésimas del número complejo.${\displaystyle 2\pi }$${\displaystyle \theta }$${\displaystyle 2i\pi /n}$

Es habitual elegir una de las n n -ésimas raíces como raíz principal . La elección común es elegir la n -ésima raíz para la cual es decir, la n -ésima raíz que tiene la parte real más grande y, si hay dos, la que tiene la parte imaginaria positiva. Esto hace que la n -ésima raíz principal sea una función continua en todo el plano complejo, excepto para valores reales negativos del radicando . Esta función es igual a la n -ésima raíz habitual para radicandos reales positivos. Para radicandos reales negativos y exponentes impares, la n -ésima raíz principal no es real, aunque la n -ésima raíz habitual sí lo es. La continuación analítica muestra que la n -ésima raíz principal es la única función compleja diferenciable que extiende la n -ésima raíz habitual al plano complejo sin los números reales no positivos.${\displaystyle -\pi <\theta \leq \pi ,}$

Si el número complejo se mueve alrededor del cero incrementando su argumento, después de un incremento de , el número complejo vuelve a su posición inicial, y sus raíces n -ésimas se permutan circularmente (se multiplican por ). Esto demuestra que no es posible definir una función raíz n- ésima que sea continua en todo el plano complejo.${\displaystyle 2\pi ,}$$e^{2i\pi /n}$

Las raíces n- ésimas de la unidad son los n números complejos tales que w ⁿ = 1 , donde n es un entero positivo. Surgen en diversas áreas de las matemáticas, como en la transformada de Fourier discreta o en las soluciones algebraicas de ecuaciones algebraicas ( resolvente de Lagrange ).

Las raíces n n ésimas de la unidad son las n primeras potencias de , es decir Las raíces n ésimas de la unidad que tienen esta propiedad generadora se llaman raíces n ésimas primitivas de la unidad ; tienen la forma con k coprimo con n . La única raíz cuadrada primitiva de la unidad es las raíces cuartas primitivas de la unidad son y${\displaystyle \omega =e^{\frac {2\pi i}{n}}}$${\displaystyle 1=\omega ^{0}=\omega ^{n},\omega =\omega ^{1},\omega ^{2},\omega ^{n-1}.}$${\displaystyle \omega ^{k}=e^{\frac {2k\pi i}{n}},}$ ${\displaystyle -1;}$${\displaystyle i}$${\displaystyle -i.}$

Las n -ésimas raíces de la unidad permiten expresar todas las n -ésimas raíces de un número complejo z como los n productos de una n -ésima raíz dada de z con una n -ésima raíz de la unidad.

Geométricamente, las raíces n -ésimas de la unidad se encuentran en el círculo unitario del plano complejo en los vértices de un n -gono regular con un vértice en el número real 1.

Como el número es la raíz n- ésima primitiva de la unidad con el argumento positivo más pequeño , se le llama raíz n- ésima primitiva principal de la unidad , a veces abreviada como raíz n- ésima principal de la unidad , aunque esta terminología puede confundirse con el valor principal de , que es 1. ^{[29] [30] [31]}${\displaystyle e^{\frac {2k\pi i}{n}}}$${\displaystyle 1^{1/n}}$

La definición de exponenciación con bases complejas conduce a dificultades similares a las descritas en la sección anterior, excepto que, en general, hay infinitos valores posibles para . Por lo tanto, o bien se define un valor principal , que no es continuo para los valores de z que son reales y no positivos, o bien se define como una función multivaluada .$z^{w}$$z^{w}$

En todos los casos, el logaritmo complejo se utiliza para definir la exponenciación compleja como

${\displaystyle z^{w}=e^{w\log z},}$

donde es la variante del logaritmo complejo que se utiliza, que es una función o una función multivaluada tal que${\displaystyle \log z}$

${\displaystyle e^{\log z}=z}$

para cada z en su dominio de definición .

El valor principal del logaritmo complejo es la única función continua, comúnmente denotada de manera que, para cada número complejo z distinto de cero ,${\displaystyle \log ,}$

${\displaystyle e^{\log z}=z,}$

y el argumento de z satisface

${\displaystyle -\pi <\operatorname {Arg} z\leq \pi .}$

El valor principal del logaritmo complejo no está definido porque es discontinuo en valores reales negativos de z y es holomorfo (es decir, complejo diferenciable) en cualquier otro lugar. Si z es real y positivo, el valor principal del logaritmo complejo es el logaritmo natural:${\displaystyle z=0,}$${\displaystyle \log z=\ln z.}$

El valor principal de se define como donde es el valor principal del logaritmo.${\displaystyle z^{w}}$${\displaystyle z^{w}=e^{w\log z},}$${\displaystyle \log z}$

La función es holomorfa excepto en la vecindad de los puntos donde z es real y no positivo.${\displaystyle (z,w)\to z^{w}}$

Si z es real y positivo, el valor principal de es igual a su valor habitual definido anteriormente. Si donde n es un entero, este valor principal es el mismo que el definido anteriormente.${\displaystyle z^{w}}$${\displaystyle w=1/n,}$

En algunos contextos, existe un problema con la discontinuidad de los valores principales de y en los valores reales negativos de z . En este caso, es útil considerar estas funciones como funciones multivaluadas .${\displaystyle \log z}$${\displaystyle z^{w}}$

Si denota uno de los valores del logaritmo multivaluado (normalmente su valor principal), los demás valores son donde k es cualquier entero. De manera similar, si es un valor de la potenciación, entonces los demás valores están dados por${\displaystyle \log z}$${\displaystyle 2ik\pi +\log z,}$${\displaystyle z^{w}}$

${\displaystyle e^{w(2ik\pi +\log z)}=z^{w}e^{2ik\pi w},}$

donde k es cualquier entero.

Diferentes valores de k dan diferentes valores de a menos que w sea un número racional , es decir, existe un entero d tal que dw es un entero. Esto resulta de la periodicidad de la función exponencial, más específicamente, que si y solo si es un múltiplo entero de${\displaystyle z^{w}}$${\displaystyle e^{a}=e^{b}}$${\displaystyle a-b}$${\displaystyle 2\pi i.}$

Si es un número racional con m y n enteros coprimos con entonces tiene exactamente n valores. En el caso de que estos valores sean los mismos que los descritos en § Raíces n-ésimas de un número complejo. Si w es un entero, solo hay un valor que concuerda con el de § Exponentes enteros.${\displaystyle w={\frac {m}{n}}}$ ${\displaystyle n>0,}$${\displaystyle z^{w}}$${\displaystyle m=1,}$

La exponenciación multivaluada es holomorfa en el sentido de que su gráfica consta de varias láminas que definen cada una una función holomorfa en la vecindad de cada punto. Si z varía continuamente a lo largo de un círculo alrededor de 0 , entonces, después de un giro, el valor de ha cambiado de lámina.${\displaystyle z\neq 0,}$${\displaystyle z^{w}}$

La forma canónica de se puede calcular a partir de la forma canónica de z y w . Aunque esto se puede describir con una única fórmula, resulta más claro dividir el cálculo en varios pasos.${\displaystyle x+iy}$${\displaystyle z^{w}}$

• Forma polar de z . Sies la forma canónica de z ( a y b son reales), entonces su forma polar esdondey(consulte atan2 para la definición de esta función).${\displaystyle z=a+ib}$$${\displaystyle z=\rho e^{i\theta }=\rho (\cos \theta +i\sin \theta ),}$$${\displaystyle \rho ={\sqrt {a^{2}+b^{2}}}}$${\displaystyle \theta =\operatorname {atan2} (a,b)}$
• Logaritmo de z . El valor principal de este logaritmo esdondedenota el logaritmo natural . Los demás valores del logaritmo se obtienen sumandopara cualquier entero k .${\displaystyle \log z=\ln \rho +i\theta ,}$${\displaystyle \ln }$${\displaystyle 2ik\pi }$
• Forma canónica de${\displaystyle w\log z.}$ Si con c y d reales, los valores de son el valor principal correspondiente a${\displaystyle w=c+di}$${\displaystyle w\log z}$$${\displaystyle w\log z=(c\ln \rho -d\theta -2dk\pi )+i(d\ln \rho +c\theta +2ck\pi ),}$$${\displaystyle k=0.}$
• Resultado final . Utilizando las identidades y se obtiene con para el valor principal.${\displaystyle e^{x+y}=e^{x}e^{y}}$${\displaystyle e^{y\ln x}=x^{y},}$$${\displaystyle z^{w}=\rho ^{c}e^{-d(\theta +2k\pi )}\left(\cos(d\ln \rho +c\theta +2ck\pi )+i\sin(d\ln \rho +c\theta +2ck\pi )\right),}$$${\displaystyle k=0}$

• ${\displaystyle i^{i}}$
  La forma polar de i es y los valores de son, por lo tanto, se deduce que Entonces, todos los valores de son reales, siendo el principal${\displaystyle i=e^{i\pi /2},}$${\displaystyle \log i}$$${\displaystyle \log i=i\left({\frac {\pi }{2}}+2k\pi \right).}$$$${\displaystyle i^{i}=e^{i\log i}=e^{-{\frac {\pi }{2}}}e^{-2k\pi }.}$$${\displaystyle i^{i}}$$${\displaystyle e^{-{\frac {\pi }{2}}}\approx 0.2079.}$$
• ${\displaystyle (-2)^{3+4i}}$
  De manera similar, la forma polar de −2 es Entonces, el método descrito anteriormente proporciona los valores En este caso, todos los valores tienen el mismo argumento y diferentes valores absolutos.${\displaystyle -2=2e^{i\pi }.}$$${\displaystyle {\begin{aligned}(-2)^{3+4i}&=2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2+3(\pi +2k\pi ))+i\sin(4\ln 2+3(\pi +2k\pi )))\\&=-2^{3}e^{-4(\pi +2k\pi )}(\cos(4\ln 2)+i\sin(4\ln 2)).\end{aligned}}}$$${\displaystyle 4\ln 2,}$

En ambos ejemplos, todos los valores de tienen el mismo argumento. En términos más generales, esto es cierto si y solo si la parte real de w es un número entero.${\displaystyle z^{w}}$

Algunas identidades para potencias y logaritmos de números reales positivos fallarán para números complejos, sin importar cuán complejas sean las potencias y logaritmos complejos definidos como funciones de un solo valor . Por ejemplo:

Si b es un número algebraico real positivo y x es un número racional, entonces b ^x es un número algebraico. Esto resulta de la teoría de extensiones algebraicas . Esto sigue siendo cierto si b es cualquier número algebraico, en cuyo caso, todos los valores de b ^x (como una función multivaluada ) son algebraicos. Si x es irracional (es decir, no racional ), y tanto b como x son algebraicos, el teorema de Gelfond-Schneider afirma que todos los valores de b ^x son trascendentales (es decir, no algebraicos), excepto si b es igual a 0 o 1 .

En otras palabras, si x es irracional y entonces al menos uno de b , x y b ^x es trascendental.${\displaystyle b\not \in \{0,1\},}$

La definición de exponenciación con exponentes enteros positivos como multiplicación repetida puede aplicarse a cualquier operación asociativa denotada como una multiplicación. ^{[nb 2]} La definición de x ⁰ requiere además la existencia de una identidad multiplicativa . ^[33]

Una estructura algebraica que consiste en un conjunto junto con una operación asociativa denotada multiplicativamente y una identidad multiplicativa denotada por 1 es un monoide . En tal monoide, la exponenciación de un elemento x se define inductivamente por

• ${\displaystyle x^{0}=1,}$
• ${\displaystyle x^{n+1}=xx^{n}}$para cada entero no negativo n .

Si n es un entero negativo, se define solo si x tiene un inverso multiplicativo . ^[34] En este caso, el inverso de x se denota x ⁻¹ , y x ⁿ se define como${\displaystyle x^{n}}$${\displaystyle \left(x^{-1}\right)^{-n}.}$

La exponenciación con exponentes enteros obedece las siguientes leyes, para x e y en la estructura algebraica, y m y n números enteros:

${\displaystyle {\begin{aligned}x^{0}&=1\\x^{m+n}&=x^{m}x^{n}\\(x^{m})^{n}&=x^{mn}\\(xy)^{n}&=x^{n}y^{n}\quad {\text{if }}xy=yx,{\text{and, in particular, if the multiplication is commutative.}}\end{aligned}}}$

Estas definiciones se utilizan ampliamente en muchas áreas de las matemáticas, en particular para grupos , anillos , cuerpos y matrices cuadradas (que forman un anillo). También se aplican a funciones de un conjunto a sí mismo, que forman un monoide bajo composición de funciones . Esto incluye, como casos específicos, las transformaciones geométricas y los endomorfismos de cualquier estructura matemática .

Cuando existen varias operaciones que pueden repetirse, es común indicar la operación repetida colocando su símbolo en el superíndice, antes del exponente. Por ejemplo, si f es una función real cuyo valor puede ser multiplicado, denota la potenciación respecto de la multiplicación, y puede denotar la potenciación respecto de la composición de la función . Es decir,${\displaystyle f^{n}}$${\displaystyle f^{\circ n}}$

${\displaystyle (f^{n})(x)=(f(x))^{n}=f(x)\,f(x)\cdots f(x),}$

y

${\displaystyle (f^{\circ n})(x)=f(f(\cdots f(f(x))\cdots )).}$

Comúnmente, se denota mientras que se denota${\displaystyle (f^{n})(x)}$${\displaystyle f(x)^{n},}$${\displaystyle (f^{\circ n})(x)}$${\displaystyle f^{n}(x).}$

Un grupo multiplicativo es un conjunto con una operación asociativa denotada como multiplicación, que tiene un elemento identidad y tal que cada elemento tiene un inverso.

Entonces, si G es un grupo, se define para todo y cada entero n .${\displaystyle x^{n}}$${\displaystyle x\in G}$

El conjunto de todas las potencias de un elemento de un grupo forma un subgrupo . Un grupo (o subgrupo) que consta de todas las potencias de un elemento específico x es el grupo cíclico generado por x . Si todas las potencias de x son distintas, el grupo es isomorfo al grupo aditivo de los números enteros. En caso contrario, el grupo cíclico es finito (tiene un número finito de elementos), y su número de elementos es el orden de x . Si el orden de x es n , entonces y el grupo cíclico generado por x consta de las n primeras potencias de x (empezando indistintamente por el exponente 0 o 1 ).${\displaystyle \mathbb {Z} }$${\displaystyle x^{n}=x^{0}=1,}$

El orden de los elementos juega un papel fundamental en la teoría de grupos . Por ejemplo, el orden de un elemento en un grupo finito es siempre un divisor del número de elementos del grupo (el orden del grupo). Los posibles órdenes de los elementos del grupo son importantes en el estudio de la estructura de un grupo (ver teoremas de Sylow ) y en la clasificación de grupos finitos simples .

La notación superíndice también se utiliza para la conjugación ; es decir, g ^h = h ⁻¹ gh , donde g y h son elementos de un grupo. Esta notación no se puede confundir con la exponenciación, ya que el superíndice no es un número entero. La motivación de esta notación es que la conjugación obedece algunas de las leyes de la exponenciación, a saber :${\displaystyle (g^{h})^{k}=g^{hk}}$${\displaystyle (gh)^{k}=g^{k}h^{k}.}$

En un anillo , puede ocurrir que algunos elementos distintos de cero satisfagan para algún entero n . Se dice que un elemento de este tipo es nilpotente . En un anillo conmutativo , los elementos nilpotentes forman un ideal , llamado el radical nil del anillo.${\displaystyle x^{n}=0}$

Si el radical nil se reduce al ideal cero (es decir, si implica para cada entero positivo n ), se dice que el anillo conmutativo está reducido . Los anillos reducidos son importantes en geometría algebraica , ya que el anillo de coordenadas de un conjunto algebraico afín es siempre un anillo reducido.${\displaystyle x\neq 0}$${\displaystyle x^{n}\neq 0}$

En términos más generales, dado un ideal I en un anillo conmutativo R , el conjunto de los elementos de R que tienen una potencia en I es un ideal, llamado radical de I . El nilradical es el radical del ideal cero . Un ideal radical es un ideal que es igual a su propio radical. En un anillo de polinomios sobre un cuerpo k , un ideal es radical si y solo si es el conjunto de todos los polinomios que son cero en un conjunto algebraico afín (esto es una consecuencia del Nullstellensatz de Hilbert ).${\displaystyle k[x_{1},\ldots ,x_{n}]}$

Si A es una matriz cuadrada, entonces el producto de A consigo misma n veces se denomina potencia de matriz . También se define como la matriz identidad, ^[35] y si A es invertible, entonces .${\displaystyle A^{0}}$${\displaystyle A^{-n}=\left(A^{-1}\right)^{n}}$

Las potencias matriciales aparecen a menudo en el contexto de sistemas dinámicos discretos , donde la matriz A expresa una transición desde un vector de estado x de algún sistema al siguiente estado Ax del sistema. ^[36] Esta es la interpretación estándar de una cadena de Markov , por ejemplo. Entonces es el estado del sistema después de dos pasos de tiempo, y así sucesivamente: es el estado del sistema después de n pasos de tiempo. La potencia matricial es la matriz de transición entre el estado actual y el estado en un momento n pasos en el futuro. Por lo tanto, calcular potencias matriciales es equivalente a resolver la evolución del sistema dinámico. En muchos casos, las potencias matriciales se pueden calcular convenientemente utilizando valores propios y vectores propios .${\displaystyle A^{2}x}$${\displaystyle A^{n}x}$${\displaystyle A^{n}}$

Además de las matrices, también se pueden exponenciar operadores lineales más generales. Un ejemplo es el operador de derivada del cálculo, , que es un operador lineal que actúa sobre funciones para dar una nueva función . La potencia n del operador de diferenciación es la derivada n :${\displaystyle d/dx}$${\displaystyle f(x)}$${\displaystyle (d/dx)f(x)=f'(x)}$

${\displaystyle \left({\frac {d}{dx}}\right)^{n}f(x)={\frac {d^{n}}{dx^{n}}}f(x)=f^{(n)}(x).}$

Estos ejemplos son para exponentes discretos de operadores lineales, pero en muchas circunstancias también es deseable definir potencias de tales operadores con exponentes continuos. Este es el punto de partida de la teoría matemática de semigrupos . ^[37] Así como el cálculo de potencias matriciales con exponentes discretos resuelve sistemas dinámicos discretos, el cálculo de potencias matriciales con exponentes continuos resuelve sistemas con dinámica continua. Los ejemplos incluyen enfoques para resolver la ecuación del calor , la ecuación de Schrödinger , la ecuación de onda y otras ecuaciones diferenciales parciales que incluyen una evolución temporal. El caso especial de exponenciar el operador derivada a una potencia no entera se llama derivada fraccionaria que, junto con la integral fraccionaria , es una de las operaciones básicas del cálculo fraccionario .

Un campo es una estructura algebraica en la que se definen la multiplicación, la suma, la resta y la división y satisfacen las propiedades de que la multiplicación es asociativa y cada elemento distinto de cero tiene un inverso multiplicativo . Esto implica que la exponenciación con exponentes enteros está bien definida, excepto para potencias no positivas de 0. Ejemplos comunes son el campo de números complejos , los números reales y los números racionales , considerados anteriormente en este artículo, que son todos infinitos .

Un cuerpo finito es un cuerpo con un número finito de elementos. Este número de elementos es un número primo o una potencia prima ; es decir, tiene la forma donde p es un número primo y k es un entero positivo. Para cada q de este tipo , existen cuerpos con q elementos. Los cuerpos con q elementos son todos isomorfos , lo que permite, en general, trabajar como si hubiera un solo cuerpo con q elementos, denotado${\displaystyle q=p^{k},}$${\displaystyle \mathbb {F} _{q}.}$

Uno tiene

${\displaystyle x^{q}=x}$

Para cada uno${\displaystyle x\in \mathbb {F} _{q}.}$

Un elemento primitivo en es un elemento g tal que el conjunto de las q − 1 primeras potencias de g (es decir, ) es igual al conjunto de los elementos distintos de cero de Hay elementos primitivos en donde es la función totiente de Euler .${\displaystyle \mathbb {F} _{q}}$${\displaystyle \{g^{1}=g,g^{2},\ldots ,g^{p-1}=g^{0}=1\}}$${\displaystyle \mathbb {F} _{q}.}$${\displaystyle \varphi (p-1)}$${\displaystyle \mathbb {F} _{q},}$${\displaystyle \varphi }$