Enlace de Chebyshev

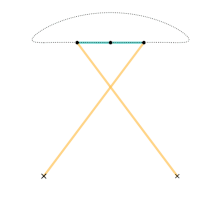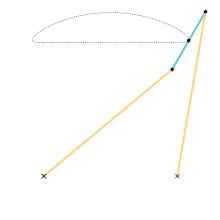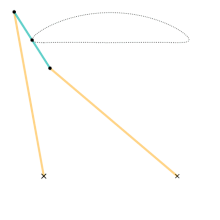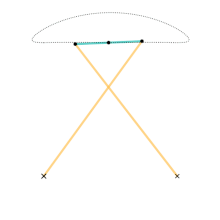
En cinemática , el mecanismo de Chebyshev es un mecanismo de cuatro barras que convierte el movimiento rotacional en un movimiento lineal aproximado .

Fue inventado por el matemático del siglo XIX Pafnuty Chebyshev , quien estudió problemas teóricos en mecanismos cinemáticos . Uno de los problemas era la construcción de un mecanismo que convierte un movimiento rotatorio en un movimiento aproximado en línea recta (un mecanismo de línea recta ). Esto también fue estudiado por James Watt en sus mejoras a la máquina de vapor , que dieron como resultado el mecanismo de Watt . ^[1]

El movimiento del eslabón puede limitarse a un ángulo de entrada que puede modificarse mediante velocidades, fuerzas, etc. Los ángulos de entrada pueden ser el eslabón  L ₂ con la horizontal o el eslabón  L ₄ con la horizontal. Independientemente del ángulo de entrada, es posible calcular el movimiento de dos puntos finales del eslabón  L ₃ que llamaremos A y B, y el punto medio.

${\ Displaystyle x_ {A} = L_ {2} \ cos (\ varphi _ {1}) \,}$

${\ Displaystyle y_ {A} = L_ {2} \ sin (\ varphi _ {1}) \,}$

mientras que el movimiento del punto B se calculará con el otro ángulo,

${\ Displaystyle x_ {B} = L_ {1} -L_ {4} \ cos (\ varphi _ {2}) \,}$

${\ Displaystyle y_ {B} = L_ {4} \ sin (\ varphi _ {2}) \,}$

Y finalmente, escribiremos el ángulo de salida en términos del ángulo de entrada,

${\displaystyle \varphi _{2}=\arcsin \left[{\frac {L_{2}\,\sin(\varphi _{1})}{\overline {AO_{2}}}}\right] -\arccos \left({\frac {L_{4}^{2}+{\overline {AO_{2}}}^{2}-L_{3}^{2}}{2\,L_{4 }\,{\overline {AO_{2}}}}}\right)\,}$

En consecuencia, podemos escribir el movimiento del punto P, utilizando los dos puntos definidos anteriormente y la definición del punto medio.

${\displaystyle x_{P}={\frac {x_{A}+x_{B}}{2}}\,}$

${\displaystyle y_{P}={\frac {y_{A}+y_{B}}{2}}\,}$

Los límites de los ángulos de entrada, en ambos casos, son:

${\displaystyle \varphi _{\text{min}}=\arccos \left({\frac {4}{5}}\right)\aproximadamente 36,8699^{\circ }.\,}$

${\displaystyle \varphi _{\text{máx}}=\arccos \izquierda({\frac {-1}{5}}\derecha)\aproximadamente 101,537^{\circ }.\,}$

Los mecanismos de Chebyshev no se utilizaron ampliamente en las máquinas de vapor, ^{[ cita requerida ]} pero se utilizan comúnmente como el diseño de "cabeza de caballo" de la grúa de elevación horizontal . En esta aplicación, el movimiento recto aproximado se traslada desde el punto medio de la línea, pero sigue siendo esencialmente el mismo mecanismo.

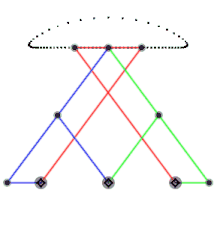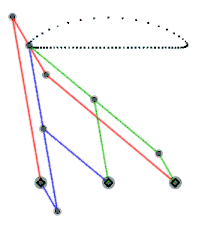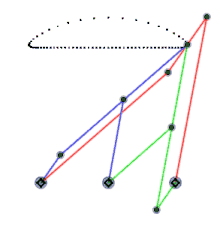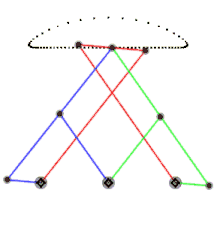
• Enlace lambda de Chebyshev , cognado del enlace de Chebyshev.
• Enlace de cuatro barras
• Mecanismo de línea recta

Wikimedia Commons alberga una categoría multimedia sobre Vínculo de Chebyshev .

• Universidad de Cornell, "Cómo dibujar una línea recta", por AB Kempe, BA
• Una simulación archivada el 25 de julio de 2011 en Wayback Machine utilizando el software Molecular Workbench
• Una simulación de Geogebra del vínculo
• Un vídeo en 3D del enlace.