Números griegos
La introducción de este artículo puede ser demasiado breve para resumir adecuadamente los puntos clave . ( Marzo de 2024 ) |
| Parte de una serie sobre |
| Sistemas de numeración |
|---|
| List of numeral systems |
Los números griegos , también conocidos como numerales jónicos , jónicos , milesios o alejandrinos , son un sistema de escritura de números que utiliza las letras del alfabeto griego . En la Grecia moderna , todavía se utilizan para números ordinales y en contextos similares a aquellos en los que todavía se utilizan los números romanos en el mundo occidental . Sin embargo, para los números cardinales ordinarios , la Grecia moderna utiliza números arábigos .
Historia
Los alfabetos lineal A y lineal B de las civilizaciones minoica y micénica usaban un sistema diferente, llamado numerales egeos , que incluía símbolos exclusivamente numéricos para potencias de diez: 𐄇 = 1, 𐄐 = 10, 𐄙 = 100, 𐄢 = 1000 y 𐄫 = 10000. [1]
Los numerales áticos componían otro sistema que entró en uso quizás en el siglo VII a. C. Eran acrofónicos , derivados (después de la inicial) de las primeras letras de los nombres de los números representados.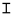 = 1,
= 1, = 5,
= 5,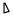 = 10,
= 10, = 100,
= 100,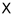 = 1.000, y
= 1.000, y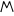 = 10,000. Los números 50, 500, 5,000 y 50,000 fueron representados por la letra
= 10,000. Los números 50, 500, 5,000 y 50,000 fueron representados por la letra con minúsculas potencias de diez escritas en la esquina superior derecha:
con minúsculas potencias de diez escritas en la esquina superior derecha: ,
, ,
,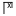 , y
, y . [1] La mitad se representaba con 𐅁 (la mitad izquierda de un círculo completo) y un cuarto con ɔ (el lado derecho de un círculo completo). El mismo sistema se utilizaba fuera del Ática , pero los símbolos variaban con los alfabetos locales ; por ejemplo, 1000 era
. [1] La mitad se representaba con 𐅁 (la mitad izquierda de un círculo completo) y un cuarto con ɔ (el lado derecho de un círculo completo). El mismo sistema se utilizaba fuera del Ática , pero los símbolos variaban con los alfabetos locales ; por ejemplo, 1000 era en Beocia . [2]
en Beocia . [2]
El sistema actual probablemente se desarrolló alrededor de Mileto en Jonia . Los clasicistas del siglo XIX situaron su desarrollo en el siglo III a. C., ocasión de su primer uso generalizado. [3] La arqueología moderna más exhaustiva ha hecho que la fecha se retrase al menos al siglo V a. C., [4] un poco antes de que Atenas abandonara su alfabeto preeucleideo en favor del de Mileto en 402 a. C., y puede ser anterior a eso por un siglo o dos. [5] El sistema actual utiliza las 24 letras adoptadas bajo Eucleides , así como tres fenicias y jónicas que no habían sido eliminadas del alfabeto ateniense (aunque se mantuvieron para números): digamma , koppa y sampi . La posición de esos caracteres dentro del sistema de numeración implica que los dos primeros todavía estaban en uso (o al menos se recordaban como letras) mientras que el tercero no. La datación exacta, en particular para sampi , es problemática ya que su valor poco común significa que el primer representante atestiguado cerca de Mileto no aparece hasta el siglo II a. C., [6] y su uso no está atestiguado en Atenas hasta el siglo II d. C. [7] (En general, los atenienses se resistieron a usar los nuevos numerales durante más tiempo que cualquier otro estado griego, pero los adoptaron por completo alrededor del año 50 d . C. [2] ).
Descripción

Los números griegos son decimales , basados en potencias de 10. Las unidades del 1 al 9 se asignan a las primeras nueve letras del antiguo alfabeto jónico, desde alfa hasta theta . Sin embargo, en lugar de reutilizar estos números para formar múltiplos de las potencias superiores de diez, a cada múltiplo de diez del 10 al 90 se le asignó su propia letra separada de las siguientes nueve letras del alfabeto jónico, desde iota hasta koppa . A cada múltiplo de cien del 100 al 900 también se le asignó su propia letra separada, desde rho hasta sampi . [8] (El hecho de que esta no fuera la ubicación tradicional de sampi en el orden alfabético jónico ha llevado a los clasicistas a concluir que sampi había caído en desuso como letra cuando se creó el sistema. [ cita requerida ] )
Este sistema alfabético funciona según el principio aditivo, en el que los valores numéricos de las letras se suman para obtener el total. Por ejemplo, 241 se representaba como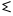
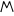
 (200 + 40 + 1). (No siempre fue el caso de que los números fueran de mayor a menor: una inscripción del siglo IV a. C. en Atenas colocó las unidades a la izquierda de las decenas. Esta práctica continuó en Asia Menor hasta bien entrado el período romano . [9] ) En los manuscritos antiguos y medievales, estos numerales finalmente se distinguieron de las letras usando barras superpuestas : α , β , γ , etc. En los manuscritos medievales del Libro de Apocalipsis , el número de la Bestia 666 se escribe como χξϛ (600 + 60 + 6). (Los números mayores de 1000 reutilizaban las mismas letras pero incluían varias marcas para notar el cambio). Las fracciones se indicaban como el denominador seguido de una keraia (ʹ); γʹ indicaba un tercio, δʹ un cuarto y así sucesivamente. Como excepción, el símbolo especial ∠ʹ indicaba la mitad, y γ°ʹ o γoʹ eran dos tercios. Estas fracciones eran aditivas (también conocidas como fracciones egipcias ); por ejemplo, δʹ ϛʹ indicaba 1 ⁄ 4 + 1 ⁄ 6 = 5 ⁄ 12 .
(200 + 40 + 1). (No siempre fue el caso de que los números fueran de mayor a menor: una inscripción del siglo IV a. C. en Atenas colocó las unidades a la izquierda de las decenas. Esta práctica continuó en Asia Menor hasta bien entrado el período romano . [9] ) En los manuscritos antiguos y medievales, estos numerales finalmente se distinguieron de las letras usando barras superpuestas : α , β , γ , etc. En los manuscritos medievales del Libro de Apocalipsis , el número de la Bestia 666 se escribe como χξϛ (600 + 60 + 6). (Los números mayores de 1000 reutilizaban las mismas letras pero incluían varias marcas para notar el cambio). Las fracciones se indicaban como el denominador seguido de una keraia (ʹ); γʹ indicaba un tercio, δʹ un cuarto y así sucesivamente. Como excepción, el símbolo especial ∠ʹ indicaba la mitad, y γ°ʹ o γoʹ eran dos tercios. Estas fracciones eran aditivas (también conocidas como fracciones egipcias ); por ejemplo, δʹ ϛʹ indicaba 1 ⁄ 4 + 1 ⁄ 6 = 5 ⁄ 12 .
Aunque el alfabeto griego comenzó con sólo formas mayúsculas , los manuscritos de papiro que sobrevivieron de Egipto muestran que las formas unciales y cursivas minúsculas comenzaron temprano. [ aclaración necesaria ] Estas nuevas formas de letras a veces reemplazaron a las anteriores, especialmente en el caso de los oscuros numerales. La antigua koppa en forma de Q (Ϙ) comenzó a fragmentarse ( y
y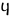 ) y simplificado (
) y simplificado ( y
y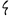 ). El número 6 cambió varias veces. Durante la antigüedad, se dejó de lado la forma original de la letra digamma (Ϝ) en favor de una forma numérica especial (
). El número 6 cambió varias veces. Durante la antigüedad, se dejó de lado la forma original de la letra digamma (Ϝ) en favor de una forma numérica especial ( ). En la época bizantina , la carta se conocía como episemon y se escribía como
). En la época bizantina , la carta se conocía como episemon y se escribía como o
o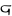 . Esto finalmente se fusionó con el estigma de la ligadura sigma - tau ϛ (
. Esto finalmente se fusionó con el estigma de la ligadura sigma - tau ϛ (  o
o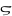 ).
).
En el griego moderno se han realizado otros cambios. En lugar de extender una barra sobre un número entero, la keraia ( κεραία , lit. "proyección en forma de cuerno") se marca en la parte superior derecha, un desarrollo de las marcas cortas que se usaban anteriormente para números simples y fracciones. La keraia moderna (´) es un símbolo similar al acento agudo (´), los tonos (U+0384,΄) y el símbolo de prima (U+02B9, ʹ), pero tiene su propio carácter Unicode como U+0374. El padre de Alejandro Magno, Filipo II de Macedonia , es conocido como Φίλιππος Βʹ en griego moderno. Un keraia inferior izquierdo (Unicode: U+0375, "signo numérico inferior griego") es ahora el estándar para distinguir miles: 2019 se representa como ͵ΒΙΘʹ ( 2 × 1.000 + 10 + 9 ).
El uso decreciente de ligaduras en el siglo XX también significa que el estigma se escribe frecuentemente con las letras separadas ΣΤʹ, aunque se utiliza una única keraia para el grupo. [10]
Isopsefia
La práctica de sumar los valores numéricos de las letras griegas de palabras, nombres y frases, conectando así el significado de palabras, nombres y frases con otros con sumas numéricas equivalentes, se llama isopsefia . Prácticas similares para el hebreo y el inglés se llaman gematría y Qaballa inglesa , respectivamente.
Mesa
| Antiguo | bizantino | Moderno | Valor | Antiguo | bizantino | Moderno | Valor | Antiguo | bizantino | Moderno | Valor | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
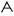 | α̅ | Aʹ | 1 |  | yo | Yo | 10 | 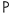 | ρ̅ | P' | 100 | ||
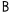 | β | B' | 2 | 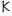 | k | K' | 20 | 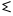 | σ̅ | Σʹ | 200 | ||
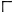 | γ̅ | Γʹ | 3 | 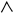 | λ̅ | La | 30 | 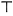 | τ̅ | T | 300 | ||
 | δ̅ | Δʹ | 4 | 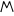 | μ̅ | mi | 40 | 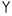 | υ̅ | Υʹ | 400 | ||
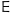 | ε̅ | Yo | 5 |  | n | No | 50 |  | φ̅ | Φʹ | 500 | ||
  |  y y 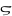 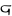 y y  | Ϛʹ Ϝʹ ΣΤʹ | 6 |  | ξ̅ | Oh | 60 | 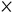 | χ̅ | Χʹ | 600 | ||
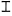 | ζ̅ | Oh | 7 | 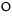 | o̅ | Oh | 70 |  | ψ̅ | Ψʹ | 700 | ||
 | η̅ | Oh | 8 | 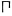 | π̅ | P' | 80 |  | ω̅ | Ωʹ | 800 | ||
 | θ̅ | Θʹ | 9 |   |  y y  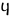 y y 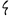 | Ϟʹ Ϙʹ | 90 | 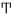  y y 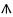  y y  |  y y  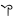  y y 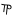 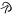 y y   | Ϡʹ Ͳʹ | 900 | ||
 y y  | ͵α | ,A | 1000 |   | ͵ι | ,yo | 10000 |   | ͵ρ | ,P | 100000 | ||
  | ͵β | ,B | 2000 |   | ͵κ | ,K | 20000 |   | ͵σ | ,Σ | 200000 | ||
  | ͵ | ,Γ | 3000 |   | ͵λ | ,Λ | 30000 |   | ͵τ | ,T | 300000 | ||
  | ͵ | ,Δ | 4000 |   | ͵μ | ,M | 40000 |   | ͵υ | ,Υ | 400000 | ||
  | ͵ε | ,E | 5000 |   | ͵ν | ,N | 50000 |   | ͵φ | ,Φ | 500000 | ||
    | ͵ y ͵ y ͵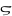 ͵ 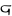 y ͵ y ͵ | ,Ϛ ,Ϝ ,ΣΤ | 6000 |   | ͵ξ | ,O | 60000 |   | ͵χ | ,Χ | 600000 | ||
  | ͵ζ | ,O | 7000 |   | ͵ο | ,O | 70000 |   | ͵ψ | ,Ψ | 700000 | ||
  | ͵η | ,H | 8000 |   | ͵π | ,Π | 80000 |   | ͵ω | ,Ω | 800000 | ||
 | ͵θ | ,Θ | 9000 |     | ͵ y ͵ y ͵ ͵ 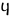 y ͵ y ͵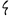 | ,Ϟ ,Ϙ | 90000 |     y y     y y   | ͵ y ͵ y ͵ ͵ 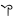 ͵  y ͵ y ͵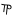 ͵ 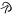 y ͵ y ͵ ͵  | ,Ϡ ,Ͳ | 900000 |
- Alternativamente, las subsecciones de los manuscritos a veces se numeran con caracteres minúsculos (αʹ, βʹ, γʹ, δʹ, εʹ, ϛʹ, ζʹ, ηʹ, θʹ).
- En griego antiguo, se utiliza la notación miríada para múltiplos de 10 000, por ejemploβmipor 20.000 oρκγmi͵δφξζ (también escrito en la línea como ρκγ Μ ͵δφξζ ) por 1.234.567. [11]
Números más altos
En su texto El contador de arena , el filósofo natural Arquímedes establece un límite superior para la cantidad de granos de arena necesarios para llenar todo el universo, utilizando una estimación contemporánea de su tamaño. Esto desafiaría la idea, entonces sostenida, de que es imposible nombrar un número mayor que el de la arena de una playa o del mundo entero. Para ello, tuvo que idear un nuevo esquema numérico con un alcance mucho mayor.
Pappus de Alejandría informa que Apolonio de Perge desarrolló un sistema más simple basado en poderes de la miríada;alfamiEran 10.000,βmiera 10.000 2 = 100.000.000,gammamiera 10.000 3 = 10 12 y así sucesivamente. [11]
Cero

Los astrónomos helenísticos extendieron los numerales alfabéticos griegos a un sistema de numeración posicional sexagesimal al limitar cada posición a un valor máximo de 50 + 9 e incluir un símbolo especial para el cero , que solo se usaba solo para una celda completa de la tabla, en lugar de combinarse con otros dígitos, como el cero moderno actual, que es un marcador de posición en la notación numérica posicional. Este sistema probablemente fue adaptado de los numerales babilónicos por Hiparco c. 140 a. C. Luego fue utilizado por Ptolomeo ( c. 140 a. C. ), Teón ( c. 380 d. C. ) y la hija de Teón, Hipatia ( m. 415 d. C. ). El símbolo del cero es claramente diferente del del valor de 70, ómicrón u " ο ". En el papiro del siglo II que se muestra aquí, se puede ver el símbolo del cero en la parte inferior derecha y una serie de ómicrones más grandes en otras partes del mismo papiro.
En la tabla de cuerdas de Ptolomeo , la primera tabla trigonométrica bastante extensa, había 360 filas, partes de las cuales tenían el siguiente aspecto:
Cada número de la primera columna, denominada περιφερειῶν , ["regiones"] es el número de grados de arco de un círculo. Cada número de la segunda columna, denominada εὐθειῶν , ["líneas rectas" o "segmentos"] es la longitud de la cuerda correspondiente del círculo, cuando el diámetro es 120. Por lo tanto, πδ representa un arco de 84°, y el ∠′ después de él significa la mitad, de modo que πδ∠′ significa 84+1⁄2 ° . En la siguiente columna vemos π μα γ , que significa 80 + 41/60 + 3/60² . Esa es la longitud de la cuerda correspondiente a un arco de 84+1 ⁄ 2 ° cuando el diámetro del círculo es 120. La siguiente columna, denominada ἐξηκοστῶν , que significa "sesentavo", es el número que se debe agregar a la longitud de la cuerda por cada aumento de 1° en el arco, durante el lapso de los siguientes 12°. Por lo tanto, esa última columna se utilizó para la interpolación lineal .
El símbolo griego del cero o del sexagesimal cambió con el tiempo: el símbolo utilizado en los papiros durante el siglo II era un círculo muy pequeño con una barra de varios diámetros de largo, terminada o no en ambos extremos de diversas maneras. Más tarde, la barra se acortó a un solo diámetro, similar al o -macron (ō) moderno que todavía se usaba en los manuscritos árabes de finales de la Edad Media siempre que se usaban numerales alfabéticos, más tarde la barra se omitió en los manuscritos bizantinos , dejando un ο (ómicron) desnudo. [12] [13] Este cambio gradual de un símbolo inventado a ο no respalda la hipótesis de que este último fuera la inicial de οὐδέν que significa "nada". [14] [15] Nótese que la letra ο todavía se usaba con su valor numérico original de 70; sin embargo, no había ambigüedad, ya que 70 no podía aparecer en la parte fraccionaria de un número sexagesimal , y el cero generalmente se omitía cuando era el entero.
Algunos de los ceros verdaderos de Ptolomeo aparecían en la primera línea de cada una de sus tablas de eclipses, donde eran una medida de la separación angular entre el centro de la Luna y el centro del Sol (para los eclipses solares ) o el centro de la sombra de la Tierra (para los eclipses lunares ). Todos estos ceros tomaron la forma ο | ο ο , donde Ptolomeo en realidad utilizó tres de los símbolos descritos en el párrafo anterior. La barra vertical (|) indica que la parte integral de la izquierda estaba en una columna separada etiquetada en los encabezados de sus tablas como dígitos (de cinco minutos de arco cada uno), mientras que la parte fraccionaria estaba en la siguiente columna etiquetada minuto de inmersión , es decir, sexagésimos (y treinta y seis centésimas) de un dígito. [16]
| Avance | 𐆊 | |
|---|---|---|
| Nombre Unicode | SIGNO CERO GRIEGO | |
| Codificaciones | decimal | maleficio |
| Unicode | 65930 | U+1018A |
| UTF-8 | 240 144 134 138 | F090868A |
| UTF-16 | 55296 56714 | D800 DD8A |
| Referencia de caracteres numéricos | - | " |
Véase también
- Sistema de numeración alfabético – Tipo de sistema de numeración
- Números áticos : notación numérica simbólica utilizada por los antiguos griegos
- Números cirílicos : sistema de numeración derivado de la escritura cirílica
- Matemáticas griegas – Matemáticas de los antiguos griegos
- Numerales griegos en Unicode : grafemas para varios sistemas numéricos Pages displaying short descriptions of redirect targets(numerales acrofónicos, no alfabéticos)
- Numeración hebrea : sistema de numeración que utiliza letras del alfabeto hebreo, basado en el sistema griego.
- Historia de los sistemas de numeración antiguos – Símbolos que representan números
- Historia de la aritmética – Rama de las matemáticas elementalesPages displaying short descriptions of redirect targets
- Historia de la comunicación
- Isopsefia – Conexión numerológica entre palabras cuyos valores numéricos de letras tienen sumas iguales
- Lista de temas del sistema de numeración
- Lista de sistemas de numeración
- Número de la bestia – Número asociado con la Bestia del Apocalipsis
- Números romanos – Números en el sistema de numeración romana
Referencias
- ^ ab Verdan, Samuel (20 de marzo de 2007). "Systèmes numéraux en Grèce ancienne: Descripción et mise en outlook historique" (en francés). Archivado desde el original el 2 de febrero de 2010 . Consultado el 2 de marzo de 2011 .
- ^ ab Heath, Thomas L. (2003) [1931]. Un manual de matemáticas griegas ( [2003] reimpresión ed.). Oxford, Reino Unido: Oxford University Press [1931] ; Dover Books [2003] . pp. 14 y siguientes. ISBN 9780486154442. Recuperado el 1 de noviembre de 2013 – vía Google Books.
- ^ Thompson, Edward M. (1893). Manual de paleografía griega y latina . Nueva York, NY: D. Appleton. pág. 114.
- ^ "IG I³ 1387". Inscripciones griegas que se pueden buscar . The Packard Humanities Institute. Cornell University & Ohio State University . IG I³ 1387 también conocida como IG I² 760. Consultado el 1 de noviembre de 2013 .
- ^ Jeffery, Lilian H. (1961). Las escrituras locales de la Grecia arcaica . Oxford, Reino Unido: Clarendon Press. pp. 38 y siguientes.
- ^ "Magnesia 4". Inscripciones griegas que se pueden buscar . The Packard Humanities Institute. Cornell University & Ohio State University . Magnesia 4 también conocida como Syll³ 695.b. Consultado el 1 de noviembre de 2013 .
- ^ "IG II² 2776". Inscripciones griegas que se pueden buscar . The Packard Humanities Institute. Cornell University & Ohio State University . Consultado el 1 de noviembre de 2013 .
- ^ Edkins, Jo (2006). «Números griegos clásicos». Archivado desde el original el 10 de mayo de 2013. Consultado el 29 de abril de 2013 .
- ^ Heath, Thomas L. A Manual of Greek Mathematics , págs. 14 y siguientes. Oxford Univ. Press (Oxford), 1931. Reimpreso en Dover ( Mineola ), 2003. Consultado el 1 de noviembre de 2013.
- ^ Nick Nicholas (9 de abril de 2005). «Números: Stigma, Koppa, Sampi». Archivado desde el original el 5 de agosto de 2012. Consultado el 2 de marzo de 2011 .
- ^ ab Sistemas de numeración griegos - MacTutor
- ^ https://www.unicode.org/L2/L2004/04054-greek-zero.pdf [ URL básica PDF ]
- ^ https://raymondm.co.uk/prog/GreekZeroSign.pdf [ URL básica PDF ]
- ^ Neugebauer, Otto (1969) [1957]. Las ciencias exactas en la antigüedad (2.ª edición, reimpresión). Dover Publications , págs. 13-14, lámina 2. ISBN 978-0-486-22332-2.
- ^ Mercier, Raymond. "Consideración del símbolo griego 'cero'" (PDF) .— da numerosos ejemplos
- ^ Ptolomeo, Claudio (1998) [100–170 d. C.]. "Libro VI". Almagesto de Ptolomeo . Traducido por Toomer, G. J. Princeton, NJ: Princeton University Press. pp. 306–307.
Enlaces externos
- El convertidor de números griegos


