Sexagésimo
| Parte de una serie sobre |
| Sistemas de numeración |
|---|
| Lista de sistemas de numeración |
Sexagesimal , también conocido como base 60 , [1] es un sistema de numeración que tiene como base sesenta . Se originó con los antiguos sumerios en el tercer milenio a. C., se transmitió a los antiguos babilonios y todavía se usa, en una forma modificada, para medir el tiempo , los ángulos y las coordenadas geográficas .
El número 60, un número compuesto superior , tiene doce divisores , a saber, 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60, de los cuales 2, 3 y 5 son números primos . Con tantos factores, muchas fracciones que involucran números sexagesimales se simplifican. Por ejemplo, una hora se puede dividir de manera uniforme en secciones de 30 minutos, 20 minutos, 15 minutos, 12 minutos, 10 minutos, 6 minutos, 5 minutos, 4 minutos, 3 minutos, 2 minutos y 1 minuto. 60 es el número más pequeño que es divisible por cada número del 1 al 6; es decir, es el mínimo común múltiplo de 1, 2, 3, 4, 5 y 6.
En este artículo, todos los dígitos sexagesimales se representan como números decimales, salvo que se indique lo contrario. Por ejemplo, el dígito sexagesimal más grande es "59".
Origen
Según Otto Neugebauer , los orígenes de la notación sexagesimal no son tan simples, consistentes o singulares en el tiempo como a menudo se los describe. A lo largo de sus muchos siglos de uso, que continúan hoy en día para temas especializados como el tiempo, los ángulos y los sistemas de coordenadas astronómicas, las notaciones sexagesimales siempre han contenido un fuerte trasfondo de notación decimal, como en la forma en que se escriben los dígitos sexagesimales. Su uso también siempre ha incluido (y continúa incluyendo) inconsistencias en dónde y cómo se representan los números en las distintas bases, incluso dentro de un mismo texto. [2]

El factor más poderoso para el uso riguroso y completamente autoconsistente del sexagesimal siempre ha sido sus ventajas matemáticas para escribir y calcular fracciones. En los textos antiguos esto se muestra en el hecho de que el sexagesimal se usa de manera más uniforme y consistente en las tablas matemáticas de datos. [2] Otro factor práctico que ayudó a expandir el uso del sexagesimal en el pasado, aunque de manera menos consistente que en las tablas matemáticas, fueron sus decididas ventajas para los comerciantes y compradores para facilitar las transacciones financieras cotidianas cuando implicaban negociar y dividir grandes cantidades de bienes. A fines del tercer milenio a. C., las unidades de peso sumerias/acadias incluían el kakkaru ( talento , aproximadamente 30 kg) dividido en 60 manû ( mina ), que a su vez se subdividía en 60 šiqlu ( shekel ); los descendientes de estas unidades persistieron durante milenios, aunque los griegos luego forzaron esta relación a la proporción más compatible con la base 10 de un shekel siendo una quincuagésima parte de una mina .
Aparte de las tablas matemáticas, las inconsistencias en la forma en que se representaban los números en la mayoría de los textos se extendían hasta los símbolos cuneiformes más básicos utilizados para representar cantidades numéricas. [2] Por ejemplo, el símbolo cuneiforme para el 1 era una elipse hecha aplicando el extremo redondeado del estilete en ángulo sobre la arcilla, mientras que el símbolo sexagesimal para el 60 era un óvalo más grande o un "1 grande". Pero dentro de los mismos textos en los que se usaban estos símbolos, el número 10 se representaba como un círculo hecho aplicando el extremo redondo del estilete perpendicular a la arcilla, y se usaba un círculo más grande o un "10 grande" para representar el 100. Estos símbolos numéricos de cantidades de múltiples bases podían mezclarse entre sí y con abreviaturas, incluso dentro de un mismo número. Los detalles e incluso las magnitudes implicadas (ya que el cero no se usaba de manera consistente ) eran idiomáticos para los períodos de tiempo, las culturas y las cantidades o conceptos particulares que se representaban. Si bien estas representaciones de cantidades numéricas dependientes del contexto son fáciles de criticar en retrospectiva, en los tiempos modernos aún tenemos docenas de ejemplos de uso regular de mezcla de bases dependientes del tema, incluida la reciente innovación de agregar fracciones decimales a coordenadas astronómicas sexagesimales. [2]
Uso
Matemáticas babilónicas
El sistema sexagesimal utilizado en la antigua Mesopotamia no era un sistema de base 60 puro, en el sentido de que no utilizaba 60 símbolos distintos para sus dígitos . En cambio, los dígitos cuneiformes utilizaban diez como subbase a la manera de una notación de valor de signo : un dígito sexagesimal estaba compuesto por un grupo de marcas estrechas en forma de cuña que representaban unidades de hasta nueve ( ,
, ,
,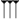 ,
,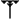 , ...,
, ..., ) y un grupo de marcas anchas en forma de cuña que representan hasta cinco decenas (
) y un grupo de marcas anchas en forma de cuña que representan hasta cinco decenas (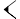 ,
, ,
, ,
, ,
, ). El valor del dígito era la suma de los valores de sus partes componentes:
). El valor del dígito era la suma de los valores de sus partes componentes:

Los números mayores de 59 se indicaban mediante bloques de símbolos múltiples de esta forma en la notación de valor posicional . Debido a que no había un símbolo para el cero, no siempre es inmediatamente obvio cómo debe interpretarse un número, y su valor verdadero a veces debe haber sido determinado por su contexto. Por ejemplo, los símbolos para 1 y 60 son idénticos. [3] [4] Los textos babilónicos posteriores utilizaron un marcador de posición (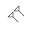 ) para representar el cero, pero sólo en las posiciones mediales, y no en el lado derecho del número, como en números como13 200 . [4]
) para representar el cero, pero sólo en las posiciones mediales, y no en el lado derecho del número, como en números como13 200 . [4]
Otros usos históricos

En el calendario chino se utiliza habitualmente un sistema en el que los días o años se nombran por posiciones en una secuencia de diez tallos y en otra secuencia de doce ramas. El mismo tallo y rama se repiten cada 60 pasos a lo largo de este ciclo.
El libro VIII de la República de Platón incluye una alegoría del matrimonio centrada en el número 60 4 =12 960 000 y sus divisores. Este número tiene la representación sexagesimal particularmente simple 1,0,0,0,0. Los estudiosos posteriores han invocado tanto las matemáticas babilónicas como la teoría musical en un intento de explicar este pasaje. [5]
El Almagesto de Ptolomeo , un tratado sobre astronomía matemática escrito en el siglo II d. C., utiliza la base 60 para expresar las partes fraccionarias de los números. En particular, su tabla de acordes , que fue esencialmente la única tabla trigonométrica extensa durante más de un milenio, tiene las partes fraccionarias de un grado en base 60, y era prácticamente equivalente a una tabla moderna de valores de la función seno .
Los astrónomos medievales también utilizaban números sexagesimales para medir el tiempo. Al-Biruni fue el primero en subdividir la hora sexagesimalmente en minutos , segundos , tercios y cuartos en 1000 mientras hablaba de los meses judíos. [6] Alrededor de 1235, Juan de Sacrobosco continuó esta tradición, aunque Nothaft pensó que Sacrobosco fue el primero en hacerlo. [7] La versión parisina de las tablas alfonsinas (ca. 1320) utilizaba el día como unidad básica de tiempo, registrando múltiplos y fracciones de un día en notación de base 60. [8]
El sistema de numeración sexagesimal siguió siendo utilizado frecuentemente por los astrónomos europeos para realizar cálculos hasta 1671. [9] Por ejemplo, Jost Bürgi en Fundamentum Astronomiae (presentado al emperador Rodolfo II en 1592), su colega Ursus en Fundamentum Astronomicum y posiblemente también Henry Briggs , utilizaron tablas de multiplicar basadas en el sistema sexagesimal a finales del siglo XVI para calcular senos. [10]
A finales del siglo XVIII y principios del XIX, se descubrió que los astrónomos tamiles realizaban cálculos astronómicos, utilizando conchas como base una mezcla de notaciones decimales y sexagesimales desarrolladas por astrónomos helenísticos . [11]
Los sistemas de numeración de base 60 también se han utilizado en algunas otras culturas que no están relacionadas con los sumerios, por ejemplo, por el pueblo Ekari de Nueva Guinea Occidental . [12] [13]
Uso moderno
Los usos modernos del sistema sexagesimal incluyen la medición de ángulos , coordenadas geográficas , navegación electrónica y tiempo . [14]
Una hora de tiempo se divide en 60 minutos y un minuto se divide en 60 segundos. Por lo tanto, una medida de tiempo como 3:23:17 (3 horas, 23 minutos y 17 segundos) se puede interpretar como un número sexagesimal entero (sin punto sexagesimal), es decir, 3 × 60 2 + 23 × 60 1 + 17 × 60 0 segundos . Sin embargo, cada uno de los tres dígitos sexagesimales de este número (3, 23 y 17) se escribe utilizando el sistema decimal .
De manera similar, la unidad práctica de medida angular es el grado , de los cuales hay 360 (seis sesenta) en un círculo. Hay 60 minutos de arco en un grado y 60 segundos de arco en un minuto.
YAML
En la versión 1.1 [15] del formato de almacenamiento de datos YAML , se admiten sexagesimales para escalares simples y se especifican formalmente tanto para números enteros [16] como para números de punto flotante. [17] Esto ha provocado confusión, ya que, por ejemplo, algunas direcciones MAC se reconocerían como sexagesimales y se cargarían como números enteros, mientras que otras no y se cargarían como cadenas. En YAML 1.2, se eliminó la compatibilidad con sexagesimales. [18]
Notaciones
En los textos astronómicos griegos helenísticos , como los escritos de Ptolomeo , los números sexagesimales se escribían utilizando numerales alfabéticos griegos , y cada dígito sexagesimal se trataba como un número distinto. Los astrónomos helenísticos adoptaron un nuevo símbolo para el cero,—°, que se transformó a lo largo de los siglos en otras formas, incluida la letra griega omicron, ο, que normalmente significa 70, pero es permisible en un sistema sexagesimal donde el valor máximo en cualquier posición es 59. [19] [20] Los griegos limitaron su uso de números sexagesimales a la parte fraccionaria de un número. [21]
En los textos latinos medievales, los números sexagesimales se escribían utilizando números arábigos ; los diferentes niveles de fracciones se denotaban minuta (es decir, fracción), minuta secunda , minuta tertia , etc. En el siglo XVII se volvió común denotar la parte entera de los números sexagesimales con un cero superíndice, y las diversas partes fraccionarias con uno o más acentos. John Wallis , en su Mathesis universalis , generalizó esta notación para incluir múltiplos superiores de 60; dando como ejemplo el número 49‵‵‵‵36‵‵‵25‵‵15‵1°15′2″36‴49⁗ ; donde los números a la izquierda se multiplican por potencias mayores de 60, los números a la derecha se dividen por potencias de 60 y el número marcado con el cero superíndice se multiplica por 1. [22] Esta notación conduce a los signos modernos para grados, minutos y segundos. La misma nomenclatura de minutos y segundos también se utiliza para unidades de tiempo, y la notación moderna para el tiempo con horas, minutos y segundos escritos en decimal y separados entre sí por dos puntos puede interpretarse como una forma de notación sexagesimal.
En algunos sistemas de uso, cada posición después del punto sexagesimal se numeraba, utilizando raíces latinas o francesas: prime o primus , seconde o secundus , tierce , quatre , quinte , etc. Hasta el día de hoy llamamos "segundo" a la parte de segundo orden de una hora o de un grado . Hasta al menos el siglo XVIII, 1/60 de un segundo se llamaba "terce" o "tercera". [23] [24]
En la década de 1930, Otto Neugebauer introdujo un sistema de notación moderno para los números babilónicos y helenísticos que sustituye la notación decimal moderna de 0 a 59 en cada posición, mientras que utiliza un punto y coma (;) para separar las partes enteras y fraccionarias del número y una coma (,) para separar las posiciones dentro de cada parte. [25] Por ejemplo, el mes sinódico medio utilizado tanto por los astrónomos babilónicos como por los helenísticos y que todavía se utiliza en el calendario hebreo es 29;31,50,8,20 días. Esta notación se utiliza en este artículo.
Fracciones y números irracionales
Fracciones
En el sistema sexagesimal, cualquier fracción en la que el denominador sea un número regular (que tenga sólo 2, 3 y 5 en su factorización prima ) puede expresarse de forma exacta. [26] Aquí se muestran todas las fracciones de este tipo en las que el denominador es menor o igual a 60:
- 1 ⁄ 2 = 0;30
- 1 ⁄ 3 = 0;20
- 1 ⁄ 4 = 0;15
- 1 ⁄ 5 = 0;12
- 1 ⁄ 6 = 0;10
- 1 ⁄ 8 = 0;7,30
- 1 ⁄ 9 = 0;6,40
- 1 ⁄ 10 = 0;6
- 1 ⁄ 12 = 0;5
- 1 ⁄ 15 = 0;4
- 1 ⁄ 16 = 0;3,45
- 1 ⁄ 18 = 0;3,20
- 1 ⁄ 20 = 0;3
- 1 ⁄ 24 = 0;2,30
- 1 ⁄ 25 = 0;2,24
- 1 ⁄ 27 = 0;2,13,20
- 1 ⁄ 30 = 0;2
- 1 ⁄ 32 = 0;1,52,30
- 1 ⁄ 36 = 0;1,40
- 1 ⁄ 40 = 0;1,30
- 1 ⁄ 45 = 0;1,20
- 1 ⁄ 48 = 0;1,15
- 1 ⁄ 50 = 0;1,12
- 1 ⁄ 54 = 0;1,6,40
- 1 ⁄ 60 = 0;1
Sin embargo, los números que no son regulares forman fracciones repetidas más complicadas . Por ejemplo:
- 1 ⁄ 7 = 0; 8,34,17 (la barra indica la secuencia de dígitos sexagesimales 8,34,17 se repite infinitas veces)
- 1 ⁄ 11 = 0; 5,27,16,21,49
- 1 ⁄ 13 = 0; 4,36,55,23
- 1 ⁄ 14 = 0;4, 17,8,34
- 1 ⁄ 17 = 0; 3,31,45,52,56,28,14,7
- 1 ⁄ 19 = 0; 3,9,28,25,15,47,22,6,18,56,50,31,34,44,12,37,53,41
- 1 ⁄ 59 = 0; 1
- 1 ⁄ 61 = 0; 0,59
El hecho de que los dos números adyacentes a sesenta, 59 y 61, sean ambos números primos implica que las fracciones que se repiten con un período de uno o dos dígitos sexagesimales solo pueden tener como denominadores números regulares múltiplos de 59 o 61, y que otros números no regulares tienen fracciones que se repiten con un período más largo.
Números irracionales

Las representaciones de números irracionales en cualquier sistema numérico posicional (incluidos el decimal y el sexagesimal) no terminan ni se repiten .
La raíz cuadrada de 2 , la longitud de la diagonal de un cuadrado unitario , fue aproximada por los babilonios del Período Babilónico Antiguo ( 1900 a. C. – 1650 a. C. ) como
- [27]
Porque √ 2 ≈ 1.414 213 56 ... es un número irracional , no se puede expresar exactamente en sexagesimal (o en cualquier sistema de base entera), pero su expansión sexagesimal comienza 1;24,51,10,7,46,6,4,44... ( OEIS : A070197 )
El valor de π utilizado por el matemático y científico griego Ptolomeo era 3;8,30 = 3 + 8/60 + 30/60 2 = 377/120 ≈3.141 666 .... [28] Jamshīd al-Kāshī , un matemático persa del siglo XV , calculó 2 π como una expresión sexagesimal a su valor correcto cuando se redondeó a nueve subdígitos (es decir, a 1/60 9 ); su valor para 2 π fue 6;16,59,28,1,34,51,46,14,50. [29] [30] Al igual que √ 2 arriba, 2 π es un número irracional y no se puede expresar exactamente en sexagesimal. Su expansión sexagesimal comienza 6;16,59,28,1,34,51,46,14,49,55,12,35... ( OEIS : A091649 )
Véase también
Referencias
- ^ Se pronuncia / s ɛ k s ə ˈ dʒ ɛ s ɪ m əl / y / s ɛ k ˈ s æ dʒ ɪ n ər i / ; ver "sexagesimal" , Oxford English Dictionary (edición en línea), Oxford University Press (se requiere suscripción o membresía de institución participante)
- ^ abcd Neugebauer, O. (1969), "Las ciencias exactas en la antigüedad", Acta Historica Scientiarum Naturalium et Medicinalium , 9 , Dover: 17-19, ISBN 0-486-22332-9, PMID14884919
- ^ Bello, Ignacio; Britton, Jack R.; Kaul, Anton (2009), Temas de matemáticas contemporáneas (9.ª ed.), Cengage Learning, pág. 182, ISBN 9780538737791.
- ^ ab Lamb, Evelyn (31 de agosto de 2014), "Mira, mamá, ¡no hay cero!", Scientific American , Roots of Unity
- ^ Barton, George A. (1908), "Sobre el origen babilónico del número nupcial de Platón", Journal of the American Oriental Society , 29 : 210–219, doi :10.2307/592627, JSTOR 592627McClain , Ernest G .; Platón (1974), "Matrimonios" musicales en la "República" de Platón", Revista de teoría musical , 18 (2): 242–272, doi :10.2307/843638, JSTOR 843638
- ↑ Al-Biruni (1879) [1000], La cronología de las naciones antiguas, traducido por Sachau, C. Edward, págs. 147-149
- ^ Nothaft, C. Philipp E. (2018), Error escandaloso: reforma del calendario y astronomía calendárica en la Europa medieval , Oxford: Oxford University Press, pág. 126, ISBN 9780198799559Sacrobosco
pasó a las fracciones sexagesimales, pero las hizo más apropiadas para el uso computacional al aplicarlas no al día sino a la hora, inaugurando así el uso de horas, minutos y segundos que todavía prevalece en el siglo XXI.
- ^ Nothaft, C. Philipp E. (2018), Error escandaloso: reforma del calendario y astronomía calendárica en la Europa medieval , Oxford: Oxford University Press, pág. 196, ISBN 9780198799559Una característica notable de las Tablas Alfonsinas en su encarnación latino-parisina es la estricta 'sexagesimalización' de todos los parámetros tabulados ,
ya que... los movimientos y los intervalos de tiempo se disolvieron consistentemente en múltiplos de base 60 y fracciones de días o grados.
- ^ Newton, Isaac (1671), El método de fluxiones y series infinitas: con su aplicación a la geometría de líneas curvas, Londres : Henry Woodfall (publicado en 1736), pág. 146,
La más notable de ellas es la escala sexagenaria o sexagesimal de aritmética, de uso frecuente entre los astrónomos, que expresa todos los números posibles, enteros o fracciones, racionales o singulares, mediante las potencias de
sesenta
y ciertos coeficientes numéricos que no exceden de cincuenta y nueve.
- ^ Folkerts, Menso; Launert, Dieter; Thom, Andreas (2016), "Método de Jost Bürgi para calcular los senos", Historia Mathematica , 43 (2): 133–147, arXiv : 1510.03180 , doi :10.1016/j.hm.2016.03.001, MR 3489006, S2CID 119326088
- ^ Neugebauer, Otto (1952), "Astronomía tamil: un estudio sobre la historia de la astronomía en la India", Osiris , 10 : 252–276, doi :10.1086/368555, S2CID 143591575; reimpreso en Neugebauer, Otto (1983), Astronomía e historia: ensayos seleccionados , Nueva York: Springer-Verlag , ISBN 0-387-90844-7
- ^ Bowers, Nancy (1977), "Numeración kapauku: cálculo, racismo, erudición y sistemas de conteo melanesios" (PDF) , Journal of the Polynesian Society , 86 (1): 105–116, archivado desde el original (PDF) el 2009-03-05
- ^ Lean, Glendon Angove (1992), Sistemas de conteo de Papua Nueva Guinea y Oceanía, tesis doctoral, Universidad Tecnológica de Papua Nueva Guinea , archivada desde el original el 5 de septiembre de 2007. Véase especialmente el capítulo 4. Archivado el 28 de septiembre de 2007 en Wayback Machine .
- ^ Powell, Marvin A. (2008). "Sistema sexagesimal". Enciclopedia de la historia de la ciencia, la tecnología y la medicina en culturas no occidentales . pp. 1998-1999. doi :10.1007/978-1-4020-4425-0_9055. ISBN . 978-1-4020-4559-2.
- ^ "YAML no es un lenguaje de marcado (YAML™) versión 1.1".
- ^ "Tipo entero independiente del lenguaje para YAML versión 1.1".
- ^ "Tipo de punto flotante independiente del lenguaje para YAML™ versión 1.1".
- ^ Oren Ben-Kiki; Clark Evans; Brian Ingerson (1 de octubre de 2009), "YAML Ain't Markup Language (YAML™) Version 1.2 (3rd Edition, Patched at 2009-10-01) §10.3.2 Tag Resolution", El sitio web oficial de YAML , consultado el 30 de enero de 2019
- ^ Neugebauer, Otto (1969) [1957], "Las ciencias exactas en la antigüedad", Acta Historica Scientiarum Naturalium et Medicinalium , 9 (2 ed.), Publicaciones de Dover : 13-14, lámina 2, ISBN 978-0-486-22332-2, PMID14884919
- ^ Mercier, Raymond, "Consideración del símbolo griego 'cero'" (PDF) , Página de inicio de Kairos
- ^ Aaboe, Asger (1964), Episodios de la historia temprana de las matemáticas , New Mathematical Library, vol. 13, Nueva York: Random House, págs. 103-104
- ^ Cajori, Florian (2007) [1928], Una historia de las notaciones matemáticas, vol. 1, Nueva York: Cosimo, Inc., pág. 216, ISBN 9781602066854
- ^ Wade, Nicholas (1998), Una historia natural de la visión , MIT Press, p. 193, ISBN 978-0-262-73129-4
- ^ Lewis, Robert E. (1952), Diccionario de inglés medio , University of Michigan Press, pág. 231, ISBN 978-0-472-01212-1
- ^ Neugebauer, Otto ; Sachs, Abraham Joseph ; Götze, Albrecht (1945), Textos cuneiformes matemáticos, American Oriental Series, vol. 29, New Haven: American Oriental Society y las escuelas americanas de investigación oriental, pág. 2
- ^ Neugebauer, Otto E. (1955), Textos cuneiformes astronómicos , Londres: Lund Humphries
- ^ Fowler, David ; Robson, Eleanor (1998), "Aproximaciones de raíz cuadrada en las matemáticas babilónicas antiguas: YBC 7289 en contexto", Historia Mathematica , 25 (4): 366–378, doi : 10.1006/hmat.1998.2209 , MR 1662496
- ^ Toomer, GJ , ed. (1984), Almagesto de Ptolomeo , Nueva York: Springer Verlag, p. 302, ISBN 0-387-91220-7
- ^ Youschkevitch, Adolf P., "Al-Kashi", en Rosenfeld, Boris A. (ed.), Diccionario de biografía científica , pág. 256.
- ^ Aaboe (1964), pág. 125
Lectura adicional
- Ifrah, Georges (1999), La historia universal de los números: desde la prehistoria hasta la invención de la computadora , Wiley, ISBN 0-471-37568-3.
- Nissen, Hans J.; Damerow, P.; Englund, R. (1993), Contabilidad arcaica , University of Chicago Press, ISBN 0-226-58659-6
Enlaces externos
- "Hechos sobre el cálculo de grados y minutos" es un libro en lengua árabe de Sibṭ al-Māridīnī, Badr al-Dīn Muḥammad ibn Muḥammad (nacido en 1423). Esta obra ofrece un tratamiento muy detallado de las matemáticas sexagesimales e incluye lo que parece ser la primera mención de la periodicidad de las fracciones sexagesimales.
