Sistema de numeración alfabético
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (August 2022) |
| Part of a series on |
| Numeral systems |
|---|
| List of numeral systems |
Un sistema de numeración alfabético es un tipo de sistema de numeración . Desarrollado en la antigüedad clásica , floreció durante la Alta Edad Media . [1] En los sistemas de numeración alfabética, los números se escriben utilizando los caracteres de un alfabeto , silabario u otro sistema de escritura . A diferencia de los sistemas de numeración acrofónicos , donde un numeral se representa por la primera letra del nombre léxico del numeral, los sistemas de numeración alfabética pueden asignar letras arbitrariamente a valores numéricos. Algunos sistemas, incluidos los sistemas árabe , georgiano y hebreo , utilizan un orden alfabético ya establecido . [1] Los sistemas de numeración alfabética se originaron con los numerales griegos alrededor del 600 a. C. y se extinguieron en gran medida en el siglo XVI. [1] Después del desarrollo de los sistemas de numeración posicional como los numerales hindúes y árabes , el uso de los sistemas de numeración alfabética disminuyó a listas predominantemente ordenadas, paginación , funciones religiosas y magia adivinatoria. [1]
Historia
El primer sistema de numeración alfabético del que se tiene constancia es el sistema alfabético griego (denominado sistema jónico o milesio debido a su origen en el oeste de Asia Menor ). La estructura del sistema sigue la estructura de los números demóticos egipcios ; las letras griegas reemplazaron a los signos egipcios. Los primeros ejemplos del sistema griego datan del siglo VI a. C., escritos con las letras de la escritura griega arcaica utilizada en Jonia . [2]
Otras culturas en contacto con Grecia adoptaron esta notación numérica, reemplazando las letras griegas con su propia escritura; entre ellas, los hebreos a fines del siglo II a. C. El alfabeto gótico adoptó sus propios numerales alfabéticos junto con la escritura de influencia griega. [3] En el norte de África , el sistema copto se desarrolló en el siglo IV d. C., [4] y el sistema ge'ez en Etiopía se desarrolló alrededor del 350 d. C. [5] Ambos se desarrollaron a partir del modelo griego.
Los árabes desarrollaron su propio sistema de numeración alfabética, los numerales abyad , en el siglo VII d. C., y lo utilizaron con fines matemáticos y astrológicos incluso en el siglo XIII, mucho después de la introducción del sistema de numeración hindú-arábigo . [6] Después de la adopción del cristianismo, los armenios y los georgianos desarrollaron su sistema de numeración alfabética en el siglo IV o principios del V, mientras que en el Imperio bizantino se introdujeron los numerales cirílicos y el glagolítico en el siglo IX. Los sistemas de numeración alfabética se conocían y utilizaban tan al norte como Inglaterra, Alemania y Rusia, tan al sur como Etiopía, tan al este como Persia y en el norte de África desde Marruecos hasta Asia Central. [ cita requerida ]
Hacia el siglo XVI d. C., la mayoría de los sistemas de numeración alfabéticos habían desaparecido o eran poco utilizados, reemplazados por los numerales posicionales árabes y occidentales como los numerales ordinarios del comercio y la administración en toda Europa y Oriente Medio. [1]
Los sistemas de numeración alfabética más nuevos en uso, todos ellos posicionales, forman parte de los sistemas de escritura táctil para personas con discapacidad visual . Aunque el braille de 1829 tenía un sistema posicional cifrado simple copiado de los numerales occidentales con un símbolo separado para cada dígito, la experiencia temprana con estudiantes obligó a su diseñador Louis Braille a simplificar el sistema, reduciendo el número de patrones (símbolos) disponibles de 125 a 63, por lo que tuvo que reutilizar un símbolo complementario para marcar las letras a–j como numerales. Además de este sistema tradicional, se desarrolló otro en Francia en el siglo XX, y otro más en los EE. UU.
Sistemas
Un sistema de numeración alfabético emplea las letras de una escritura en el orden específico del alfabeto para expresar números.
En griego, las letras se asignan a los números respectivos en los siguientes conjuntos: del 1 al 9, del 10 al 90, del 100 al 900, etc. Los decimales se representan con un solo símbolo. Al final del alfabeto, los números superiores se representan con varios métodos multiplicativos. Sin embargo, dado que los sistemas de escritura tienen un número diferente de letras, otros sistemas de escritura no necesariamente agrupan los números de esta manera. El alfabeto griego tiene 24 letras; se tuvieron que incorporar tres letras adicionales para llegar a 900. A diferencia del griego, las 22 letras del alfabeto hebreo permitían la expresión numérica hasta 400. Los 28 signos consonánticos del abjad árabe podían representar números hasta 1000. Los alfabetos arameos antiguos tenían suficientes letras para llegar hasta 9000. En los manuscritos matemáticos y astronómicos, se utilizaron otros métodos para representar números mayores. Los números romanos y los números áticos , que también eran sistemas de numeración alfabéticos, se volvieron más concisos con el tiempo, pero exigieron que sus usuarios estuvieran familiarizados con muchos más signos. Los números acrofónicos no pertenecen a este grupo de sistemas porque sus letras numerales no siguen el orden de un alfabeto.
Estos diversos sistemas no tienen un rasgo o característica unificadora única. La estructura más común es la aditiva cifrada con base decimal, con o sin el uso de la estructuración aditiva multiplicativa para los números superiores. Las excepciones incluyen la notación armenia de Shirakatsi , que es aditiva multiplicativa y a veces utiliza una base 1000, y los sistemas de notación astronómica griega y árabe.
Signos numericos
Las tablas siguientes muestran las configuraciones numéricas alfabéticas de varios sistemas de escritura.
Números alfabéticos griegos – "números jonios" o "números milesios" – (letras minúsculas)
unidades alfa β gamma del mi ϛ o η θ 1 2 3 4 5 6 7 8 9 decenas yo k la micras no o o π ϟ 10 20 30 40 50 60 70 80 90 cientos ρ σ τ yo φ χ ψ ω ϡ 100 200 300 400 500 600 700 800 900 miles ͵α ͵β ͵γ ͵δ ͵ε ͵ϛ ͵ζ ͵η ͵θ 1000 2000 3000 4000 5000 6000 7000 8000 9000
Algunos números representados con numerales alfabéticos griegos :
- ͵γϡμβ = (3000 + 900 + 40 + 2) = 3942
- χξζ = (600 + 60 + 7) = 667
unidades Yo Yo Yo Yo Yo Yo Yo Yo Yo 1 2 3 4 5 6 7 8 9 decenas Yo Yo Yo Yo Yo Yo Yo Yo Yo 10 20 30 40 50 60 70 80 90 cientos Yo Yo Yo Yo 100 200 300 400 miles ' א ' ב ' ג ' ד ' Y ' 'Yo ' 'Yo 1000 2000 3000 4000 5000 6000 7000 8000 9000
El sistema de escritura hebreo tiene sólo veintidós signos consonánticos, por lo que los números pueden expresarse con signos individuales sólo hasta 400. Las centenas superiores – 500, 600, 700, 800 y 900 – pueden escribirse sólo con varias combinaciones aditivas-acumulativas de las centenas inferiores (la dirección de escritura es de derecha a izquierda): [7]
- תק = ( 400 +100) 500
- רת = (400 + 200)600
- תש = (400+300) 700
- y = (400+400) 800
- ת ר ר ק = 400+200+200+100 = 900
Signos numerales armenios (letras minúsculas):
unidades ա բ գ դ ե զ է ը թ 1 2 3 4 5 6 7 8 9 decenas ժ ի լ խ ծ կ հ ձ ղ 10 20 30 40 50 60 70 80 90 cientos ճ մ յ ն շ ո չ պ ջ 100 200 300 400 500 600 700 800 900 miles ռ ս վ տ ր ց ւ փ ք 1000 2000 3000 4000 5000 6000 7000 8000 9000 diez mil Y ֆ 10000 20000 346 = յխզ
A diferencia de muchos sistemas de numeración alfabéticos, el sistema armenio no utiliza la multiplicación por 1000 o 10 000 para expresar valores superiores, sino que los valores superiores se escribían con todas sus letras mediante numerales léxicos. [8]
Números más altos
A medida que el alfabeto se fue terminando, se utilizaron diversos métodos multiplicativos para la expresión de números superiores en los diferentes sistemas. En el sistema alfabético griego, para los múltiplos de 1.000, el signo hasta se colocaba a la izquierda debajo de un signo numeral para indicar que debía multiplicarse por 1.000. [9]
- β = 2
- ͵β = 2.000
- ͵κ = 20.000
Con un segundo nivel de método multiplicativo –la multiplicación por 10.000– se podía ampliar el conjunto de números. El método más común, utilizado por Aristarco , implicaba colocar una frase numérica encima de un carácter M grande (M = miríadas = 10.000) para indicar la multiplicación por 10.000. [10] Este método podía expresar números hasta 100.000.000 (10 8 ).
20,704 − (2 ⋅ 10,000 + 700 + 4) podría representarse como:
ψδ = 20,704
Según el relato de Pappus de Alejandría , Apolonio de Perge utilizó otro método. En él, los números por encima de M = miríadas = 10.000 representaban el exponente de 10.000. El número que se debía multiplicar por M se escribía después del carácter M. [11] Este método podía expresar 5.462.360.064.000.000 como:
͵EYZB ͵ΓX Año fiscal 10000 3 × 5462 + 10000 2 × 3600 + 10000 1 × 6400
Distinguir frases numerales del texto
Los números alfabéticos se diferenciaban de las palabras mediante signos especiales, generalmente un trazo horizontal sobre la frase numérica, pero en ocasiones se colocaban puntos a ambos lados. Esto último se manifestaba en el alfabeto griego con el signo hasta .

= 285
En los números etíopes , conocidos como ge'ez , los signos tienen marcas tanto por encima como por debajo para indicar que su valor es numérico. Los números etíopes son la excepción, donde los signos numerales no son letras de su escritura. Esta práctica se volvió universal a partir del siglo XV. [12]
Signos numerales de números etíopes con marcas tanto encima como debajo de las letras:
1 2 3 4 5 6 7 8 9 × 1 ፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ × 10 ፲ ፳ ፴ ፵ ፶ ፷ ፸ ፹ ፺ × 100 ፻ × 10.000 ፼
La dirección de los números sigue la dirección del sistema de escritura. La escritura se hace de izquierda a derecha en los números alfabéticos griegos, coptos, etíopes, góticos, armenios, georgianos, glagolíticos y cirílicos, junto con la notación de Shirakatsi. La escritura de derecha a izquierda se encuentra en los números alfabéticos hebreos y siríacos, los números abjad árabes y los números de Fez. [ cita requerida ]
Fracciones
Fracciones unitarias
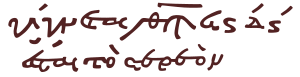
Las fracciones unitarias eran un método para expresar fracciones. En la notación alfabética griega, las fracciones unitarias se indicaban con el denominador –signo numérico alfabético– seguido de pequeños acentos o trazos colocados a la derecha de un numeral, conocidos como keraia (ʹ). Por lo tanto, γʹ indicaba un tercio, δʹ un cuarto, y así sucesivamente. Estas fracciones eran aditivas y también se conocían como fracciones egipcias .
Por ejemplo: δ´ ϛ´ = 1 ⁄ 4 + 1 ⁄ 6 = 5 ⁄ 12 .
Un número mixto podría escribirse así: ͵θϡϟϛ δ´ ϛ´ = 9996 + 1 ⁄ 4 + 1 ⁄ 6
Fracciones astronómicas

En muchos textos astronómicos, un conjunto distinto de sistemas de numeración alfabética combina sus numerales alfabéticos ordinarios con una base de 60, como los sistemas sexagesimales babilónicos . En el siglo II a. C., surgió un híbrido de notación babilónica y numerales alfabéticos griegos que se utilizó para expresar fracciones. [13] A diferencia del sistema babilónico, la base griega de 60 no se utilizó para expresar números enteros.
En este sistema posicional sexagesimal –con subbase 10– para expresar fracciones se utilizaban catorce de los numerales alfabéticos (las unidades del 1 al 9 y las décadas del 10 al 50) para escribir cualquier número del 1 al 59. Estos podían ser numerador de una fracción. El principio posicional se utilizaba para el denominador de una fracción, que se escribía con exponente 60 (60, 3.600, 216.000, etc.). Las fracciones sexagesimales podían utilizarse para expresar cualquier valor fraccionario, representando las posiciones sucesivas 1/60, 1/60 2 , 1/60 3 , etc. [14] El primer texto importante en el que apareció este sistema combinado fue el Almagesto de Ptolomeo , escrito en el siglo II d. C. [15]
Fracciones astronómicas (con signos alfabéticos griegos):
unidades alfa β gamma del mi ϛ o η θ 1 2 3 4 5 6 7 8 9 decenas yo k la micras no 10 20 30 40 50
͵αφιε κ ιε = 1515 + (20 x 1/60) + (15 x 1/3600) = 1515,3375
Este sistema combinado no utilizaba un punto de base , pero las fracciones astronómicas tenían un signo especial para indicar el cero como marcador de posición. Algunos textos babilónicos tardíos utilizaban un marcador de posición similar. Los griegos adoptaron esta técnica utilizando su propio signo, cuya forma y carácter cambiaron con el tiempo desde los manuscritos tempranos (siglo I d. C.) hasta una notación alfabética. [16]
Esta notación sexagesimal era especialmente útil en astronomía y matemáticas debido a la división del círculo en 360 grados (con subdivisiones de 60 minutos por grado y 60 segundos por minuto). En el comentario de Teón de Alejandría (siglo IV d. C.) sobre el Almagesto, la frase numeral ͵αφιε κ ιε expresa 1515 ( ͵αφιε ) grados, 20 ( κ ) minutos y 15 ( ιε ) segundos. [17] El valor del grado está en los números alfabéticos decimales ordinarios, incluido el uso del multiplicativo hasta para 1000, mientras que las dos últimas posiciones se escriben en fracciones sexagesimales.
Los árabes adoptaron fracciones astronómicas directamente de los griegos, y de manera similar los astrónomos hebreos utilizaron fracciones sexagesimales, pero los signos numerales griegos fueron reemplazados por sus propios signos numerales alfabéticos para expresar tanto números enteros como fracciones.
Sistemas de numeración alfabética
Véase también
Referencias
Citas
- ^ abcde Chrisomalis (2010), pág. 185.
- ^ Chrisomalis (2010), pág. 135–138.
- ^ Chrisomalis (2010), pág. 155.
- ^ Chrisomalis (2010), pág. 148.
- ^ Chrisomalis (2010), pág. 152.
- ^ Chrisomalis (2010), pág. 166.
- ^ Chrisomalis (2010), pág. 156.
- ^ Chrisomalis (2010), pág. 174.
- ^ Chrisomalis (2010), pág. 138.
- ^ Heath (1921), págs. 39–41.
- ^ Sistemas de numeración griegos – MacTutor
- ^ Ifrah (1998), págs. 246-247.
- ^ Ifrah (1998), pág. 156.
- ^ Chrisomalis (2010), pág. 169.
- ^ Heath (1921), págs. 44-45.
- ^ Iraní (1955).
- ^ Thomas (1962), págs. 50-51.
Bibliografía
- Chrisomalis, Stephen (2010). Notación numérica: una historia comparada. Cambridge University Press. pp. 133–187. ISBN 9780521878180.
- Heath, Thomas L. (1921). Una historia de las matemáticas griegas. 2 vols . Cambridge: Cambridge University Press.
- Ifrah, Georges (1998). La historia universal de los números: desde la prehistoria hasta la invención de la computadora . Traducido por Bellos, David. Londres: Harvill Press. ISBN. 9781860463242.
- Irani, Rida AK (1955). "Formas de numeración arábiga". Centaurus . 4 (1): 1–12. Código Bibliográfico :1955Cent....4....1I. doi :10.1111/j.1600-0498.1955.tb00464.x.
- Thomas, Ivor (1962). Selecciones que ilustran la historia de las matemáticas griegas . Vol. 1. Cambridge, MA: Harvard University Press.
Lectura adicional
- Bender, Marvin L., Sydney W. Head y Roger Cowley. 1976. El sistema de escritura etíope. En Language in Ethiopia , ML Bender, JD Bowen, RL Cooper y CA Ferguson, eds., págs. 120-129. Londres: Oxford University Press.
- Braune, Wilhelm y Ernst Ebbinghaus. 1966. Gótische Grammatik . Tubinga: Max Niemeyer Verlag.
- Colin, GS 1960. Abdjad. En Enciclopedia del Islam , vol. 1, págs. 97-98. Leiden: Brill.
- Colin, GS 1971. Hisab al-djummal. En Enciclopedia del Islam , vol. 3, pág. 468. Leiden: Brill.
- Cubberley, Paul. 1996. Los alfabetos eslavos. En The World's Writing Systems , Peter T. Daniels y William Bright, eds., págs. 346-355. Nueva York: Oxford University Press.
- Gandz, Solomon. 1933. Numerales hebreos. Actas de la Academia Estadounidense de Investigación Judía 4: págs. 53–112.
- Millard, A. 1995. Extranjeros de Egipto y Grecia: los signos de los números en el hebreo primitivo. En Inmigración y emigración en el antiguo Cercano Oriente , K. van Lerberghe y A. Schoors, eds., págs. 189-194. Lovaina: Peeters.
- Megally, Fuad (1991). "Sistema numérico copto". En Atiya, Azis S. (ed.). Coptic Encyclopedia . Nueva York: Macmillan. págs. 1820–1822.
- Messiha, Heshmat. 1994. Les chiffres coptes. Le Monde Copte 24: 25-28.
- Neugebauer, Otto (1979). Astronomía etíope y Computus . Viena: Verlag der Österreichischen Akademie der Wissenschaften.
- Pankhurst, Richard KP, ed. 1985. Cartas de gobernantes etíopes (principios y mediados del siglo XIX) , traducido por David L. Appleyard y AK Irvine. Oxford: Oxford University Press.
- Schanzlin, GL 1934. La notación abjad. El mundo musulmán 24: 257–261.
- Shaw, Allen A. 1938–9. Un sistema de numeración pasado por alto de la antigüedad. National Mathematics Magazine 13: 368–372.
- Smith, David E. y L. C Karpinski. 1911. Los números hindú-árabes. Boston: Ginn



