Números cuneiformes babilónicos

Los números cuneiformes babilónicos , también utilizados en Asiria y Caldea , se escribían en cuneiforme , utilizando un estilete de caña con punta de cuña para imprimir una marca en una tablilla de arcilla blanda que se exponía al sol para endurecerse y crear un registro permanente.
Los babilonios , que eran famosos por sus observaciones astronómicas, así como por sus cálculos (ayudados por su invención del ábaco ), utilizaban un sistema numérico posicional sexagesimal (base 60) heredado de las civilizaciones sumeria o acadia. [1] Ninguno de los predecesores era un sistema posicional (que tuviera una convención para la cual el "final" del numeral representaba las unidades).
Origen
Este sistema apareció por primera vez alrededor del año 2000 a. C.; [1] su estructura refleja los números léxicos decimales de las lenguas semíticas en lugar de los números léxicos sumerios. [2] Sin embargo, el uso de un signo sumerio especial para 60 (además de dos signos semíticos para el mismo número) [1] da fe de una relación con el sistema sumerio. [2]
| Parte de una serie sobre |
| Sistemas de numeración |
|---|
| Lista de sistemas de numeración |
Símbolos
Se considera que el sistema babilónico fue el primer sistema numérico posicional conocido , en el que el valor de un dígito en particular depende tanto del dígito en sí como de su posición dentro del número. Este fue un avance extremadamente importante porque los sistemas que no utilizan valores posicionales requieren símbolos únicos para representar cada potencia de una base (diez, cien, mil, etc.), lo que puede dificultar los cálculos.
Solo se utilizaron dos símbolos (𒁹 para contar unidades y 𒌋 para contar decenas) para indicar los 59 dígitos distintos de cero . Estos símbolos y sus valores se combinaron para formar un dígito en una notación de signo-valor bastante similar a la de los números romanos ; por ejemplo, la combinación 𒌋𒌋𒁹𒁹𒁹 representaba el dígito 23 (ver la tabla de dígitos anterior).
Estos dígitos se utilizaban para representar números mayores en el sistema posicional de base 60 (sexagesimal). Por ejemplo, 𒁹𒁹 𒌋𒌋𒁹𒁹𒁹 𒁹𒁹𒁹 representaría 2×60 2 +23×60+3 = 8583.
Se dejó un espacio para indicar un lugar sin valor, similar al cero moderno . Los babilonios idearon más tarde un signo para representar este lugar vacío. Carecían de un símbolo que cumpliera la función de punto de base , por lo que el lugar de las unidades debía inferirse del contexto: 𒌋𒌋𒁹𒁹𒁹 podría haber representado 23, 23×60 (𒌋𒌋𒁹𒁹𒁹␣), 23×60×60 (𒌋𒌋𒁹𒁹𒁹␣␣), o 23/60, etc.
Su sistema claramente usaba decimales internas para representar dígitos, pero no era realmente un sistema de base mixta 10 y 6, ya que la subbase diez se usaba simplemente para facilitar la representación del gran conjunto de dígitos necesarios, mientras que los valores de posición en una cadena de dígitos eran consistentemente de base 60 y la aritmética necesaria para trabajar con estas cadenas de dígitos era correspondientemente sexagesimal.
El legado del sexagesimal aún sobrevive hasta nuestros días, en forma de grados (360° en un círculo o 60° en un ángulo de un triángulo equilátero ), minutos de arco y segundos de arco en trigonometría y la medición del tiempo , aunque ambos sistemas son en realidad radix mixtos. [3]
Una teoría común es que 60 , un número compuesto superior (el anterior y el siguiente en la serie son 12 y 120 ), fue elegido debido a su factorización prima : 2×2×3×5, que lo hace divisible por 1 , 2 , 3 , 4 , 5 , 6 , 10 , 12 , 15 , 20 , 30 y 60. Los números enteros y las fracciones se representaban de forma idéntica: no se escribía un punto de base, sino que se aclaraba mediante el contexto.
Cero
Los babilonios no tenían técnicamente un dígito ni un concepto del número cero . Aunque entendían la idea de la nada , no lo consideraban un número, sino simplemente la falta de un número. Los textos babilónicos posteriores utilizaron un marcador de posición (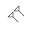 ) para representar el cero, pero sólo en las posiciones mediales, y no en el lado derecho del número, como lo hacemos en números como100 . [4]
) para representar el cero, pero sólo en las posiciones mediales, y no en el lado derecho del número, como lo hacemos en números como100 . [4]
Véase también
- Lengua acadia § Números
- Babilonia
- Babilonia
- Matemáticas babilónicas
- Historia de cero
- Sistema de numeración
- Lengua sumeria § Números
Referencias
- ^ abc Stephen Chrisomalis (2010). Notación numérica: una historia comparada . Cambridge University Press. pág. 247. ISBN 978-0-521-87818-0.
- ^ de Stephen Chrisomalis (2010). Notación numérica: una historia comparada . Cambridge University Press. pág. 248. ISBN 978-0-521-87818-0.
- ^ Scientific American – ¿Por qué un minuto se divide en 60 segundos, una hora en 60 minutos, pero un día sólo tiene 24 horas?
- ^ Lamb, Evelyn (31 de agosto de 2014), "Mira, mamá, ¡no hay cero!", Scientific American , Roots of Unity
Bibliografía
- Menninger, Karl W. (1969). Palabras y símbolos numéricos: una historia cultural de los números . MIT Press. ISBN 0-262-13040-8.
- McLeish, John (1991). Número: De las civilizaciones antiguas a la computadora . HarperCollins. ISBN 0-00-654484-3.
Enlaces externos
- Numerales babilónicos Archivado el 20 de mayo de 2017 en Wayback Machine.
- Números cuneiformes Archivado el 27 de junio de 2020 en Wayback Machine.
- Matemáticas babilónicas
- Fotografías de alta resolución, descripciones y análisis de la tablilla raíz(2) (YBC 7289) de la Colección Babilónica de Yale
- Fotografía, ilustración y descripción de la tablilla raíz(2) de la Colección Babilónica de Yale Archivado el 13 de agosto de 2012 en Wayback Machine.
- Numerales babilónicos por Michael Schreiber, Wolfram Demonstrations Project .
- Weisstein, Eric W. "Sexagesimal". MathWorld .
- CESCNC: un conversor de números práctico y fácil de usar

