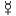3
Este artículo incluye una lista de referencias generales , pero carece de suficientes citas en línea correspondientes . ( febrero de 2024 ) |
| ||||
|---|---|---|---|---|
| Cardenal | tres | |||
| Ordinal | 3º (tercero) | |||
| Sistema de numeración | ternario | |||
| Factorización | principal | |||
| Principal | 2do | |||
| Divisores | 1, 3 | |||
| Número griego | Γ´ | |||
| Número romano | III, iii | |||
| Prefijo griego | tri- | |||
| Prefijo latino | tre-/ter- | |||
| Binario | 11 2 | |||
| Ternario | 10 3 | |||
| Senador | 3 6 | |||
| Octal | 3 8 | |||
| Duodecimal | 3 12 | |||
| Hexadecimal | 3 16 | |||
| Árabe , kurdo , persa , sindhi , urdu | 10 | |||
| Bengalí , asamés | ৩ | |||
| Chino | 三, 弎, 叄 | |||
| Devanagari | A | |||
| Dios mio | ፫ | |||
| Griego | γ (o Γ) | |||
| hebreo | Yo | |||
| japonés | 三/参 | |||
| Jemer | ៣ | |||
| armenio | ɳ | |||
| Malabar | Yo | |||
| Tamil | ௩ | |||
| Télugu | ౩ | |||
| Canarés | ೩ | |||
| tailandés | ๓ | |||
| N'Ko | ԃ | |||
| Laosiano | ໓ | |||
| georgiano | Ⴂ/ⴂ/გ ( Gani ) | |||
| Número babilónico | 𒐗 | |||
| Numerales mayas | ••• | |||
| Código morse | ... _ _ | |||
3 ( tres ) es un número , numeral y dígito . Es el número natural que sigue al 2 y precede al 4 , y es el número primo impar más pequeño y el único primo que precede a un número cuadrado. Tiene importancia religiosa y cultural en muchas sociedades.
Evolución del dígito árabe
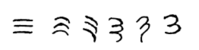
El uso de tres líneas para denotar el número 3 se produjo en muchos sistemas de escritura, incluidos algunos (como los numerales romanos y chinos ) que todavía se utilizan. Esa fue también la representación original del 3 en la notación numérica brahmica (india), sus primeras formas alineadas verticalmente. [1] Sin embargo, durante el Imperio Gupta , el signo se modificó mediante la adición de una curva en cada línea. La escritura Nāgarī rotó las líneas en el sentido de las agujas del reloj, por lo que aparecían horizontales, y finalizó cada línea con un trazo corto hacia abajo a la derecha. En la escritura cursiva, los tres trazos finalmente se conectaron para formar un glifo parecido a un ⟨3⟩ con un trazo adicional en la parte inferior: ३ .
Los dígitos indios se extendieron al Califato en el siglo IX. El trazo inferior se eliminó alrededor del siglo X en las partes occidentales del Califato, como el Magreb y Al-Ándalus , cuando se desarrolló una variante distinta ("árabe occidental") de los símbolos numéricos, incluido el moderno 3 occidental. En contraste, los árabes orientales conservaron y agrandaron ese trazo, rotando el dígito una vez más para obtener el dígito árabe moderno ("oriental") " ٣ ". [2]
En la mayoría de las tipografías occidentales modernas , el dígito 3, al igual que los demás dígitos decimales , tiene la altura de una letra mayúscula y se ubica sobre la línea base . En las tipografías con figuras de texto , por otro lado, el glifo suele tener la altura de una letra minúscula "x" y un descendente : " " Sin embargo, en algunos tipos de letra de texto en francés , tiene un ascendente en lugar de un descendente.
" Sin embargo, en algunos tipos de letra de texto en francés , tiene un ascendente en lugar de un descendente.
Una variante gráfica común del dígito tres tiene la parte superior plana, similar a la letra Ʒ (ezh). Esta forma se utiliza a veces para evitar que un 3 se falsifique como un 8. Se encuentra en los códigos de barras UPC-A y en las barajas estándar de 52 cartas .
Matemáticas
Según Pitágoras y la escuela pitagórica , el número 3, al que llamaban tríada , es el único número que es igual a la suma de todos los términos inferiores a él, y el único número cuya suma con los inferiores es igual al producto de ellos por sí mismo. [3]
Regla de divisibilidad
Un número natural es divisible por tres si la suma de sus dígitos en base 10 es divisible por 3. Por ejemplo, el número 21 es divisible por tres (3 por 7) y la suma de sus dígitos es 2 + 1 = 3. Debido a esto, el reverso de cualquier número que sea divisible por tres (o, de hecho, cualquier permutación de sus dígitos) también es divisible por tres. Por ejemplo, 1368 y su reverso 8631 son ambos divisibles por tres (y también lo son 1386, 3168, 3186, 3618, etc.). Véase también Regla de divisibilidad . Esto funciona en base 10 y en cualquier sistema de numeración posicional cuya base dividida por tres deje un resto de uno (bases 4, 7, 10, etc.).
Propiedades del numero
3 es el segundo número primo más pequeño y el primer número primo impar . Es el primer primo único , tal que el valor de la longitud del período de 1 de la expansión decimal de su recíproco , 0,333..., es único. 3 es un primo gemelo de 5 y primo primo de 7 , y el único número conocido tal que ! − 1 y ! + 1 son primos, así como el único número primo tal que − 1 produce otro número primo, 2. Un triángulo está formado por tres lados . Es el polígono más pequeño que no se autointersecta y el único polígono que no tiene diagonales propias . Al hacer estimaciones rápidas, 3 es una aproximación aproximada de π , 3,1415..., y una aproximación muy aproximada de e , 2,71828...
3 es el primer primo de Mersenne , así como el segundo exponente primo de Mersenne y el segundo doble exponente primo de Mersenne , para 7 y 127 , respectivamente. 3 es también el primero de los cinco primos de Fermat conocidos , que incluyen 5, 17 , 257 y 65537. Es el segundo primo de Fibonacci (y el segundo primo de Lucas ), el segundo primo de Sophie Germain , el tercer número de Harshad en base 10 y el segundo primo factorial , ya que es igual a 2! + 1.
3 es el segundo y único número triangular primo , y Gauss demostró que todo entero es la suma de como máximo 3 números triangulares .
Tres es el único número primo que es uno menos que un cuadrado perfecto . Cualquier otro número que sea − 1 para algún entero no es primo, ya que es ( − 1)( + 1). Esto también es cierto para 3 (con = 2), pero en este caso el factor más pequeño es 1. Si es mayor que 2, tanto − 1 como + 1 son mayores que 1, por lo que su producto no es primo.
Propiedades relacionadas
La trisección del ángulo fue uno de los tres famosos problemas de la antigüedad.
3 es el número de puntos no colineales necesarios para determinar un plano , un círculo y una parábola .
Sólo hay tres cuadrados panmágicos 4×4 distintos .
Tres de los cinco sólidos platónicos tienen caras triangulares: el tetraedro , el octaedro y el icosaedro . Además, tres de los cinco sólidos platónicos tienen vértices donde se encuentran tres caras: el tetraedro , el hexaedro ( cubo ) y el dodecaedro . Además, solo tres tipos diferentes de polígonos comprenden las caras de los cinco sólidos platónicos: el triángulo , el cuadrado y el pentágono .
Hay tres grupos finitos de politopos convexos uniformes en tres dimensiones, aparte de las infinitas familias de prismas y antiprismas : el grupo tetraédrico , el grupo octaédrico y el grupo icosaédrico . En dimensiones ⩾ 5, solo hay tres politopos regulares: los - símplex , los - cubos y los - ortoplex . En dimensiones ⩾ 9 , las únicas tres familias de politopos uniformes, aparte de las numerosas familias proprismáticas infinitas , son las familias símplex, cúbica y demihipercúbica . Para los panales hiperbólicos paracompactos , hay tres grupos en las dimensiones 6 y 9 , o equivalentemente de rangos 7 y 10, sin otras formas en dimensiones superiores. De los tres grupos finales, el más grande e importante es , que está asociado con un importante álgebra de Lie de Kac–Moody . [4]
Sistemas de numeración
Hay algunas evidencias que sugieren que el hombre primitivo pudo haber usado sistemas de conteo que consistían en "Uno, Dos, Tres" y luego "Muchos" para describir los límites de conteo. Los pueblos primitivos tenían una palabra para describir las cantidades de uno, dos y tres, pero cualquier cantidad más allá de esa cantidad se denotaba simplemente como "Muchos". Esto probablemente se basa en la prevalencia de este fenómeno entre personas de regiones tan dispares como las selvas profundas del Amazonas y Borneo, donde los exploradores de la civilización occidental tienen registros históricos de sus primeros encuentros con estos pueblos indígenas. [5]
Lista de cálculos básicos
| Multiplicación | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 50 | 100 | 1000 | 10000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 × x | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 | 63 | 66 | 69 | 72 | 75 | 150 | 300 | 3000 | 30000 |
| División | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 ÷ x | 3 | 1.5 | 1 | 0,75 | 0.6 | 0,5 | 0.428571 | 0,375 | 0.3 | 0.3 | 0.27 | 0,25 | 0.230769 | 0,2 142857 | 0,2 | 0,1875 | 0,1 7647058823529411 | 0,1 6 | 0,1 57894736842105263 | 0,15 | |
| x ÷3 | 0.3 | 0.6 | 1 | 1.3 | 1.6 | 2 | 2.3 | 2.6 | 3 | 3.3 | 3.6 | 4 | 4.3 | 4.6 | 5 | 5.3 | 5.6 | 6 | 6.3 | 6. 6 |
| Exponenciación | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 veces | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 | 177147 | 531441 | 1594323 | 4782969 | 14348907 | 43046721 | 129140163 | 387420489 | 1162261467 | 3486784401 | |
| x3 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 | 8000 |
Ciencia
- Tres es el número atómico del litio .
- Tres es el número de dimensiones que los humanos pueden percibir. Los humanos perciben el universo como si tuviera tres dimensiones espaciales , pero algunas teorías, como la teoría de cuerdas , sugieren que hay más. [6]
- Tres es el número de generaciones de fermiones elementales según el Modelo Estándar de física de partículas. [7]
- En física de partículas , cada protón o neutrón está compuesto de tres quarks . [8]
- Hay tres colores primarios en los modelos aditivo y sustractivo .
- La capacidad del ojo humano para distinguir colores se basa en la sensibilidad variable de las distintas células de la retina a la luz de distintas longitudes de onda . Como los humanos somos tricromáticos , la retina contiene tres tipos de células receptoras del color, o conos . [9]
- En física , los problemas de tres cuerpos no tienen una solución general en forma cerrada , a diferencia de los problemas de dos cuerpos . [10]
Ingeniería
- El triángulo , un polígono con tres aristas y tres vértices , es la forma física más estable. Por este motivo, se utiliza ampliamente en la construcción, la ingeniería y el diseño. [11]
Protociencia
- En la alquimia europea , los tres primos ( en latín : tria prima ) eran la sal (
 ), azufre (
), azufre ( ) y mercurio (
) y mercurio ( ). [12] [13]
). [12] [13] - Los tres doshas (debilidades) y sus antídotos son la base de la medicina ayurvédica en la India. [14]
Pseudociencia
- Tres es la representación simbólica del continente perdido de Mu , Augustus Le Plongeon y James Churchward . [15]
Filosofía
- Filósofos como Tomás de Aquino , Kant , Hegel , C. S. Peirce y Karl Popper han hecho divisiones triples, o tricotomías , que han sido importantes en su trabajo. [ cita requerida ]
- La dialéctica hegeliana de Tesis + Antítesis = Síntesis crea trinidad a partir de bianualidad. [ cita requerida ]
- En una entrevista de 1931, Nikola Tesla supuestamente dijo: "Si conocieras la magnificencia del 3, el 6 y el 9, entonces tendrías una clave para el universo". [ cita requerida ]
Religión
This section needs additional citations for verification. (October 2023) |

Muchas religiones del mundo contienen deidades triples o conceptos de trinidad, incluyendo la Trimurti y Tridevi hindúes , el Triglav (lit. "el de tres cabezas"), el dios principal de los eslavos , las tres Joyas del budismo , los tres Puros del taoísmo , la Santísima Trinidad cristiana y la Triple Diosa de la Wicca .

cristianismo
- El triple oficio de Cristo es una doctrina cristiana que establece que Cristo desempeña las funciones de profeta , sacerdote y rey .
- Durante la Agonía en el Huerto , Cristo pidió tres veces que le quitaran el cáliz.
- Jesús resucitó de entre los muertos al tercer día después de su muerte.
- El diablo tentó a Jesús tres veces.
- San Pedro negó tres veces a Jesús y tres veces afirmó su fe en Jesús .
- Los Magos – hombres sabios que eran astrónomos/astrólogos de Persia [16] – le dieron a Jesús tres regalos. [17] [18]
- Hay tres evangelios sinópticos y tres epístolas de Juan .
- El apóstol Pablo quedó ciego durante tres días después de su conversión al cristianismo .
judaísmo
- Noé tuvo tres hijos: Cam , Sem y Jafet.
- Los tres patriarcas : Abraham , Isaac y Jacob
- El profeta Balaam golpeó a su burro tres veces.
- El profeta Jonás pasó tres días y tres noches en el vientre de un gran pez.
- Tres divisiones de la Torá Escrita : Torá (Cinco Libros de Moisés), Nevi'im (Profetas), Ketuvim (Escritos) [19]
- Tres divisiones del pueblo judío: Kohen , Levita , Yisrael
- Tres oraciones diarias : Shacharit , Mincha , Maariv
- Tres comidas de Shabat
- Shabat termina cuando tres estrellas son visibles en el cielo nocturno [20]
- Tres fiestas de peregrinación : Pésaj , Shavuot y Sucot
- Tres matzos en la mesa del Séder de Pésaj [21]
- Las Tres Semanas , un período de duelo que une los días de ayuno del 17 de Tamuz y Tisha B'Av
- Tres pecados capitales por los cuales un judío debe morir antes que transgredirlos: idolatría , asesinato , inmoralidad sexual [22]
- Upsherin , el primer corte de pelo de un niño judío a los 3 años [23]
- Un Beth din está compuesto por tres miembros
- Tradicionalmente, a los potenciales conversos se les rechaza tres veces para poner a prueba su sinceridad [24].
- En la tradición mística judía de la Cábala , se cree que el alma consta de tres partes, siendo la más alta neshamah ("aliento"), la media ruach ("viento" o "espíritu") y la más baja nefesh ("reposo"). [25] A veces se mencionan adicionalmente los dos elementos Chayah ("vida" o "animal") y Yechidah ("unidad").
- En la Cabalá, el Árbol de la Vida (hebreo: Etz ha-Chayim , עץ החיים) se refiere a una última representación esquemática de tres pilares de su símbolo místico central, conocido como las 10 Sefirot .
islam
- Los tres principios fundamentales de la tradición chiíta: Tawhid (Unidad de Dios), Nabuwwa (Concepto de Profecía), Imama (Concepto de Imam)
Budismo
- Los Triple Bodhi (formas de entender el final del nacimiento) son Budhu, Pasebudhu y Mahaarahath.
- Las Tres Joyas , las tres cosas en las que los budistas se refugian.
sintoísmo
- La vestimenta imperial de Japón : la espada, el espejo y la joya.
Taoísmo
- Los Tres Tesoros ( chino :三寶; pinyin : sānbǎo ; Wade–Giles : san-pao ), las virtudes básicas del taoísmo .
- Los tres dantianos
- Tres líneas de un trigrama
- Tres Soberanos : Cielo Fu Xi (Mano – Cabeza – 3º Ojo), Humanidad Shen Nong ( Unidad 69 ), Infierno Nüwa (Pie – Abdomen – Ombligo).
hinduismo
- La Trimurti : Brahma el Creador, Vishnu el Preservador y Shiva el Destructor.
- Las tres guṇas ( triguna ) que se encuentran en la escuela Samkhya de la filosofía hindú. [26]
- Los tres caminos hacia la salvación en el Bhagavad Gita se llaman Karma Yoga , Bhakti Yoga y Jnana Yoga .
Zoroastrismo
- Las tres virtudes de Humata , Hukhta y Huvarshta (buenos pensamientos, buenas palabras y buenas acciones) son un principio básico del zoroastrismo .
Mitología nórdica
Tres es un número muy significativo en la mitología nórdica , junto con sus potencias 9 y 27.
- Antes del Ragnarök , habrá tres inviernos duros sin un verano intermedio, el Fimbulwinter .
- Odín soportó tres penurias en el Árbol del Mundo en su búsqueda de las runas : se ahorcó, se hirió con una lanza y sufrió hambre y sed.
- Bor tuvo tres hijos: Odín , Vili y Vé .
Otras religiones
- La regla de tres wiccana .
- La Triple Diosa : Doncella, Madre, Anciana; las tres parcas.
- Los hijos de Cronos : Zeus , Poseidón y Hades .
- El dios eslavo Triglav tiene tres cabezas.
Tradición esotérica
- La Sociedad Teosófica tiene tres condiciones de membresía :
- Los Tres Centros de Gurdjieff y la Ley de Tres .
- El Liber AL vel Legis , la escritura central de la religión de Thelema , consta de tres capítulos, correspondientes a tres narradores divinos respectivamente: Nuit , Hadit y Ra-Hoor-Khuit .
- La Triple Grandeza de Hermes Trimegisto es un tema importante en el hermetismo .
Como número de suerte o de mala suerte
This section needs additional citations for verification. (April 2009) |
Tres (三, escritura formal:叁, pinyin sān , cantonés : saam 1 ) se considera un buen número en la cultura china porque suena como la palabra "vivo" (生pinyin shēng , cantonés: saang 1 ), en comparación con cuatro (四, pinyin: sì , cantonés: sei 1 ), que suena como la palabra "muerte" (死pinyin sǐ , cantonés: sei 2 ).
Contar hasta tres es común en situaciones en las que un grupo de personas desea realizar una acción en sincronía : ahora, a la cuenta de tres, ¡todos tiran! Suponiendo que el contador avanza a un ritmo uniforme, los primeros dos conteos son necesarios para establecer el ritmo, y el conteo de "tres" se predice en función del tiempo del "uno" y el "dos" anteriores. Es probable que se use tres en lugar de algún otro número porque requiere la cantidad mínima de conteos al establecer un ritmo.
Existe otra superstición que dice que trae mala suerte encender un tercer fósforo o mechero , es decir, ser la tercera persona que enciende un cigarrillo con el mismo fósforo o mechero. Se afirma a veces que esta superstición se originó entre los soldados en las trincheras de la Primera Guerra Mundial, cuando un francotirador podía ver el primer fósforo, apuntar al segundo y disparar al tercero. [ cita requerida ]
La frase "la tercera es la vencida" se refiere a la superstición de que después de dos fracasos en cualquier empresa, es más probable que un tercer intento tenga éxito. Esto también se ve a veces al revés, como en "el tercer hombre [que hace algo, presumiblemente prohibido] es atrapado". [ cita requerida ]
A menudo se dice que la suerte , especialmente la mala suerte, "viene de tres en tres". [27]
Véase también
- Cubo (álgebra) – (3 superíndice )
- Tres veces
- Tercero
- Tríada
- Trío
- Regla de tres
- ɜ , U+025C ɜ LETRA MINÚSCULA LATINA E ABIERTA INVERTIDA también conocida como épsilon invertida
- Lista de carreteras numeradas 3
Referencias
- ^ Smith, David Eugene ; Karpinski, Louis Charles (1911). Los numerales indoarábigos. Boston; Londres: Ginn and Company. págs. 27–29, 40–41.
- ^ Georges Ifrah, La historia universal de los números: desde la prehistoria hasta la invención de la computadora , trad. David Bellos et al. Londres: The Harvill Press (1998): 393, fig. 24.63
- ^ Priya Hemenway (2005), Proporción divina: Phi en el arte, la naturaleza y la ciencia , Sterling Publishing Company Inc., págs. 53-54, ISBN 1-4027-3522-7
- ^ Allcock, Daniel (mayo de 2018). "Pares prenilpotentes en la red de raíces E10" (PDF) . Actas matemáticas de la Sociedad filosófica de Cambridge . 164 (3): 473–483. Código bibliográfico :2018MPCPS.164..473A. doi :10.1017/S0305004117000287. S2CID 8547735. Archivado (PDF) desde el original el 2022-11-03 . Consultado el 2022-11-03 .
- "Los detalles de la sección anterior eran específicos de E10, pero parece probable que la misma filosofía se aplique a los otros sistemas de raíces hiperbólicas simetrizables... parece valioso dar un esquema de cómo se realizarían los cálculos", considerando a E10 como un ejemplo modelo de simetrización de otros sistemas de raíces hiperbólicas E n .
- ^ Gribbin, Mary; Gribbin, John R.; Edney, Ralph; Halliday, Nicholas (2003). Grandes números . Cambridge: Wizard. ISBN 1840464313.
- ^ Zwiebach, Barton (2009). Un primer curso de teoría de cuerdas (2.ª ed.). Cambridge ; Nueva York: Cambridge University Press. ISBN 978-0-521-88032-9.
- ^ Harari, H. (1977). "Tres generaciones de quarks y leptones" (PDF) . En van Goeler, E.; Weinstein, R. (eds.). Actas del XII Rencontre de Moriond . pág. 170. SLAC-PUB-1974.
- ^ Adair, RK (1989). El gran diseño: partículas, campos y creación . Oxford University Press . pág. 214. Bibcode :1988gdpf.book.....A.
- ^ "Los bastones y conos del ojo humano". hyperphysics.phy-astr.gsu.edu . Consultado el 4 de junio de 2024 .
- ^ Barrow-Green, junio (2008). "El problema de los tres cuerpos". En Gowers, Timothy; Barrow-Green, junio; Leader, Imre (eds.). The Princeton Companion to Mathematics . Princeton University Press. págs. 726–728.
- ^ "La forma más estable: el triángulo". Matemáticas en la ciudad . Consultado el 23 de febrero de 2015.
- ^ Eric John Holmyard. Alquimia. 1995. pág. 153.
- ^ Walter J. Friedlander. La varita de oro de la medicina: una historia del símbolo del caduceo en la medicina. 1992. p.76-77
- ^ Kreidler, Marc (14 de diciembre de 2017). "Ayurveda: superstición antigua, no sabiduría antigua". Skeptical Inquirer . Consultado el 4 de junio de 2024 .
- ^ Churchward, James (1931). «El continente perdido de Mu: símbolos, viñetas, cuadros y diagramas». Biblioteca Pleyades . Archivado desde el original el 18 de julio de 2015. Consultado el 15 de marzo de 2016 .
- ^ Windle, Bryan (22 de diciembre de 2022). "¿Quiénes eran los magos?". Informe de arqueología bíblica . Consultado el 5 de julio de 2024 .
- ^ "Enciclopedia Británica". Lexikon des Gesamten Buchwesens Online (en alemán). doi : 10.1163/9789004337862_lgbo_com_050367.
- ^ "The Encyclopaedia Britannica". Nature . XV (378): 269–271. 25 de enero de 1877. Archivado desde el original el 24 de julio de 2020 . Consultado el 12 de julio de 2019 .
- ^ Marcus, Rabino Yossi (2015). "¿Por qué muchas cosas en el judaísmo se hacen tres veces?". Pregúntale a Moisés . Archivado desde el original el 2 de abril de 2015. Consultado el 16 de marzo de 2015 .
- ^ "Shabat". Judaísmo 101. 2011. Archivado desde el original el 29 de junio de 2009. Consultado el 16 de marzo de 2015 .
- ^ Kitov, Eliyahu (2015). "Las tres matzot". Chabad.org . Archivado desde el original el 24 de marzo de 2015. Consultado el 16 de marzo de 2015 .
- ^ Kaplan, Rabino Aryeh (28 de agosto de 2004). "Judaísmo y martirio". Aish.com. Archivado desde el original el 20 de marzo de 2015. Consultado el 16 de marzo de 2015 .
- ^ "Los conceptos básicos del Upsherin: el primer corte de pelo de un niño". Chabad.org . 2015. Archivado desde el original el 22 de marzo de 2015. Consultado el 16 de marzo de 2015 .
- ^ "El proceso de conversión". Centro de Conversión al Judaísmo. Archivado desde el original el 23 de febrero de 2021. Consultado el 16 de marzo de 2015 .
- ^ Kaplan, Aryeh. "El alma". Archivado el 24 de febrero de 2015 en Wayback Machine . Aish . De The Handbook of Jewish Thought (Vol. 2, Maznaim Publishing . Reimpreso con autorización). 4 de septiembre de 2004. Consultado el 24 de febrero de 2015.
- ^ James G. Lochtefeld, Guna, en La enciclopedia ilustrada del hinduismo: AM, vol. 1, Rosen Publishing, ISBN 978-0-8239-3179-8 , página 265
- ^ Véase "malo Archivado el 2 de marzo de 2009 en Wayback Machine " en el Oxford Dictionary of Phrase and Fable , 2006, a través de Encyclopedia.com.
- Wells, D. Diccionario Penguin de números curiosos e interesantes . Londres: Penguin Group. (1987): 46–48
Enlaces externos
- Libro triciclopédico de los tres de Michael Eck
- Los tres en la anatomía humana, por John A. McNulty
- Grime, James. "El 3 está en todas partes". Numberphile . Brady Haran . Archivado desde el original el 2013-05-14 . Consultado el 2013-04-13 .
- El número 3
- El entero positivo 3
- Curiosidades principales: 3