Distribución normal

Distribución normal
	Función de densidad de probabilidad 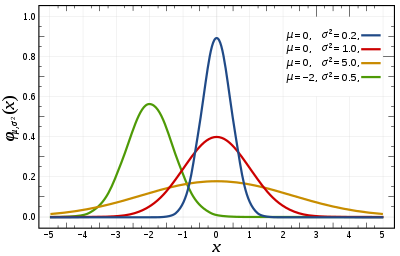La curva roja es la distribución normal estándar .
	Función de distribución acumulativa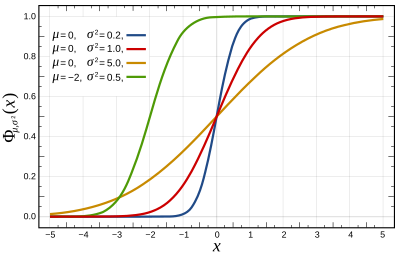
Notación	norte ( micras , σ 2 ) {\displaystyle {\mathcal {N}}(\mu,\sigma ^{2})}
Parámetros	micras ∈ R {\displaystyle \mu \in \mathbb {R}} = media ( ubicación ) = varianza ( escala al cuadrado ); σ 2 ∈ R > 0 {\displaystyle \sigma ^{2}\in \mathbb {R} _{>0}}
Apoyo	incógnita ∈ R {\displaystyle x\in \mathbb {R}}
PDF	1 2 π σ 2 mi − ( incógnita − micras ) 2 2 σ 2 {\displaystyle {\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}
CDF	Φ ( incógnita − micras σ ) = 1 2 [ 1 + campo ⁡ ( incógnita − micras σ 2 ) ] {\displaystyle \Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]}
Cuantil	micras + σ 2 campo − 1 ⁡ ( 2 pag − 1 ) {\displaystyle \mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2p-1)}
Significar	micras {\estilo de visualización \mu}
Mediana	micras {\estilo de visualización \mu}
Modo	micras {\estilo de visualización \mu}
Diferencia	σ 2 {\displaystyle \sigma ^{2}}
ENOJADO	σ 2 / π {\displaystyle \sigma {\sqrt {2/\pi }}}
Oblicuidad	0 {\estilo de visualización 0}
Exceso de curtosis	0 {\estilo de visualización 0}
Entropía	1 2 registro ⁡ ( 2 π mi σ 2 ) {\displaystyle {\frac {1}{2}}\log(2\pi e\sigma ^{2})}
MGF	exp ⁡ ( micras a + σ 2 a 2 / 2 ) {\displaystyle \exp(\mu t+\sigma ^{2}t^{2}/2)}
CF	exp ⁡ ( i micras a − σ 2 a 2 / 2 ) {\displaystyle \exp(i\mu t-\sigma ^{2}t^{2}/2)}
Información de Fisher	I ( micras , σ ) = ( 1 / σ 2 0 0 2 / σ 2 ) {\displaystyle {\mathcal {I}}(\mu ,\sigma )={\begin{pmatrix}1/\sigma ^{2}&0\\0&2/\sigma ^{2}\end{pmatrix}}} I ( micras , σ 2 ) = ( 1 / σ 2 0 0 1 / ( 2 σ 4 ) ) {\displaystyle {\mathcal {I}}(\mu ,\sigma ^{2})={\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}}
Divergencia de Kullback-Leibler	1 2 { ( σ 0 σ 1 ) 2 + ( μ 1 − μ 0 ) 2 σ 1 2 − 1 + ln ⁡ σ 1 2 σ 0 2 } {\displaystyle {1 \over 2}\left\{\left({\frac {\sigma _{0}}{\sigma _{1}}}\right)^{2}+{\frac {(\mu _{1}-\mu _{0})^{2}}{\sigma _{1}^{2}}}-1+\ln {\sigma _{1}^{2} \over \sigma _{0}^{2}}\right\}}
Déficit esperado	μ − σ 1 2 π e − ( q p ( X − μ σ ) ) 2 2 1 − p {\displaystyle \mu -\sigma {\frac {{\frac {1}{\sqrt {2\pi }}}e^{\frac {-\left(q_{p}\left({\frac {X-\mu }{\sigma }}\right)\right)^{2}}{2}}}{1-p}}}

Distribución de probabilidad

En teoría de probabilidad y estadística , una distribución normal o distribución gaussiana es un tipo de distribución de probabilidad continua para una variable aleatoria de valor real . La forma general de su función de densidad de probabilidad es El parámetro es la media o esperanza de la distribución (y también su mediana y moda ), mientras que el parámetro es la varianza . La desviación estándar de la distribución es (sigma). Se dice que una variable aleatoria con una distribución gaussiana tiene una distribución normal y se denomina desviación normal . $f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\,.$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\textstyle \sigma }$

Las distribuciones normales son importantes en estadística y se utilizan a menudo en las ciencias naturales y sociales para representar variables aleatorias de valor real cuyas distribuciones no se conocen. ^[2]^[3] Su importancia se debe en parte al teorema del límite central . Este afirma que, en determinadas condiciones, el promedio de muchas muestras (observaciones) de una variable aleatoria con media y varianza finitas es en sí mismo una variable aleatoria, cuya distribución converge a una distribución normal a medida que aumenta el número de muestras. Por lo tanto, las cantidades físicas que se espera que sean la suma de muchos procesos independientes, como los errores de medición , a menudo tienen distribuciones que son casi normales. ^[4]

Además, las distribuciones gaussianas tienen algunas propiedades únicas que son valiosas en los estudios analíticos. Por ejemplo, cualquier combinación lineal de un conjunto fijo de desviaciones normales independientes es una desviación normal. Muchos resultados y métodos, como la propagación de la incertidumbre y el ajuste de parámetros por mínimos cuadrados ^[5] , se pueden derivar analíticamente en forma explícita cuando las variables relevantes se distribuyen normalmente.

A veces, a una distribución normal se la denomina informalmente curva de campana . ^[6] Sin embargo, muchas otras distribuciones tienen forma de campana (como la distribución de Cauchy , la t de Student y las distribuciones logísticas ). (Para conocer otros nombres, consulte Denominación ).

La distribución de probabilidad univariante se generaliza para los vectores en la distribución normal multivariante y para las matrices en la distribución normal matricial .

Definiciones

Distribución normal estándar

El caso más simple de una distribución normal se conoce como distribución normal estándar o distribución normal unitaria . Este es un caso especial cuando y , y se describe mediante esta función de densidad de probabilidad (o densidad): La variable tiene una media de 0 y una varianza y desviación estándar de 1. La densidad tiene su pico en y puntos de inflexión en y . ${\textstyle \mu =0}$ ${\textstyle \sigma ^{2}=1}$ $\varphi (z)={\frac {e^{\frac {-z^{2}}{2}}}{\sqrt {2\pi }}}\,.$ ${\textstyle z}$ ${\textstyle \varphi (z)}$ ${\textstyle {\frac {1}{\sqrt {2\pi }}}}$ ${\textstyle z=0}$ ${\textstyle z=+1}$ ${\textstyle z=-1}$

Aunque la densidad anterior se conoce más comúnmente como la normal estándar, algunos autores han utilizado ese término para describir otras versiones de la distribución normal. Carl Friedrich Gauss , por ejemplo, una vez definió la normal estándar como que tiene una varianza de ⁠ ⁠ , y Stephen Stigler ^[7] una vez definió la normal estándar como que tiene una forma funcional simple y una varianza de $\varphi (z)={\frac {e^{-z^{2}}}{\sqrt {\pi }}},$ ${\frac {1}{2}}$ $\varphi (z)=e^{-\pi z^{2}},$ ${\textstyle \sigma ^{2}={\frac {1}{2\pi }}.}$

Distribución normal general

Toda distribución normal es una versión de la distribución normal estándar, cuyo dominio ha sido ampliado por un factor (la desviación estándar) y luego traducido por (el valor medio): ${\textstyle \sigma }$ ${\textstyle \mu }$

$f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sigma }}\varphi \left({\frac {x-\mu }{\sigma }}\right)\,.$

La densidad de probabilidad debe escalarse de modo que la integral siga siendo 1. ${\textstyle 1/\sigma }$

Si es una desviación normal estándar , entonces tendrá una distribución normal con valor esperado y desviación estándar . Esto es equivalente a decir que la distribución normal estándar se puede escalar/estirar por un factor de y desplazar por para producir una distribución normal diferente, llamada . Por el contrario, si es una desviación normal con parámetros y , entonces esta distribución se puede volver a escalar y desplazar mediante la fórmula para convertirla en la distribución normal estándar. Esta variante también se denomina forma estandarizada de . ${\textstyle Z}$ ${\textstyle X=\sigma Z+\mu }$ ${\textstyle \mu }$ ${\textstyle \sigma }$ ${\textstyle Z}$ ${\textstyle \sigma }$ ${\textstyle \mu }$ ${\textstyle X}$ ${\textstyle X}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\textstyle X}$ ${\textstyle Z=(X-\mu )/\sigma }$ ${\textstyle X}$

Notación

La densidad de probabilidad de la distribución gaussiana estándar (distribución normal estándar, con media cero y varianza unitaria) se denota a menudo con la letra griega ( phi ). ^[8] La forma alternativa de la letra griega phi, , también se utiliza con bastante frecuencia. ${\textstyle \phi }$ ${\textstyle \varphi }$

La distribución normal a menudo se denomina o . ^[9] Por lo tanto, cuando una variable aleatoria se distribuye normalmente con media y desviación estándar , se puede escribir ${\textstyle N(\mu ,\sigma ^{2})}$ ${\textstyle {\mathcal {N}}(\mu ,\sigma ^{2})}$ ${\textstyle X}$ ${\textstyle \mu }$ ${\textstyle \sigma }$

$X\sim {\mathcal {N}}(\mu ,\sigma ^{2}).$

Parametrizaciones alternativas

Algunos autores recomiendan utilizar la precisión como parámetro que define el ancho de la distribución, en lugar de la desviación estándar o la varianza . La precisión se define normalmente como el recíproco de la varianza, . ^[10] La fórmula para la distribución se convierte entonces en ${\textstyle \tau }$ ${\textstyle \sigma }$ ${\textstyle \sigma ^{2}}$ ${\textstyle 1/\sigma ^{2}}$

$f(x)={\sqrt {\frac {\tau }{2\pi }}}e^{-\tau (x-\mu )^{2}/2}.$

Se afirma que esta elección tiene ventajas en los cálculos numéricos cuando está muy cerca de cero y simplifica las fórmulas en algunos contextos, como en la inferencia bayesiana de variables con distribución normal multivariada . ${\textstyle \sigma }$

Alternativamente, el recíproco de la desviación estándar podría definirse como la precisión , en cuyo caso la expresión de la distribución normal se convierte en ${\textstyle \tau '=1/\sigma }$

$f(x)={\frac {\tau '}{\sqrt {2\pi }}}e^{-(\tau ')^{2}(x-\mu )^{2}/2}.$

Según Stigler, esta formulación es ventajosa debido a una fórmula mucho más simple y fácil de recordar, y a fórmulas aproximadas simples para los cuantiles de la distribución.

Las distribuciones normales forman una familia exponencial con parámetros naturales y , y estadísticas naturales x y x ² . Los parámetros de expectativa dual para la distribución normal son η ₁ = μ y η ₂ = μ ² + σ ² . ${\textstyle \textstyle \theta _{1}={\frac {\mu }{\sigma ^{2}}}}$ ${\textstyle \textstyle \theta _{2}={\frac {-1}{2\sigma ^{2}}}}$

Función de distribución acumulativa

La función de distribución acumulativa (CDF) de la distribución normal estándar, usualmente denotada con la letra griega mayúscula , es la integral ${\textstyle \Phi }$

$\Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-t^{2}/2}\,dt\,.$

Función de error

La función de error relacionada da la probabilidad de una variable aleatoria, con distribución normal de media 0 y varianza 1/2 dentro del rango . Es decir: ${\textstyle \operatorname {erf} (x)}$ ${\textstyle [-x,x]}$

$\operatorname {erf} (x)={\frac {1}{\sqrt {\pi }}}\int _{-x}^{x}e^{-t^{2}}\,dt={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt\,.$

Estas integrales no se pueden expresar en términos de funciones elementales y, a menudo, se dice que son funciones especiales . Sin embargo, se conocen muchas aproximaciones numéricas; consulte más información a continuación.

Las dos funciones están estrechamente relacionadas, a saber:

$\Phi (x)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {2}}}\right)\right]\,.$

Para una distribución normal genérica con densidad , media y varianza , la función de distribución acumulativa es ${\textstyle f}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$

$F(x)=\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]\,.$

El complemento de la función de distribución acumulativa normal estándar, , se suele denominar función Q , especialmente en textos de ingeniería. ^[11]^[12] Da la probabilidad de que el valor de una variable aleatoria normal estándar supere a : . Otras definiciones de la función -, todas las cuales son transformaciones simples de , también se utilizan ocasionalmente. ^[13] ${\textstyle Q(x)=1-\Phi (x)}$ ${\textstyle X}$ ${\textstyle x}$ ${\textstyle P(X>x)}$ ${\textstyle Q}$ ${\textstyle \Phi }$

La gráfica de la función de distribución acumulativa normal estándar tiene simetría rotacional doble alrededor del punto (0,1/2); es decir, . Su antiderivada (integral indefinida) se puede expresar de la siguiente manera: ${\textstyle \Phi }$ ${\textstyle \Phi (-x)=1-\Phi (x)}$ $\int \Phi (x)\,dx=x\Phi (x)+\varphi (x)+C.$

La función de distribución acumulativa de la distribución normal estándar se puede ampliar mediante la integración por partes en una serie:

$\Phi (x)={\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\cdot e^{-x^{2}/2}\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+\cdots +{\frac {x^{2n+1}}{(2n+1)!!}}+\cdots \right]\,.$

donde denota el factorial doble . ${\textstyle !!}$

También se puede derivar una expansión asintótica de la función de distribución acumulativa para valores grandes de x mediante la integración por partes. Para obtener más información, consulte Función de error#Expansión asintótica . ^[14]

Se puede encontrar una aproximación rápida a la función de distribución acumulativa de la distribución normal estándar utilizando una aproximación de la serie de Taylor:

$\Phi (x)\approx {\frac {1}{2}}+{\frac {1}{\sqrt {2\pi }}}\sum _{k=0}^{n}{\frac {(-1)^{k}x^{(2k+1)}}{2^{k}k!(2k+1)}}\,.$

Cálculo recursivo con desarrollo de la serie de Taylor

La naturaleza recursiva de la familia de derivadas se puede utilizar para construir fácilmente una expansión de la serie de Taylor rápidamente convergente utilizando entradas recursivas sobre cualquier punto de valor conocido de la distribución : ${\textstyle e^{ax^{2}}}$ ${\textstyle \Phi (x_{0})}$

$\Phi (x)=\sum _{n=0}^{\infty }{\frac {\Phi ^{(n)}(x_{0})}{n!}}(x-x_{0})^{n}\,,$

dónde:

${\begin{aligned}\Phi ^{(0)}(x_{0})&={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x_{0}}e^{-t^{2}/2}\,dt\\\Phi ^{(1)}(x_{0})&={\frac {1}{\sqrt {2\pi }}}e^{-x_{0}^{2}/2}\\\Phi ^{(n)}(x_{0})&=-\left(x_{0}\Phi ^{(n-1)}(x_{0})+(n-2)\Phi ^{(n-2)}(x_{0})\right),&n\geq 2\,.\end{aligned}}$

Utilizando la serie de Taylor y el método de Newton para la función inversa

Una aplicación de la expansión de la serie de Taylor anterior es utilizar el método de Newton para invertir el cálculo. Es decir, si tenemos un valor para la función de distribución acumulativa , , pero no conocemos la x necesaria para obtener , podemos utilizar el método de Newton para encontrar x, y utilizar la expansión de la serie de Taylor anterior para minimizar el número de cálculos. El método de Newton es ideal para resolver este problema porque la primera derivada de , que es una integral de la distribución estándar normal, es la distribución estándar normal y está disponible para su uso en la solución del método de Newton. ${\textstyle \Phi (x)}$ ${\textstyle \Phi (x)}$ ${\textstyle \Phi (x)}$

Para resolver, seleccione una solución aproximada conocida, , para el . deseado puede ser un valor de una tabla de distribución o una estimación inteligente seguida de un cálculo de utilizando cualquier medio deseado para calcular. Utilice este valor de y la expansión de la serie de Taylor anterior para minimizar los cálculos. ${\textstyle x_{0}}$ ${\textstyle \Phi (x)}$ ${\textstyle x_{0}}$ ${\textstyle \Phi (x_{0})}$ ${\textstyle x_{0}}$

Repita el siguiente proceso hasta que la diferencia entre el calculado y el deseado , que llamaremos , esté por debajo de un error aceptablemente pequeño, como 10 ⁻⁵ , 10 ⁻¹⁵ , etc.: ${\textstyle \Phi (x_{n})}$ ${\textstyle \Phi }$ ${\textstyle \Phi ({\text{desired}})}$

$x_{n+1}=x_{n}-{\frac {\Phi (x_{n},x_{0},\Phi (x_{0}))-\Phi ({\text{desired}})}{\Phi '(x_{n})}}\,,$

dónde

{\textstyle \Phi (x,x_{0},\Phi (x_{0}))}

es la solución de una serie de Taylor usando y

{\textstyle \Phi (x)}

{\textstyle x_{0}}

{\textstyle \Phi (x_{0})}

$\Phi '(x_{n})={\frac {1}{\sqrt {2\pi }}}e^{-x_{n}^{2}/2}\,.$

Cuando los cálculos repetidos convergen a un error inferior al valor aceptablemente pequeño elegido, x será el valor necesario para obtener a del valor deseado, . ${\textstyle \Phi (x)}$ ${\textstyle \Phi ({\text{desired}})}$

Desviación estándar y cobertura

Alrededor del 68% de los valores extraídos de una distribución normal están dentro de una desviación estándar σ de la media; alrededor del 95% de los valores se encuentran dentro de dos desviaciones estándar; y alrededor del 99,7% están dentro de tres desviaciones estándar. ^[6] Este hecho se conoce como la regla 68-95-99,7 (empírica) o la regla de 3 sigma .

Más precisamente, la probabilidad de que una desviación normal se encuentre en el rango entre y está dada por Para 12 dígitos significativos, los valores para son: ${\textstyle \mu -n\sigma }$ ${\textstyle \mu +n\sigma }$ $F(\mu +n\sigma )-F(\mu -n\sigma )=\Phi (n)-\Phi (-n)=\operatorname {erf} \left({\frac {n}{\sqrt {2}}}\right).$ ${\textstyle n=1,2,\ldots ,6}$

{\textstyle n}

{\textstyle p=F(\mu +n\sigma )-F(\mu -n\sigma )}

{\textstyle 1-p}

{\textstyle {\text{or }}1{\text{ in }}(1-p)}

OEIS

1

0,682 689 492 137

0,317 310 507 863

3	.151 487 187 53

Norma OEIS : A178647

2

0,954 499 736 104

0,045 500 263 896

21	.977 894 5080

Norma OEIS : A110894

3

0,997 300 203 937

0,002 699 796 063

370	.398 347 345

Norma OEIS : A270712

4

0,999 936 657 516

0.000 063 342 484

15 787

.192 7673

5

0,999 999 426 697

0.000 000 573 303

1 744 277

.893 62

6

0,999 999 998 027

0.000 000 001 973

506 797 345

.897

Para valores grandes , se puede utilizar la aproximación . ${\textstyle n}$ ${\textstyle 1-p\approx {\frac {e^{-n^{2}/2}}{n{\sqrt {\pi /2}}}}}$

Función cuantil

La función cuantil de una distribución es la inversa de la función de distribución acumulativa. La función cuantil de la distribución normal estándar se denomina función probit y se puede expresar en términos de la función de error inversa : Para una variable aleatoria normal con media y varianza , la función cuantil es El cuantil de la distribución normal estándar se denota comúnmente como . Estos valores se utilizan en pruebas de hipótesis , construcción de intervalos de confianza y gráficos Q-Q . Una variable aleatoria normal excederá con probabilidad , y quedará fuera del intervalo con probabilidad . En particular, el cuantil es 1,96 ; por lo tanto, una variable aleatoria normal quedará fuera del intervalo solo en el 5% de los casos. $\Phi ^{-1}(p)={\sqrt {2}}\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ $F^{-1}(p)=\mu +\sigma \Phi ^{-1}(p)=\mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2p-1),\quad p\in (0,1).$ ${\textstyle \Phi ^{-1}(p)}$ ${\textstyle z_{p}}$ ${\textstyle X}$ ${\textstyle \mu +z_{p}\sigma }$ ${\textstyle 1-p}$ ${\textstyle \mu \pm z_{p}\sigma }$ ${\textstyle 2(1-p)}$ ${\textstyle z_{0.975}}$ ${\textstyle \mu \pm 1.96\sigma }$

La siguiente tabla muestra el cuartil que se encontrará en el rango con una probabilidad especificada . Estos valores son útiles para determinar el intervalo de tolerancia para promedios de muestra y otros estimadores estadísticos con distribuciones normales (o asintóticamente normales). ^[15] La siguiente tabla muestra , no como se definió anteriormente. ${\textstyle z_{p}}$ ${\textstyle X}$ ${\textstyle \mu \pm z_{p}\sigma }$ ${\textstyle p}$ ${\textstyle {\sqrt {2}}\operatorname {erf} ^{-1}(p)=\Phi ^{-1}\left({\frac {p+1}{2}}\right)}$ ${\textstyle \Phi ^{-1}(p)}$

${\textstyle p}$	${\textstyle z_{p}}$	${\textstyle p}$	${\textstyle z_{p}}$
0,80	1.281 551 565 545	0,999	3.290 526 731 492
0,90	1.644 853 626 951	0,9999	3.890 591 886 413
0,95	1.959 963 984 540	0,99999	4.417 173 413 469
0,98	2.326 347 874 041	0,999999	4.891 638 475 699
0,99	2.575 829 303 549	0,9999999	5.326 723 886 384
0,995	2.807 033 768 344	0,99999999	5.730 728 868 236
0,998	3.090 232 306 168	0,999999999	6.109 410 204 869

Para números pequeños , la función cuantil tiene la expansión asintótica útil ^[^{cita requerida}^] ${\textstyle p}$ ${\textstyle \Phi ^{-1}(p)=-{\sqrt {\ln {\frac {1}{p^{2}}}-\ln \ln {\frac {1}{p^{2}}}-\ln(2\pi )}}+{\mathcal {o}}(1).}$

Propiedades

La distribución normal es la única distribución cuyos cumulantes más allá de los dos primeros (es decir, distintos de la media y la varianza ) son cero. También es la distribución continua con la entropía máxima para una media y varianza especificadas. ^[16]^[17] Geary ha demostrado, suponiendo que la media y la varianza son finitas, que la distribución normal es la única distribución donde la media y la varianza calculadas a partir de un conjunto de valores extraídos independientes son independientes entre sí. ^[18]^[19]

La distribución normal es una subclase de las distribuciones elípticas . La distribución normal es simétrica respecto de su media y no es cero en toda la línea real. Como tal, puede no ser un modelo adecuado para variables que son inherentemente positivas o fuertemente sesgadas, como el peso de una persona o el precio de una acción . Dichas variables pueden describirse mejor mediante otras distribuciones, como la distribución log-normal o la distribución de Pareto .

El valor de la densidad normal es prácticamente cero cuando el valor se encuentra a más de unas pocas desviaciones estándar de la media (por ejemplo, una dispersión de tres desviaciones estándar cubre toda la distribución total, excepto el 0,27%). Por lo tanto, puede no ser un modelo apropiado cuando se espera una fracción significativa de valores atípicos (valores que se encuentran a muchas desviaciones estándar de la media) y los mínimos cuadrados y otros métodos de inferencia estadística que son óptimos para las variables distribuidas normalmente suelen volverse muy poco confiables cuando se aplican a esos datos. En esos casos, se debe suponer una distribución de colas más pesadas y aplicar los métodos de inferencia estadística robustos adecuados . ${\textstyle x}$

La distribución gaussiana pertenece a la familia de distribuciones estables que son las que atraen las sumas de distribuciones independientes, idénticamente distribuidas, independientemente de que la media o la varianza sean finitas o no. A excepción de la gaussiana, que es un caso límite, todas las distribuciones estables tienen colas pesadas y varianza infinita. Es una de las pocas distribuciones que son estables y que tienen funciones de densidad de probabilidad que se pueden expresar analíticamente, las otras son la distribución de Cauchy y la distribución de Lévy .

Simetrías y derivadas

La distribución normal con densidad (media y varianza ) tiene las siguientes propiedades: ${\textstyle f(x)}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}>0}$

Es simétrica alrededor del punto que es al mismo tiempo la moda , la mediana y la media de la distribución. ^[20] ${\textstyle x=\mu ,}$
Es unimodal : su primera derivada es positiva para negativa para y cero sólo en ${\textstyle x<\mu ,}$ ${\textstyle x>\mu ,}$ ${\textstyle x=\mu .}$
El área delimitada por la curva y el eje es la unidad (es decir, igual a uno). ${\textstyle x}$
Su primera derivada es ${\textstyle f'(x)=-{\frac {x-\mu }{\sigma ^{2}}}f(x).}$
Su segunda derivada es ${\textstyle f''(x)={\frac {(x-\mu )^{2}-\sigma ^{2}}{\sigma ^{4}}}f(x).}$
Su densidad tiene dos puntos de inflexión (donde la segunda derivada de es cero y cambia de signo), ubicados a una desviación estándar de la media, es decir en y ^[20] ${\textstyle f}$ ${\textstyle x=\mu -\sigma }$ ${\textstyle x=\mu +\sigma .}$
Su densidad es logarítmica-cóncava . ^[20]
Su densidad es infinitamente diferenciable , de hecho supersuave , de orden 2. ^[21]

Además, la densidad de la distribución normal estándar (es decir, y ) también tiene las siguientes propiedades: ${\textstyle \varphi }$ ${\textstyle \mu =0}$ ${\textstyle \sigma =1}$

Su primera derivada es ${\textstyle \varphi '(x)=-x\varphi (x).}$
Su segunda derivada es ${\textstyle \varphi ''(x)=(x^{2}-1)\varphi (x)}$
De manera más general, su derivada $n-$ ésima es donde es el $n -ésimo$ polinomio de Hermite (probabilista) . ^[22] ${\textstyle \varphi ^{(n)}(x)=(-1)^{n}\operatorname {He} _{n}(x)\varphi (x),}$ ${\textstyle \operatorname {He} _{n}(x)}$
La probabilidad de que una variable distribuida normalmente con y conocidos esté en un conjunto particular, se puede calcular utilizando el hecho de que la fracción tiene una distribución normal estándar. ${\textstyle X}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\textstyle Z=(X-\mu )/\sigma }$

Momentos

Los momentos simples y absolutos de una variable son los valores esperados de y , respectivamente. Si el valor esperado de es cero, estos parámetros se denominan momentos centrales; de lo contrario, estos parámetros se denominan momentos no centrales. Por lo general, solo nos interesan los momentos con orden entero . ${\textstyle X}$ ${\textstyle X^{p}}$ ${\textstyle |X|^{p}}$ ${\textstyle \mu }$ ${\textstyle X}$ ${\textstyle \ p}$

Si tiene una distribución normal, los momentos no centrales existen y son finitos para cualquier número cuya parte real sea mayor que −1. Para cualquier entero no negativo , los momentos centrales simples son: ^[23] Aquí denota el factorial doble , es decir, el producto de todos los números de a 1 que tienen la misma paridad que ${\textstyle X}$ ${\textstyle p}$ ${\textstyle p}$ $\operatorname {E} \left[(X-\mu )^{p}\right]={\begin{cases}0&{\text{if }}p{\text{ is odd,}}\\\sigma ^{p}(p-1)!!&{\text{if }}p{\text{ is even.}}\end{cases}}$ ${\textstyle n!!}$ ${\textstyle n}$ ${\textstyle n.}$

Los momentos absolutos centrales coinciden con los momentos simples para todos los órdenes pares, pero son distintos de cero para los órdenes impares. Para cualquier entero no negativo ${\textstyle p,}$

${\begin{aligned}\operatorname {E} \left[|X-\mu |^{p}\right]&=\sigma ^{p}(p-1)!!\cdot {\begin{cases}{\sqrt {\frac {2}{\pi }}}&{\text{if }}p{\text{ is odd}}\\1&{\text{if }}p{\text{ is even}}\end{cases}}\\&=\sigma ^{p}\cdot {\frac {2^{p/2}\Gamma \left({\frac {p+1}{2}}\right)}{\sqrt {\pi }}}.\end{aligned}}$ La última fórmula es válida también para cualquier número no entero. Cuando la media de los momentos simples y absolutos se pueden expresar en términos de funciones hipergeométricas confluentes y ^[24] ${\textstyle p>-1.}$ ${\textstyle \mu \neq 0,}$ ${\textstyle {}_{1}F_{1}}$ ${\textstyle U.}$

${\begin{aligned}\operatorname {E} \left[X^{p}\right]&=\sigma ^{p}\cdot (-i{\sqrt {2}})^{p}U\left(-{\frac {p}{2}},{\frac {1}{2}},-{\frac {1}{2}}\left({\frac {\mu }{\sigma }}\right)^{2}\right),\\\operatorname {E} \left[|X|^{p}\right]&=\sigma ^{p}\cdot 2^{p/2}{\frac {\Gamma \left({\frac {1+p}{2}}\right)}{\sqrt {\pi }}}{}_{1}F_{1}\left(-{\frac {p}{2}},{\frac {1}{2}},-{\frac {1}{2}}\left({\frac {\mu }{\sigma }}\right)^{2}\right).\end{aligned}}$

Estas expresiones siguen siendo válidas incluso si no es un número entero. Véase también polinomios de Hermite generalizados . ${\textstyle p}$

Orden	Momento no central	Momento central
1	${\textstyle \mu }$	${\textstyle 0}$
2	${\textstyle \mu ^{2}+\sigma ^{2}}$	${\textstyle \sigma ^{2}}$
3	${\textstyle \mu ^{3}+3\mu \sigma ^{2}}$	${\textstyle 0}$
4	${\textstyle \mu ^{4}+6\mu ^{2}\sigma ^{2}+3\sigma ^{4}}$	${\textstyle 3\sigma ^{4}}$
5	${\textstyle \mu ^{5}+10\mu ^{3}\sigma ^{2}+15\mu \sigma ^{4}}$	${\textstyle 0}$
6	${\textstyle \mu ^{6}+15\mu ^{4}\sigma ^{2}+45\mu ^{2}\sigma ^{4}+15\sigma ^{6}}$	${\textstyle 15\sigma ^{6}}$
7	${\textstyle \mu ^{7}+21\mu ^{5}\sigma ^{2}+105\mu ^{3}\sigma ^{4}+105\mu \sigma ^{6}}$	${\textstyle 0}$
8	${\textstyle \mu ^{8}+28\mu ^{6}\sigma ^{2}+210\mu ^{4}\sigma ^{4}+420\mu ^{2}\sigma ^{6}+105\sigma ^{8}}$	${\textstyle 105\sigma ^{8}}$

La esperanza de condicionada al evento que se encuentra en un intervalo está dada por donde y respectivamente son la densidad y la función de distribución acumulada de . Esto se conoce como el coeficiente de Mills inverso . Tenga en cuenta que anteriormente, se utiliza la densidad de en lugar de la densidad normal estándar como en el coeficiente de Mills inverso, por lo que aquí tenemos en lugar de . ${\textstyle X}$ ${\textstyle X}$ ${\textstyle [a,b]}$ $\operatorname {E} \left[X\mid a<X<b\right]=\mu -\sigma ^{2}{\frac {f(b)-f(a)}{F(b)-F(a)}}\,,$ ${\textstyle f}$ ${\textstyle F}$ ${\textstyle X}$ ${\textstyle b=\infty }$ ${\textstyle f}$ ${\textstyle X}$ ${\textstyle \sigma ^{2}}$ ${\textstyle \sigma }$

Transformada de Fourier y función característica

La transformada de Fourier de una densidad normal con media y varianza es ^[25] ${\textstyle f}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$

${\hat {f}}(t)=\int _{-\infty }^{\infty }f(x)e^{-itx}\,dx=e^{-i\mu t}e^{-{\frac {1}{2}}(\sigma t)^{2}}\,,$

donde es la unidad imaginaria . Si la media , el primer factor es 1, y la transformada de Fourier es, además de un factor constante, una densidad normal en el dominio de la frecuencia , con media 0 y varianza . En particular, la distribución normal estándar es una función propia de la transformada de Fourier. ${\textstyle i}$ ${\textstyle \mu =0}$ ${\textstyle 1/\sigma ^{2}}$ ${\textstyle \varphi }$

En teoría de la probabilidad, la transformada de Fourier de la distribución de probabilidad de una variable aleatoria de valor real está estrechamente relacionada con la función característica de esa variable, que se define como el valor esperado de , en función de la variable real (el parámetro de frecuencia de la transformada de Fourier). Esta definición se puede extender analíticamente a una variable de valor complejo . ^[26] La relación entre ambas es: ${\textstyle X}$ ${\textstyle \varphi _{X}(t)}$ ${\textstyle e^{itX}}$ ${\textstyle t}$ ${\textstyle t}$ $\varphi _{X}(t)={\hat {f}}(-t)\,.$

Funciones generadoras de momentos y cumulantes

La función generadora de momentos de una variable aleatoria real es el valor esperado de , en función del parámetro real . Para una distribución normal con densidad , media y varianza , la función generadora de momentos existe y es igual a ${\textstyle X}$ ${\textstyle e^{tX}}$ ${\textstyle t}$ ${\textstyle f}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$

$M(t)=\operatorname {E} \left[e^{tX}\right]={\hat {f}}(it)=e^{\mu t}e^{\sigma ^{2}t^{2}/2}\,.$ Para cualquier ⁠ ⁠ $k$ , el coeficiente de ⁠ ⁠ $t^{k}/k!$ en la función generadora de momentos (expresada como una serie de potencia exponencial en ⁠ ⁠ $t$ ) es el valor esperado de la distribución normal ⁠ ⁠ $E[X^{k}]$ .

La función generadora cumulante es el logaritmo de la función generadora de momentos, es decir

$g(t)=\ln M(t)=\mu t+{\tfrac {1}{2}}\sigma ^{2}t^{2}\,.$

Los coeficientes de esta serie de potencias exponenciales definen los cumulantes, pero como se trata de un polinomio cuadrático en ⁠ ⁠ $t$ , solo los dos primeros cumulantes son distintos de cero, es decir, la media y la varianza ⁠ ⁠ . ${\textstyle \mu }$ $\sigma ^{2}$

Algunos autores prefieren trabajar con la función característica $E[e itX] = e iμt - σ 2 t 2 /2$ y $ln E[e itX] = iμt - ⁠ 1 / 2 ⁠ σ2t2$ . $$ $$ $$

Operador y clase Stein

Dentro del método de Stein, el operador de Stein y la clase de una variable aleatoria son y la clase de todas las funciones absolutamente continuas . ${\textstyle X\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$ ${\textstyle {\mathcal {A}}f(x)=\sigma ^{2}f'(x)-(x-\mu )f(x)}$ ${\textstyle {\mathcal {F}}}$ ${\textstyle f:\mathbb {R} \to \mathbb {R} {\mbox{ such that }}\mathbb {E} [|f'(X)|]<\infty }$

Límite de varianza cero

En el límite cuando tiende a cero, la densidad de probabilidad tiende eventualmente a cero en cualquier , pero crece sin límite si , mientras que su integral permanece igual a 1. Por lo tanto, la distribución normal no puede definirse como una función ordinaria cuando . ${\textstyle \sigma ^{2}}$ ${\textstyle f(x)}$ ${\textstyle x\neq \mu }$ ${\textstyle x=\mu }$ ${\textstyle \sigma ^{2}=0}$

Sin embargo, se puede definir la distribución normal con varianza cero como una función generalizada ; específicamente, como una función delta de Dirac traducida por la media , es decir Su función de distribución acumulativa es entonces la función escalón de Heaviside traducida por la media , es decir ${\textstyle \delta }$ ${\textstyle \mu }$ ${\textstyle f(x)=\delta (x-\mu ).}$ ${\textstyle \mu }$ $F(x)={\begin{cases}0&{\text{if }}x<\mu \\1&{\text{if }}x\geq \mu \,.\end{cases}}$

Entropía máxima

De todas las distribuciones de probabilidad sobre los números reales con una media finita especificada y una varianza finita , la distribución normal es la que tiene una entropía máxima . ^[27] Para ver esto, sea una variable aleatoria continua con densidad de probabilidad . La entropía de se define como ^[28]^[29]^[30] ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\textstyle N(\mu ,\sigma ^{2})}$ ${\textstyle X}$ ${\textstyle f(x)}$ ${\textstyle X}$ $H(X)=-\int _{-\infty }^{\infty }f(x)\ln f(x)\,dx\,,$

donde se entiende que es cero siempre que . Esta función se puede maximizar, sujeta a las restricciones de que la distribución esté correctamente normalizada y tenga una media y varianza especificadas, mediante el uso del cálculo variacional . Se define una función con tres multiplicadores de Lagrange : ${\textstyle f(x)\log f(x)}$ ${\textstyle f(x)=0}$

$L=-\int _{-\infty }^{\infty }f(x)\ln f(x)\,dx-\lambda _{0}\left(1-\int _{-\infty }^{\infty }f(x)\,dx\right)-\lambda _{1}\left(\mu -\int _{-\infty }^{\infty }f(x)x\,dx\right)-\lambda _{2}\left(\sigma ^{2}-\int _{-\infty }^{\infty }f(x)(x-\mu )^{2}\,dx\right)\,.$

Con máxima entropía, una pequeña variación de producirá una variación de que es igual a 0: ${\textstyle \delta f(x)}$ ${\textstyle f(x)}$ ${\textstyle \delta L}$ ${\textstyle L}$

$0=\delta L=\int _{-\infty }^{\infty }\delta f(x)\left(-\ln f(x)-1+\lambda _{0}+\lambda _{1}x+\lambda _{2}(x-\mu )^{2}\right)\,dx\,.$

Dado que esto debe ser válido para cualquier α pequeño , el factor que se multiplica debe ser cero, y al resolver se obtiene: ${\textstyle \delta f(x)}$ ${\textstyle \delta f(x)}$ ${\textstyle f(x)}$

$f(x)=\exp \left(-1+\lambda _{0}+\lambda _{1}x+\lambda _{2}(x-\mu )^{2}\right)\,.$

Las restricciones de Lagrange que están correctamente normalizadas y tienen la media y varianza especificadas se satisfacen si y solo si , , y se eligen de modo que La entropía de una distribución normal es igual a que es independiente de la media . ${\textstyle f(x)}$ ${\textstyle \lambda _{0}}$ ${\textstyle \lambda _{1}}$ ${\textstyle \lambda _{2}}$ $f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\,.$ ${\textstyle X\sim N(\mu ,\sigma ^{2})}$ $H(X)={\tfrac {1}{2}}(1+\ln 2\sigma ^{2}\pi )\,,$ ${\textstyle \mu }$

Otras propiedades

Si la función característica de alguna variable aleatoria es de la forma en un entorno de cero, donde es un polinomio , entonces el teorema de Marcinkiewicz (llamado así por Józef Marcinkiewicz ) afirma que puede ser como máximo un polinomio cuadrático y, por lo tanto, es una variable aleatoria normal. ^{[31] La consecuencia de este resultado es que la distribución normal es la única distribución con un número finito (dos) de}cumulantes distintos de cero . ${\textstyle \phi _{X}}$ ${\textstyle X}$ ${\textstyle \phi _{X}(t)=\exp Q(t)}$ ${\textstyle Q(t)}$ ${\textstyle Q}$ ${\textstyle X}$
Si y son conjuntamente normales y no correlacionados , entonces son independientes . El requisito de que y sean conjuntamente normales es esencial; sin él la propiedad no se cumple. ^[32]^[33]^[prueba] Para las variables aleatorias no normales, la no correlación no implica independencia. ${\textstyle X}$ ${\textstyle Y}$ ${\textstyle X}$ ${\textstyle Y}$
La divergencia de Kullback-Leibler de una distribución normal respecto de otra está dada por: ^[34] La distancia de Hellinger entre las mismas distribuciones es igual a ${\textstyle X_{1}\sim N(\mu _{1},\sigma _{1}^{2})}$ ${\textstyle X_{2}\sim N(\mu _{2},\sigma _{2}^{2})}$ $D_{\mathrm {KL} }(X_{1}\parallel X_{2})={\frac {(\mu _{1}-\mu _{2})^{2}}{2\sigma _{2}^{2}}}+{\frac {1}{2}}\left({\frac {\sigma _{1}^{2}}{\sigma _{2}^{2}}}-1-\ln {\frac {\sigma _{1}^{2}}{\sigma _{2}^{2}}}\right)$ $H^{2}(X_{1},X_{2})=1-{\sqrt {\frac {2\sigma _{1}\sigma _{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}}}\exp \left(-{\frac {1}{4}}{\frac {(\mu _{1}-\mu _{2})^{2}}{\sigma _{1}^{2}+\sigma _{2}^{2}}}\right)$
La matriz de información de Fisher para una distribución normal con respecto a y es diagonal y toma la forma ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\mathcal {I}}(\mu ,\sigma ^{2})={\begin{pmatrix}{\frac {1}{\sigma ^{2}}}&0\\0&{\frac {1}{2\sigma ^{4}}}\end{pmatrix}}$
La distribución conjugada anterior de la media de una distribución normal es otra distribución normal. ^[35] Específicamente, si son iid y la distribución anterior es , entonces la distribución posterior para el estimador de será ${\textstyle x_{1},\ldots ,x_{n}}$ ${\textstyle \sim N(\mu ,\sigma ^{2})}$ ${\textstyle \mu \sim N(\mu _{0},\sigma _{0}^{2})}$ ${\textstyle \mu }$ $\mu \mid x_{1},\ldots ,x_{n}\sim {\mathcal {N}}\left({\frac {{\frac {\sigma ^{2}}{n}}\mu _{0}+\sigma _{0}^{2}{\bar {x}}}{{\frac {\sigma ^{2}}{n}}+\sigma _{0}^{2}}},\left({\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}\right)^{-1}\right)$
La familia de distribuciones normales no solo forma una familia exponencial (EF), sino que de hecho forma una familia exponencial natural (NEF) con función de varianza cuadrática ( NEF-QVF ). Muchas propiedades de las distribuciones normales se generalizan a propiedades de las distribuciones NEF-QVF, distribuciones NEF o distribuciones EF en general. Las distribuciones NEF-QVF comprenden 6 familias, incluidas las distribuciones Poisson, Gamma, binomial y binomial negativa, mientras que muchas de las familias comunes estudiadas en probabilidad y estadística son NEF o EF.
En geometría de la información , la familia de distribuciones normales forma una variedad estadística con curvatura constante . La misma familia es plana con respecto a las conexiones (±1) y . ^[36] ${\textstyle -1}$ ${\textstyle \nabla ^{(e)}}$ ${\textstyle \nabla ^{(m)}}$
Si se distribuyen según , entonces . Nótese que no hay ningún supuesto de independencia. ^[37] ${\textstyle X_{1},\dots ,X_{n}}$ ${\textstyle N(0,\sigma ^{2})}$ ${\textstyle E[\max _{i}X_{i}]\leq \sigma {\sqrt {2\ln n}}}$

Distribuciones relacionadas

Teorema del límite central

A medida que aumenta el número de eventos discretos, la función comienza a parecerse a una distribución normal.

Comparación de funciones de densidad de probabilidad para la suma de dados de 6 caras para mostrar su convergencia a una distribución normal con un aumento de , de acuerdo con el teorema del límite central. En el gráfico inferior derecho, los perfiles suavizados de los gráficos anteriores se reescalan, se superponen y se comparan con una distribución normal (curva negra). ${\textstyle p(k)}$ ${\textstyle n}$ ${\textstyle na}$

El teorema del límite central establece que, en determinadas condiciones (bastante comunes), la suma de muchas variables aleatorias tendrá una distribución aproximadamente normal. Más específicamente, donde son variables aleatorias independientes e idénticamente distribuidas con la misma distribución arbitraria, media y varianza cero y su media está escalada por Entonces, a medida que aumenta, la distribución de probabilidad de tenderá a la distribución normal con media y varianza cero . ${\textstyle X_{1},\ldots ,X_{n}}$ ${\textstyle \sigma ^{2}}$ ${\textstyle Z}$ ${\textstyle {\sqrt {n}}}$ $Z={\sqrt {n}}\left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)$ ${\textstyle n}$ ${\textstyle Z}$ ${\textstyle \sigma ^{2}}$

El teorema puede extenderse a variables que no son independientes y/o no están distribuidas idénticamente si se imponen ciertas restricciones al grado de dependencia y a los momentos de las distribuciones. ${\textstyle (X_{i})}$

Muchas estadísticas de prueba , puntuaciones y estimadores que se encuentran en la práctica contienen sumas de ciertas variables aleatorias, e incluso más estimadores pueden representarse como sumas de variables aleatorias mediante el uso de funciones de influencia . El teorema del límite central implica que esos parámetros estadísticos tendrán distribuciones asintóticamente normales.

El teorema del límite central también implica que ciertas distribuciones pueden aproximarse mediante la distribución normal, por ejemplo:

La distribución binomial es aproximadamente normal con media y varianza grandes y no demasiado cercanas a 0 o 1. ${\textstyle B(n,p)}$ ${\textstyle np}$ ${\textstyle np(1-p)}$ ${\textstyle n}$ ${\textstyle p}$
La distribución de Poisson con parámetro es aproximadamente normal con media y varianza , para valores grandes de . ^[38] ${\textstyle \lambda }$ ${\textstyle \lambda }$ ${\textstyle \lambda }$ ${\textstyle \lambda }$
La distribución de chi-cuadrado es aproximadamente normal con media y varianza , para valores grandes . ${\textstyle \chi ^{2}(k)}$ ${\textstyle k}$ ${\textstyle 2k}$ ${\textstyle k}$
La distribución t de Student es aproximadamente normal con media 0 y varianza 1 cuando es grande. ${\textstyle t(\nu )}$ ${\textstyle \nu }$

La precisión de estas aproximaciones depende del propósito para el que se necesitan y de la tasa de convergencia a la distribución normal. Por lo general, estas aproximaciones son menos precisas en los extremos de la distribución.

El teorema de Berry-Esseen proporciona un límite superior general para el error de aproximación en el teorema del límite central y las expansiones de Edgeworth proporcionan mejoras en la aproximación .

Este teorema también se puede utilizar para justificar la modelización de la suma de muchas fuentes de ruido uniformes como ruido gaussiano . Véase AWGN .

Operaciones y funciones de variables normales

a: Densidad de probabilidad de una función de una variable normal con y . b: Densidad de probabilidad de una función de dos variables normales y , donde , , , , y . c: Mapa de calor de la densidad de probabilidad conjunta de dos funciones de dos variables normales correlacionadas y , donde , , , , y . d: Densidad de probabilidad de una función de 4 variables normales estándar iid. Estas se calculan mediante el método numérico de trazado de rayos. ^[39] ${\textstyle \cos x^{2}}$ ${\textstyle x}$ ${\textstyle \mu =-2}$ ${\textstyle \sigma =3}$ ${\textstyle x^{y}}$ ${\textstyle x}$ ${\textstyle y}$ ${\textstyle \mu _{x}=1}$ ${\textstyle \mu _{y}=2}$ ${\textstyle \sigma _{x}=0.1}$ ${\textstyle \sigma _{y}=0.2}$ ${\textstyle \rho _{xy}=0.8}$ ${\textstyle x}$ ${\textstyle y}$ ${\textstyle \mu _{x}=-2}$ ${\textstyle \mu _{y}=5}$ ${\textstyle \sigma _{x}^{2}=10}$ ${\textstyle \sigma _{y}^{2}=20}$ ${\textstyle \rho _{xy}=0.495}$ ${\textstyle \sum _{i=1}^{4}\vert x_{i}\vert }$

La densidad de probabilidad , la distribución acumulativa y la distribución acumulativa inversa de cualquier función de una o más variables normales independientes o correlacionadas se pueden calcular con el método numérico de trazado de rayos ^[39] (código Matlab). En las siguientes secciones, analizamos algunos casos especiales.

Operaciones sobre una sola variable normal

Si se distribuye normalmente con media y varianza , entonces ${\textstyle X}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$

${\textstyle aX+b}$ , para cualquier número real y , también se distribuye normalmente, con media y varianza . Es decir, la familia de distribuciones normales está cerrada ante transformaciones lineales . ${\textstyle a}$ ${\textstyle b}$ ${\textstyle a\mu +b}$ ${\textstyle a^{2}\sigma ^{2}}$
La exponencial de se distribuye log-normalmente : . ${\textstyle X}$ ${\textstyle e^{X}\sim \ln(N(\mu ,\sigma ^{2}))}$
La sigmoide estándar de tiene una distribución logit-normal : . ${\textstyle X}$ ${\textstyle \sigma (X)\sim P({\mathcal {N}}(\mu ,\,\sigma ^{2}))}$
El valor absoluto de tiene una distribución normal plegada : . Si esto se conoce como distribución seminormal . ${\textstyle X}$ ${\textstyle {\left|X\right|\sim N_{f}(\mu ,\sigma ^{2})}}$ ${\textstyle \mu =0}$
El valor absoluto de los residuos normalizados, , tiene distribución chi con un grado de libertad: . ${\textstyle |X-\mu |/\sigma }$ ${\textstyle |X-\mu |/\sigma \sim \chi _{1}}$
El cuadrado de tiene una distribución chi-cuadrado no central con un grado de libertad: . Si , la distribución se denomina simplemente chi-cuadrado . ${\textstyle X/\sigma }$ ${\textstyle X^{2}/\sigma ^{2}\sim \chi _{1}^{2}(\mu ^{2}/\sigma ^{2})}$ ${\textstyle \mu =0}$
La verosimilitud logarítmica de una variable normal es simplemente el logaritmo de su función de densidad de probabilidad : dado que se trata de un cuadrado escalado y desplazado de una variable normal estándar, se distribuye como una variable chi-cuadrado escalada y desplazada. ${\textstyle x}$ $\ln p(x)=-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}-\ln \left(\sigma {\sqrt {2\pi }}\right).$
La distribución de la variable restringida a un intervalo se denomina distribución normal truncada . ${\textstyle X}$ ${\textstyle [a,b]}$
${\textstyle (X-\mu )^{-2}}$ tiene una distribución de Lévy con ubicación 0 y escala . ${\textstyle \sigma ^{-2}}$

Operaciones sobre dos variables normales independientes

Si y son dos variables aleatorias normales independientes , con medias , y varianzas , , entonces su suma también estará distribuida normalmente, ^[prueba] con media y varianza . ${\textstyle X_{1}}$ ${\textstyle X_{2}}$ ${\textstyle \mu _{1}}$ ${\textstyle \mu _{2}}$ ${\textstyle \sigma _{1}^{2}}$ ${\textstyle \sigma _{2}^{2}}$ ${\textstyle X_{1}+X_{2}}$ ${\textstyle \mu _{1}+\mu _{2}}$ ${\textstyle \sigma _{1}^{2}+\sigma _{2}^{2}}$
En particular, si y son desviaciones normales independientes con media y varianza cero , entonces y también son independientes y se distribuyen normalmente, con media y varianza cero . Este es un caso especial de la identidad de polarización . ^[40] ${\textstyle X}$ ${\textstyle Y}$ ${\textstyle \sigma ^{2}}$ ${\textstyle X+Y}$ ${\textstyle X-Y}$ ${\textstyle 2\sigma ^{2}}$
Si , son dos desviaciones normales independientes con media y varianza , y , son números reales arbitrarios, entonces la variable también se distribuye normalmente con media y varianza . De ello se deduce que la distribución normal es estable (con exponente ). ${\textstyle X_{1}}$ ${\textstyle X_{2}}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\textstyle a}$ ${\textstyle b}$ $X_{3}={\frac {aX_{1}+bX_{2}-(a+b)\mu }{\sqrt {a^{2}+b^{2}}}}+\mu$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\textstyle \alpha =2}$
Si , son distribuciones normales, entonces su media geométrica normalizada es una distribución normal con y (ver aquí para una visualización). ${\textstyle X_{k}\sim {\mathcal {N}}(m_{k},\sigma _{k}^{2})}$ ${\textstyle k\in \{0,1\}}$ ${\textstyle {\frac {1}{\int _{\mathbb {R} ^{n}}X_{0}^{\alpha }(x)X_{1}^{1-\alpha }(x)\,{\text{d}}x}}X_{0}^{\alpha }X_{1}^{1-\alpha }}$ ${\textstyle {\mathcal {N}}(m_{\alpha },\sigma _{\alpha }^{2})}$ ${\textstyle m_{\alpha }={\frac {\alpha m_{0}\sigma _{1}^{2}+(1-\alpha )m_{1}\sigma _{0}^{2}}{\alpha \sigma _{1}^{2}+(1-\alpha )\sigma _{0}^{2}}}}$ ${\textstyle \sigma _{\alpha }^{2}={\frac {\sigma _{0}^{2}\sigma _{1}^{2}}{\alpha \sigma _{1}^{2}+(1-\alpha )\sigma _{0}^{2}}}}$

Operaciones sobre dos variables normales estándar independientes

Si y son dos variables aleatorias normales estándar independientes con media 0 y varianza 1, entonces ${\textstyle X_{1}}$ ${\textstyle X_{2}}$

Su suma y diferencia se distribuyen normalmente con media cero y varianza dos: . ${\textstyle X_{1}\pm X_{2}\sim {\mathcal {N}}(0,2)}$
Su producto sigue la distribución de producto ^[41] con función de densidad donde es la función de Bessel modificada de segundo tipo . Esta distribución es simétrica alrededor de cero, ilimitada en , y tiene la función característica . ${\textstyle Z=X_{1}X_{2}}$ ${\textstyle f_{Z}(z)=\pi ^{-1}K_{0}(|z|)}$ ${\textstyle K_{0}}$ ${\textstyle z=0}$ ${\textstyle \phi _{Z}(t)=(1+t^{2})^{-1/2}}$
Su relación sigue la distribución estándar de Cauchy : . ${\textstyle X_{1}/X_{2}\sim \operatorname {Cauchy} (0,1)}$
Su norma euclidiana tiene la distribución de Rayleigh . ${\textstyle {\sqrt {X_{1}^{2}+X_{2}^{2}}}}$

Operaciones sobre múltiples variables normales independientes

Cualquier combinación lineal de desviaciones normales independientes es una desviación normal.
Si son variables aleatorias normales estándar independientes, entonces la suma de sus cuadrados tiene la distribución de chi-cuadrado con grados de libertad. ${\textstyle X_{1},X_{2},\ldots ,X_{n}}$ ${\textstyle n}$ $X_{1}^{2}+\cdots +X_{n}^{2}\sim \chi _{n}^{2}.$
Si son variables aleatorias independientes distribuidas normalmente con medias y varianzas , entonces su media muestral es independiente de la desviación estándar muestral , ^[42] lo que se puede demostrar utilizando el teorema de Basu o el teorema de Cochran . ^[43] La relación de estas dos cantidades tendrá la distribución t de Student con grados de libertad: ${\textstyle X_{1},X_{2},\ldots ,X_{n}}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\textstyle n-1}$ $t={\frac {{\overline {X}}-\mu }{S/{\sqrt {n}}}}={\frac {{\frac {1}{n}}(X_{1}+\cdots +X_{n})-\mu }{\sqrt {{\frac {1}{n(n-1)}}\left[(X_{1}-{\overline {X}})^{2}+\cdots +(X_{n}-{\overline {X}})^{2}\right]}}}\sim t_{n-1}.$
Si , son variables aleatorias normales estándar independientes, entonces la relación de sus sumas de cuadrados normalizadas tendrá la distribución F con $($ $n$ $,$ $m$ $)$ grados de libertad: ^[44] ${\textstyle X_{1},X_{2},\ldots ,X_{n}}$ ${\textstyle Y_{1},Y_{2},\ldots ,Y_{m}}$ $F={\frac {\left(X_{1}^{2}+X_{2}^{2}+\cdots +X_{n}^{2}\right)/n}{\left(Y_{1}^{2}+Y_{2}^{2}+\cdots +Y_{m}^{2}\right)/m}}\sim F_{n,m}.$

Operaciones sobre múltiples variables normales correlacionadas

Una forma cuadrática de un vector normal, es decir, una función cuadrática de múltiples variables normales independientes o correlacionadas, es una variable de chi-cuadrado generalizada . ${\textstyle q=\sum x_{i}^{2}+\sum x_{j}+c}$

Operaciones sobre la función de densidad

La distribución normal dividida se define de manera más directa en términos de unir secciones escaladas de las funciones de densidad de diferentes distribuciones normales y reescalar la densidad para integrarla en una sola. La distribución normal truncada resulta de reescalar una sección de una sola función de densidad.

Divisibilidad infinita y teorema de Cramér

Para cualquier entero positivo , cualquier distribución normal con media y varianza es la distribución de la suma de desviaciones normales independientes, cada una con media y varianza . Esta propiedad se llama divisibilidad infinita . ^[45] ${\textstyle {\text{n}}}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\textstyle {\text{n}}}$ ${\textstyle {\frac {\mu }{n}}}$ ${\textstyle {\frac {\sigma ^{2}}{n}}}$

Por el contrario, si y son variables aleatorias independientes y su suma tiene una distribución normal, entonces tanto como deben ser desviaciones normales. ^[46] ${\textstyle X_{1}}$ ${\textstyle X_{2}}$ ${\textstyle X_{1}+X_{2}}$ ${\textstyle X_{1}}$ ${\textstyle X_{2}}$

Este resultado se conoce como teorema de descomposición de Cramér y equivale a decir que la convolución de dos distribuciones es normal si y solo si ambas son normales. El teorema de Cramér implica que una combinación lineal de variables independientes no gaussianas nunca tendrá una distribución exactamente normal, aunque puede aproximarse a ella de forma arbitraria. ^[31]

El teorema de Kac-Bernstein

El teorema de Kac-Bernstein establece que si y son independientes y y también son independientes, entonces tanto X como Y deben tener necesariamente distribuciones normales. ^[47]^[48] ${\textstyle X}$ ${\textstyle Y}$ ${\textstyle X+Y}$ ${\textstyle X-Y}$

De manera más general, si son variables aleatorias independientes, entonces dos combinaciones lineales distintas y serán independientes si y solo si todas son normales y , donde denota la varianza de . ^[47] ${\textstyle X_{1},\ldots ,X_{n}}$ ${\textstyle \sum {a_{k}X_{k}}}$ ${\textstyle \sum {b_{k}X_{k}}}$ ${\textstyle X_{k}}$ ${\textstyle \sum {a_{k}b_{k}\sigma _{k}^{2}=0}}$ ${\textstyle \sigma _{k}^{2}}$ ${\textstyle X_{k}}$

Extensiones

El concepto de distribución normal, una de las distribuciones más importantes en la teoría de la probabilidad, se ha extendido mucho más allá del marco estándar del caso univariado (es decir, unidimensional) (caso 1). Todas estas extensiones también se denominan leyes normales o gaussianas , por lo que existe cierta ambigüedad en sus nombres.

La distribución normal multivariante describe la ley de Gauss en el espacio euclidiano de dimensión k . Un vector X ∈ R ^k tiene una distribución normal multivariante si cualquier combinación lineal de sus componentes Σ^kj₌
₁a _j X _j tiene una distribución normal (univariada). La varianza de X es unamatriz positiva definida simétrica k×k V . La distribución normal multivariada es un caso especial de las distribuciones elípticas . Como tal, sus lugares de isodensidad en el caso k = 2 son elipses y en el caso de k arbitrario son elipsoides .
Distribución gaussiana rectificada: una versión rectificada de la distribución normal con todos los elementos negativos restablecidos a 0.
La distribución normal compleja se ocupa de los vectores normales complejos. Se dice que un vector complejo X ∈ C ^k es normal si sus componentes reales e imaginarios poseen conjuntamente una distribución normal multivariante de 2 k dimensiones. La estructura de varianza-covarianza de X se describe mediante dos matrices: la matriz de varianza Γ y la matriz de relación C .
La distribución normal matricial describe el caso de matrices distribuidas normalmente.
Los procesos gaussianos son procesos estocásticos distribuidos normalmente . Estos pueden verse como elementos de algún espacio de Hilbert de dimensión infinita H y, por lo tanto, son los análogos de los vectores normales multivariados para el caso k = ∞ . Se dice que un elemento aleatorio h ∈ H es normal si para cualquier constante a ∈ H el producto escalar ( a , h ) tiene una distribución normal (univariada). La estructura de varianza de dicho elemento aleatorio gaussiano puede describirse en términos del operador de covarianza lineal K: H → H . Varios procesos gaussianos se hicieron lo suficientemente populares como para tener sus propios nombres:
- movimiento browniano
- Puente browniano ,
- Proceso de Ornstein-Uhlenbeck .
La distribución q gaussiana es una construcción matemática abstracta que representa un análogo q de la distribución normal.
La distribución q-gaussiana es análoga a la distribución gaussiana, en el sentido de que maximiza la entropía de Tsallis y es un tipo de distribución de Tsallis . Esta distribución es diferente de la distribución q gaussiana anterior.
La distribución κ -Gaussiana de Kaniadakis es una generalización de la distribución Gaussiana que surge de las estadísticas de Kaniadakis , siendo una de las distribuciones de Kaniadakis .

Una variable aleatoria X tiene una distribución normal de dos piezas si tiene una distribución

$f_{X}(x)=N(\mu ,\sigma _{1}^{2}){\text{ if }}x\leq \mu$ $f_{X}(x)=N(\mu ,\sigma _{2}^{2}){\text{ if }}x\geq \mu$

donde μ es la media y σ ₁² y σ ₂² son las varianzas de la distribución a la izquierda y a la derecha de la media respectivamente.

Se han determinado la media, la varianza y el tercer momento central de esta distribución ^[49]

$\operatorname {E} (X)=\mu +{\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})$ $\operatorname {V} (X)=\left(1-{\frac {2}{\pi }}\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}$ $\operatorname {T} (X)={\sqrt {\frac {2}{\pi }}}(\sigma _{2}-\sigma _{1})\left[\left({\frac {4}{\pi }}-1\right)(\sigma _{2}-\sigma _{1})^{2}+\sigma _{1}\sigma _{2}\right]$

donde E( X ), V( X ) y T( X ) son la media, la varianza y el tercer momento central respectivamente.

Uno de los principales usos prácticos de la ley de Gauss es modelar las distribuciones empíricas de muchas variables aleatorias diferentes que se encuentran en la práctica. En tal caso, una posible extensión sería una familia más rica de distribuciones, que tuviera más de dos parámetros y, por lo tanto, pudiera ajustarse a la distribución empírica con mayor precisión. Los ejemplos de tales extensiones son:

Distribución de Pearson : una familia de distribuciones de probabilidad de cuatro parámetros que extienden la ley normal para incluir diferentes valores de asimetría y curtosis.
La distribución normal generalizada , también conocida como distribución de potencia exponencial, permite colas de distribución con comportamientos asintóticos más gruesos o más delgados.

Inferencia estadística

Estimación de parámetros

A menudo sucede que no conocemos los parámetros de la distribución normal, pero queremos estimarlos . Es decir, si tenemos una muestra de una población normal, nos gustaría conocer los valores aproximados de los parámetros y . El enfoque estándar para este problema es el método de máxima verosimilitud , que requiere maximizar la función de log-verosimilitud : ${\textstyle (x_{1},\ldots ,x_{n})}$ ${\textstyle {\mathcal {N}}(\mu ,\sigma ^{2})}$ ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ $\ln {\mathcal {L}}(\mu ,\sigma ^{2})=\sum _{i=1}^{n}\ln f(x_{i}\mid \mu ,\sigma ^{2})=-{\frac {n}{2}}\ln(2\pi )-{\frac {n}{2}}\ln \sigma ^{2}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}.$ Tomando derivadas con respecto a y y resolviendo el sistema resultante de condiciones de primer orden se obtienen las estimaciones de máxima verosimilitud : ${\textstyle \mu }$ ${\textstyle \sigma ^{2}}$ ${\hat {\mu }}={\overline {x}}\equiv {\frac {1}{n}}\sum _{i=1}^{n}x_{i},\qquad {\hat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}.$

Entonces es como sigue: ${\textstyle \ln {\mathcal {L}}({\hat {\mu }},{\hat {\sigma }}^{2})}$

$\ln {\mathcal {L}}({\hat {\mu }},{\hat {\sigma }}^{2})=(-n/2)[\ln(2\pi {\hat {\sigma }}^{2})+1]$

Media de la muestra

El estimador se denomina media muestral , ya que es la media aritmética de todas las observaciones. La estadística es completa y suficiente para , y por lo tanto, por el teorema de Lehmann-Scheffé , es el estimador insesgado de varianza mínima uniforme (UMVU). ^[50] En muestras finitas se distribuye normalmente: La varianza de este estimador es igual al elemento μμ de la matriz de información de Fisher inversa . Esto implica que el estimador es eficiente en muestras finitas . De importancia práctica es el hecho de que el error estándar de es proporcional a , es decir, si uno desea disminuir el error estándar en un factor de 10, uno debe aumentar el número de puntos en la muestra en un factor de 100. Este hecho se usa ampliamente para determinar los tamaños de muestra para las encuestas de opinión y el número de ensayos en las simulaciones de Monte Carlo . $\textstyle {\hat {\mu }}$ $\textstyle {\overline {x}}$ ${\textstyle \mu }$ $\textstyle {\hat {\mu }}$ ${\hat {\mu }}\sim {\mathcal {N}}(\mu ,\sigma ^{2}/n).$ $\textstyle {\mathcal {I}}^{-1}$ $\textstyle {\hat {\mu }}$ $\textstyle 1/{\sqrt {n}}$

Desde el punto de vista de la teoría asintótica , es consistente , es decir, converge en probabilidad a cuando . El estimador también es asintóticamente normal , lo que es un corolario simple del hecho de que es normal en muestras finitas: $\textstyle {\hat {\mu }}$ ${\textstyle \mu }$ ${\textstyle n\rightarrow \infty }$ ${\sqrt {n}}({\hat {\mu }}-\mu )\,\xrightarrow {d} \,{\mathcal {N}}(0,\sigma ^{2}).$

Varianza de la muestra

El estimador se denomina varianza muestral , ya que es la varianza de la muestra ( ). En la práctica, a menudo se utiliza otro estimador en lugar del . Este otro estimador se denota , y también se denomina varianza muestral , lo que representa una cierta ambigüedad en la terminología; su raíz cuadrada se denomina desviación estándar muestral . El estimador se diferencia de por tener ( n − 1) en lugar de n en el denominador (la llamada corrección de Bessel ): La diferencia entre y se vuelve insignificantemente pequeña para n grandes . Sin embargo, en muestras finitas, la motivación detrás del uso de es que es un estimador insesgado del parámetro subyacente , mientras que está sesgado. Además, por el teorema de Lehmann-Scheffé, el estimador es uniformemente de varianza mínima insesgado ( UMVU ), ^[50] lo que lo convierte en el "mejor" estimador entre todos los insesgados. Sin embargo, se puede demostrar que el estimador sesgado es mejor que el en términos del criterio de error cuadrático medio (MSE). En muestras finitas, tanto y tienen una distribución chi-cuadrado escalada con ( n − 1) grados de libertad: La primera de estas expresiones muestra que la varianza de es igual a , que es ligeramente mayor que el elemento σσ de la matriz de información de Fisher inversa . Por lo tanto, no es un estimador eficiente para , y además, dado que es UMVU, podemos concluir que el estimador eficiente de muestra finita para no existe. $\textstyle {\hat {\sigma }}^{2}$ ${\textstyle (x_{1},\ldots ,x_{n})}$ $\textstyle {\hat {\sigma }}^{2}$ ${\textstyle s^{2}}$ ${\textstyle s}$ ${\textstyle s^{2}}$ $\textstyle {\hat {\sigma }}^{2}$ $s^{2}={\frac {n}{n-1}}{\hat {\sigma }}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}.$ ${\textstyle s^{2}}$ $\textstyle {\hat {\sigma }}^{2}$ ${\textstyle s^{2}}$ ${\textstyle \sigma ^{2}}$ $\textstyle {\hat {\sigma }}^{2}$ ${\textstyle s^{2}}$ $\textstyle {\hat {\sigma }}^{2}$ ${\textstyle s^{2}}$ ${\textstyle s^{2}}$ $\textstyle {\hat {\sigma }}^{2}$ $s^{2}\sim {\frac {\sigma ^{2}}{n-1}}\cdot \chi _{n-1}^{2},\qquad {\hat {\sigma }}^{2}\sim {\frac {\sigma ^{2}}{n}}\cdot \chi _{n-1}^{2}.$ ${\textstyle s^{2}}$ ${\textstyle 2\sigma ^{4}/(n-1)}$ $\textstyle {\mathcal {I}}^{-1}$ ${\textstyle s^{2}}$ ${\textstyle \sigma ^{2}}$ ${\textstyle s^{2}}$ ${\textstyle \sigma ^{2}}$

Aplicando la teoría asintótica, ambos estimadores y son consistentes, es decir, convergen en probabilidad a cuando el tamaño de la muestra es . Los dos estimadores también son asintóticamente normales: En particular, ambos estimadores son asintóticamente eficientes para . ${\textstyle s^{2}}$ $\textstyle {\hat {\sigma }}^{2}$ ${\textstyle \sigma ^{2}}$ ${\textstyle n\rightarrow \infty }$ ${\sqrt {n}}({\hat {\sigma }}^{2}-\sigma ^{2})\simeq {\sqrt {n}}(s^{2}-\sigma ^{2})\,\xrightarrow {d} \,{\mathcal {N}}(0,2\sigma ^{4}).$ ${\textstyle \sigma ^{2}}$

Intervalos de confianza

Por el teorema de Cochran , para distribuciones normales la media muestral y la varianza muestral s ² son independientes , lo que significa que no puede haber ganancia en considerar su distribución conjunta . También hay un teorema inverso: si en una muestra la media muestral y la varianza muestral son independientes, entonces la muestra debe provenir de la distribución normal. La independencia entre y s se puede emplear para construir el llamado estadístico t : Esta cantidad t tiene la distribución t de Student con ( n − 1) grados de libertad, y es un estadístico auxiliar (independiente del valor de los parámetros). Invertir la distribución de este estadístico t nos permitirá construir el intervalo de confianza para μ ; ^[51] de manera similar, invertir la distribución χ ² del estadístico s ² nos dará el intervalo de confianza para σ ² : ^[52] donde t _k,p y χ $\textstyle {\hat {\mu }}$ $\textstyle {\hat {\mu }}$ $t={\frac {{\hat {\mu }}-\mu }{s/{\sqrt {n}}}}={\frac {{\overline {x}}-\mu }{\sqrt {{\frac {1}{n(n-1)}}\sum (x_{i}-{\overline {x}})^{2}}}}\sim t_{n-1}$ $\mu \in \left[{\hat {\mu }}-{\frac {t_{n-1,1-\alpha /2}}{\sqrt {n}}}s,\,{\hat {\mu }}+{\frac {t_{n-1,1-\alpha /2}}{\sqrt {n}}}s\right],$ $\sigma ^{2}\in \left[{\frac {n-1}{\chi _{n-1,1-\alpha /2}^{2}}}s^{2},\,{\frac {n-1}{\chi _{n-1,\alpha /2}^{2}}}s^{2}\right],$ 2
k,p son los cuantiles p de las distribuciones t y χ ^{2 ,} respectivamente. Estos intervalos de confianza tienen un nivel de confianza de 1 − α , lo que significa que los valores verdaderos μ y σ ² quedan fuera de estos intervalos con una probabilidad (o nivel de significancia ) α . En la práctica, la gente suele tomar α = 5% , lo que da como resultado intervalos de confianza del 95%. El intervalo de confianza para σ se puede encontrar tomando la raíz cuadrada de los límites del intervalo para σ ² .

Se pueden derivar fórmulas aproximadas a partir de las distribuciones asintóticas de y s ² : Las fórmulas aproximadas se vuelven válidas para valores grandes de n , y son más convenientes para el cálculo manual ya que los cuantiles normales estándar z _α_/2 no dependen de n . En particular, el valor más popular de α = 5% , da como resultado | z _0,025 | = 1,96 . $\textstyle {\hat {\mu }}$ $\mu \in \left[{\hat {\mu }}-{\frac {|z_{\alpha /2}|}{\sqrt {n}}}s,\,{\hat {\mu }}+{\frac {|z_{\alpha /2}|}{\sqrt {n}}}s\right],$ $\sigma ^{2}\in \left[s^{2}-{\sqrt {2}}{\frac {|z_{\alpha /2}|}{\sqrt {n}}}s^{2},\,s^{2}+{\sqrt {2}}{\frac {|z_{\alpha /2}|}{\sqrt {n}}}s^{2}\right],$

Pruebas de normalidad

Las pruebas de normalidad evalúan la probabilidad de que el conjunto de datos dado { x ₁ , ..., x _n } provenga de una distribución normal. Normalmente, la hipótesis nula H ₀ es que las observaciones se distribuyen normalmente con una media μ y una varianza σ ² no especificadas , frente a la alternativa H _a de que la distribución es arbitraria. Se han ideado muchas pruebas (más de 40) para este problema. Las más destacadas se describen a continuación:

Los gráficos de diagnóstico son más atractivos intuitivamente, pero subjetivos al mismo tiempo, ya que se basan en el juicio humano informal para aceptar o rechazar la hipótesis nula.

El gráfico Q–Q , también conocido como gráfico de probabilidad normal o gráfico de Rankit , es un gráfico de los valores ordenados del conjunto de datos contra los valores esperados de los cuantiles correspondientes de la distribución normal estándar. Es decir, es un gráfico de puntos de la forma (Φ ⁻¹ ( p _k ), x _{( k )} ), donde los puntos de trazado p _k son iguales a p _k = ( k − α )/( n + 1 − 2 α ) y α es una constante de ajuste, que puede ser cualquier valor entre 0 y 1. Si la hipótesis nula es verdadera, los puntos trazados deben estar aproximadamente en una línea recta.
Diagrama P–P : similar al diagrama Q–Q, pero usado con mucha menos frecuencia. Este método consiste en representar gráficamente los puntos (Φ( z _{( k )} ), p _k ), donde . Para datos distribuidos normalmente, este diagrama debe estar en una línea de 45° entre (0, 0) y (1, 1). ${\textstyle \textstyle z_{(k)}=(x_{(k)}-{\hat {\mu }})/{\hat {\sigma }}}$

Pruebas de bondad de ajuste :

Pruebas basadas en momentos :

Prueba del K-cuadrado de D'Agostino
Prueba de Jarque-Bera
Prueba de Shapiro-Wilk : se basa en el hecho de que la línea en el gráfico Q-Q tiene una pendiente de σ . La prueba compara la estimación de mínimos cuadrados de esa pendiente con el valor de la varianza de la muestra y rechaza la hipótesis nula si estas dos cantidades difieren significativamente.

Pruebas basadas en la función de distribución empírica :

Prueba de Anderson-Darling
Prueba de Lilliefors (una adaptación de la prueba de Kolmogorov-Smirnov )

Análisis bayesiano de la distribución normal

El análisis bayesiano de datos distribuidos normalmente se complica por las muchas posibilidades diferentes que pueden considerarse:

Tanto la media como la varianza, o ninguna de ellas, pueden considerarse una cantidad fija.
Cuando se desconoce la varianza, el análisis puede realizarse directamente en términos de la varianza o en términos de la precisión , el recíproco de la varianza. La razón para expresar las fórmulas en términos de precisión es que se simplifica el análisis de la mayoría de los casos.
Es necesario considerar tanto los casos univariados como los multivariados .
Se pueden colocar distribuciones previas conjugadas o impropias en las variables desconocidas.
En la regresión lineal bayesiana se da un conjunto adicional de casos , en los que en el modelo básico se supone que los datos se distribuyen normalmente y se aplican valores a priori normales a los coeficientes de regresión . El análisis resultante es similar a los casos básicos de datos independientes distribuidos de forma idéntica .

Las fórmulas para los casos de regresión no lineal se resumen en el artículo anterior conjugado .

Suma de dos cuadráticas

Forma escalar

La siguiente fórmula auxiliar es útil para simplificar las ecuaciones de actualización posterior , que de otro modo se vuelven bastante tediosas.

$a(x-y)^{2}+b(x-z)^{2}=(a+b)\left(x-{\frac {ay+bz}{a+b}}\right)^{2}+{\frac {ab}{a+b}}(y-z)^{2}$

Esta ecuación reescribe la suma de dos ecuaciones cuadráticas en x expandiendo los cuadrados, agrupando los términos en x y completando el cuadrado . Tenga en cuenta lo siguiente sobre los factores constantes complejos asociados a algunos de los términos:

El factor tiene la forma de un promedio ponderado de y y z . ${\textstyle {\frac {ay+bz}{a+b}}}$
${\textstyle {\frac {ab}{a+b}}={\frac {1}{{\frac {1}{a}}+{\frac {1}{b}}}}=(a^{-1}+b^{-1})^{-1}.}$ Esto demuestra que este factor puede considerarse como el resultado de una situación en la que los recíprocos de las cantidades a y b se suman directamente, de modo que para combinar a y b , es necesario recíprocar, sumar y recíprocar el resultado nuevamente para volver a las unidades originales. Este es exactamente el tipo de operación que realiza la media armónica , por lo que no es sorprendente que sea la mitad de la media armónica de a y b . ${\textstyle {\frac {ab}{a+b}}}$

Forma vectorial

Se puede escribir una fórmula similar para la suma de dos cuadráticas vectoriales: Si x , y , z son vectores de longitud k , y A y B son matrices simétricas e invertibles de tamaño , entonces ${\textstyle k\times k}$

${\begin{aligned}&(\mathbf {y} -\mathbf {x} )'\mathbf {A} (\mathbf {y} -\mathbf {x} )+(\mathbf {x} -\mathbf {z} )'\mathbf {B} (\mathbf {x} -\mathbf {z} )\\={}&(\mathbf {x} -\mathbf {c} )'(\mathbf {A} +\mathbf {B} )(\mathbf {x} -\mathbf {c} )+(\mathbf {y} -\mathbf {z} )'(\mathbf {A} ^{-1}+\mathbf {B} ^{-1})^{-1}(\mathbf {y} -\mathbf {z} )\end{aligned}}$

dónde

$\mathbf {c} =(\mathbf {A} +\mathbf {B} )^{-1}(\mathbf {A} \mathbf {y} +\mathbf {B} \mathbf {z} )$

La forma x ′ A x se llama forma cuadrática y es un escalar : En otras palabras, suma todas las combinaciones posibles de productos de pares de elementos de x , con un coeficiente separado para cada uno. Además, como , solo importa la suma para cualquier elemento fuera de la diagonal de A , y no hay pérdida de generalidad al suponer que A es simétrico . Además, si A es simétrico, entonces la forma $\mathbf {x} '\mathbf {A} \mathbf {x} =\sum _{i,j}a_{ij}x_{i}x_{j}$ ${\textstyle x_{i}x_{j}=x_{j}x_{i}}$ ${\textstyle a_{ij}+a_{ji}}$ ${\textstyle \mathbf {x} '\mathbf {A} \mathbf {y} =\mathbf {y} '\mathbf {A} \mathbf {x} .}$

Suma de las diferencias con respecto a la media

Otra fórmula útil es la siguiente: donde $\sum _{i=1}^{n}(x_{i}-\mu )^{2}=\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}$ ${\textstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}.}$

Con varianza conocida

Para un conjunto de puntos de datos iid distribuidos normalmente X de tamaño n , donde cada punto individual x sigue con una varianza conocida σ ² , la distribución previa conjugada también se distribuye normalmente. ${\textstyle x\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$

Esto se puede demostrar más fácilmente reescribiendo la varianza como la precisión , es decir, utilizando τ = 1/σ ² . Entonces, si y procedemos de la siguiente manera. ${\textstyle x\sim {\mathcal {N}}(\mu ,1/\tau )}$ ${\textstyle \mu \sim {\mathcal {N}}(\mu _{0},1/\tau _{0}),}$

En primer lugar, la función de verosimilitud es (utilizando la fórmula anterior para la suma de las diferencias con respecto a la media):

${\begin{aligned}p(\mathbf {X} \mid \mu ,\tau )&=\prod _{i=1}^{n}{\sqrt {\frac {\tau }{2\pi }}}\exp \left(-{\frac {1}{2}}\tau (x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left(-{\frac {1}{2}}\tau \sum _{i=1}^{n}(x_{i}-\mu )^{2}\right)\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right].\end{aligned}}$

Luego procedemos de la siguiente manera:

${\begin{aligned}p(\mu \mid \mathbf {X} )&\propto p(\mathbf {X} \mid \mu )p(\mu )\\&=\left({\frac {\tau }{2\pi }}\right)^{n/2}\exp \left[-{\frac {1}{2}}\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]{\sqrt {\frac {\tau _{0}}{2\pi }}}\exp \left(-{\frac {1}{2}}\tau _{0}(\mu -\mu _{0})^{2}\right)\\&\propto \exp \left(-{\frac {1}{2}}\left(\tau \left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)+\tau _{0}(\mu -\mu _{0})^{2}\right)\right)\\&\propto \exp \left(-{\frac {1}{2}}\left(n\tau ({\bar {x}}-\mu )^{2}+\tau _{0}(\mu -\mu _{0})^{2}\right)\right)\\&=\exp \left(-{\frac {1}{2}}(n\tau +\tau _{0})\left(\mu -{\dfrac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\right)^{2}+{\frac {n\tau \tau _{0}}{n\tau +\tau _{0}}}({\bar {x}}-\mu _{0})^{2}\right)\\&\propto \exp \left(-{\frac {1}{2}}(n\tau +\tau _{0})\left(\mu -{\dfrac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\right)^{2}\right)\end{aligned}}$

En la derivación anterior, utilizamos la fórmula anterior para la suma de dos cuadráticas y eliminamos todos los factores constantes que no involucran μ . El resultado es el núcleo de una distribución normal, con media y precisión , es decir ${\textstyle {\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}}$ ${\textstyle n\tau +\tau _{0}}$

$p(\mu \mid \mathbf {X} )\sim {\mathcal {N}}\left({\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}},{\frac {1}{n\tau +\tau _{0}}}\right)$

Esto se puede escribir como un conjunto de ecuaciones de actualización bayesianas para los parámetros posteriores en términos de los parámetros anteriores:

${\begin{aligned}\tau _{0}'&=\tau _{0}+n\tau \\[5pt]\mu _{0}'&={\frac {n\tau {\bar {x}}+\tau _{0}\mu _{0}}{n\tau +\tau _{0}}}\\[5pt]{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\end{aligned}}$

Es decir, combinar n puntos de datos con precisión total de nτ (o equivalentemente, varianza total de n / σ ² ) y media de valores , derivar una nueva precisión total simplemente sumando la precisión total de los datos a la precisión total previa, y formar una nueva media a través de un promedio ponderado por precisión , es decir, un promedio ponderado de la media de los datos y la media previa, cada una ponderada por la precisión total asociada. Esto tiene sentido lógico si se piensa que la precisión indica la certeza de las observaciones: en la distribución de la media posterior, cada uno de los componentes de entrada está ponderado por su certeza, y la certeza de esta distribución es la suma de las certezas individuales. (Para la intuición de esto, compare la expresión "el todo es (o no es) mayor que la suma de sus partes". Además, considere que el conocimiento de la posterior proviene de una combinación del conocimiento de la anterior y la probabilidad, por lo que tiene sentido que estemos más seguros de él que de cualquiera de sus componentes). ${\textstyle {\bar {x}}}$

La fórmula anterior revela por qué es más conveniente realizar un análisis bayesiano de valores anteriores conjugados para la distribución normal en términos de precisión. La precisión posterior es simplemente la suma de las precisiones previa y de verosimilitud, y la media posterior se calcula a través de un promedio ponderado por precisión, como se describió anteriormente. Las mismas fórmulas se pueden escribir en términos de varianza al reciprocar todas las precisiones, lo que produce las fórmulas más feas.

${\begin{aligned}{\sigma _{0}^{2}}'&={\frac {1}{{\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}}}\\[5pt]\mu _{0}'&={\frac {{\frac {n{\bar {x}}}{\sigma ^{2}}}+{\frac {\mu _{0}}{\sigma _{0}^{2}}}}{{\frac {n}{\sigma ^{2}}}+{\frac {1}{\sigma _{0}^{2}}}}}\\[5pt]{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\end{aligned}}$

Con media conocida

Para un conjunto de puntos de datos distribuidos normalmente iid X de tamaño n donde cada punto individual x sigue con media conocida μ, la distribución previa conjugada de la varianza tiene una distribución gamma inversa o una distribución chi-cuadrado inversa escalada . Las dos son equivalentes excepto por tener diferentes parametrizaciones . Aunque la gamma inversa se usa más comúnmente, usamos la chi-cuadrado inversa escalada por conveniencia. La distribución previa para σ ² es la siguiente: ${\textstyle x\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$

$p(\sigma ^{2}\mid \nu _{0},\sigma _{0}^{2})={\frac {(\sigma _{0}^{2}{\frac {\nu _{0}}{2}})^{\nu _{0}/2}}{\Gamma \left({\frac {\nu _{0}}{2}}\right)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\propto {\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}$

La función de probabilidad de arriba, escrita en términos de la varianza, es:

${\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}\right]\\&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {S}{2\sigma ^{2}}}\right]\end{aligned}}$

dónde

$S=\sum _{i=1}^{n}(x_{i}-\mu )^{2}.$

Entonces:

${\begin{aligned}p(\sigma ^{2}\mid \mathbf {X} )&\propto p(\mathbf {X} \mid \sigma ^{2})p(\sigma ^{2})\\&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {S}{2\sigma ^{2}}}\right]{\frac {(\sigma _{0}^{2}{\frac {\nu _{0}}{2}})^{\frac {\nu _{0}}{2}}}{\Gamma \left({\frac {\nu _{0}}{2}}\right)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\\&\propto \left({\frac {1}{\sigma ^{2}}}\right)^{n/2}{\frac {1}{(\sigma ^{2})^{1+{\frac {\nu _{0}}{2}}}}}\exp \left[-{\frac {S}{2\sigma ^{2}}}+{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]\\&={\frac {1}{(\sigma ^{2})^{1+{\frac {\nu _{0}+n}{2}}}}}\exp \left[-{\frac {\nu _{0}\sigma _{0}^{2}+S}{2\sigma ^{2}}}\right]\end{aligned}}$

Lo anterior también es una distribución chi-cuadrado inversa escalada donde

${\begin{aligned}\nu _{0}'&=\nu _{0}+n\\\nu _{0}'{\sigma _{0}^{2}}'&=\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-\mu )^{2}\end{aligned}}$

o equivalentemente

${\begin{aligned}\nu _{0}'&=\nu _{0}+n\\{\sigma _{0}^{2}}'&={\frac {\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-\mu )^{2}}{\nu _{0}+n}}\end{aligned}}$

Reparametrizando en términos de una distribución gamma inversa , el resultado es:

${\begin{aligned}\alpha '&=\alpha +{\frac {n}{2}}\\\beta '&=\beta +{\frac {\sum _{i=1}^{n}(x_{i}-\mu )^{2}}{2}}\end{aligned}}$

Con media desconocida y varianza desconocida

Para un conjunto de puntos de datos distribuidos normalmente iid X de tamaño n donde cada punto individual x sigue con media desconocida μ y varianza desconocida σ ^{2 , se coloca una}distribución previa conjugada combinada (multivariada) sobre la media y la varianza, que consiste en una distribución gamma inversa normal . Lógicamente, esto se origina de la siguiente manera: ${\textstyle x\sim {\mathcal {N}}(\mu ,\sigma ^{2})}$

A partir del análisis del caso con media desconocida pero varianza conocida, vemos que las ecuaciones de actualización involucran estadísticas suficientes calculadas a partir de los datos que consisten en la media de los puntos de datos y la varianza total de los puntos de datos, calculada a su vez a partir de la varianza conocida dividida por el número de puntos de datos.
A partir del análisis del caso con varianza desconocida pero media conocida, vemos que las ecuaciones de actualización involucran estadísticas suficientes sobre los datos que consisten en el número de puntos de datos y la suma de las desviaciones al cuadrado .
Tenga en cuenta que los valores de actualización posteriores sirven como distribución a priori cuando se manejan más datos. Por lo tanto, lógicamente deberíamos pensar en nuestros valores a priori en términos de las estadísticas suficientes que acabamos de describir, teniendo en cuenta la misma semántica tanto como sea posible.
Para manejar el caso en el que tanto la media como la varianza son desconocidas, podríamos colocar valores a priori independientes sobre la media y la varianza, con estimaciones fijas de la media promedio, la varianza total, el número de puntos de datos utilizados para calcular el valor a priori de la varianza y la suma de las desviaciones al cuadrado. Sin embargo, tenga en cuenta que, en realidad, la varianza total de la media depende de la varianza desconocida, y la suma de las desviaciones al cuadrado que entran en el valor a priori de la varianza (parece) depende de la media desconocida. En la práctica, esta última dependencia es relativamente poco importante: al cambiar la media real, se cambian los puntos generados en una cantidad igual y, en promedio, las desviaciones al cuadrado permanecerán iguales. Sin embargo, este no es el caso con la varianza total de la media: a medida que aumenta la varianza desconocida, la varianza total de la media aumentará proporcionalmente y nos gustaría capturar esta dependencia.
Esto sugiere que creamos una previa condicional de la media sobre la varianza desconocida, con un hiperparámetro que especifica la media de las pseudoobservaciones asociadas con la previa, y otro parámetro que especifica el número de pseudoobservaciones. Este número sirve como un parámetro de escala sobre la varianza, lo que hace posible controlar la varianza general de la media en relación con el parámetro de varianza real. La previa para la varianza también tiene dos hiperparámetros, uno que especifica la suma de las desviaciones al cuadrado de las pseudoobservaciones asociadas con la previa, y otro que especifica una vez más el número de pseudoobservaciones. Cada una de las previas tiene un hiperparámetro que especifica el número de pseudoobservaciones, y en cada caso esto controla la varianza relativa de esa previa. Estos se dan como dos hiperparámetros separados para que la varianza (también conocida como la confianza) de las dos previas se pueda controlar por separado.
Esto conduce inmediatamente a la distribución normal-inversa-gamma , que es el producto de las dos distribuciones recién definidas, con valores anteriores conjugados utilizados (una distribución gamma inversa sobre la varianza y una distribución normal sobre la media, condicional a la varianza) y con los mismos cuatro parámetros recién definidos.

Los valores anteriores normalmente se definen de la siguiente manera:

${\begin{aligned}p(\mu \mid \sigma ^{2};\mu _{0},n_{0})&\sim {\mathcal {N}}(\mu _{0},\sigma ^{2}/n_{0})\\p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})&\sim I\chi ^{2}(\nu _{0},\sigma _{0}^{2})=IG(\nu _{0}/2,\nu _{0}\sigma _{0}^{2}/2)\end{aligned}}$

Las ecuaciones de actualización se pueden derivar y tienen el siguiente aspecto:

${\begin{aligned}{\bar {x}}&={\frac {1}{n}}\sum _{i=1}^{n}x_{i}\\\mu _{0}'&={\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\\n_{0}'&=n_{0}+n\\\nu _{0}'&=\nu _{0}+n\\\nu _{0}'{\sigma _{0}^{2}}'&=\nu _{0}\sigma _{0}^{2}+\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\end{aligned}}$

Los respectivos números de pseudoobservaciones suman el número de observaciones reales. El nuevo hiperparámetro medio es nuevamente un promedio ponderado, esta vez ponderado por los números relativos de observaciones. Finalmente, la actualización para es similar al caso con la media conocida, pero en este caso la suma de las desviaciones al cuadrado se toma con respecto a la media de los datos observados en lugar de la media verdadera y, como resultado, se debe agregar un nuevo término de interacción para ocuparse de la fuente de error adicional que surge de la desviación entre la media anterior y la de los datos. ${\textstyle \nu _{0}'{\sigma _{0}^{2}}'}$

Prueba

Las distribuciones anteriores son ${\begin{aligned}p(\mu \mid \sigma ^{2};\mu _{0},n_{0})&\sim {\mathcal {N}}(\mu _{0},\sigma ^{2}/n_{0})={\frac {1}{\sqrt {2\pi {\frac {\sigma ^{2}}{n_{0}}}}}}\exp \left(-{\frac {n_{0}}{2\sigma ^{2}}}(\mu -\mu _{0})^{2}\right)\\&\propto (\sigma ^{2})^{-1/2}\exp \left(-{\frac {n_{0}}{2\sigma ^{2}}}(\mu -\mu _{0})^{2}\right)\\p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})&\sim I\chi ^{2}(\nu _{0},\sigma _{0}^{2})=IG(\nu _{0}/2,\nu _{0}\sigma _{0}^{2}/2)\\&={\frac {(\sigma _{0}^{2}\nu _{0}/2)^{\nu _{0}/2}}{\Gamma (\nu _{0}/2)}}~{\frac {\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right]}{(\sigma ^{2})^{1+\nu _{0}/2}}}\\&\propto {(\sigma ^{2})^{-(1+\nu _{0}/2)}}\exp \left[{\frac {-\nu _{0}\sigma _{0}^{2}}{2\sigma ^{2}}}\right].\end{aligned}}$

Por lo tanto, el conjunto anterior es

${\begin{aligned}p(\mu ,\sigma ^{2};\mu _{0},n_{0},\nu _{0},\sigma _{0}^{2})&=p(\mu \mid \sigma ^{2};\mu _{0},n_{0})\,p(\sigma ^{2};\nu _{0},\sigma _{0}^{2})\\&\propto (\sigma ^{2})^{-(\nu _{0}+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+n_{0}(\mu -\mu _{0})^{2}\right)\right].\end{aligned}}$

La función de probabilidad de la sección anterior con varianza conocida es:

${\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\sum _{i=1}^{n}(x_{i}-\mu )^{2}\right)\right]\end{aligned}}$

Escribiéndolo en términos de varianza en lugar de precisión, obtenemos: donde ${\begin{aligned}p(\mathbf {X} \mid \mu ,\sigma ^{2})&=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]\\&\propto {\sigma ^{2}}^{-n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(S+n({\bar {x}}-\mu )^{2}\right)\right]\end{aligned}}$ ${\textstyle S=\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}.}$

Por lo tanto, la posterior es (eliminando los hiperparámetros como factores condicionantes): ${\begin{aligned}p(\mu ,\sigma ^{2}\mid \mathbf {X} )&\propto p(\mu ,\sigma ^{2})\,p(\mathbf {X} \mid \mu ,\sigma ^{2})\\&\propto (\sigma ^{2})^{-(\nu _{0}+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+n_{0}(\mu -\mu _{0})^{2}\right)\right]{\sigma ^{2}}^{-n/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(S+n({\bar {x}}-\mu )^{2}\right)\right]\\&=(\sigma ^{2})^{-(\nu _{0}+n+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+n_{0}(\mu -\mu _{0})^{2}+n({\bar {x}}-\mu )^{2}\right)\right]\\&=(\sigma ^{2})^{-(\nu _{0}+n+3)/2}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}+(n_{0}+n)\left(\mu -{\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\right)^{2}\right)\right]\\&\propto (\sigma ^{2})^{-1/2}\exp \left[-{\frac {n_{0}+n}{2\sigma ^{2}}}\left(\mu -{\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}}\right)^{2}\right]\\&\quad \times (\sigma ^{2})^{-(\nu _{0}/2+n/2+1)}\exp \left[-{\frac {1}{2\sigma ^{2}}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\right)\right]\\&={\mathcal {N}}_{\mu \mid \sigma ^{2}}\left({\frac {n_{0}\mu _{0}+n{\bar {x}}}{n_{0}+n}},{\frac {\sigma ^{2}}{n_{0}+n}}\right)\cdot {\rm {IG}}_{\sigma ^{2}}\left({\frac {1}{2}}(\nu _{0}+n),{\frac {1}{2}}\left(\nu _{0}\sigma _{0}^{2}+S+{\frac {n_{0}n}{n_{0}+n}}(\mu _{0}-{\bar {x}})^{2}\right)\right).\end{aligned}}$

En otras palabras, la distribución posterior tiene la forma de un producto de una distribución normal sobre , por una distribución gamma inversa sobre , con parámetros que son los mismos que las ecuaciones de actualización anteriores. ${\textstyle p(\mu |\sigma ^{2})}$ ${\textstyle p(\sigma ^{2})}$

Ocurrencia y aplicaciones

La aparición de una distribución normal en problemas prácticos se puede clasificar libremente en cuatro categorías:

Distribuciones exactamente normales;
Leyes aproximadamente normales, por ejemplo cuando dicha aproximación está justificada por el teorema del límite central ; y
Distribuciones modeladas como normales: la distribución normal es la distribución con máxima entropía para una media y varianza determinadas.
Problemas de regresión: la distribución normal se encuentra después de que los efectos sistemáticos se han modelado suficientemente bien.

Normalidad exacta

El estado fundamental de un oscilador armónico cuántico tiene la distribución gaussiana.

Algunas magnitudes físicas se distribuyen de forma normal, como demostró por primera vez James Clerk Maxwell . Algunos ejemplos de estas magnitudes son:

Función de densidad de probabilidad de un estado fundamental en un oscilador armónico cuántico .
La posición de una partícula que experimenta difusión . Si inicialmente la partícula está ubicada en un punto específico (es decir, su distribución de probabilidad es la función delta de Dirac ), entonces después del tiempo t su ubicación se describe mediante una distribución normal con varianza t , que satisface la ecuación de difusión . Si la ubicación inicial está dada por una cierta función de densidad , entonces la densidad en el tiempo t es la convolución de g y la función de densidad de probabilidad normal. ${\textstyle {\frac {\partial }{\partial t}}f(x,t)={\frac {1}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}f(x,t)}$ ${\textstyle g(x)}$

Normalidad aproximada

Las distribuciones aproximadamente normales se dan en muchas situaciones, como lo explica el teorema del límite central . Cuando el resultado es producido por muchos efectos pequeños que actúan de forma aditiva e independiente , su distribución será cercana a la normal. La aproximación normal no será válida si los efectos actúan de forma multiplicativa (en lugar de aditiva), o si hay una única influencia externa que tiene una magnitud considerablemente mayor que el resto de los efectos.

En problemas de conteo, donde el teorema del límite central incluye una aproximación de discreto a continuo y donde están involucradas distribuciones infinitamente divisibles y descomponibles , como
- Variables aleatorias binomiales , asociadas a variables de respuesta binarias;
- Variables aleatorias de Poisson , asociadas a eventos raros;
La radiación térmica tiene una distribución de Bose-Einstein en escalas de tiempo muy cortas y una distribución normal en escalas de tiempo más largas debido al teorema del límite central.

Supuesta normalidad

Sólo puedo reconocer la ocurrencia de la curva normal –la curva laplaciana de errores– como un fenómeno muy anormal. En ciertas distribuciones se la aproxima de forma aproximada; por esta razón, y debido a su hermosa simplicidad, tal vez podamos usarla como una primera aproximación, particularmente en investigaciones teóricas.
—Pearson (1901)

Existen métodos estadísticos para probar empíricamente esa suposición; consulte la sección Pruebas de normalidad más arriba.

En biología , los logaritmos de diversas variables tienden a tener una distribución normal, es decir, tienden a tener una distribución log-normal (después de la separación en subpoblaciones masculinas/femeninas), con ejemplos que incluyen:
- Medidas de tamaño de tejido vivo (longitud, altura, área de piel, peso); ^[53]
- La longitud de los apéndices inertes (pelo, garras, uñas, dientes) de especímenes biológicos, en la dirección del crecimiento ; presumiblemente, el grosor de la corteza de los árboles también entra en esta categoría;
- Ciertas medidas fisiológicas, como la presión arterial de los humanos adultos.
En finanzas, en particular en el modelo Black-Scholes , los cambios en el logaritmo de los tipos de cambio, índices de precios e índices bursátiles se suponen normales (estas variables se comportan como el interés compuesto , no como el interés simple, y por lo tanto son multiplicativas). Algunos matemáticos como Benoit Mandelbrot han argumentado que las distribuciones log-Levy , que poseen colas pesadas , serían un modelo más apropiado, en particular para el análisis de caídas del mercado bursátil . El uso del supuesto de distribución normal en los modelos financieros también ha sido criticado por Nassim Nicholas Taleb en sus obras.
Los errores de medición en los experimentos físicos suelen modelarse mediante una distribución normal. Este uso de una distribución normal no implica que se suponga que los errores de medición se distribuyen normalmente, sino que el uso de la distribución normal produce las predicciones más conservadoras posibles si solo se conoce la media y la varianza de los errores. ^[54]
En las pruebas estandarizadas , se puede lograr que los resultados tengan una distribución normal seleccionando el número y la dificultad de las preguntas (como en la prueba de CI ) o transformando las puntuaciones brutas de la prueba en puntuaciones de salida ajustándolas a la distribución normal. Por ejemplo, el rango tradicional de 200 a 800 del SAT se basa en una distribución normal con una media de 500 y una desviación estándar de 100.

Distribución normal acumulada ajustada a las precipitaciones de octubre, ver ajuste de distribución

Muchas puntuaciones se derivan de la distribución normal, incluidos los rangos de percentiles (percentiles o cuantiles), los equivalentes de curva normal , los estaninos , las puntuaciones z y las puntuaciones T. Además, algunos procedimientos estadísticos de comportamiento suponen que las puntuaciones se distribuyen normalmente; por ejemplo, las pruebas t y los ANOVA . La calificación de curva de campana asigna calificaciones relativas basadas en una distribución normal de puntuaciones.
En hidrología, la distribución de la descarga de un río o de las precipitaciones de larga duración, por ejemplo, los totales mensuales y anuales, suele considerarse prácticamente normal según el teorema del límite central . ^[55] La imagen azul, realizada con CumFreq , ilustra un ejemplo de ajuste de la distribución normal a las precipitaciones de octubre clasificadas que muestran el cinturón de confianza del 90 % basado en la distribución binomial . Los datos de precipitaciones se representan trazando posiciones como parte del análisis de frecuencia acumulada .

Problemas metodológicos y revisión por pares

John Ioannidis sostuvo que el uso de desviaciones típicas distribuidas normalmente como estándares para validar los hallazgos de una investigación deja sin probar predicciones falsables sobre fenómenos que no se distribuyen normalmente. Esto incluye, por ejemplo, fenómenos que solo aparecen cuando están presentes todas las condiciones necesarias y uno no puede ser un sustituto de otro de una manera similar a la adición y fenómenos que no se distribuyen aleatoriamente. Ioannidis sostiene que la validación centrada en la desviación típica da una falsa apariencia de validez a las hipótesis y teorías donde algunas, pero no todas, las predicciones falsables se distribuyen normalmente, ya que la parte de las predicciones falsables contra las que hay evidencia puede y en algunos casos se encuentra en las partes no distribuidas normalmente del rango de predicciones falsables, así como descartar sin fundamento hipótesis para las cuales ninguna de las predicciones falsables se distribuye normalmente como si fueran infalsables cuando, de hecho, sí hacen predicciones falsables. Ioannidis sostiene que muchos casos de teorías mutuamente excluyentes que son aceptadas como validadas por revistas de investigación se deben a que las revistas no aceptan falsificaciones empíricas de predicciones que no se distribuyen normalmente, y no a que las teorías mutuamente excluyentes sean verdaderas, lo cual no puede ser así, aunque dos teorías mutuamente excluyentes pueden ser erróneas y una tercera correcta. ^[56]

Métodos computacionales

Generación de valores a partir de una distribución normal

En las simulaciones por computadora, especialmente en las aplicaciones del método Monte-Carlo , a menudo es deseable generar valores que se distribuyan normalmente. Los algoritmos que se enumeran a continuación generan las desviaciones normales estándar, ya que una $N (μ, σ 2)$ se puede generar como $X = μ + σZ$ , donde Z es la normal estándar. Todos estos algoritmos se basan en la disponibilidad de un generador de números aleatorios U capaz de producir variables aleatorias uniformes .

El método más sencillo se basa en la propiedad de transformación integral de probabilidad : si U se distribuye uniformemente en (0,1), entonces Φ ⁻¹ ( U ) tendrá la distribución normal estándar. El inconveniente de este método es que se basa en el cálculo de la función probit Φ ⁻¹ , que no se puede realizar analíticamente. Algunos métodos aproximados se describen en Hart (1968) y en el artículo de erf . Wichura proporciona un algoritmo rápido para calcular esta función con 16 decimales, ^{[57] que}R utiliza para calcular variables aleatorias de la distribución normal.
Un enfoque aproximado fácil de programar que se basa en el teorema del límite central es el siguiente: generar 12 desviaciones uniformes U (0,1), sumarlas todas y restar 6: la variable aleatoria resultante tendrá aproximadamente una distribución normal estándar. En verdad, la distribución será Irwin-Hall , que es una aproximación polinómica de undécimo orden de 12 secciones a la distribución normal. Esta desviación aleatoria tendrá un rango limitado de (−6, 6). ^[58] Nótese que en una distribución normal verdadera, solo el 0,00034% de todas las muestras caerán fuera de ±6σ.
El método Box-Muller utiliza dos números aleatorios independientes U y V distribuidos uniformemente en (0,1). Entonces, las dos variables aleatorias X e Y tendrán ambas la distribución normal estándar y serán independientes . Esta formulación surge porque para un vector aleatorio normal bivariado ( X , Y ) la norma al cuadrado $X$ $2$ $+$ $Y$ $2$ tendrá la distribución chi-cuadrado con dos grados de libertad, que es una variable aleatoria exponencial fácilmente generada correspondiente a la cantidad −2 ln( U ) en estas ecuaciones; y el ángulo se distribuye uniformemente alrededor del círculo, elegido por la variable aleatoria V . $X={\sqrt {-2\ln U}}\,\cos(2\pi V),\qquad Y={\sqrt {-2\ln U}}\,\sin(2\pi V).$
El método polar de Marsaglia es una modificación del método de Box-Muller que no requiere el cálculo de las funciones seno y coseno. En este método, U y V se extraen de la distribución uniforme (−1,1) y luego se calcula $S = U 2 + V 2$ . Si S es mayor o igual a 1, entonces el método comienza de nuevo; de lo contrario, se devuelven las dos cantidades . Nuevamente, X e Y son variables aleatorias normales estándar independientes. $X=U{\sqrt {\frac {-2\ln S}{S}}},\qquad Y=V{\sqrt {\frac {-2\ln S}{S}}}$
El método de la proporción ^[59] es un método de rechazo. El algoritmo se desarrolla de la siguiente manera:
- Generar dos desviaciones uniformes independientes U y V ;
- Calcular X = √ 8/ e ( V − 0,5)/ U ;
- Opcional: si X ² ≤ 5 − 4 e ^1/4U entonces acepte X y finalice el algoritmo;
- Opcional: si X ² ≥ 4 e ^−1,35 / U + 1,4 entonces rechace X y comience nuevamente desde el paso 1;
- Si X ² ≤ −4 ln U entonces acepte X , de lo contrario comience nuevamente el algoritmo.
Los dos pasos opcionales permiten evitar en la mayoría de los casos la evaluación del logaritmo en el último paso. Estos pasos se pueden mejorar en gran medida ^[60] para que el logaritmo se evalúe con poca frecuencia.
El algoritmo del zigurat ^[61] es más rápido que la transformada de Box-Muller y sigue siendo exacto. En aproximadamente el 97% de los casos utiliza sólo dos números aleatorios, un entero aleatorio y un uniforme aleatorio, una multiplicación y una prueba condicional. Sólo en el 3% de los casos, cuando la combinación de esos dos números queda fuera del "núcleo del zigurat" (una especie de muestreo de rechazo que utiliza logaritmos), se deben emplear exponenciales y números aleatorios más uniformes.
La aritmética de enteros se puede utilizar para tomar muestras de la distribución normal estándar. ^[62] Este método es exacto en el sentido de que satisface las condiciones de aproximación ideal ; ^[63] es decir, es equivalente a tomar muestras de un número real de la distribución normal estándar y redondearlo al número de punto flotante representable más cercano.
También se han realizado algunas investigaciones ^[64] sobre la conexión entre la transformada rápida de Hadamard y la distribución normal, ya que la transformada emplea solo suma y resta y, por el teorema del límite central, los números aleatorios de casi cualquier distribución se transformarán en la distribución normal. En este sentido, una serie de transformadas de Hadamard se pueden combinar con permutaciones aleatorias para convertir conjuntos de datos arbitrarios en datos distribuidos normalmente.

Aproximaciones numéricas para la función de distribución acumulativa normal y la función cuantil normal

La función de distribución acumulativa normal estándar se utiliza ampliamente en la computación científica y estadística.

Los valores Φ( x ) pueden aproximarse con gran precisión mediante diversos métodos, como la integración numérica , la serie de Taylor , la serie asintótica y las fracciones continuas . Se utilizan diferentes aproximaciones según el nivel de precisión deseado.

Zelen y Severo (1964) dan la aproximación para Φ( x ) para x > 0 con el error absoluto $| ε (x) | < 7.5\cdot10 -8$ (algoritmo 26.2.17): donde ϕ ( x ) es la función de densidad de probabilidad normal estándar, y b ₀ = 0.2316419, b ₁ = 0.319381530, b ₂ = −0.356563782, b ₃ = 1.781477937, b ₄ = −1.821255978, b ₅ = 1.330274429. $\Phi (x)=1-\varphi (x)\left(b_{1}t+b_{2}t^{2}+b_{3}t^{3}+b_{4}t^{4}+b_{5}t^{5}\right)+\varepsilon (x),\qquad t={\frac {1}{1+b_{0}x}},$
Hart (1968) enumera algunas docenas de aproximaciones –mediante funciones racionales, con o sin exponenciales– para la función erfc() . Sus algoritmos varían en el grado de complejidad y la precisión resultante, con una precisión absoluta máxima de 24 dígitos. Un algoritmo de West (2009) combina el algoritmo 5666 de Hart con una aproximación de fracción continua en la cola para proporcionar un algoritmo de cálculo rápido con una precisión de 16 dígitos.
Cody (1969), después de recordar que la solución Hart68 no es adecuada para erf, proporciona una solución tanto para erf como para erfc, con un límite de error relativo máximo, a través de la aproximación racional de Chebyshev .
Marsaglia (2004) sugirió un algoritmo simple ^{[nota 1]} basado en la expansión de la serie de Taylor para calcular $Φ($ $x$ $)$ con precisión arbitraria. La desventaja de este algoritmo es el tiempo de cálculo comparativamente lento (por ejemplo, se necesitan más de 300 iteraciones para calcular la función con 16 dígitos de precisión cuando $x$ $= 10$ ). $\Phi (x)={\frac {1}{2}}+\varphi (x)\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{3\cdot 5}}+{\frac {x^{7}}{3\cdot 5\cdot 7}}+{\frac {x^{9}}{3\cdot 5\cdot 7\cdot 9}}+\cdots \right)$
La Biblioteca Científica GNU calcula valores de la función de distribución acumulativa normal estándar utilizando los algoritmos de Hart y aproximaciones con polinomios de Chebyshev .
Dia (2023) propone la siguiente aproximación de con un error relativo máximo menor que en valor absoluto: para y para , ${\textstyle 1-\Phi }$ ${\textstyle 2^{-53}}$ ${\textstyle \left(\approx 1.1\times 10^{-16}\right)}$ ${\textstyle x\geq 0}$ ${\textstyle {\begin{aligned}1-\Phi \left(x\right)&=\left({\frac {0.39894228040143268}{x+2.92678600515804815}}\right)\left({\frac {x^{2}+8.42742300458043240x+18.38871225773938487}{x^{2}+5.81582518933527391x+8.97280659046817350}}\right)\\&\left({\frac {x^{2}+7.30756258553673541x+18.25323235347346525}{x^{2}+5.70347935898051437x+10.27157061171363079}}\right)\left({\frac {x^{2}+5.66479518878470765x+18.61193318971775795}{x^{2}+5.51862483025707963x+12.72323261907760928}}\right)\\&\left({\frac {x^{2}+4.91396098895240075x+24.14804072812762821}{x^{2}+5.26184239579604207x+16.88639562007936908}}\right)\left({\frac {x^{2}+3.83362947800146179x+11.61511226260603247}{x^{2}+4.92081346632882033x+24.12333774572479110}}\right)e^{-{\frac {x^{2}}{2}}}\end{aligned}}}$ ${\textstyle x<0}$

$1-\Phi \left(x\right)=1-\left(1-\Phi \left(-x\right)\right)$

Shore (1982) introdujo aproximaciones simples que pueden incorporarse en modelos de optimización estocástica de ingeniería e investigación de operaciones, como la ingeniería de confiabilidad y el análisis de inventarios. Denotando $p = Φ(z)$ , la aproximación más simple para la función cuantil es: $z=\Phi ^{-1}(p)=5.5556\left[1-\left({\frac {1-p}{p}}\right)^{0.1186}\right],\qquad p\geq 1/2$

Esta aproximación proporciona para z un error absoluto máximo de 0,026 (para $0,5 \leq p \leq 0,9999$ , correspondiente a $0 \leq z \leq 3,719$ ). Para $p < 1/2,$ sustituya p por $1 - p$ y cambie el signo. Otra aproximación, algo menos precisa, es la aproximación de un solo parámetro: $z=-0.4115\left\{{\frac {1-p}{p}}+\log \left[{\frac {1-p}{p}}\right]-1\right\},\qquad p\geq 1/2$

Este último había servido para derivar una aproximación simple para la integral de pérdida de la distribución normal, definida por ${\begin{aligned}L(z)&=\int _{z}^{\infty }(u-z)\varphi (u)\,du=\int _{z}^{\infty }[1-\Phi (u)]\,du\\[5pt]L(z)&\approx {\begin{cases}0.4115\left({\dfrac {p}{1-p}}\right)-z,&p<1/2,\\\\0.4115\left({\dfrac {1-p}{p}}\right),&p\geq 1/2.\end{cases}}\\[5pt]{\text{or, equivalently,}}\\L(z)&\approx {\begin{cases}0.4115\left\{1-\log \left[{\frac {p}{1-p}}\right]\right\},&p<1/2,\\\\0.4115{\dfrac {1-p}{p}},&p\geq 1/2.\end{cases}}\end{aligned}}$

Esta aproximación es particularmente precisa para la cola lejana derecha (error máximo de 10 ⁻³ para z ≥ 1,4). En Shore (2005) se muestran aproximaciones de alta precisión para la función de distribución acumulativa, basadas en la metodología de modelado de respuesta (RMM, Shore, 2011, 2012).

Se pueden encontrar más aproximaciones en: Función de error#Aproximación con funciones elementales . En particular, un pequeño error relativo en todo el dominio para la función de distribución acumulativa y también para la función cuantil se logra mediante una fórmula explícitamente invertible de Sergei Winitzki en 2008. ${\textstyle \Phi }$ ${\textstyle \Phi ^{-1}}$

Historia

Desarrollo

Algunos autores ^[65]^[66] atribuyen el crédito por el descubrimiento de la distribución normal a de Moivre , quien en 1738 ^{[nota 2]} publicó en la segunda edición de su La doctrina de las probabilidades el estudio de los coeficientes en la expansión binomial de $(a + b) n$ . De Moivre demostró que el término medio en esta expansión tiene la magnitud aproximada de , y que "Si m o ⁠ ${\textstyle 2^{n}/{\sqrt {2\pi n}}}$ 1/2n sea una cantidad infinitamente grande, entonces el logaritmo de la razón que un término distante de la mitad por el intervalo ℓ tiene con el término medio, es ." ^[67] Aunque este teorema puede interpretarse como la primera expresión oscura para la ley de probabilidad normal, Stigler señala que el propio de Moivre no interpretó sus resultados como nada más que la regla aproximada para los coeficientes binomiales, y en particular de Moivre carecía del concepto de la función de densidad de probabilidad. ^[68] ${\textstyle -{\frac {2\ell \ell }{n}}}$

En 1823 Gauss publicó su monografía " Theoria combinationis observationum erroribus minimis obnoxiae " donde entre otras cosas introduce varios conceptos estadísticos importantes, como el método de mínimos cuadrados , el método de máxima verosimilitud y la distribución normal . Gauss utilizó M , M ′ , M ′′, ... para denotar las mediciones de alguna cantidad desconocida V , y buscó el estimador más probable de esa cantidad: el que maximiza la probabilidad $φ (M - V) \cdot φ (M' - V) \cdot φ (M'' - V) \cdot ...$ de obtener los resultados experimentales observados. En su notación φΔ es la función de densidad de probabilidad de los errores de medición de magnitud Δ. Al no saber cuál es la función φ , Gauss requiere que su método se reduzca a la respuesta bien conocida: la media aritmética de los valores medidos. ^{[nota 3]} Partiendo de estos principios, Gauss demuestra que la única ley que racionaliza la elección de la media aritmética como estimador del parámetro de localización es la ley normal de los errores: ^[69] donde h es “la medida de la precisión de las observaciones”. Utilizando esta ley normal como modelo genérico de los errores en los experimentos, Gauss formula lo que hoy se conoce como el método de mínimos cuadrados ponderados no lineales . ^[70] $\varphi {\mathit {\Delta }}={\frac {h}{\surd \pi }}\,e^{-\mathrm {hh} \Delta \Delta },$

Aunque Gauss fue el primero en sugerir la ley de distribución normal, Laplace hizo contribuciones significativas. ^{[nota 4]} Fue Laplace quien primero planteó el problema de agregar varias observaciones en 1774, ^[71] aunque su propia solución condujo a la distribución laplaciana . Fue Laplace quien primero calculó el valor de la integral ∫ e ^{− t ²} dt = √ $π$ en 1782, proporcionando la constante de normalización para la distribución normal. ^[72] Por este logro, Gauss reconoció la prioridad de Laplace. ^[73] Finalmente, fue Laplace quien en 1810 demostró y presentó a la academia el teorema fundamental del límite central , que enfatizó la importancia teórica de la distribución normal. ^[74]

Es interesante señalar que en 1809 el matemático estadounidense de origen irlandés Robert Adrain publicó dos derivaciones perspicaces pero defectuosas de la ley de probabilidad normal, simultánea e independientemente de Gauss. ^[75] Sus obras pasaron en gran medida desapercibidas para la comunidad científica, hasta que en 1871 fueron exhumadas por Abbe . ^[76]

A mediados del siglo XIX, Maxwell demostró que la distribución normal no es sólo una herramienta matemática conveniente, sino que también puede ocurrir en fenómenos naturales: ^[77] El número de partículas cuya velocidad, resuelta en una dirección determinada, se encuentra entre x y x + dx es $\operatorname {N} {\frac {1}{\alpha \;{\sqrt {\pi }}}}\;e^{-{\frac {x^{2}}{\alpha ^{2}}}}\,dx$

Nombramiento

En la actualidad, el concepto se conoce generalmente en inglés como distribución normal o distribución gaussiana . Otros nombres menos comunes incluyen distribución de Gauss, distribución de Laplace-Gauss, ley del error, ley de la facilidad de errores, segunda ley de Laplace y ley gaussiana.

El propio Gauss aparentemente acuñó el término con referencia a las "ecuaciones normales" involucradas en sus aplicaciones, teniendo el término normal su significado técnico de ortogonal en lugar de habitual. ^[78] Sin embargo, a fines del siglo XIX algunos autores ^{[nota 5]} habían comenzado a usar el nombre de distribución normal , donde la palabra "normal" se usaba como adjetivo; el término ahora se considera un reflejo del hecho de que esta distribución se consideraba típica, común y, por lo tanto, normal. Peirce (uno de esos autores) una vez definió "normal" de esta manera: "... lo 'normal' no es el promedio (o cualquier otro tipo de media) de lo que realmente ocurre, sino de lo que , a largo plazo, ocurriría bajo ciertas circunstancias". ^[79] A principios del siglo XX, Pearson popularizó el término normal como una designación para esta distribución. ^[80]

Hace muchos años llamé a la curva de Laplace-Gauss la curva normal , nombre que, si bien evita una cuestión internacional de prioridad, tiene la desventaja de llevar a la gente a creer que todas las demás distribuciones de frecuencia son en un sentido u otro "anormales".
—Pearson (1920)

Además, fue Pearson quien primero escribió la distribución en términos de la desviación típica σ, tal como se utiliza en la notación moderna. Poco después, en el año 1915, Fisher agregó el parámetro de ubicación a la fórmula de la distribución normal, expresándola de la manera en que se escribe actualmente: $df={\frac {1}{\sqrt {2\sigma ^{2}\pi }}}e^{-(x-m)^{2}/(2\sigma ^{2})}\,dx.$

El término "normal estándar", que denota la distribución normal con media cero y varianza unitaria, comenzó a usarse de manera generalizada alrededor de los años 1950, apareciendo en los populares libros de texto de P. G. Hoel (1947) Introducción a la estadística matemática y A. M. Mood (1950) Introducción a la teoría de la estadística . ^[81]

Véase también

Distribución de Bates : similar a la distribución de Irwin-Hall, pero reescalada al rango de 0 a 1
Problema de Behrens-Fisher : el antiguo problema de probar si dos muestras normales con diferentes varianzas tienen las mismas medias;
Distancia de Bhattacharyya : método utilizado para separar mezclas de distribuciones normales
Teorema de Erdős-Kac : sobre la aparición de la distribución normal en la teoría de números
Ancho completo a la mitad máximo
Desenfoque gaussiano – convolución , que utiliza la distribución normal como núcleo
La distribución seminormal modificada ^[82] con la función de densidad de probabilidad activada se da como , donde denota la función Psi de Fox–Wright . ${\textstyle (0,\infty )}$ ${\textstyle f(x)={\frac {2\beta ^{\frac {\alpha }{2}}x^{\alpha -1}\exp(-\beta x^{2}+\gamma x)}{\Psi {\left({\frac {\alpha }{2}},{\frac {\gamma }{\sqrt {\beta }}}\right)}}}}$ ${\textstyle \Psi (\alpha ,z)={}_{1}\Psi _{1}\left({\begin{matrix}\left(\alpha ,{\frac {1}{2}}\right)\\(1,0)\end{matrix}};z\right)}$
Distribuido normalmente y no correlacionado no implica independencia
Distribución normal de proporciones
Distribución normal recíproca
Tabla normal estándar
Lema de Stein
Distribución subgaussiana
Suma de variables aleatorias distribuidas normalmente
Distribución Tweedie – La distribución normal es un miembro de la familia de modelos de dispersión exponencial Tweedie .
Distribución normal envuelta : la distribución normal aplicada a un dominio circular
Prueba Z : uso de la distribución normal

Notas

^ Por ejemplo, este algoritmo se da en el artículo Lenguaje de programación Bc .
↑ De Moivre publicó por primera vez sus hallazgos en 1733, en un folleto Approximatio ad Summam Terminorum Binomii $($ a + b ).norteen Seriem Expansi , que estaba destinada únicamente a la circulación privada. Pero no fue hasta el año 1738 cuando hizo públicos sus resultados. El folleto original se reimprimió varias veces, véase por ejemplo Walker (1985).
^ "Se ha acostumbrado, sin duda, a considerar como un axioma la hipótesis de que si una cantidad ha sido determinada por varias observaciones directas, realizadas en las mismas circunstancias y con el mismo cuidado, la media aritmética de los valores observados proporciona el valor más probable, si no rigurosamente, al menos muy cerca, de modo que siempre es más seguro adherirse a ella." — Gauss (1809, sección 177)
^ "Mi costumbre de denominar a esta curva como curva de Gauss-Laplaciana o curva normal nos ahorra la tarea de medir el mérito del descubrimiento entre los dos grandes astrónomos matemáticos". cita de Pearson (1905, p. 189)
^ Además de aquellos específicamente referenciados aquí, dicho uso se encuentra en las obras de Peirce , Galton (Galton (1889, capítulo V)) y Lexis (Lexis (1878), Rohrbasser & Véron (2003)) c. 1875. ^{[ cita requerida ]}

Referencias

Citas

^ Norton, Matthew; Khokhlov, Valentyn; Uryasev, Stan (2019). "Cálculo de CVaR y bPOE para distribuciones de probabilidad comunes con aplicación a la optimización de carteras y estimación de densidad" (PDF) . Anales de investigación de operaciones . 299 (1–2). Springer: 1281–1315. arXiv : 1811.11301 . doi :10.1007/s10479-019-03373-1. S2CID 254231768. Archivado desde el original (PDF) el 31 de marzo de 2023 . Consultado el 27 de febrero de 2023 .
^ Distribución normal, Enciclopedia Gale de Psicología
^ Casella y Berger (2001, pág. 102)
^ Lyon, A. (2014). ¿Por qué las distribuciones normales son normales?, The British Journal for the Philosophy of Science.
^ Jorge, Nocedal; Stephan, J. Wright (2006). Optimización numérica (2.ª ed.). Springer. pág. 249. ISBN 978-0387-30303-1.
^ ab "Distribución normal". www.mathsisfun.com . Consultado el 15 de agosto de 2020 .
^ Stigler (1982)
^ Halperin, Hartley y Hoel (1965, artículo 7)
^ McPherson (1990, pág. 110)
^ Bernardo y Smith (2000, pág. 121)
^ Scott, Clayton; Nowak, Robert (7 de agosto de 2003). "La función Q". Connexions .
^ Barak, Ohad (6 de abril de 2006). "Función Q y función de error" (PDF) . Universidad de Tel Aviv. Archivado desde el original (PDF) el 25 de marzo de 2009.
^ Weisstein, Eric W. "Función de distribución normal". MathWorld .
^ Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [junio de 1964]. "Capítulo 26, ecuación 26.2.12". Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas . Serie de Matemáticas Aplicadas. Vol. 55 (Novena reimpresión con correcciones adicionales de la décima impresión original con correcciones (diciembre de 1972); primera ed.). Washington DC; Nueva York: Departamento de Comercio de los Estados Unidos, Oficina Nacional de Normas; Dover Publications. pág. 932. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
^ Vaart, AW van der (13 de octubre de 1998). Estadística asintótica. Cambridge University Press. doi :10.1017/cbo9780511802256. ISBN 978-0-511-80225-6.
^ Portada, Thomas M.; Thomas, Joy A. (2006). Elementos de la teoría de la información . John Wiley and Sons. pág. 254. ISBN 9780471748816.
^ Park, Sung Y.; Bera, Anil K. (2009). "Maximum Entropy Autoregressive Conditional Heteroskedasticity Model" (PDF) . Revista de Econometría . 150 (2): 219–230. CiteSeerX 10.1.1.511.9750 . doi :10.1016/j.jeconom.2008.12.014. Archivado desde el original (PDF) el 7 de marzo de 2016 . Consultado el 2 de junio de 2011 .
^ Geary RC (1936) La distribución del "cociente de Student para las muestras no normales". Suplemento del Journal of the Royal Statistical Society 3 (2): 178–184
^ Lukacs, Eugene (marzo de 1942). "Una caracterización de la distribución normal". Anales de estadística matemática . 13 (1): 91–93. doi :10.1214/AOMS/1177731647. ISSN 0003-4851. JSTOR 2236166. MR 0006626. Zbl 0060.28509. Wikidata Q55897617.
^ abc Patel y Read (1996, [2.1.4])
^ Fan (1991, pág. 1258)
^ Patel y Read (1996, [2.1.8])
^ Papoulis, Athanasios. Probabilidad, variables aleatorias y procesos estocásticos (4ª ed.). pág. 148.
^ Winkelbauer, Andreas (2012). "Momentos y momentos absolutos de la distribución normal". arXiv : 1209.4340 [math.ST].
^ Bryc (1995, pág. 23)
^ Bryc (1995, pág. 24)
^ Cover y Thomas (2006, pág. 254)
^ Williams, David (2001). Weighing the odds : a course in probability and statistics (Ed. reimpresa). Cambridge [ua]: Cambridge Univ. Press. págs. 197–199. ISBN 978-0-521-00618-7.
^ Smith, José M. Bernardo; Adrian FM (2000). Teoría bayesiana (edición reimpresa). Chichester [ua]: Wiley. pp. 209, 366. ISBN 978-0-471-49464-5.{{cite book}}: CS1 maint: multiple names: authors list (link)
^ O'Hagan, A. (1994) Kendall's Advanced Theory of statistics, vol. 2B, Inferencia bayesiana , Edward Arnold. ISBN 0-340-52922-9 (sección 5.40)
^ de Bryc (1995, pág. 35)
^ UIUC, Clase 21. La distribución normal multivariante, 21.6: "Gaussiana individual versus gaussiana conjunta".
^ Edward L. Melnick y Aaron Tenenbein, "Errores de especificación de la distribución normal", The American Statistician , volumen 36, número 4, noviembre de 1982, páginas 372-373
^ "Distancia de Kullback Leibler (KL) de dos distribuciones de probabilidad normales (gaussianas)". Allisons.org . 5 de diciembre de 2007 . Consultado el 3 de marzo de 2017 .
^ Jordan, Michael I. (8 de febrero de 2010). "Stat260: Modelado e inferencia bayesianos: la distribución conjugada previa para la distribución normal" (PDF) .
^ Amari y Nagaoka (2000)
^ "Esperanza del máximo de variables aleatorias gaussianas". Mathematics Stack Exchange . Consultado el 7 de abril de 2024 .
^ "Aproximación normal a la distribución de Poisson". Stat.ucla.edu . Consultado el 3 de marzo de 2017 .
^ ab Das, Abhranil (2021). "Un método para integrar y clasificar distribuciones normales". Journal of Vision . 21 (10): 1. arXiv : 2012.14331 . doi :10.1167/jov.21.10.1. PMC 8419883 . PMID 34468706.
^ Bryc (1995, pág. 27)
^ Weisstein, Eric W. "Distribución normal del producto". MathWorld . wolfram.com.
^ Lukacs, Eugene (1942). "Una caracterización de la distribución normal". Anales de estadística matemática . 13 (1): 91–3. doi : 10.1214/aoms/1177731647 . ISSN 0003-4851. JSTOR 2236166.
^ Basu, D.; Laha, RG (1954). "Sobre algunas caracterizaciones de la distribución normal". Sankhyā . 13 (4): 359–62. ISSN 0036-4452. JSTOR 25048183.
^ Lehmann, EL (1997). Prueba de hipótesis estadísticas (2.ª ed.). Springer. pág. 199. ISBN 978-0-387-94919-2.
^ Patel y Read (1996, [2.3.6])
^ Galambos y Simonelli (2004, teorema 3.5)
^ de Lukacs y King (1954)
^ Quine, MP (1993). "Sobre tres caracterizaciones de la distribución normal". Probabilidad y estadística matemática . 14 (2): 257–263.
^ John, S (1982). "La familia de distribuciones normales de dos piezas y tres parámetros y su ajuste". Communications in Statistics – Theory and Methods . 11 (8): 879–885. doi :10.1080/03610928208828279.
^ por Krishnamoorthy (2006, pág. 127)
^ Krishnamoorthy (2006, pág. 130)
^ Krishnamoorthy (2006, pág. 133)
^ Huxley (1932)
^ Jaynes, Edwin T. (2003). Teoría de la probabilidad: la lógica de la ciencia. Cambridge University Press. pp. 592–593. ISBN 9780521592710.
^ Oosterbaan, Roland J. (1994). "Capítulo 6: Análisis de frecuencia y regresión de datos hidrológicos" (PDF) . En Ritzema, Henk P. (ed.). Principios y aplicaciones del drenaje, publicación 16 (segunda edición revisada). Wageningen, Países Bajos: Instituto Internacional para la Recuperación y Mejora de Tierras (ILRI). pp. 175–224. ISBN 978-90-70754-33-4.
^ Por qué la mayoría de los resultados de las investigaciones publicadas son falsos, John PA Ioannidis, 2005
^ Wichura, Michael J. (1988). "Algoritmo AS241: Los puntos porcentuales de la distribución normal". Applied Statistics . 37 (3): 477–84. doi :10.2307/2347330. JSTOR 2347330.
^ Johnson, Kotz y Balakrishnan (1995, Ecuación (26.48))
^ Kinderman y Monahan (1977)
^ Leva (1992)
^ Marsaglia y Tsang (2000)
^ Karney (2016)
^ Monahan (1985, sección 2)
^ Wallace (1996)
^ Johnson, Kotz y Balakrishnan (1994, pág. 85)
^ Le Cam y Lo Yang (2000, pág.74)
^ De Moivre, Abraham (1733), Corolario I – véase Walker (1985, p. 77)
^ Stigler (1986, pág. 76)
^ Gauss (1809, sección 177)
^ Gauss (1809, sección 179)
^ Laplace (1774, Problema III)
^ Pearson (1905, pág. 189)
^ Gauss (1809, sección 177)
^ Stigler (1986, pág. 144)
^ Stigler (1978, pág. 243)
^ Stigler (1978, pág. 244)
^ Maxwell (1860, pág. 23)
^ Jaynes, Edwin J.; Teoría de la probabilidad: la lógica de la ciencia , cap. 7.
^ Peirce, Charles S. (c. 1909 MS), Collected Papers v. 6, párrafo 327.
^ Kruskal y Stigler (1997).
^ "Usos más tempranos... (Curva normal estándar de entrada)".
^ Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 de junio de 2021). "La distribución modificada-semi-normal: propiedades y un esquema de muestreo eficiente". Comunicaciones en Estadística – Teoría y Métodos . 52 (5): 1591–1613. doi :10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.

Fuentes

Aldrich, John; Miller, Jeff. "Los primeros usos de los símbolos en probabilidad y estadística".
Aldrich, John; Miller, Jeff. "Los primeros usos conocidos de algunas de las palabras de las matemáticas".En particular, las entradas para "campana y curva de campana", "normal (distribución)", "gaussiana" y "Error, ley del error, teoría de errores, etc.".
Amari, Shun-ichi; Nagaoka, Hiroshi (2000). Métodos de geometría de la información . Oxford University Press. ISBN 978-0-8218-0531-2.
Bernardo, José M.; Smith, Adrian FM (2000). Teoría bayesiana . Wiley. ISBN 978-0-471-49464-5.
Bryc, Wlodzimierz (1995). La distribución normal: caracterizaciones con aplicaciones . Springer-Verlag. ISBN 978-0-387-97990-8.
Casella, George; Berger, Roger L. (2001). Inferencia estadística (2.ª ed.). Duxbury. ISBN 978-0-534-24312-8.
Cody, William J. (1969). "Aproximaciones racionales de Chebyshev para la función de error" . Matemáticas de la computación . 23 (107): 631–638. doi : 10.1090/S0025-5718-1969-0247736-4 .
Portada, Thomas M.; Thomas, Joy A. (2006). Elementos de la teoría de la información . John Wiley and Sons.
Dia, Yaya D. (2023). "Integrales incompletas aproximadas, aplicación a la función de error complementaria". SSRN . doi :10.2139/ssrn.4487559. S2CID 259689086.
de Moivre, Abraham (1738). La doctrina de las probabilidades . Sociedad Matemática Americana. ISBN 978-0-8218-2103-9.
Fan, Jianqing (1991). "Sobre las tasas óptimas de convergencia para problemas de deconvolución no paramétricos". Anales de Estadística . 19 (3): 1257–1272. doi : 10.1214/aos/1176348248 . JSTOR 2241949.
Galton, Francis (1889). Herencia natural (PDF) . Londres, Reino Unido: Richard Clay and Sons.
Galambos, Janos; Simonelli, Italo (2004). Productos de variables aleatorias: aplicaciones a problemas de física y funciones aritméticas . Marcel Dekker, Inc. ISBN 978-0-8247-5402-0.
Gauss, Carolo Friderico (1809). Theoria motvs corporvm coelestivm in sectionibvs conicis Solem ambientivm [ Teoría del movimiento de los cuerpos celestes que se mueven alrededor del Sol en secciones cónicas ] (en latín). Hambvrgi, Svmtibvs F. Perthes et IH Besser. Traducción al inglés.
Gould, Stephen Jay (1981). La falsa medida del hombre (primera edición). WW Norton. ISBN 978-0-393-01489-1.
Halperin, Max; Hartley, Herman O.; Hoel, Paul G. (1965). "Estándares recomendados para símbolos y notación estadística. Comité COPSS sobre símbolos y notación". El estadístico estadounidense . 19 (3): 12–14. doi :10.2307/2681417. JSTOR 2681417.
Hart, John F.; et al. (1968). Aproximaciones informáticas . Nueva York, Nueva York: John Wiley & Sons, Inc. ISBN 978-0-88275-642-4.
"Distribución normal", Enciclopedia de matemáticas , EMS Press , 2001 [1994]
Herrnstein, Richard J.; Murray, Charles (1994). La curva de campana: inteligencia y estructura de clases en la vida estadounidense . Free Press . ISBN 978-0-02-914673-6.
Huxley, Julian S. (1932). Problemas de crecimiento relativo . Londres. ISBN 978-0-486-61114-3.OCLC 476909537 .
Johnson, Norman L.; Kotz, Samuel; Balakrishnan, Narayanaswamy (1994). Distribuciones univariadas continuas, volumen 1. Wiley. ISBN 978-0-471-58495-7.
Johnson, Norman L.; Kotz, Samuel; Balakrishnan, Narayanaswamy (1995). Distribuciones univariadas continuas, volumen 2. Wiley. ISBN 978-0-471-58494-0.
Karney, CFF (2016). "Muestreo exacto a partir de la distribución normal". ACM Transactions on Mathematical Software . 42 (1): 3:1–14. arXiv : 1303.6257 . doi :10.1145/2710016. S2CID 14252035.
Kinderman, Albert J.; Monahan, John F. (1977). "Generación informática de variables aleatorias utilizando la proporción de desviaciones uniformes". ACM Transactions on Mathematical Software . 3 (3): 257–260. doi : 10.1145/355744.355750 . S2CID 12884505.
Krishnamoorthy, Kalimuthu (2006). Manual de distribuciones estadísticas con aplicaciones . Chapman & Hall/CRC. ISBN 978-1-58488-635-8.
Kruskal, William H.; Stigler, Stephen M. (1997). Spencer, Bruce D. (ed.). Terminología normativa: "normal" en estadística y en otros ámbitos . Estadística y política pública. Oxford University Press. ISBN 978-0-19-852341-3.
Laplace, Pierre-Simon de (1774). "Mémoire sur la probabilité des cause par les événements". Mémoires de l'Académie Royale des Sciences de Paris (Savants étrangers), Tomo 6 : 621–656.Traducido por Stephen M. Stigler en Statistical Science 1 (3), 1986: JSTOR 2245476.
Laplace, Pierre-Simon (1812). Théorie analytique des probabilités [ Teoría analítica de las probabilidades ]. París, Ve. Mensajero.
Le Cam, Lucien; Lo Yang, Grace (2000). Asintótica en estadística: algunos conceptos básicos (segunda edición). Springer. ISBN 978-0-387-95036-5.
Leva, Joseph L. (1992). "Un generador rápido de números aleatorios normales" (PDF) . ACM Transactions on Mathematical Software . 18 (4): 449–453. CiteSeerX 10.1.1.544.5806 . doi :10.1145/138351.138364. S2CID 15802663. Archivado desde el original (PDF) el 16 de julio de 2010.
Léxis, Wilhelm (1878). "Sobre la duración normal de la vida humana y sobre la teoría de la estabilidad de las relaciones estadísticas". Annales de Démographie Internationale . II . París: 447–462.
Lukacs, Eugene; King, Edgar P. (1954). "Una propiedad de la distribución normal". Anales de estadística matemática . 25 (2): 389–394. doi : 10.1214/aoms/1177728796 . JSTOR 2236741.
McPherson, Glen (1990). Estadística en la investigación científica: su base, aplicación e interpretación . Springer-Verlag. ISBN 978-0-387-97137-7.
Marsaglia, George ; Tsang, Wai Wan (2000). "El método Ziggurat para generar variables aleatorias". Journal of Statistical Software . 5 (8). doi : 10.18637/jss.v005.i08 .
Marsaglia, George (2004). "Evaluación de la distribución normal". Revista de software estadístico . 11 (4). doi : 10.18637/jss.v011.i04 .
Maxwell, James Clerk (1860). «V. Ilustraciones de la teoría dinámica de los gases. — Parte I: Sobre los movimientos y colisiones de esferas perfectamente elásticas». Revista filosófica . Serie 4. 19 (124): 19–32. doi :10.1080/14786446008642818.
Monahan, JF (1985). "Precisión en la generación de números aleatorios". Matemáticas de la computación . 45 (172): 559–568. doi : 10.1090/S0025-5718-1985-0804945-X .
Patel, Jagdish K.; Read, Campbell B. (1996). Manual de la distribución normal (2.ª edición). CRC Press. ISBN 978-0-8247-9342-5.
Pearson, Karl (1901). "Sobre líneas y planos de ajuste más cercano a sistemas de puntos en el espacio" (PDF) . Philosophical Magazine . 6. 2 (11): 559–572. doi :10.1080/14786440109462720. S2CID 125037489.
Pearson, Karl (1905). "'Das Fehlergesetz und seine Verallgemeinerungen durch Fechner und Pearson'. Una réplica". Biometrika . 4 (1): 169–212. doi :10.2307/2331536. JSTOR 2331536.
Pearson, Karl (1920). "Notas sobre la historia de la correlación". Biometrika . 13 (1): 25–45. doi :10.1093/biomet/13.1.25. JSTOR 2331722.
Rohrbasser, Jean-Marc; Véron, Jacques (2003). "Wilhelm Lexis: La duración normal de la vida como expresión de la "naturaleza de las cosas"". Población . 58 (3): 303–322. doi : 10.3917/pope.303.0303 .
Shore, H (1982). "Aproximaciones simples para la función acumulativa inversa, la función de densidad y la integral de pérdida de la distribución normal". Revista de la Royal Statistical Society. Serie C (Estadística aplicada) . 31 (2): 108–114. doi :10.2307/2347972. JSTOR 2347972.
Shore, H (2005). "Aproximaciones precisas basadas en RMM para la CDF de la distribución normal". Communications in Statistics – Theory and Methods . 34 (3): 507–513. doi :10.1081/sta-200052102. S2CID 122148043.
Shore, H (2011). "Metodología de modelado de respuesta". WIREs Comput Stat . 3 (4): 357–372. doi :10.1002/wics.151. S2CID 62021374.
Shore, H (2012). "Metodología de estimación de modelos de modelado de respuesta". WIREs Comput Stat . 4 (3): 323–333. doi :10.1002/wics.1199. S2CID 122366147.
Stigler, Stephen M. (1978). "Estadística matemática en los primeros tiempos". Anales de estadística . 6 (2): 239–265. doi : 10.1214/aos/1176344123 . JSTOR 2958876.
Stigler, Stephen M. (1982). "Una propuesta modesta: un nuevo estándar para lo normal". The American Statistician . 36 (2): 137–138. doi :10.2307/2684031. JSTOR 2684031.
Stigler, Stephen M. (1986). Historia de la estadística: la medición de la incertidumbre antes de 1900. Harvard University Press. ISBN 978-0-674-40340-6.
Stigler, Stephen M. (1999). Estadísticas sobre la tabla . Harvard University Press. ISBN 978-0-674-83601-3.
Walker, Helen M. (1985). "De Moivre sobre la ley de probabilidad normal" (PDF) . En Smith, David Eugene (ed.). Un libro de consulta sobre matemáticas . Dover. ISBN 978-0-486-64690-9.
Wallace, CS (1996). "Generadores pseudoaleatorios rápidos para variables normales y exponenciales". ACM Transactions on Mathematical Software . 22 (1): 119–127. doi : 10.1145/225545.225554 . S2CID 18514848.
Weisstein, Eric W. "Distribución normal". MundoMatemático .
West, Graeme (2009). "Mejores aproximaciones a funciones normales acumulativas" (PDF) . Wilmott Magazine : 70–76. Archivado desde el original (PDF) el 29 de febrero de 2012.
Zelen, Marvin; Severo, Norman C. (1964). Funciones de probabilidad (capítulo 26). Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas , por Abramowitz, M .; y Stegun, IA : National Bureau of Standards. Nueva York, NY: Dover. ISBN 978-0-486-61272-0.

Enlaces externos

"Distribución normal", Enciclopedia de Matemáticas , EMS Press , 2001 [1994]
Calculadora de distribución normal

[65] Por ejemplo, este algoritmo se da en el artículo Lenguaje de programación Bc .

[68] De Moivre publicó por primera vez sus hallazgos en 1733, en un folleto Approximatio ad Summam Terminorum Binomii $($ a + b ).norteen Seriem Expansi , que estaba destinada únicamente a la circulación privada. Pero no fue hasta el año 1738 cuando hizo públicos sus resultados. El folleto original se reimprimió varias veces, véase por ejemplo Walker (1985).

[71] "Se ha acostumbrado, sin duda, a considerar como un axioma la hipótesis de que si una cantidad ha sido determinada por varias observaciones directas, realizadas en las mismas circunstancias y con el mismo cuidado, la media aritmética de los valores observados proporciona el valor más probable, si no rigurosamente, al menos muy cerca, de modo que siempre es más seguro adherirse a ella." — Gauss (1809, sección 177)

[74] "Mi costumbre de denominar a esta curva como curva de Gauss-Laplaciana o curva normal nos ahorra la tarea de medir el mérito del descubrimiento entre los dos grandes astrónomos matemáticos". cita de Pearson (1905, p. 189)

[83] Además de aquellos específicamente referenciados aquí, dicho uso se encuentra en las obras de Peirce , Galton (Galton (1889, capítulo V)) y Lexis (Lexis (1878), Rohrbasser & Véron (2003)) c. 1875. ^{[ cita requerida ]}

[Norton-2019-1] Norton, Matthew; Khokhlov, Valentyn; Uryasev, Stan (2019). "Cálculo de CVaR y bPOE para distribuciones de probabilidad comunes con aplicación a la optimización de carteras y estimación de densidad" (PDF) . Anales de investigación de operaciones . 299 (1–2). Springer: 1281–1315. arXiv : 1811.11301 . doi :10.1007/s10479-019-03373-1. S2CID 254231768. Archivado desde el original (PDF) el 31 de marzo de 2023 . Consultado el 27 de febrero de 2023 .

[2] Distribución normal, Enciclopedia Gale de Psicología

[3] Casella y Berger (2001, pág. 102)

[4] Lyon, A. (2014). ¿Por qué las distribuciones normales son normales?, The British Journal for the Philosophy of Science.

[5] Jorge, Nocedal; Stephan, J. Wright (2006). Optimización numérica (2.ª ed.). Springer. pág. 249. ISBN 978-0387-30303-1.

[www.mathsisfun.com-6] "Distribución normal". www.mathsisfun.com . Consultado el 15 de agosto de 2020 .

[7] Stigler (1982)

[8] Halperin, Hartley y Hoel (1965, artículo 7)

[9] McPherson (1990, pág. 110)

[10] Bernardo y Smith (2000, pág. 121)

[11] Scott, Clayton; Nowak, Robert (7 de agosto de 2003). "La función Q". Connexions .

[12] Barak, Ohad (6 de abril de 2006). "Función Q y función de error" (PDF) . Universidad de Tel Aviv. Archivado desde el original (PDF) el 25 de marzo de 2009.

[13] Weisstein, Eric W. "Función de distribución normal". MathWorld .

[14] Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [junio de 1964]. "Capítulo 26, ecuación 26.2.12". Manual de funciones matemáticas con fórmulas, gráficos y tablas matemáticas . Serie de Matemáticas Aplicadas. Vol. 55 (Novena reimpresión con correcciones adicionales de la décima impresión original con correcciones (diciembre de 1972); primera ed.). Washington DC; Nueva York: Departamento de Comercio de los Estados Unidos, Oficina Nacional de Normas; Dover Publications. pág. 932. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.

[15] Vaart, AW van der (13 de octubre de 1998). Estadística asintótica. Cambridge University Press. doi :10.1017/cbo9780511802256. ISBN 978-0-511-80225-6.

[16] Portada, Thomas M.; Thomas, Joy A. (2006). Elementos de la teoría de la información . John Wiley and Sons. pág. 254. ISBN 9780471748816.

[17] Park, Sung Y.; Bera, Anil K. (2009). "Maximum Entropy Autoregressive Conditional Heteroskedasticity Model" (PDF) . Revista de Econometría . 150 (2): 219–230. CiteSeerX 10.1.1.511.9750 . doi :10.1016/j.jeconom.2008.12.014. Archivado desde el original (PDF) el 7 de marzo de 2016 . Consultado el 2 de junio de 2011 .

[Geary_RC-18] Geary RC (1936) La distribución del "cociente de Student para las muestras no normales". Suplemento del Journal of the Royal Statistical Society 3 (2): 178–184

[19] Lukacs, Eugene (marzo de 1942). "Una caracterización de la distribución normal". Anales de estadística matemática . 13 (1): 91–93. doi :10.1214/AOMS/1177731647. ISSN 0003-4851. JSTOR 2236166. MR 0006626. Zbl 0060.28509. Wikidata Q55897617.

[Patel-20] Patel y Read (1996, [2.1.4])

[21] Fan (1991, pág. 1258)

[22] Patel y Read (1996, [2.1.8])

[23] Papoulis, Athanasios. Probabilidad, variables aleatorias y procesos estocásticos (4ª ed.). pág. 148.

[24] Winkelbauer, Andreas (2012). "Momentos y momentos absolutos de la distribución normal". arXiv : 1209.4340 [math.ST].

[25] Bryc (1995, pág. 23)

[26] Bryc (1995, pág. 24)

[27] Cover y Thomas (2006, pág. 254)

[28] Williams, David (2001). Weighing the odds : a course in probability and statistics (Ed. reimpresa). Cambridge [ua]: Cambridge Univ. Press. págs. 197–199. ISBN 978-0-521-00618-7.

[29] Smith, José M. Bernardo; Adrian FM (2000). Teoría bayesiana (edición reimpresa). Chichester [ua]: Wiley. pp. 209, 366. ISBN 978-0-471-49464-5.{{cite book}}: CS1 maint: multiple names: authors list (link)

[30] O'Hagan, A. (1994) Kendall's Advanced Theory of statistics, vol. 2B, Inferencia bayesiana , Edward Arnold. ISBN 0-340-52922-9 (sección 5.40)

[Bryc_1995_35-31] Bryc (1995, pág. 35)

[32] UIUC, Clase 21. La distribución normal multivariante, 21.6: "Gaussiana individual versus gaussiana conjunta".

[33] Edward L. Melnick y Aaron Tenenbein, "Errores de especificación de la distribución normal", The American Statistician , volumen 36, número 4, noviembre de 1982, páginas 372-373

[34] "Distancia de Kullback Leibler (KL) de dos distribuciones de probabilidad normales (gaussianas)". Allisons.org . 5 de diciembre de 2007 . Consultado el 3 de marzo de 2017 .

[35] Jordan, Michael I. (8 de febrero de 2010). "Stat260: Modelado e inferencia bayesianos: la distribución conjugada previa para la distribución normal" (PDF) .

[36] Amari y Nagaoka (2000)

[37] "Esperanza del máximo de variables aleatorias gaussianas". Mathematics Stack Exchange . Consultado el 7 de abril de 2024 .

[38] "Aproximación normal a la distribución de Poisson". Stat.ucla.edu . Consultado el 3 de marzo de 2017 .

[Das-2021-39] Das, Abhranil (2021). "Un método para integrar y clasificar distribuciones normales". Journal of Vision . 21 (10): 1. arXiv : 2012.14331 . doi :10.1167/jov.21.10.1. PMC 8419883 . PMID 34468706.

[40] Bryc (1995, pág. 27)

[41] Weisstein, Eric W. "Distribución normal del producto". MathWorld . wolfram.com.

[42] Lukacs, Eugene (1942). "Una caracterización de la distribución normal". Anales de estadística matemática . 13 (1): 91–3. doi : 10.1214/aoms/1177731647 . ISSN 0003-4851. JSTOR 2236166.

[43] Basu, D.; Laha, RG (1954). "Sobre algunas caracterizaciones de la distribución normal". Sankhyā . 13 (4): 359–62. ISSN 0036-4452. JSTOR 25048183.

[44] Lehmann, EL (1997). Prueba de hipótesis estadísticas (2.ª ed.). Springer. pág. 199. ISBN 978-0-387-94919-2.

[45] Patel y Read (1996, [2.3.6])

[46] Galambos y Simonelli (2004, teorema 3.5)

[Lukacs-47] Lukacs y King (1954)

[48] Quine, MP (1993). "Sobre tres caracterizaciones de la distribución normal". Probabilidad y estadística matemática . 14 (2): 257–263.

[John-1982-49] John, S (1982). "La familia de distribuciones normales de dos piezas y tres parámetros y su ajuste". Communications in Statistics – Theory and Methods . 11 (8): 879–885. doi :10.1080/03610928208828279.

[Krishnamoorthy-50] r Krishnamoorthy (2006, pág. 127)

[51] Krishnamoorthy (2006, pág. 130)

[52] Krishnamoorthy (2006, pág. 133)

[53] Huxley (1932)

[54] Jaynes, Edwin T. (2003). Teoría de la probabilidad: la lógica de la ciencia. Cambridge University Press. pp. 592–593. ISBN 9780521592710.

[55] Oosterbaan, Roland J. (1994). "Capítulo 6: Análisis de frecuencia y regresión de datos hidrológicos" (PDF) . En Ritzema, Henk P. (ed.). Principios y aplicaciones del drenaje, publicación 16 (segunda edición revisada). Wageningen, Países Bajos: Instituto Internacional para la Recuperación y Mejora de Tierras (ILRI). pp. 175–224. ISBN 978-90-70754-33-4.

[56] Por qué la mayoría de los resultados de las investigaciones publicadas son falsos, John PA Ioannidis, 2005

[57] Wichura, Michael J. (1988). "Algoritmo AS241: Los puntos porcentuales de la distribución normal". Applied Statistics . 37 (3): 477–84. doi :10.2307/2347330. JSTOR 2347330.

[58] Johnson, Kotz y Balakrishnan (1995, Ecuación (26.48))

[59] Kinderman y Monahan (1977)

[60] Leva (1992)

[61] Marsaglia y Tsang (2000)

[62] Karney (2016)

[63] Monahan (1985, sección 2)

[64] Wallace (1996)

[66] Johnson, Kotz y Balakrishnan (1994, pág. 85)

[67] Le Cam y Lo Yang (2000, pág.74)

[69] De Moivre, Abraham (1733), Corolario I – véase Walker (1985, p. 77)

[70] Stigler (1986, pág. 76)

[72] Gauss (1809, sección 177)

[73] Gauss (1809, sección 179)

[75] Laplace (1774, Problema III)

[76] Pearson (1905, pág. 189)

[77] Gauss (1809, sección 177)

[78] Stigler (1986, pág. 144)

[79] Stigler (1978, pág. 243)

[80] Stigler (1978, pág. 244)

[81] Maxwell (1860, pág. 23)

[82] Jaynes, Edwin J.; Teoría de la probabilidad: la lógica de la ciencia , cap. 7.

[84] Peirce, Charles S. (c. 1909 MS), Collected Papers v. 6, párrafo 327.

[85] Kruskal y Stigler (1997).

[86] "Usos más tempranos... (Curva normal estándar de entrada)".

[Sun-2021-87] Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 de junio de 2021). "La distribución modificada-semi-normal: propiedades y un esquema de muestreo eficiente". Comunicaciones en Estadística – Teoría y Métodos . 52 (5): 1591–1613. doi :10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.

Función de densidad de probabilidad La curva roja es la distribución normal estándar .
Función de distribución acumulativa
Notación	${\mathcal {N}}(\mu,\sigma ^{2})$
Parámetros	$\mu \in \mathbb {R}$ = media ( ubicación ) = varianza ( escala al cuadrado ) $\sigma ^{2}\in \mathbb {R} _{>0}$
Apoyo	$x\in \mathbb {R}$
PDF	${\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}$
CDF	$\Phi \left({\frac {x-\mu }{\sigma }}\right)={\frac {1}{2}}\left[1+\operatorname {erf} \left({\frac {x-\mu }{\sigma {\sqrt {2}}}}\right)\right]$
Cuantil	$\mu +\sigma {\sqrt {2}}\operatorname {erf} ^{-1}(2p-1)$
Significar	${\estilo de visualización \mu}$
Mediana	${\estilo de visualización \mu}$
Modo	${\estilo de visualización \mu}$
Diferencia	$\sigma ^{2}$
ENOJADO	$\sigma {\sqrt {2/\pi }}$
Oblicuidad	${\estilo de visualización 0}$
Exceso de curtosis	${\estilo de visualización 0}$
Entropía	${\frac {1}{2}}\log(2\pi e\sigma ^{2})$
MGF	$\exp(\mu t+\sigma ^{2}t^{2}/2)$
CF	$\exp(i\mu t-\sigma ^{2}t^{2}/2)$
Información de Fisher	${\mathcal {I}}(\mu ,\sigma )={\begin{pmatrix}1/\sigma ^{2}&0\\0&2/\sigma ^{2}\end{pmatrix}}$ ${\mathcal {I}}(\mu ,\sigma ^{2})={\begin{pmatrix}1/\sigma ^{2}&0\\0&1/(2\sigma ^{4})\end{pmatrix}}$
Divergencia de Kullback-Leibler	${1 \over 2}\left\{\left({\frac {\sigma _{0}}{\sigma _{1}}}\right)^{2}+{\frac {(\mu _{1}-\mu _{0})^{2}}{\sigma _{1}^{2}}}-1+\ln {\sigma _{1}^{2} \over \sigma _{0}^{2}}\right\}$
Déficit esperado	$\mu -\sigma {\frac {{\frac {1}{\sqrt {2\pi }}}e^{\frac {-\left(q_{p}\left({\frac {X-\mu }{\sigma }}\right)\right)^{2}}{2}}}{1-p}}$ ^[1]