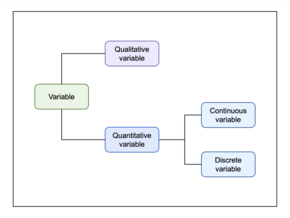
Variable continua o discreta

Parte de una serie sobre estadísticas
Teoría de la probabilidad
Probabilidad Axiomas Determinismo Sistema Indeterminismo Aleatoriedad
Espacio de probabilidad Espacio muestral Evento Eventos colectivamente exhaustivos Evento elemental Exclusividad mutua Resultado Semifallo Experimento El proceso de Bernoulli Distribución de probabilidad Distribución de Bernoulli Binomial distribution Exponential distribution Normal distribution Pareto distribution Poisson distribution Probability measure Random variable Bernoulli process Continuous or discrete Expected value Variance Markov chain Observed value Random walk Stochastic process
Complementary event Joint probability Marginal probability Conditional probability
Independence Conditional independence Law of total probability Law of large numbers Bayes' theorem Boole's inequality
Venn diagram Tree diagram
v t e

En matemáticas y estadística , una variable cuantitativa puede ser continua o discreta si se obtienen típicamente midiendo o contando , respectivamente. ^[1] Si puede tomar dos valores reales particulares de modo que también pueda tomar todos los valores reales entre ellos (incluidos los valores que están arbitrariamente o infinitesimalmente cerca uno del otro), la variable es continua en ese intervalo . ^[2] Si puede tomar un valor tal que hay un espacio no infinitesimal a cada lado que no contiene valores que la variable pueda tomar, entonces es discreta alrededor de ese valor. ^[3] En algunos contextos, una variable puede ser discreta en algunos rangos de la línea numérica y continua en otros.

Una variable continua es una variable tal que existen valores posibles entre dos valores cualesquiera.

Por ejemplo, una variable en un rango no vacío de números reales es continua si puede tomar cualquier valor en ese rango. ^[4]

Los métodos de cálculo se utilizan a menudo en problemas en los que las variables son continuas, por ejemplo en problemas de optimización continua. ^[5]

En teoría estadística , las distribuciones de probabilidad de variables continuas se pueden expresar en términos de funciones de densidad de probabilidad . ^[6]

En la dinámica de tiempo continuo , la variable tiempo se trata como continua, y la ecuación que describe la evolución de alguna variable a lo largo del tiempo es una ecuación diferencial . ^[7] La ​​tasa instantánea de cambio es un concepto bien definido que toma la relación del cambio en la variable dependiente a la variable independiente en un instante específico.

Por el contrario, una variable es una variable discreta si y solo si existe una correspondencia biunívoca entre esta variable y un subconjunto de , el conjunto de números naturales . ^[8] En otras palabras, una variable discreta en un intervalo particular de valores reales es aquella para la cual, para cualquier valor en el rango que se le permite tomar a la variable, existe una distancia mínima positiva al otro valor permisible más cercano. El valor de una variable discreta se puede obtener contando, y el número de valores permitidos es finito o infinito contable . Ejemplos comunes son las variables que deben ser números enteros , números enteros no negativos, números enteros positivos o solo los números enteros 0 y 1. ^[9]${\displaystyle \mathbb {N} }$

Los métodos de cálculo no se prestan fácilmente a problemas que involucran variables discretas. Especialmente en el cálculo multivariable, muchos modelos se basan en el supuesto de continuidad. ^[10] Algunos ejemplos de problemas que involucran variables discretas incluyen la programación entera .

En estadística, las distribuciones de probabilidad de variables discretas se pueden expresar en términos de funciones de masa de probabilidad . ^[6]

En la dinámica de tiempo discreto , la variable tiempo se trata como discreta y la ecuación de evolución de alguna variable a lo largo del tiempo se denomina ecuación diferencial . ^[11] Para ciertos sistemas dinámicos de tiempo discreto, la respuesta del sistema se puede modelar resolviendo la ecuación diferencial para obtener una solución analítica.

En econometría y, de manera más general, en el análisis de regresión , a veces algunas de las variables que se relacionan empíricamente entre sí son variables 0-1, y se les permite tomar solo esos dos valores. ^[12] El propósito de los valores discretos de 0 y 1 es utilizar la variable ficticia como un "interruptor" que puede "encenderse" y "apagarse" asignando los dos valores a diferentes parámetros en una ecuación. Una variable de este tipo se llama variable ficticia . Si la variable dependiente es una variable ficticia, entonces se emplea comúnmente la regresión logística o la regresión probit . En el caso del análisis de regresión, una variable ficticia se puede utilizar para representar subgrupos de la muestra en un estudio (por ejemplo, el valor 0 corresponde a un constituyente del grupo de control). ^[13]

Un modelo multivariado mixto puede contener variables tanto discretas como continuas. Por ejemplo, un modelo multivariado mixto simple podría tener una variable discreta , que solo toma valores 0 o 1, y una variable continua . ^[14] Un ejemplo de un modelo mixto podría ser un estudio de investigación sobre el riesgo de trastornos psicológicos basado en una medida binaria de síntomas psiquiátricos y una medida continua de rendimiento cognitivo. ^[15] Los modelos mixtos también pueden involucrar una sola variable que sea discreta en algún rango de la línea numérica y continua en otro rango.${\displaystyle x}$${\displaystyle y}$

En teoría de probabilidad y estadística, la distribución de probabilidad de una variable aleatoria mixta consta de componentes discretos y continuos. Una variable aleatoria mixta no tiene una función de distribución acumulativa que sea discreta o continua en todas partes. Un ejemplo de una variable aleatoria de tipo mixto es la probabilidad de tiempo de espera en una cola. La probabilidad de que un cliente experimente un tiempo de espera cero es discreta, mientras que los tiempos de espera distintos de cero se evalúan en una escala de tiempo continua. ^[16] En física (particularmente en mecánica cuántica, donde este tipo de distribución surge a menudo), las funciones delta de Dirac se utilizan a menudo para tratar componentes continuos y discretos de manera unificada. Por ejemplo, el ejemplo anterior podría describirse mediante una densidad de probabilidad , tal que , y .${\displaystyle p(t)=\alpha \delta (t)+g(t)}$${\displaystyle P(t>0)=\int _{0}^{\infty }g(t)=1-\alpha }$${\displaystyle P(t=0)=\alpha }$