Red Zobel

Para el filtro de onda inventado por Zobel y que a veces lleva su nombre, consulte filtros derivados de m .

Las redes Zobel son un tipo de sección de filtro basada en el principio de diseño de impedancia de imagen . Reciben su nombre de Otto Zobel de Bell Labs , quien publicó un artículo muy citado sobre filtros de imagen en 1923. ^[1] La característica distintiva de las redes Zobel es que la impedancia de entrada se fija en el diseño independientemente de la función de transferencia . Esta característica se logra a expensas de un recuento de componentes mucho mayor en comparación con otros tipos de secciones de filtro. La impedancia normalmente se especificaría como constante y puramente resistiva . Por esta razón, las redes Zobel también se conocen como redes de resistencia constante . Sin embargo, es posible cualquier impedancia alcanzable con componentes discretos.

Las redes Zobel se utilizaban mucho en el pasado en telecomunicaciones para aplanar y ampliar la respuesta de frecuencia de las líneas terrestres de cobre, produciendo una línea de mayor rendimiento que una originalmente destinada al uso telefónico común. La tecnología analógica ha dado paso a la tecnología digital y ahora se utilizan poco.

Cuando se utiliza para cancelar la parte reactiva de la impedancia del altavoz , el diseño a veces se denomina celda de Boucherot . En este caso, solo la mitad de la red se implementa como componentes fijos, y la otra mitad son los componentes reales e imaginarios de la impedancia del altavoz . Esta red es más parecida a los circuitos de corrección del factor de potencia utilizados en la distribución de energía eléctrica, de ahí la asociación con el nombre de Boucherot.

Una forma común de circuito de redes Zobel es una red en T con puente . Este término se usa a menudo para referirse a una red Zobel, a veces incorrectamente cuando la implementación del circuito no es una T con puente.

Partes de este artículo o sección se basan en el conocimiento del lector de la representación de impedancia compleja de capacitores e inductores y del conocimiento de la representación de señales en el dominio de frecuencia .

La base de una red Zobel es un circuito puente equilibrado, como se muestra en el circuito de la derecha. La condición para el equilibrio es que:

${\displaystyle {\frac {Z}{Z_{0}}}={\frac {Z_{0}}{Z'}}}$

Si esto se expresa en términos de un Z ₀  = 1 normalizado como se hace convencionalmente en las tablas de filtros, entonces la condición de equilibrio es simplemente;

${\displaystyle Z={\frac {1}{Z'}}}$

O bien, es simplemente la impedancia inversa o dual de .${\displaystyle \scriptstyle Z'}$${\displaystyle \scriptstyle Z}$

La impedancia de puente Z _B se encuentra entre los puntos de equilibrio y, por lo tanto, no tiene potencial a través de ellos. En consecuencia, no consumirá corriente y su valor no afecta al funcionamiento del circuito. Su valor suele elegirse como Z ₀ por razones que se aclararán en el análisis de los circuitos T puenteados que se realizará más adelante.

La impedancia de entrada está dada por

${\displaystyle {\frac {1}{Z_{\text{in}}}}={\frac {1}{Z_{0}+Z'}}+{\frac {1}{Z+Z_{0) }}}}$

Sustituyendo la condición de equilibrio,

${\displaystyle Z'={\frac {Z_{0}^{2}}{Z}}}$

rendimientos

${\displaystyle Z_{\text{in}}=Z_{0}}$

La impedancia de entrada se puede diseñar para que sea puramente resistiva estableciendo

${\displaystyle Z_{0}=R_{0}\!\,}$

La impedancia de entrada será entonces real e independiente de ω en banda y fuera de banda sin importar la complejidad de la sección de filtro elegida.

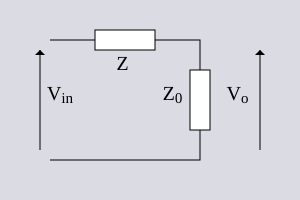
Si se toma la Z ₀ en la parte inferior derecha del puente como la carga de salida, entonces se puede calcular una función de transferencia de V _o / V _in para la sección. Solo se debe considerar la rama RHS (lado derecho) en este cálculo. La razón de esto se puede ver considerando que no hay flujo de corriente a través de Z _B . Ninguna de la corriente que fluye a través de la rama LHS (lado izquierdo) fluirá hacia la carga. La rama LHS, por lo tanto, no puede afectar la salida. Ciertamente afecta la impedancia de entrada (y, por lo tanto, el voltaje del terminal de entrada), pero no la función de transferencia. Ahora se puede ver fácilmente que la función de transferencia es;

${\displaystyle A(\omega )={\frac {Z_{0}}{Z+Z_{0}}}}$

La impedancia de carga es en realidad la impedancia de la siguiente etapa o de una línea de transmisión y se puede omitir del diagrama del circuito. Si también establecemos:

${\displaystyle Z_{B}=Z_{0}\,\!}$

Entonces se obtiene el circuito de la derecha. Esto se conoce como circuito T puenteado porque se ve que la impedancia Z "hace puente" a través de la sección T. El propósito de establecer Z _B  =  Z ₀ es hacer que la sección del filtro sea simétrica. Esto tiene la ventaja de que presentará la misma impedancia, Z ₀ , tanto en el puerto de entrada como en el de salida.

Se puede implementar una sección de filtro Zobel para paso bajo, paso alto, paso banda o eliminación de banda. También es posible implementar un atenuador de respuesta de frecuencia plana. Esto último es de cierta importancia para las secciones de filtro prácticas que se describen más adelante.

Para una sección atenuadora, Z es simplemente

${\displaystyle Z=R\,\!}$

y,

${\displaystyle Z'=R'={\frac {R_{0}^{2}}{R}}}$

La atenuación de la sección viene dada por;

${\displaystyle L=20\log \left({\frac {R}{R_{0}}}+1\right)\,{\text{dB}}}$

Para una sección de filtro de paso bajo, Z es un inductor y Z  ' es un condensador;

${\displaystyle Z=i\omega L\!\,}$

y

${\displaystyle Z'={\frac {1}{i\omega C'}}}$

dónde

${\displaystyle C'={\frac {L}{R_{0}^{2}}}}$

La función de transferencia de la sección está dada por

${\displaystyle A(\omega )={\frac {R_{0}}{i\omega L+R_{0}}}}$

El punto de 3 dB ocurre cuando ωL = R _0, por lo que la frecuencia de corte de 3 dB viene dada por

${\displaystyle \omega _ {c}={\frac {R_ {0}}{L}}}$

donde ω está en la banda de detención muy por encima de ω _c ,

${\displaystyle A(\omega )\approx {\frac {R_{0}}{i\omega L}}}$

De esto se puede ver que A ( ω ) está cayendo en la banda de parada en los clásicos 6 dB/ 8ve (o 20 dB/década).

Para una sección de filtro de paso alto, Z es un capacitor y Z' es un inductor:

${\displaystyle Z={\frac {1}{i\omega C}}}$

y

${\displaystyle Z'=i\omega L'\!\,}$

dónde

${\displaystyle L'=CR_{0}^{2}\!\,}$

La función de transferencia de la sección está dada por

${\displaystyle A(\omega )={\frac {i\omega CR_{0}}{1+i\omega CR_{0}}}}$

El punto de 3 dB ocurre cuando ωC  =  1 ⁄ R _0, por lo que la frecuencia de corte de 3 dB viene dada por

${\displaystyle \omega _{c}={\frac {1}{CR_{0}}}}$

En la banda de parada,

${\displaystyle A(\omega )\approx i\omega CR_{0}}$

cayendo a 6 dB/8ve con frecuencia decreciente.

Para una sección de filtro de paso de banda, Z es un circuito resonante en serie y Z' es un circuito resonante en derivación;

${\displaystyle Z=i\omega L+{\frac {1}{i\omega C}}}$

y

${\displaystyle Y'={\frac {1}{Z'}}=i\omega C'+{\frac {1}{i\omega L'}}}$

La función de transferencia de la sección está dada por

${\displaystyle A(\omega )={\frac {i\omega CR_{0}}{1+i\omega CR_{0}-\omega ^{2}LC}}}$

El punto de 3 dB ocurre cuando |1 −  ω ² LC | =  ωCR _0, por lo que las frecuencias de corte de 3 dB están dadas por

${\displaystyle \omega _{c}={\frac {1}{2LC}}\left(\pm R_{0}C+{\sqrt {R_{0}^{2}C^{2}+4LC}}\right)}$

a partir de la cual se pueden determinar la frecuencia central, ω _m , y el ancho de banda, Δ ω :

${\displaystyle {\begin{aligned}\Delta \omega &={\frac {R_{0}}{L}}\\\omega _{m}&={\sqrt {{\frac {R_{0}^{2}}{4L^{2}}}+{\frac {1}{LC}}}}\end{aligned}}}$

Tenga en cuenta que esto es diferente de la frecuencia de resonancia.

${\displaystyle \omega _{0}={\sqrt {\frac {1}{LC}}}}$

La relación entre ellos se da por

${\displaystyle \omega _{m}^{2}=\left({\frac {\Delta \omega }{2}}\right)^{2}+\omega _{0}^{2}}$

Para una sección de filtro de banda eliminada, Z es un circuito resonante en derivación y Z' es un circuito resonante en serie:

${\displaystyle Y={\frac {1}{Z}}=i\omega C+{\frac {1}{i\omega L}}}$

y

${\displaystyle Z'=i\omega L'+{\frac {1}{i\omega C'}}}$

La función de transferencia y el ancho de banda se pueden encontrar por analogía con la sección de paso de banda.

${\displaystyle \Delta \omega ={\frac {1}{CR_{0}}}}$

Y,

${\displaystyle \omega _{m}={\sqrt {\left({\frac {1}{2R_{0}C}}\right)^{2}+{\frac {1}{LC}}}}}$

Las redes Zobel rara vez se utilizan para el filtrado de frecuencia tradicional. Otros tipos de filtros son significativamente más eficientes para este propósito. Donde los Zobel se destacan es en aplicaciones de ecualización de frecuencia, particularmente en líneas de transmisión. La dificultad con las líneas de transmisión es que la impedancia de la línea varía de manera compleja a lo largo de la banda y es tediosa de medir. Para la mayoría de los tipos de filtros, esta variación en la impedancia causará una diferencia significativa en la respuesta a la teórica y es matemáticamente difícil de compensar, incluso suponiendo que la impedancia se conoce con precisión. Sin embargo, si se utilizan redes Zobel, solo es necesario medir la respuesta de la línea en una carga resistiva fija y luego diseñar un ecualizador para compensarla. Es completamente innecesario saber nada sobre la impedancia de la línea, ya que la red Zobel presentará exactamente la misma impedancia a la línea que los instrumentos de medición. Por lo tanto, su respuesta será exactamente como se predijo teóricamente. Esta es una gran ventaja cuando se desean líneas de alta calidad con respuestas de frecuencia planas.

En el caso de las líneas de audio, siempre es necesario combinar componentes de filtro L/C con componentes atenuadores resistivos en la misma sección de filtro. La razón de ello es que la estrategia de diseño habitual consiste en exigir que la sección atenúe todas las frecuencias hasta el nivel de la frecuencia de la banda de paso con el nivel más bajo. Sin los componentes resistivos, el filtro, al menos en teoría, aumentaría la atenuación sin límite. La atenuación en la banda de rechazo del filtro (es decir, la atenuación máxima limitante) se denomina "pérdida básica" de la sección. En otras palabras, la parte plana de la banda se atenúa mediante la pérdida básica hasta el nivel de la parte descendente de la banda que se desea ecualizar. La siguiente discusión de secciones prácticas se relaciona en particular con las líneas de transmisión de audio.

El efecto más significativo que se debe compensar es que, en una determinada frecuencia de corte, la respuesta de la línea comienza a disminuir como un simple filtro de paso bajo. El ancho de banda efectivo de la línea se puede aumentar con una sección que sea un filtro de paso alto que coincida con esta disminución, combinado con un atenuador. En la parte plana de la banda de paso, solo es significativa la parte del atenuador de la sección del filtro. Esta se establece en una atenuación igual al nivel de la frecuencia más alta de interés. Todas las frecuencias hasta este punto se ecualizarán de manera plana a un nivel atenuado. Por encima de este punto, la salida del filtro comenzará a disminuir nuevamente.

En las redes de telecomunicaciones, es bastante común que un circuito esté formado por dos secciones de línea que no tienen la misma impedancia característica . Por ejemplo, 150 Ω y 300 Ω. Un efecto de esto es que la reducción puede comenzar en 6 dB/octava en una frecuencia de corte inicial , pero luego puede volverse repentinamente más pronunciada. Esta situación requiere (al menos) dos secciones de paso alto para compensar cada una operando a una frecuencia diferente .${\displaystyle \scriptstyle f_{c1}}$${\displaystyle \scriptstyle f_{c2}}$${\displaystyle \scriptstyle f_{c}}$

Las protuberancias y las depresiones en la banda de paso se pueden compensar con secciones de paso de banda y de supresión de banda respectivamente. También se requiere un elemento atenuador, pero normalmente bastante más pequeño que el necesario para la reducción gradual. Estas anomalías en la banda de paso pueden ser causadas por segmentos de línea no coincidentes, como se describió anteriormente. Las depresiones también pueden ser causadas por variaciones de temperatura del suelo.

Ocasionalmente, se incluye una sección de paso bajo para compensar la caída excesiva del transformador de línea en el extremo de baja frecuencia. Sin embargo, este efecto suele ser muy pequeño en comparación con los otros efectos mencionados anteriormente.

Las secciones de baja frecuencia suelen tener inductores de valores altos. Dichos inductores tienen muchas vueltas y, en consecuencia, tienden a tener una resistencia significativa. Para mantener la resistencia constante de la sección en la entrada, la rama dual del puente T debe contener un dual de la resistencia parásita, es decir, una resistencia en paralelo con el condensador. Incluso con la compensación, la resistencia parásita sigue teniendo el efecto de insertar atenuación en las frecuencias bajas. Esto, a su vez, tiene el efecto de reducir ligeramente la cantidad de elevación de baja frecuencia que la sección habría producido de otro modo. La pérdida básica de la sección se puede aumentar en la misma cantidad que la resistencia parásita que se inserta y esto devolverá la elevación de baja frecuencia lograda al valor para el que se diseñó.

La compensación de la resistencia del inductor no es un problema en frecuencias altas, donde los inductores tienden a ser más pequeños. En cualquier caso, para una sección de paso alto, el inductor está en serie con la resistencia de pérdida básica y la resistencia parásita simplemente se puede restar de esa resistencia. Por otro lado, la técnica de compensación puede ser necesaria para secciones resonantes, especialmente un resonador de Q alto que se utiliza para levantar una banda muy estrecha. Para estas secciones, el valor de los inductores también puede ser grande.

Se puede utilizar un filtro de paso alto de atenuación ajustable para compensar los cambios en la temperatura del suelo. La temperatura del suelo varía muy lentamente en comparación con la temperatura de la superficie. Por lo general, solo se requieren ajustes entre 2 y 4 veces al año para aplicaciones de audio.

Un filtro completo típico constará de una serie de secciones Zobel para la reducción gradual, las caídas de frecuencia y la temperatura, seguidas de una sección de atenuador plano para reducir el nivel a una atenuación estándar. A esto le sigue un amplificador de ganancia fija para volver a llevar la señal a un nivel utilizable, normalmente 0 dBu . La ganancia del amplificador suele ser de 45 dB como máximo . Si es más, la amplificación del ruido de línea tenderá a cancelar los beneficios de calidad del ancho de banda mejorado. Este límite de amplificación limita esencialmente cuánto se puede aumentar el ancho de banda con estas técnicas. Ninguna parte de la banda de señal entrante se amplificará por los 45 dB completos . Los 45 dB se componen de la pérdida de línea en la parte plana de su espectro más la pérdida básica de cada sección. En general, cada sección tendrá una pérdida mínima en una banda de frecuencia diferente, por lo tanto, la amplificación en esa banda se limitará a la pérdida básica de solo esa sección del filtro, asumiendo una superposición insignificante. Una opción típica para R ₀ es 600 Ω. Un transformador de buena calidad (generalmente esencial, pero no se muestra en el diagrama), conocido como bobina repetidora , se encuentra al comienzo de la cadena donde termina la línea.

Además de la T puenteada, hay otras posibles formas de sección que se pueden utilizar.

Como se mencionó anteriormente, se puede configurar en cualquier impedancia deseada sin afectar la impedancia de entrada. En particular, si se configura como un circuito abierto o un cortocircuito, se obtiene un circuito de sección simplificado, llamado secciones en L. Estas se muestran arriba para el caso de una sección de paso alto con pérdida básica.${\displaystyle \scriptstyle Z_{B}}$

El puerto de entrada aún presenta una impedancia de (siempre que la salida esté terminada en ) pero el puerto de salida ya no presenta una impedancia constante. Tanto las secciones L de circuito abierto como las de cortocircuito se pueden invertir de modo que se presente en la salida y la impedancia variable en la entrada.${\displaystyle \scriptstyle R_{0}}$${\displaystyle \scriptstyle R_{0}}$${\displaystyle \scriptstyle R_{0}}$

Para conservar el beneficio de la impedancia constante de las redes Zobel, el puerto de impedancia variable no debe estar orientado hacia la impedancia de línea. Tampoco debe estar orientado hacia el puerto de impedancia variable de otra sección en L. El hecho de que esté orientado hacia el amplificador es aceptable, ya que la impedancia de entrada del amplificador normalmente está configurada para estar dentro de tolerancias aceptables. En otras palabras, la impedancia variable no debe estar orientada hacia la impedancia variable.${\displaystyle \scriptstyle R_{0}}$

Las redes Zobel descritas aquí se pueden utilizar para igualar líneas terrestres compuestas por cables de par trenzado o de cuadrete en estrella . La naturaleza de circuito equilibrado de estas líneas proporciona una buena relación de rechazo en modo común (CMRR). Para mantener la CMRR, los circuitos conectados a la línea deben mantener el equilibrio. Por este motivo, a veces se requieren versiones equilibradas de las redes Zobel. Esto se logra reduciendo a la mitad la impedancia de los componentes en serie y luego colocando componentes idénticos en el tramo de retorno del circuito.

La sección AC es una versión balanceada de una sección L. El equilibrio se logra de la misma manera que en una sección T con puente completo balanceado, colocando la mitad de la impedancia en serie en lo que era el conductor común. Las secciones C, al igual que la sección L de la que se derivan, pueden presentarse en variedades de circuito abierto y de cortocircuito. Las mismas restricciones se aplican a las secciones C con respecto a las terminaciones de impedancia que a las secciones L.

Es posible transformar una sección en T puenteada en una sección reticular o en X (véase el teorema de bisección de Bartlett ). ^[2] La sección en X es un tipo de circuito puente, pero normalmente se dibuja como una red, de ahí el nombre. Su topología la hace intrínsecamente equilibrada, pero nunca se utiliza para implementar los filtros de resistencia constante del tipo descrito aquí debido al aumento del número de componentes. El aumento del número de componentes surge del proceso de transformación en lugar del equilibrio. Sin embargo, hay una aplicación común para esta topología, el ecualizador de fase reticular , que también es de resistencia constante y también inventado por Zobel. Este circuito se diferencia de los descritos aquí en que el circuito puente no está generalmente en condición equilibrada.

En lo que respecta a los filtros de resistencia constante, el término media sección tiene un significado algo diferente al de otros tipos de filtros de imagen. Generalmente, una media sección se forma cortando el punto medio de la impedancia en serie y la admitancia en derivación de una sección completa de una red en escalera . Es literalmente media sección. Aquí, sin embargo, hay una definición algo diferente. Una media sección es la impedancia en serie (semisección en serie) o la admitancia en derivación (semisección en derivación) que, cuando se conecta entre las impedancias de fuente y carga de R ₀ , dará como resultado la misma función de transferencia que algún circuito de resistencia constante arbitrario. El propósito de usar medias secciones es que se logra la misma funcionalidad con un recuento de componentes drásticamente reducido.

Si un circuito de resistencia constante tiene una entrada V _in , entonces un generador con una impedancia R ₀ debe tener un voltaje de circuito abierto de E=2V _in para producir V _in en la entrada del circuito de resistencia constante. Si ahora el circuito de resistencia constante se reemplaza por una impedancia de 2Z, como en el diagrama anterior, se puede ver por simple simetría que el voltaje V _in aparecerá en la mitad de la impedancia 2Z. La salida de este circuito ahora se puede calcular como,

${\displaystyle {\frac {V_{O}}{V_{in}}}={\frac {R_{0}}{Z+R_{0}}}}$

que es exactamente lo mismo que una sección en T puenteada con un elemento en serie Z. La semisección en serie es, por lo tanto, una impedancia en serie de 2Z. Por el razonamiento correspondiente, la semisección en derivación es una impedancia en derivación de 1 ⁄ 2 Z' (o el doble de la admitancia).

Es importante destacar que estas medias secciones están lejos de ser de resistencia constante. Tienen la misma función de transferencia que una red de resistencia constante, pero solo cuando están correctamente terminadas. Un ecualizador no dará buenos resultados si una media sección se coloca frente a la línea, ya que la línea tendrá una impedancia variable (y probablemente desconocida). Asimismo, dos medias secciones no se pueden conectar directamente entre sí, ya que ambas tendrán impedancias variables. Sin embargo, si se coloca un atenuador suficientemente grande entre las dos impedancias variables, esto tendrá el efecto de enmascarar el efecto. Un atenuador de alto valor tendrá una impedancia de entrada sin importar cuál sea la impedancia de terminación en el otro lado. En la cadena práctica de ejemplo que se muestra arriba, se requiere un atenuador de 22 dB en la cadena. No es necesario que esté al final de la cadena, se puede colocar en cualquier lugar deseado y se puede usar para enmascarar dos impedancias desparejadas. También se puede dividir en dos o más partes y usar para enmascarar más de una despareja.${\displaystyle \scriptstyle \approx R_{0}}$

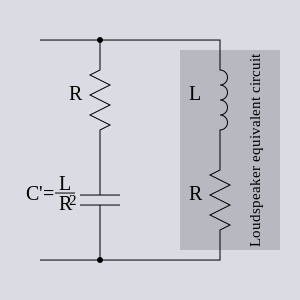
Véase también célula de Boucherot

Las redes Zobel se pueden utilizar para hacer que la impedancia que presenta un altavoz a la salida de su amplificador aparezca como una resistencia constante. Esto es beneficioso para el rendimiento del amplificador. La impedancia de un altavoz es en parte resistiva. La resistencia representa la energía transferida desde el amplificador a la salida de sonido más algunas pérdidas de calor en el altavoz. Sin embargo, el altavoz también posee inductancia debido a los devanados de su bobina. La impedancia del altavoz se modela típicamente como una resistencia y un inductor en serie. Un circuito paralelo de una resistencia y un condensador en serie de los valores correctos formará un puente Zobel. Es obligatorio elegir porque el punto central entre el inductor y la resistencia es inaccesible (y, de hecho, ficticio: la resistencia y el inductor son cantidades distribuidas como en una línea de transmisión ). El altavoz se puede modelar con mayor precisión mediante un circuito equivalente más complejo. La red Zobel compensadora también se volverá más compleja en el mismo grado. ^[3]${\displaystyle \scriptstyle R_{B}\;=\;\infty }$

Tenga en cuenta que el circuito funcionará igual de bien si se intercambian el condensador y la resistencia. En este caso, el circuito ya no es un puente balanceado de Zobel, pero claramente la impedancia no ha cambiado. Se podría haber llegado al mismo circuito diseñando desde el punto de vista de la minimización de la potencia reactiva de Boucherot . Desde este enfoque de diseño, no hay diferencia en el orden del condensador y la resistencia y la celda de Boucherot podrían considerarse una descripción más precisa.

Las redes Zobel se pueden utilizar para la ecualización de líneas de vídeo y de audio. Sin embargo, se adopta un enfoque notablemente diferente con los dos tipos de señales. La diferencia en las características del cable se puede resumir de la siguiente manera:

• El video comúnmente utiliza cable coaxial que requiere una topología no balanceada para los filtros, mientras que el audio comúnmente utiliza par trenzado que requiere una topología balanceada.
• El video requiere un ancho de banda más amplio y una especificación de fase diferencial más estricta , lo que a su vez resulta en una especificación dimensional más estricta para el cable.
• Las especificaciones más estrictas para los cables de vídeo tienden a producir una impedancia característica sustancialmente constante en una banda ancha (normalmente nominalmente 75 Ω). Por otro lado, el cable de audio puede tener nominalmente 600 Ω (300 Ω y 150 Ω también son valores estándar), pero en realidad solo medirá este valor a 800 Hz. A frecuencias más bajas será mucho más alta y a frecuencias más altas será más baja y más reactiva.

• Estas características dan como resultado una respuesta más suave y con mejor comportamiento para las líneas de video sin ninguna de las desagradables discontinuidades que se encuentran típicamente en las líneas de audio. Estas discontinuidades en la respuesta de frecuencia a menudo son causadas por el hábito de las compañías de telecomunicaciones de formar una conexión uniendo dos líneas más cortas de diferente impedancia característica. Las líneas de video, por otro lado, tienden a disminuir suavemente con la frecuencia de una manera predecible.

Esta respuesta más predecible del vídeo permite un enfoque de diseño diferente. El ecualizador de vídeo está construido como una única sección en T con puente pero con una red bastante más compleja para Z. Para líneas cortas, o para un ecualizador de recorte, se puede utilizar una topología de filtro de Bode. Para líneas más largas, se puede utilizar una red con topología de filtro de Cauer . Otro factor que impulsa este enfoque es el hecho de que una señal de vídeo ocupa una gran cantidad de octavas, alrededor de 20 o más. Si se ecualiza con secciones básicas simples, se necesitaría una gran cantidad de secciones de filtro. Las secciones simples están diseñadas, por lo general, para ecualizar un rango de una o dos octavas.

Una red de Bode, al igual que una red Zobel, es una red de puente simétrico T que cumple la condición de k constante . Sin embargo, no cumple la condición de resistencia constante, es decir, el puente no está en equilibrio. ^[4] Cualquier red de impedancia, Z, se puede utilizar en una red de Bode, al igual que con una red Zobel, pero la sección de paso alto que se muestra para corregir frecuencias de gama alta es la más común. Una red de Bode terminada en una resistencia variable se puede utilizar para producir una impedancia variable en los terminales de entrada de la red. Una propiedad útil de esta red es que la impedancia de entrada se puede hacer variar de una impedancia capacitiva a través de una impedancia puramente resistiva a una impedancia inductiva, todo ello ajustando el potenciómetro de carga única , R _L . La resistencia de puente, R ₀ , se elige para que sea igual a la impedancia nominal de modo que en el caso especial cuando R _L se establece en R ₀ la red se comporta como una red Zobel y Z _in también es igual a R ₀ .

La red de Bode se utiliza en un ecualizador conectando toda la red de forma que la impedancia de entrada de la red de Bode, Z _en , esté en serie con la carga. Dado que la impedancia de la red de Bode puede ser capacitiva o inductiva según la posición del potenciómetro de ajuste, la respuesta puede ser un aumento o un corte de la banda de frecuencias sobre la que actúa. La función de transferencia de esta disposición es:

${\displaystyle A(\omega )={\frac {R_{0}}{Z_{in}+R_{0}}}}$

El ecualizador de Bode se puede convertir en un filtro de resistencia constante utilizando toda la red de Bode como la rama Z de una red de Zobel, lo que da como resultado una red bastante compleja de redes de puente T integradas en un puente T más grande. Se puede ver que esto da como resultado la misma función de transferencia al notar que la función de transferencia del ecualizador de Bode es idéntica a la función de transferencia de la forma general del ecualizador de Zobel. Tenga en cuenta que el dual de una red de puente T de resistencia constante es la red idéntica. El dual de una red de Bode es, por lo tanto, la misma red excepto por la resistencia de carga R _L , que debe ser la inversa, R _L ', en el circuito dual. Para ajustar el ecualizador, R _L y R _L ' deben estar agrupados, o de lo contrario mantenerse en paso de tal manera que a medida que R _L aumenta, R _L ' disminuirá y viceversa.

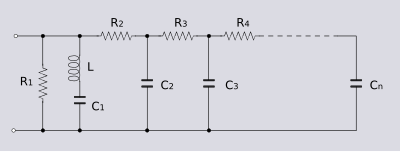
Para ecualizar líneas de vídeo largas, se utiliza una red con topología Cauer como impedancia Z de una red de resistencia constante Zobel. Del mismo modo que la impedancia de entrada de una red Bode se utiliza como impedancia Z de una red Zobel para formar un ecualizador Zobel Bode, la impedancia de entrada de una red Cauer se utiliza para formar un ecualizador Zobel Cauer. El ecualizador es necesario para corregir una atenuación que aumenta con la frecuencia y para ello se requiere una red Cauer en escalera formada por resistencias en serie y condensadores en derivación. Opcionalmente, puede haber un inductor incluido en serie con el primer condensador que aumenta la ecualización en el extremo superior debido a la pendiente más pronunciada que se produce a medida que se aproxima a la resonancia. Esto puede ser necesario en líneas más largas. La resistencia en derivación R ₁ proporciona la pérdida básica de la red Zobel de la forma habitual.

El dual de una red RC Cauer es una red LR Cauer que se requiere para la impedancia Z' como se muestra en el ejemplo. El ajuste es un poco problemático con este ecualizador. Para mantener la resistencia constante, los pares de componentes C ₁ / L ₁ ', C ₂ / L ₂ ', etc., deben permanecer con impedancias duales a medida que se ajusta el componente, por lo que ambas partes del par deben ajustarse juntas. Con el ecualizador Zobel Bode, esto es una simple cuestión de juntar dos potenciómetros: una configuración de componentes disponible en el mercado. Sin embargo, juntar un capacitor variable y un inductor no es una solución muy práctica. Estos ecualizadores tienden a ser "construidos a mano", una solución es seleccionar los capacitores en la prueba y ajustar valores fijos de acuerdo con las mediciones y luego ajustar los inductores hasta que se logre la coincidencia requerida. El elemento más alejado de la escalera desde el punto de excitación es ecualizar la frecuencia más baja de interés. Esto se ajusta primero, ya que también tendrá un efecto en las frecuencias más altas y desde allí se ajustan progresivamente las frecuencias más altas trabajando a lo largo de la escalera hacia el punto de conducción.

Wikimedia Commons alberga una categoría multimedia sobre Redes Zobel .

• Topología de filtro electrónico
• Impedancia de la imagen
• Filtros k constantes
• filtros derivados de m
• Célula de Boucherot