Filtro Butterworth

El filtro Butterworth es un tipo de filtro de procesamiento de señales diseñado para tener una respuesta de frecuencia lo más plana posible en la banda de paso . También se lo conoce como filtro de magnitud máximamente plana . Fue descrito por primera vez en 1930 por el ingeniero y físico británico Stephen Butterworth en su artículo titulado "Sobre la teoría de los amplificadores de filtro". ^[1]

Butterworth tenía fama de resolver problemas matemáticos muy complejos que se consideraban "imposibles". En aquella época, el diseño de filtros requería una considerable experiencia en diseño debido a las limitaciones de la teoría que se utilizaba en ese momento . El filtro no se utilizó de forma habitual durante más de 30 años después de su publicación. Butterworth afirmó que:

"Un filtro eléctrico ideal no sólo debería rechazar completamente las frecuencias no deseadas, sino que también debería tener una sensibilidad uniforme para las frecuencias deseadas".

No se puede lograr un filtro ideal de este tipo, pero Butterworth demostró que se obtenían aproximaciones cada vez más cercanas con un número creciente de elementos de filtro de los valores correctos. En ese momento, los filtros generaban una ondulación sustancial en la banda de paso y la elección de los valores de los componentes era altamente interactiva. Butterworth demostró que se podía diseñar un filtro de paso bajo cuya ganancia en función de la frecuencia (es decir, la magnitud de su respuesta de frecuencia ) fuera:

${\displaystyle G(\omega )={\frac {1}{\sqrt {1+{\omega }^{2n}}}},}$

donde es la frecuencia angular en radianes por segundo y es el número de polos en el filtro, igual al número de elementos reactivos en un filtro pasivo. Su frecuencia de corte (el punto de media potencia de aproximadamente −3 dB o una ganancia de voltaje de 1/ √ 2  ≈ 0,7071) se normaliza a 𝜔 = 1 radián por segundo. Butterworth solo trató con filtros con un número par de polos en su artículo, aunque los filtros de orden impar se pueden crear con la adición de un filtro de un solo polo aplicado a la salida del filtro de orden par. Construyó sus filtros de orden superior a partir de filtros de 2 polos separados por amplificadores de tubo de vacío. Su gráfico de la respuesta de frecuencia de filtros de 2, 4, 6, 8 y 10 polos se muestra como A, B, C, D y E en su gráfico original.${\estilo de visualización \omega}$${\estilo de visualización n}$

Butterworth resolvió las ecuaciones para filtros de dos y cuatro polos, mostrando cómo estos últimos podían conectarse en cascada cuando se separaban mediante amplificadores de tubo de vacío , lo que permitía la construcción de filtros de orden superior a pesar de las pérdidas de los inductores . En 1930, no se habían descubierto materiales de núcleo de baja pérdida, como el molypermalloy , y los inductores de audio con núcleo de aire presentaban bastantes pérdidas. Butterworth descubrió que era posible ajustar los valores de los componentes del filtro para compensar la resistencia del bobinado de los inductores.

Utilizó formas de bobinas de 1,25″ de diámetro y 3″ de longitud con terminales enchufables. Los condensadores y resistencias asociados estaban contenidos dentro de la forma de bobina enrollada. La bobina formaba parte de la resistencia de carga de placa. Se utilizaron dos polos por tubo de vacío y se utilizó un acoplamiento RC a la rejilla del siguiente tubo.

Butterworth también demostró que el filtro paso bajo básico podía modificarse para brindar funcionalidad de paso bajo , paso alto , paso de banda y eliminación de banda .

La respuesta de frecuencia del filtro Butterworth es máximamente plana (es decir, no tiene ondulaciones ) en la banda de paso y se reduce hacia cero en la banda de supresión . ^{[2] Cuando se ve en un} diagrama de Bode logarítmico , la respuesta se reduce linealmente hacia el infinito negativo. La respuesta de un filtro de primer orden disminuye a −6 dB por octava (−20 dB por década ) (todos los filtros de paso bajo de primer orden tienen la misma respuesta de frecuencia normalizada). Un filtro de segundo orden disminuye a −12 dB por octava, uno de tercer orden a −18 dB y así sucesivamente. Los filtros Butterworth tienen una función de magnitud que cambia monótonamente con , a diferencia de otros tipos de filtros que tienen una ondulación no monótona en la banda de paso y/o la banda de supresión.${\estilo de visualización \omega}$

En comparación con un filtro Chebyshev Tipo I/Tipo II o un filtro elíptico , el filtro Butterworth tiene una caída más lenta y, por lo tanto, requerirá un orden mayor para implementar una especificación de banda de supresión particular , pero los filtros Butterworth tienen una respuesta de fase más lineal en la banda de paso que la que pueden lograr los filtros Chebyshev Tipo I/Tipo II y los elípticos.

La función de transferencia de un diseño de filtro Butterworth de paso bajo de tercer orden que se muestra en la figura de la derecha se ve así:

${\displaystyle {\frac {V_{o}(s)}{V_{i}(s)}}={\frac {R_{4}}{s^{3}(L_{1}C_{2}L_{3})+s^{2}(L_{1}C_{2}R_{4})+s(L_{1}+L_{3})+R_{4}}}}$

Un ejemplo simple de un filtro Butterworth es el diseño de paso bajo de tercer orden que se muestra en la figura de la derecha, con  = 4/3 F,  = 1 Ω,  = 3/2 H y  = ​​1/2 H. ^[3] Tomando la impedancia de los capacitores como y la impedancia de los inductores como , donde es la frecuencia compleja, las ecuaciones del circuito producen la función de transferencia para este dispositivo:$Estilo de visualización C_{2}$$Estilo de visualización R_{4}$$Estilo de visualización L_{1}$$Estilo de visualización L_{3}$${\estilo de visualización C}$${\displaystyle 1/(Cs)}$${\estilo de visualización L}$${\estilo de visualización Ls}$${\displaystyle s=\sigma+j\omega}$

${\displaystyle H(s)={\frac {V_{o}(s)}{V_{i}(s)}}={\frac {1}{1+2s+2s^{2}+s^{3}}}.}$

La magnitud de la respuesta de frecuencia (ganancia) viene dada por${\displaystyle G(\omega )}$

${\displaystyle G(\omega )=|H(j\omega )|={\frac {1}{\sqrt {1+\omega ^{6}}}},}$

obtenido de

${\displaystyle G^{2}(\omega )=|H(j\omega )|^{2}=H(j\omega )\cdot H^{*}(j\omega )={\frac {1}{1+\omega ^{6}}},}$

y la fase viene dada por

${\displaystyle \Phi (\omega )=\arg(H(j\omega )).\!}$

El retardo de grupo se define como la derivada negativa del cambio de fase con respecto a la frecuencia angular y es una medida de la distorsión en la señal introducida por las diferencias de fase para diferentes frecuencias. La ganancia y el retardo de este filtro se representan en el gráfico de la izquierda. No hay ondulaciones en la curva de ganancia ni en la banda de paso ni en la banda de rechazo.

El logaritmo del valor absoluto de la función de transferencia se representa en el espacio de frecuencias complejo en el segundo gráfico de la derecha. La función está definida por los tres polos en la mitad izquierda del plano de frecuencias complejo.${\displaystyle H(s)}$

Estos están dispuestos en un círculo de radio unitario , simétrico respecto del eje real. La función de ganancia tendrá tres polos más en el semiplano derecho para completar el círculo.${\estilo de visualización s}$

Reemplazando cada inductor por un condensador y cada condensador por un inductor, se obtiene un filtro Butterworth de paso alto.

Un filtro Butterworth de paso de banda se obtiene colocando un condensador en serie con cada inductor y un inductor en paralelo con cada condensador para formar circuitos resonantes. El valor de cada componente nuevo debe seleccionarse para que resuene con el componente antiguo a la frecuencia de interés.

Un filtro Butterworth supresor de banda se obtiene colocando un condensador en paralelo con cada inductor y un inductor en serie con cada condensador para formar circuitos resonantes. El valor de cada componente nuevo debe seleccionarse para que resuene con el componente antiguo a la frecuencia que se desea rechazar.

Como todos los filtros, el prototipo típico es el filtro paso bajo, que puede modificarse para convertirlo en un filtro paso alto o colocarse en serie con otros para formar filtros paso banda y filtro supresor de banda , y versiones de orden superior de estos.

La ganancia de un filtro de paso bajo Butterworth de orden th se da en términos de la función de transferencia como${\displaystyle G(\omega )}$${\estilo de visualización n}$${\displaystyle H(s)}$

${\displaystyle G^{2}(\omega )=\left|H(j\omega )\right|^{2}={\frac {{G_{0}}^{2}}{1+\left({\frac {\omega }{\omega _{c}}}\right)^{2n}}}}$

donde es el orden del filtro, es la frecuencia de corte (aproximadamente la frecuencia de −3 dB), y es la ganancia de CC (ganancia en frecuencia cero).${\displaystyle n}$${\displaystyle \omega _{c}}$${\displaystyle G_{0}}$

Se puede observar que a medida que se acerca al infinito, la ganancia se convierte en una función rectangular y las frecuencias inferiores pasarán con ganancia , mientras que las frecuencias superiores se suprimirán. Para valores más pequeños de , el corte será menos agudo.${\displaystyle n}$${\displaystyle \omega _{c}}$${\displaystyle G_{0}}$${\displaystyle \omega _{c}}$${\displaystyle n}$

Deseamos determinar la función de transferencia donde (a partir de la transformada de Laplace ). Debido a que y , como propiedad general de las transformadas de Laplace en , , si seleccionamos de manera que:${\displaystyle H(s)}$${\displaystyle s=\sigma +j\omega }$${\displaystyle \left|H(s)\right|^{2}=H(s){\overline {H(s)}}}$${\displaystyle s=j\omega }$${\displaystyle H(-j\omega )={\overline {H(j\omega )}}}$${\displaystyle H(s)}$

${\displaystyle H(s)H(-s)={\frac {{G_{0}}^{2}}{1+\left({\frac {-s^{2}}{\omega _{c}^{2}}}\right)^{n}}},}$

Luego, con , tenemos la respuesta de frecuencia del filtro Butterworth.${\displaystyle s=j\omega }$

Los polos de esta expresión se encuentran en un círculo de radio en puntos igualmente espaciados y simétricos alrededor del eje real negativo. Por lo tanto, para lograr estabilidad, la función de transferencia, , se elige de manera que contenga solo los polos en el semiplano real negativo de . El polo -ésimo se especifica mediante${\displaystyle n}$${\displaystyle \omega _{c}}$${\displaystyle H(s)}$${\displaystyle s}$${\displaystyle k}$

${\displaystyle -{\frac {s_{k}^{2}}{\omega _{c}^{2}}}=(-1)^{\frac {1}{n}}=e^{\frac {j(2k-1)\pi }{n}}\qquad k=1,2,3,\ldots ,n}$

y por lo tanto

${\displaystyle s_{k}=\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}\qquad k=1,2,3,\ldots ,n.}$

La función de transferencia (o del sistema) puede escribirse en términos de estos polos como

${\displaystyle H(s)=G_{0}\prod _{k=1}^{n}{\frac {\omega _{c}}{s-s_{k}}}=G_{0}\prod _{k=1}^{n}{\frac {\omega _{c}}{s-\omega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}}}}$.

donde es el producto de un operador de secuencia. El denominador es un polinomio de Butterworth en .${\displaystyle \textstyle {\prod }}$${\displaystyle s}$

Los polinomios de Butterworth pueden escribirse en forma compleja como se indicó anteriormente, pero generalmente se escriben con coeficientes reales multiplicando pares de polos que son conjugados complejos, como y . Los polinomios se normalizan estableciendo . Los polinomios de Butterworth normalizados tienen entonces la forma de producto general${\displaystyle s_{1}}$${\displaystyle s_{n}}$${\displaystyle \omega _{c}=1}$

${\displaystyle B_{n}(s)=\prod _{k=1}^{\frac {n}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]\qquad n={\text{even}}}$

${\displaystyle B_{n}(s)=(s+1)\prod _{k=1}^{\frac {n-1}{2}}\left[s^{2}-2s\cos \left({\frac {2k+n-1}{2n}}\,\pi \right)+1\right]\qquad n={\text{odd}}.}$

Los factores de los polinomios de Butterworth de orden 1 a 10 se muestran en la siguiente tabla (hasta seis decimales).

norte Factores de polinomios de Butterworth${\displaystyle B_{n}(s)}$ 1 ${\displaystyle (s+1)}$ 2 ${\displaystyle (s^{2}+1.414214s+1)}$ 3 ${\displaystyle (s+1)(s^{2}+s+1)}$ 4 ${\displaystyle (s^{2}+0.765367s+1)(s^{2}+1.847759s+1)}$ 5 ${\displaystyle (s+1)(s^{2}+0.618034s+1)(s^{2}+1.618034s+1)}$ 6 ${\displaystyle (s^{2}+0.517638s+1)(s^{2}+1.414214s+1)(s^{2}+1.931852s+1)}$ 7 ${\displaystyle (s+1)(s^{2}+0.445042s+1)(s^{2}+1.246980s+1)(s^{2}+1.801938s+1)}$ 8 ${\displaystyle (s^{2}+0.390181s+1)(s^{2}+1.111140s+1)(s^{2}+1.662939s+1)(s^{2}+1.961571s+1)}$ 9 ${\displaystyle (s+1)(s^{2}+0.347296s+1)(s^{2}+s+1)(s^{2}+1.532089s+1)(s^{2}+1.879385s+1)}$ 10 ${\displaystyle (s^{2}+0.312869s+1)(s^{2}+0.907981s+1)(s^{2}+1.414214s+1)(s^{2}+1.782013s+1)(s^{2}+1.975377s+1)}$

Los factores de los polinomios de Butterworth de orden 1 a 6 se muestran en la siguiente tabla (Exacta).

norte Factores de polinomios de Butterworth${\displaystyle B_{n}(s)}$ 1 ${\displaystyle (s+1)}$ 2 ${\displaystyle (s^{2}+{\sqrt {2}}s+1)}$ 3 ${\displaystyle (s+1)(s^{2}+s+1)}$ 4 ${\displaystyle (s^{2}+{\sqrt {2-{\sqrt {2}}}}s+1)(s^{2}+{\sqrt {2+{\sqrt {2}}}}s+1)}$ 5 ${\displaystyle (s+1)(s^{2}+\varphi ^{-1}s+1)(s^{2}+\varphi s+1)}$ 6 ${\displaystyle (s^{2}+{\sqrt {2-{\sqrt {3}}}}s+1)(s^{2}+{\sqrt {2}}s+1)(s^{2}+{\sqrt {2+{\sqrt {3}}}}s+1)}$

donde la letra griega phi ( o ) representa la proporción áurea . Es un número irracional que es una solución a la ecuación cuadrática con un valor de ^{[4] [5]}${\displaystyle \varphi }$${\displaystyle \phi }$ ${\displaystyle x^{2}-x-1=0,}$

${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}=1.618033988749...}$( OEIS : A001622 )

El polinomio de Butterworth enésimo también se puede escribir como suma${\displaystyle n}$

${\displaystyle B_{n}(s)=\sum _{k=0}^{n}a_{k}s^{k}\,,}$

con sus coeficientes dados por la fórmula de recursión ^{[6] [7]}${\displaystyle a_{k}}$

${\displaystyle {\frac {a_{k+1}}{a_{k}}}={\frac {\cos(k\gamma )}{\sin((k+1)\gamma )}}}$

y por la fórmula del producto

${\displaystyle a_{k}=\prod _{\mu =1}^{k}{\frac {\cos((\mu -1)\gamma )}{\sin(\mu \gamma )}}\,,}$

dónde

${\displaystyle a_{0}=1\qquad {\text{and}}\qquad \gamma ={\frac {\pi }{2n}}\,.}$

Además , los coeficientes redondeados para los primeros 10 polinomios de Butterworth son:${\displaystyle a_{k}=a_{n-k}}$${\displaystyle a_{k}}$${\displaystyle B_{n}(s)}$

Coeficientes de Butterworth con cuatro decimales${\displaystyle a_{k}}$

${\displaystyle n}$	${\displaystyle a_{0}}$	${\displaystyle a_{1}}$	${\displaystyle a_{2}}$	${\displaystyle a_{3}}$	${\displaystyle a_{4}}$	${\displaystyle a_{5}}$	${\displaystyle a_{6}}$	${\displaystyle a_{7}}$	${\displaystyle a_{8}}$	${\displaystyle a_{9}}$	${\displaystyle a_{10}}$
${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 1}$
${\displaystyle 2}$	${\displaystyle 1}$	${\displaystyle 1.4142}$	${\displaystyle 1}$
${\displaystyle 3}$	${\displaystyle 1}$	${\displaystyle 2}$	${\displaystyle 2}$	${\displaystyle 1}$
${\displaystyle 4}$	${\displaystyle 1}$	${\displaystyle 2.6131}$	${\displaystyle 3.4142}$	${\displaystyle 2.6131}$	${\displaystyle 1}$
${\displaystyle 5}$	${\displaystyle 1}$	${\displaystyle 3.2361}$	${\displaystyle 5.2361}$	${\displaystyle 5.2361}$	${\displaystyle 3.2361}$	${\displaystyle 1}$
${\displaystyle 6}$	${\displaystyle 1}$	${\displaystyle 3.8637}$	${\displaystyle 7.4641}$	${\displaystyle 9.1416}$	${\displaystyle 7.4641}$	${\displaystyle 3.8637}$	${\displaystyle 1}$
${\displaystyle 7}$	${\displaystyle 1}$	${\displaystyle 4.4940}$	${\displaystyle 10.0978}$	${\displaystyle 14.5918}$	${\displaystyle 14.5918}$	${\displaystyle 10.0978}$	${\displaystyle 4.4940}$	${\displaystyle 1}$
${\displaystyle 8}$	${\displaystyle 1}$	${\displaystyle 5.1258}$	${\displaystyle 13.1371}$	${\displaystyle 21.8462}$	${\displaystyle 25.6884}$	${\displaystyle 21.8462}$	${\displaystyle 13.1371}$	${\displaystyle 5.1258}$	${\displaystyle 1}$
${\displaystyle 9}$	${\displaystyle 1}$	${\displaystyle 5.7588}$	${\displaystyle 16.5817}$	${\displaystyle 31.1634}$	${\displaystyle 41.9864}$	${\displaystyle 41.9864}$	${\displaystyle 31.1634}$	${\displaystyle 16.5817}$	${\displaystyle 5.7588}$	${\displaystyle 1}$
${\displaystyle 10}$	${\displaystyle 1}$	${\displaystyle 6.3925}$	${\displaystyle 20.4317}$	${\displaystyle 42.8021}$	${\displaystyle 64.8824}$	${\displaystyle 74.2334}$	${\displaystyle 64.8824}$	${\displaystyle 42.8021}$	${\displaystyle 20.4317}$	${\displaystyle 6.3925}$	${\displaystyle 1}$

Los polinomios de Butterworth normalizados se pueden utilizar para determinar la función de transferencia para cualquier frecuencia de corte de filtro de paso bajo , de la siguiente manera${\displaystyle \omega _{c}}$

${\displaystyle H(s)={\frac {G_{0}}{B_{n}(a)}}}$, dónde${\displaystyle a={\frac {s}{\omega _{c}}}.}$

También es posible la transformación a otras formas de banda, consulte filtro prototipo .

Suponiendo y , se puede demostrar que la derivada de la ganancia con respecto a la frecuencia es${\displaystyle \omega _{c}=1}$${\displaystyle G_{0}=1}$

${\displaystyle {\frac {dG}{d\omega }}=-nG^{3}\omega ^{2n-1}}$

que es monótonamente decreciente para todos, ya que la ganancia siempre es positiva. Por lo tanto, la función de ganancia del filtro Butterworth no tiene ondulación. La expansión en serie de la ganancia está dada por${\displaystyle \omega }$${\displaystyle G}$

${\displaystyle G(\omega )=1-{\frac {1}{2}}\omega ^{2n}+{\frac {3}{8}}\omega ^{4n}+\ldots }$

En otras palabras, todas las derivadas de la ganancia hasta la derivada 2 -ésima pero no incluida son cero en , lo que da como resultado una "planitud máxima". Si el requisito de ser monótono se limita solo a la banda de paso y se permiten ondulaciones en la banda de rechazo, entonces es posible diseñar un filtro del mismo orden, como el filtro Chebyshev inverso , que sea más plano en la banda de paso que el Butterworth "máximamente plano".${\displaystyle n}$${\displaystyle \omega =0}$

Suponiendo nuevamente que la pendiente del logaritmo de la ganancia para grande es${\displaystyle \omega _{c}=1}$${\displaystyle \omega }$

${\displaystyle \lim _{\omega \rightarrow \infty }{\frac {d\log(G)}{d\log(\omega )}}=-n.}$

En decibeles , la reducción de alta frecuencia es, por lo tanto, de 20  dB/década, o 6  dB/octava (se utiliza el factor 20 porque la potencia es proporcional al cuadrado de la ganancia de voltaje; consulte la regla del logaritmo de 20 ).${\displaystyle n}$${\displaystyle n}$

Para diseñar un filtro Butterworth utilizando el número mínimo requerido de elementos, el orden mínimo del filtro Butterworth se puede calcular de la siguiente manera. ^[8]

${\displaystyle n=\left\lceil {\frac {\log {{\bigr (}{\frac {10^{\alpha _{s}/10}-1}{10^{\alpha _{p}/10}-1}}}{\bigr )}}{2\log {(\omega _{s}/\omega _{p})}}}\right\rceil }$

dónde:

${\displaystyle \omega _{p}}$y son la frecuencia de la banda de paso y la atenuación en esa frecuencia en dB.${\displaystyle \alpha _{p}}$

${\displaystyle \omega _{s}}$y son la frecuencia de la banda de parada y la atenuación en esa frecuencia en dB.${\displaystyle \alpha _{s}}$

${\displaystyle n}$es el número mínimo de polos, el orden del filtro.

${\displaystyle \lceil \cdot \rceil }$denota la función de techo .

La atenuación de corte para los filtros Butterworth se define generalmente como -3,01 dB. Si se desea utilizar una atenuación diferente en la frecuencia de corte, se puede aplicar el siguiente factor a cada polo, con lo que los polos seguirán estando sobre un círculo, pero el radio ya no será la unidad. ^[8] La ecuación de atenuación de corte se puede derivar mediante la manipulación algebraica de la ecuación de definición de Butterworth que se indica en la parte superior de la página. ^[9]

$${\displaystyle {\begin{aligned}p_{A}=p_{1}\times (10^{\alpha /10}-1)^{{-1}/{2n}}&\qquad {\text{For 0}}\leq \alpha <\infty \end{aligned}}}$$

dónde:

${\displaystyle p_{A}}$es el polo reubicado posicionado para establecer la atenuación de corte deseada.

${\displaystyle p_{1}}$es un polo de corte de -3,01 dB que se encuentra en el círculo unitario.

${\displaystyle \alpha }$es la atenuación deseada en la frecuencia de corte en dB (1 dB, 10 dB, etc.).

${\displaystyle n}$es el número de polos, el orden del filtro.

Existen varias topologías de filtro diferentes disponibles para implementar un filtro analógico lineal. La topología más utilizada para una realización pasiva es la topología Cauer, y la topología más utilizada para una realización activa es la topología Sallen–Key.

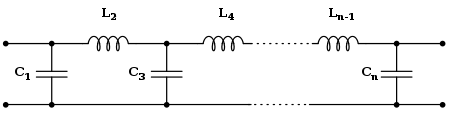
La topología de Cauer utiliza componentes pasivos (condensadores en derivación e inductores en serie) para implementar un filtro analógico lineal. El filtro Butterworth con una función de transferencia determinada se puede implementar utilizando una forma Cauer 1. El elemento k -ésimo se da por ^[10]

${\displaystyle C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k={\text{odd}}}$

${\displaystyle L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k={\text{even}}.}$

Si se desea, el filtro puede comenzar con un inductor en serie, en cuyo caso los valores L _k son k impares y los valores C _k son k pares. Estas fórmulas pueden combinarse de manera útil haciendo que tanto L _k como C _k sean iguales a g _k . Es decir, g _k es la inmitancia dividida por s .

${\displaystyle g_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k=1,2,3,\ldots ,n.}$

Estas fórmulas se aplican a un filtro de doble terminación (es decir, la impedancia de la fuente y de la carga son iguales a la unidad) con ω _c = 1. Este filtro prototipo se puede escalar para otros valores de impedancia y frecuencia. Para un filtro de terminación simple (es decir, uno accionado por una fuente de voltaje o corriente ideal), los valores de los elementos se dan por ^[3]

${\displaystyle g_{j}={\frac {a_{j}a_{j-1}}{c_{j-1}g_{j-1}}}\qquad j=2,3,\ldots ,n}$

dónde

${\displaystyle g_{1}=a_{1}}$

y

${\displaystyle a_{j}=\sin \left[{\frac {(2j-1)}{2n}}\pi \right]\qquad j=1,2,3,\ldots ,n}$

${\displaystyle c_{j}=\cos ^{2}\left[{\frac {j}{2n}}\pi \right]\qquad j=1,2,3,\ldots ,n.}$

Los filtros accionados por tensión deben comenzar con un elemento en serie y los filtros accionados por corriente deben comenzar con un elemento en derivación. Estas formas son útiles en el diseño de diplexores y multiplexores . ^[3]

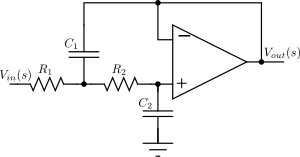
La topología Sallen-Key utiliza componentes activos y pasivos (buffers no inversores, generalmente amplificadores operacionales , resistencias y capacitores) para implementar un filtro analógico lineal. Cada etapa Sallen-Key implementa un par conjugado de polos; el filtro general se implementa conectando en cascada todas las etapas en serie. Si hay un polo real (en el caso en el que sea impar), este debe implementarse por separado, generalmente como un circuito RC , y conectarse en cascada con las etapas activas.${\displaystyle n}$

Para el circuito Sallen-Key de segundo orden que se muestra a la derecha, la función de transferencia está dada por

${\displaystyle H(s)={\frac {V_{\text{out}}(s)}{V_{\text{in}}(s)}}={\frac {1}{1+C_{2}(R_{1}+R_{2})s+C_{1}C_{2}R_{1}R_{2}s^{2}}}.}$

Deseamos que el denominador sea uno de los términos cuadráticos de un polinomio de Butterworth. Suponiendo que , esto significará que${\displaystyle \omega _{c}=1}$

${\displaystyle C_{1}C_{2}R_{1}R_{2}=1\,}$

y

${\displaystyle C_{2}(R_{1}+R_{2})=-2\cos \left({\frac {2k+n-1}{2n}}\pi \right).}$

Esto deja dos valores de componentes indefinidos que pueden elegirse a voluntad.

Huelsman ^{[11] [12]} describe filtros Butterworth de paso bajo con topología Sallen–Key de tercer y cuarto orden, utilizando solo un amplificador operacional , y Jurišić et al. ^[13] describen otros filtros Butterworth de un solo amplificador también de orden superior.

Las implementaciones digitales de Butterworth y otros filtros a menudo se basan en el método de transformación bilineal o el método de transformación Z adaptada , dos métodos diferentes para discretizar un diseño de filtro analógico. En el caso de filtros de todos los polos como el Butterworth, el método de transformación Z adaptada es equivalente al método de invariancia de impulso . Para órdenes superiores, los filtros digitales son sensibles a errores de cuantificación, por lo que a menudo se calculan como secciones bicuadradas en cascada , más una sección de primer o tercer orden para órdenes impares.

Las propiedades del filtro Butterworth son:

• Respuesta de amplitud monótona tanto en banda de paso como en banda de supresión
• Caída rápida alrededor de la frecuencia de corte, que mejora a medida que aumenta el orden.
• Sobreimpulso considerable y zumbido en la respuesta al escalón , que empeora al aumentar el orden
• Respuesta de fase ligeramente no lineal
• El retraso del grupo depende en gran medida de la frecuencia

Aquí se muestra una imagen que muestra la ganancia de un filtro Butterworth de tiempo discreto junto a otros tipos de filtros comunes. Todos estos filtros son de quinto orden.

El filtro Butterworth disminuye más lentamente alrededor de la frecuencia de corte que el filtro Chebyshev o el filtro elíptico , pero sin ondulación.

• Filtro de Bessel
• Filtro de Chebyshev
• Filtro de peine
• Filtro elíptico
• Diseño de filtros