Circuito RC

Este artículo necesita citas adicionales para su verificación . Por favor, ayude a mejorar este artículo añadiendo citas de fuentes fiables . El material sin fuentes puede ser cuestionado y eliminado. Buscar fuentes:  «RC circuit» – noticias  · periódicos  · libros  · académico  · JSTOR ( marzo de 2018 ) ( Aprenda cómo y cuándo eliminar este mensaje )

Un circuito de resistencia-capacitor ( circuito RC ), o filtro RC o red RC , es un circuito eléctrico compuesto de resistencias y capacitores . Puede ser accionado por una fuente de voltaje o corriente y estas producirán diferentes respuestas. Un circuito RC de primer orden está compuesto por una resistencia y un capacitor y es el tipo más simple de circuito RC.

Los circuitos RC se pueden utilizar para filtrar una señal bloqueando ciertas frecuencias y dejando pasar otras. Los dos filtros RC más comunes son los filtros de paso alto y los filtros de paso bajo ; los filtros de paso de banda y los filtros de eliminación de banda generalmente requieren filtros RLC , aunque se pueden hacer algunos rudimentarios con filtros RC.

Hay tres componentes básicos de un circuito analógico pasivo lineal concentrado : la resistencia (R), el condensador (C) y el inductor (L). Estos pueden combinarse en el circuito RC, el circuito RL , el circuito LC y el circuito RLC , con las siglas que indican qué componentes se utilizan. Estos circuitos, entre ellos, exhiben una gran cantidad de tipos importantes de comportamiento que son fundamentales para gran parte de la electrónica analógica . En particular, pueden actuar como filtros pasivos . Este artículo considera el circuito RC, tanto en forma de serie como de paralelo , como se muestra en los diagramas a continuación.

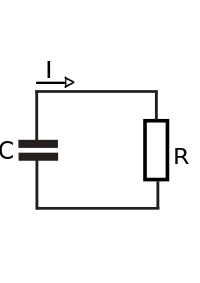
El circuito RC más simple consiste en una resistencia y un condensador cargado conectados entre sí en un solo bucle, sin una fuente de voltaje externa. Una vez que el circuito está cerrado, el condensador comienza a descargar su energía almacenada a través de la resistencia. El voltaje a través del condensador, que depende del tiempo, se puede encontrar utilizando la ley de corriente de Kirchhoff . La corriente a través de la resistencia debe ser igual en magnitud (pero opuesta en signo) a la derivada temporal de la carga acumulada en el condensador. Esto da como resultado la ecuación diferencial lineal

${\displaystyle C{\frac {dV}{dt}}+{\frac {V}{R}}=0\,,}$

donde C es la capacitancia del capacitor.

Resolviendo esta ecuación para V se obtiene la fórmula para la desintegración exponencial :

${\displaystyle V(t)=V_{0}e^{-{\frac {t}{RC}}}\,,}$

donde V ₀ es el voltaje del capacitor en el tiempo t = 0 .

El tiempo necesario para que el voltaje caiga a ⁠V ₀/mi⁠ se llama constante de tiempo RC y se expresa por, ^[1]

${\displaystyle \tau=RC\,.}$

En esta fórmula, τ se mide en segundos, R en ohmios y C en faradios.

La impedancia compleja , Z _C (en ohmios ) de un capacitor con capacitancia C (en faradios ) es

${\displaystyle Z_{C}={\frac {1}{sC}}}$

La frecuencia compleja s es, en general, un número complejo ,

${\displaystyle s=\sigma+j\omega \,,}$

dónde

• j representa la unidad imaginaria : j ² = −1 ,
• σ es la constante de decaimiento exponencial (en nepers por segundo), y
• ω es la frecuencia angular sinusoidal (en radianes por segundo ).

El estado estable sinusoidal es un caso especial en el que el voltaje de entrada consiste en una sinusoide pura (sin decaimiento exponencial). Como resultado, la impedancia se vuelve${\displaystyle \sigma = 0}$

${\displaystyle Z_{C}={\frac {1}{j\omega C}}=-{\frac {j}{\omega C}}\,.}$

Al considerar el circuito como un divisor de voltaje , el voltaje a través del capacitor es:

${\displaystyle V_{C}(s)={\frac {\frac {1}{Cs}}{R+{\frac {1}{Cs}}}V_{\mathrm {en} }(s)={\frac {1}{1+RCs}}V_{\mathrm {en} }(s)}$

y el voltaje a través de la resistencia es:

${\displaystyle V_{R}(s)={\frac {R}{R+{\frac {1}{Cs}}}}V_{\mathrm {en} }(s)={\frac {RCs}{1+RCs}}V_{\mathrm {en} }(s)\,.}$

La función de transferencia del voltaje de entrada al voltaje a través del capacitor es

${\displaystyle H_{C}(s)={\frac {V_{C}(s)}{V_{\mathrm {en} }(s)}}={\frac {1}{1+RCs}}\,.}$

De manera similar, la función de transferencia desde la entrada al voltaje a través de la resistencia es

${\displaystyle H_{R}(s)={\frac {V_{R}(s)}{V_{\rm {en}}(s)}}={\frac {RCs}{1+RCs}}\,.}$

Ambas funciones de transferencia tienen un solo polo ubicado en

${\displaystyle s=-{\frac {1}{RC}}\,.}$

Además, la función de transferencia del voltaje a través de la resistencia tiene un cero ubicado en el origen .

La magnitud de las ganancias en los dos componentes es

${\displaystyle G_{C}={\big |}H_{C}(j\omega ){\big |}=\left|{\frac {V_{C}(j\omega )}{V_{\mathrm {in} }(j\omega )}}\right|={\frac {1}{\sqrt {1+\left(\omega RC\right)^{2}}}}}$

y

${\displaystyle G_{R}={\big |}H_{R}(j\omega ){\big |}=\left|{\frac {V_{R}(j\omega )}{V_{\mathrm {in} }(j\omega )}}\right|={\frac {\omega RC}{\sqrt {1+\left(\omega RC\right)^{2}}}}\,,}$

y los ángulos de fase son

${\displaystyle \phi _{C}=\angle H_{C}(j\omega )=\tan ^{-1}\left(-\omega RC\right)}$

y

${\displaystyle \phi _{R}=\angle H_{R}(j\omega )=\tan ^{-1}\left({\frac {1}{\omega RC}}\right)\,.}$

Estas expresiones juntas pueden sustituirse en la expresión habitual para el fasor que representa la salida:

${\displaystyle {\begin{aligned}V_{C}&=G_{C}V_{\mathrm {in} }e^{j\phi _{C}}\\V_{R}&=G_{R}V_{\mathrm {in} }e^{j\phi _{R}}\,.\end{aligned}}}$

La corriente en el circuito es la misma en todas partes ya que el circuito está en serie:

${\displaystyle I(s)={\frac {V_{\mathrm {in} }(s)}{R+{\frac {1}{Cs}}}}={\frac {Cs}{1+RCs}}V_{\mathrm {in} }(s)\,.}$

La respuesta al impulso para cada voltaje es la transformada de Laplace inversa de la función de transferencia correspondiente. Representa la respuesta del circuito a un voltaje de entrada que consiste en un impulso o función delta de Dirac .

La respuesta al impulso para el voltaje del capacitor es

${\displaystyle h_{C}(t)={\frac {1}{RC}}e^{-{\frac {t}{RC}}}u(t)={\frac {1}{\tau }}e^{-{\frac {t}{\tau }}}u(t)\,,}$

donde u ( t ) es la función escalón de Heaviside y τ = RC es la constante de tiempo .

De manera similar, la respuesta al impulso para el voltaje de la resistencia es

${\displaystyle h_{R}(t)=\delta (t)-{\frac {1}{RC}}e^{-{\frac {t}{RC}}}u(t)=\delta (t)-{\frac {1}{\tau }}e^{-{\frac {t}{\tau }}}u(t)\,,}$

donde δ ( t ) es la función delta de Dirac

Se trata de expresiones del dominio de la frecuencia . Su análisis mostrará qué frecuencias pasan y rechazan los circuitos (o filtros). Este análisis se basa en la consideración de lo que sucede con estas ganancias a medida que la frecuencia se vuelve muy grande o muy pequeña.

Como ω → ∞ :

${\displaystyle G_{C}\to 0\quad {\mbox{and}}\quad G_{R}\to 1\,.}$

Como ω → 0 :

${\displaystyle G_{C}\to 1\quad {\mbox{and}}\quad G_{R}\to 0\,.}$

Esto demuestra que, si la salida se toma a través del condensador, las frecuencias altas se atenúan (se ponen en cortocircuito a tierra) y las frecuencias bajas pasan. Por lo tanto, el circuito se comporta como un filtro de paso bajo . Sin embargo, si la salida se toma a través de la resistencia, las frecuencias altas pasan y las frecuencias bajas se atenúan (ya que el condensador bloquea la señal cuando su frecuencia se acerca a 0). En esta configuración, el circuito se comporta como un filtro de paso alto .

El rango de frecuencias por las que pasa el filtro se denomina ancho de banda . El punto en el que el filtro atenúa la señal a la mitad de su potencia sin filtrar se denomina frecuencia de corte . Esto requiere que la ganancia del circuito se reduzca a

${\displaystyle G_{C}=G_{R}={\frac {1}{\sqrt {2}}}}$.

Resolviendo la ecuación anterior obtenemos

${\displaystyle \omega _{\mathrm {c} }={\frac {1}{RC}}\quad {\mbox{or}}\quad f_{\mathrm {c} }={\frac {1}{2\pi RC}}}$

que es la frecuencia que el filtro atenuará a la mitad de su potencia original.

Claramente, las fases también dependen de la frecuencia, aunque este efecto es menos interesante en general que las variaciones de ganancia.

Como ω → 0 :

${\displaystyle \phi _{C}\to 0\quad {\mbox{and}}\quad \phi _{R}\to 90^{\circ }={\frac {\pi }{2}}{\mbox{ radians}}\,.}$

Como ω → ∞ :

${\displaystyle \phi _{C}\to -90^{\circ }=-{\frac {\pi }{2}}{\mbox{ radians}}\quad {\mbox{and}}\quad \phi _{R}\to 0\,.}$

Por lo tanto, en CC (0  Hz ), el voltaje del capacitor está en fase con el voltaje de la señal, mientras que el voltaje de la resistencia se adelanta 90°. A medida que aumenta la frecuencia, el voltaje del capacitor llega a tener un desfase de 90° con respecto a la señal y el voltaje de la resistencia llega a estar en fase con la señal.

Esta sección se basa en el conocimiento de e , la constante logarítmica natural .

La forma más directa de derivar el comportamiento en el dominio del tiempo es utilizar las transformadas de Laplace de las expresiones para V _C y V _R dadas anteriormente. Esto transforma efectivamente jω → s . Suponiendo una entrada escalonada (es decir, V _in = 0 antes de t = 0 y luego V _in = V después):

${\displaystyle {\begin{aligned}V_{\mathrm {in} }(s)&=V\cdot {\frac {1}{s}}\\V_{C}(s)&=V\cdot {\frac {1}{1+sRC}}\cdot {\frac {1}{s}}\\V_{R}(s)&=V\cdot {\frac {sRC}{1+sRC}}\cdot {\frac {1}{s}}\,.\end{aligned}}}$

Las expansiones de fracciones parciales y la transformada inversa de Laplace dan como resultado:

${\displaystyle {\begin{aligned}V_{C}(t)&=V\left(1-e^{-{\frac {t}{RC}}}\right)\\V_{R}(t)&=Ve^{-{\frac {t}{RC}}}\,.\end{aligned}}}$

Estas ecuaciones sirven para calcular el voltaje a través del capacitor y la resistencia respectivamente mientras el capacitor se está cargando ; para la descarga, las ecuaciones son al revés. Estas ecuaciones se pueden reescribir en términos de carga y corriente utilizando las relaciones C = ⁠Q/V⁠ y V = IR (verley de Ohm).

Por lo tanto, el voltaje a través del capacitor tiende hacia V a medida que pasa el tiempo, mientras que el voltaje a través del resistor tiende hacia 0, como se muestra en las figuras. Esto está en consonancia con el punto intuitivo de que el capacitor se cargará a partir del voltaje de suministro a medida que pasa el tiempo y, finalmente, se cargará por completo.

Estas ecuaciones muestran que un circuito RC en serie tiene una constante de tiempo , generalmente denotada τ = RC, que es el tiempo que tarda el voltaje a través del componente en aumentar (a través del capacitor) o disminuir (a través de la resistencia) dentro de ⁠1/mi⁠ de su valor final. Es decir, τ es el tiempo que tarda V _C en alcanzar V (1 − ⁠1/mi⁠ ) ​​y V _R para alcanzar V ( ⁠1/mi⁠ ) ​​.

La tasa de cambio es una fracción de 1 − ⁠1/mi⁠ por τ . Por lo tanto, al pasar de t = Nτ a t = ( N + 1) τ , el voltaje se habrá movido aproximadamente el 63,2% del camino desde su nivel en t = Nτ hacia su valor final. Por lo tanto, el condensador se cargará a aproximadamente el 63,2% después de τ , y esencialmente completamente cargado (99,3%) después de aproximadamente 5 τ . Cuando la fuente de voltaje se reemplaza con un cortocircuito, con el condensador completamente cargado, el voltaje a través del condensador cae exponencialmente con t desde V hacia 0. El condensador se descargará a aproximadamente el 36,8% después de τ , y esencialmente completamente descargado (0,7%) después de aproximadamente 5 τ . Tenga en cuenta que la corriente, I , en el circuito se comporta como lo hace el voltaje a través del resistor, a través de la Ley de Ohm .

Estos resultados también pueden obtenerse resolviendo las ecuaciones diferenciales que describen el circuito:

${\displaystyle {\begin{aligned}{\frac {V_{\mathrm {in} }-V_{C}}{R}}&=C{\frac {dV_{C}}{dt}}\\V_{R}&=V_{\mathrm {in} }-V_{C}\,.\end{aligned}}}$

La primera ecuación se resuelve utilizando un factor de integración y la segunda se deduce fácilmente; las soluciones son exactamente las mismas que las obtenidas mediante las transformadas de Laplace.

Considere la salida a través del capacitor a alta frecuencia, es decir

${\displaystyle \omega \gg {\frac {1}{RC}}\,.}$

Esto significa que el condensador no tiene tiempo suficiente para cargarse y, por lo tanto, su voltaje es muy pequeño. Por lo tanto, el voltaje de entrada es aproximadamente igual al voltaje a través del resistor. Para comprobarlo, considere la expresión dada anteriormente:${\displaystyle I}$

${\displaystyle I={\frac {V_{\mathrm {in} }}{R+{\frac {1}{j\omega C}}}}\,,}$

pero tenga en cuenta que la condición de frecuencia descrita significa que

${\displaystyle \omega C\gg {\frac {1}{R}}\,,}$

entonces

${\displaystyle I\approx {\frac {V_{\mathrm {in} }}{R}}}$

que es simplemente la Ley de Ohm .

Ahora,

${\displaystyle V_{C}={\frac {1}{C}}\int _{0}^{t}I\,dt\,,}$

entonces

${\displaystyle V_{C}\approx {\frac {1}{RC}}\int _{0}^{t}V_{\mathrm {in} }\,dt\,,}$

que es un integrador a través del capacitor .

Considere la salida a través de la resistencia a baja frecuencia, es decir,

${\displaystyle \omega \ll {\frac {1}{RC}}\,.}$

Esto significa que el capacitor tiene tiempo de cargarse hasta que su voltaje sea casi igual al voltaje de la fuente. Considerando nuevamente la expresión para I , cuando

${\displaystyle R\ll {\frac {1}{\omega C}}\,,}$

entonces

${\displaystyle {\begin{aligned}I&\approx {\frac {V_{\mathrm {in} }}{\frac {1}{j\omega C}}}\\V_{\mathrm {in} }&\approx {\frac {I}{j\omega C}}=V_{C}\,.\end{aligned}}}$

Ahora,

${\displaystyle {\begin{aligned}V_{R}&=IR=C{\frac {dV_{C}}{dt}}R\\V_{R}&\approx RC{\frac {dV_{in}}{dt}}\,,\end{aligned}}}$

que es un diferenciador a través de la resistencia .

La integración y la diferenciación también se pueden lograr colocando resistencias y capacitores según sea apropiado en la entrada y el bucle de retroalimentación de los amplificadores operacionales (ver integrador de amplificador operacional y diferenciador de amplificador operacional ).

El circuito RC en paralelo generalmente es menos interesante que el circuito en serie. Esto se debe principalmente a que el voltaje de salida _Vout es igual al voltaje de entrada Vin _; como resultado, este circuito no actúa como un filtro en la señal de entrada a menos que sea alimentada por una fuente de corriente .

Con impedancias complejas:

${\displaystyle {\begin{aligned}I_{R}&={\frac {V_{\mathrm {in} }}{R}}\\I_{C}&=j\omega CV_{\mathrm {in} }\,.\end{aligned}}}$

Esto demuestra que la corriente del capacitor está desfasada 90° con respecto a la corriente del resistor (y de la fuente). Alternativamente, se pueden utilizar las ecuaciones diferenciales que rigen el problema:

${\displaystyle {\begin{aligned}I_{R}&={\frac {V_{\mathrm {in} }}{R}}\\I_{C}&=C{\frac {dV_{\mathrm {in} }}{dt}}\,.\end{aligned}}}$

Cuando se alimenta mediante una fuente de corriente, la función de transferencia de un circuito RC paralelo es:

${\displaystyle {\frac {V_{\mathrm {out} }}{I_{\mathrm {in} }}}={\frac {R}{1+sRC}}\,.}$

A veces es necesario sintetizar un circuito RC a partir de una función racional dada en s . Para que la síntesis sea posible en elementos pasivos, la función debe ser una función real positiva . Para sintetizar como un circuito RC, todas las frecuencias críticas ( polos y ceros ) deben estar en el eje real negativo y alternar entre polos y ceros con un número igual de cada uno. Además, la frecuencia crítica más cercana al origen debe ser un polo, suponiendo que la función racional representa una impedancia en lugar de una admitancia.

La síntesis se puede lograr con una modificación de la síntesis de Foster o la síntesis de Cauer que se utilizan para sintetizar circuitos LC . En el caso de la síntesis de Cauer, se obtendrá una red en escalera de resistencias y condensadores. ^[2]

• Constante de tiempo RC
• Circuito RL
• Circuito LC
• Circuito RLC
• Red eléctrica
• Lista de temas de electrónica
• Respuesta escalonada

• Bakshi, UA; Bakshi, AV, Análisis de circuitos - II , Publicaciones técnicas, 2009 ISBN  9788184315974 .
• Horowitz, Paul; Hill, Winfield, El arte de la electrónica (3.ª edición), Cambridge University Press, 2015 ISBN 0521809266 .